| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 设计艺术 -> 大模型微调到底有没有技术含量,或者说技术含量到底有多大? -> 正文阅读 |
|
|
[设计艺术]大模型微调到底有没有技术含量,或者说技术含量到底有多大? |
| [收藏本文] 【下载本文】 |
|
大模型微调到底有没有技术含量,或者说技术含量到底有多大? 关注问题?写回答 [img_log] 神经网络 深度学习(Deep Learning) GPT-4 ChatGPT 多模态大模型 大模型微调到底有没有技术含量,或者说技术含量到底有多大? |
|
老生常谈的一句话吧:有没有技术含量取决于这个工作你怎么做,尤其是 llm 方向,上手门槛相比传统 NLP 变得更低了。 我举一些例子吧,针对大模型微调的几个重要环节,我列举的每一种做法大概率都能完成最终目标,甚至说训出来的模型效果都没什么差别。但对个人能力成长的帮助就大不相同了。 数据工作 做法 1 : 继承实验室或者同事的训练数据,拿到之后也不 check 一下数据质量,直接放进去训。 做法 2 : 下载一个开源数据,构建“system + query + answer”集合。 做法 3 : 利用 gpt4 生成数据,学会用 gpt4 喜好的 prompt 去请求。并且意识到数据 prompt 多样性,想尽各种办法去扩充 prompt 的任务多样性和表达方式多样性,甚至去刻意加一些 noisy prompt 去提升抗噪性。同时,愿意放下身架,一条一条去 check 数据质量,去和标注同学对齐标注标准。 做法 4 : 利用用户的交互日志来驱动数据构造过程,收集用户的真实 prompt,用规则或者GPT4去分析用户的 feedback,进而获得高质量的 answer 数据。 做法 5 : 借鉴 cot、rag、 function_call、agent 等思路,把复杂的模型无法胜任的任务在数据层面就进行拆解,比如“模型写不出长篇小说” --> “模型写小说大纲,模型基于小说大纲写长篇小说”。 …… 训练代码 做法 1 : 继承实验室或者同事的训练代码,修改 data_path,然后 bash train.sh。 做法 2 : 继承或自己下载一份训练代码,研究启动代码的每一个参数,去寻思并去搞懂:为啥开 offload,什么叫 sequence_parallel,等等。然后再去看看 dataloader 是怎么处理数据格式,session 数据的 loss 是只计算最后一轮还是每轮都算,代码中应用了哪些 special_token 等等。 做法 3 : 不仅搞懂了每个参数,还提出自己的见解:epoch = 3 是不是太多了,10W 条训练数据这个量级合适吗?special_token 是不是引入的太多了?7B 模型用这个学习率是不是太大了,warmup 该用多少 step 或者说能不能不开 warmup?带着疑惑然后去问问 chatgpt 老师怎么说,或者搜搜大佬们的文章拜读一下。 做法 4 : 质疑和改进训练代码,deepspeed 是不是有点慢,要不要改成 megatron 框架?把 megatron 和 deepspeed 的优点结合起来?如果有兴趣,也可以去 debug 下速度, 发现 rope 的耗时会比 attention 都长的时候想想办法去优化(查查大佬们的优化方案)? …… 实验分析 做法 1 : 跑事前准备好的评估集,然后自评或送评,正向收益的话这个工作纠结束了,负向收益的话就认为是数据不干净,想办法去清洗数据或者是构造更多的训练数据,哪个 task 的指标差就重点优化这个 task 的训练数据。 做法 2 : 结合 pretrain 模型 / sft_base 模型的结果,去归类和分析每一个 sft_exp 模型的 bad case,归类分析:幻觉问题?pattern 过拟合问题?问题太难训练不充分问题?pretrain模型压根就没有这个能力?这个 size 的模型就做不了这种复杂逻辑问题?…… 针对自己的分析结果,设计实验去验证。怀疑某个 task 欠拟合,就上采样这个 task 的数据;怀疑是训过拟合了,就抽一些训练数据的 prompt 格式,让模型去回答类似的问题;不知道 7B 模型能不能解决好这个任务,就去下载 llama、qwen、mistral、deepspeek 等同 size 的 chat 模型去验证效果;等等等等。 这个过程要往往要积攒一些经验,学会一些小 trick: 让 pretrain 模型去续写,来判断某个能力或某个知识是模型压根没有,还是说被自己训没了;观察某个 token 的概率;观察模型在第几个 token 开始回答错误的;如果模型的 pattern 输出错误,比如没有按照 json 输出,看一下是不会 json,还是不知道该出 json,可以把``json```也喂给模型,看模型的续写情况;模型把“日本的首都回答成了北京“了,不要直接断言是幻觉,而是分析下模型是对“日本””首都“”北京“哪个 token 过拟合了,有可能是模型把所有国家的首都都回答成北京,也有可能模型是把日本的任何城市都回答成北京。进而看下训练集和这个 pattern 有关的语料是不是太多了;…… 做法 3 : 不仅意识到模型结果和数据质量有关,还去分析和训练方法的关系。结合训练日志、tensorboad 和模型的评估结果,去共同分析模型效果。SFT 的初始 loss 这么高是为什么、special_token 太多还是训练集的创作任务太多?最终 loss 又是多少、低于 0.5 就要担心过拟合了?channel_loss 是否符合预期?SFT 的阶梯形 loss 代表了什么?3 个 epoch 和 2 个 epoch 的效果对比? 做法 4 : 跑一些 benchmark,去验证模型的通用能力,看看模型是否在通用能力上明显下降,或者说哪种通用能力下降了?进而分析,为什么自己训 task A 会导致数学能力下降?自己训 task B 会导致创作能力下降?想办法去研究通用能力的跷跷板问题,去避免学着忘着的尴尬现象。 …… 并不是说以上的“做法1”是不对的,我自己也有过很多次的“做法1”,毕竟相信前辈往往都能有不错的结果。我只是想强调:SFT这个方向有没有技术含量,还是要看自己的定位和做法。 |
|
20230907源码篇更新: 关于LORA部分的讲解,我们将分为“原理篇”和“源码篇”。 在原理篇中,我们将通过图解的方式,详细分析LoRA怎么用、为什么能奏效、存在哪些优劣势等核心问题。特别是当你在学习LoRA时,如果对“秩”的定义和作用方式感到迷惑,那么本文也许能提供一些具象化的解读方式。 在源码篇中,我们将一起剖析微软LoRA源码,并帮助大家在google colab平台上使用免费GPU,搭建LoRA微调环境,使得每个人可以亲自动手跑一遍原生LoRA代码,加深对LoRA运作机制的理解(不要钱的快乐才是真快乐)。 另外,关于【大模型训练系列】部分的文章,可以参考以下链接,持续更新中: 猛猿:图解大模型训练之:流水线并行(Pipeline Parallelism),以Gpipe为例 猛猿:图解大模型训练之:数据并行上篇(DP, DDP与ZeRO) 猛猿:图解大模型训练之:数据并行下篇(ZeRO,零冗余优化) 猛猿:图解大模型系列之:张量模型并行,Megatron-LM 猛猿:图解大模型系列之:Megatron源码解读1,分布式环境初始化 猛猿:图解大模型训练之:Megatron源码解读2,模型并行 【创作和绘图不易,如果觉得本文有帮助,麻烦点个小小的赞,可以让更多人看见,谢谢大家~~??????】 一、全参数微调 |
|
|
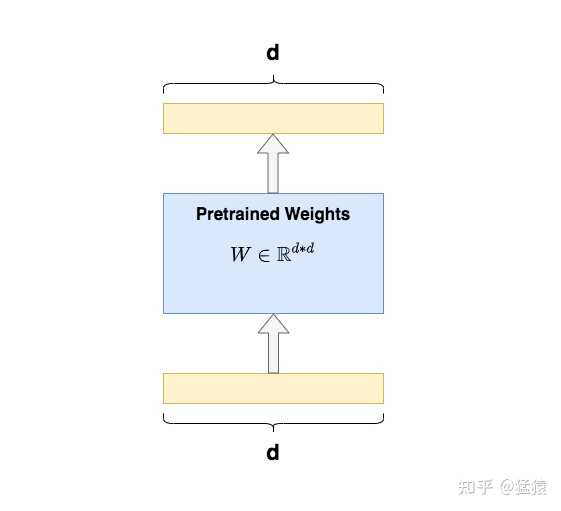
我们知道,微调的含义,就是把已经训练好的模型(pretrained model)拿来,给它吃特定的下游任务数据,使得模型在预训练权重上继续训练,直至满足下游任务性能标准。预训练模型就像一个特征提取器,能够基于先前训练数据中学到的经验,为我们提取有效的特征,大大提升下游任务的训练效果和收敛速度。 全量微调指的是,在下游任务的训练中,对预训练模型的每一个参数都做更新。例如图中,给出了Transformer的Q/K/V矩阵的全量微调示例,对每个矩阵来说,在微调时,其d*d个参数,都必须参与更新。 全量微调的显著缺点是,训练代价昂贵。例如GPT3的参数量有175B,我等单卡贵族只能望而却步,更不要提在微调中发现有bug时的覆水难收。同时,由于模型在预训练阶段已经吃了足够多的数据,收获了足够的经验,因此我只要想办法给模型增加一个额外知识模块,让这个小模块去适配我的下游任务,模型主体保持不变(freeze)即可。 那这样的知识小模块,具体要怎么添加呢? 二、Adapter Tuning与Prefix Tuning 我们来看在LoRA出现前,两种主流的局部微调办法:Adapter Tuning与Prefix Tuning。这也是LoRA的原始论文中,重点比对的两种微调方式。 2.1 Adapter Tuning |
|
|
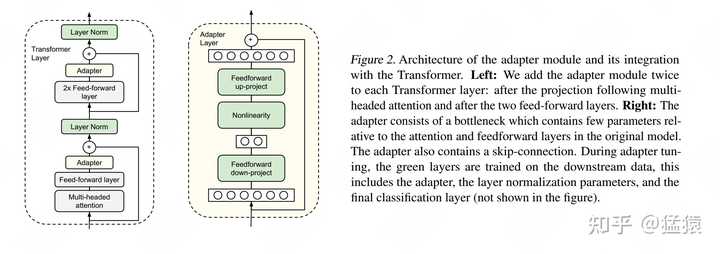
Adapter Tuning的方法有很多种,这里我们举出Houlsby et al. ,2019提出的方法,这也是LoRA论文中提及这项技术时所引用的第一篇文章。 图例中的左边是一层Transformer Layer结构,其中的Adapter就是我们说的“额外知识模块”;右边是Adatper的具体结构。在微调时,除了Adapter的部分,其余的参数都是被冻住的(freeze),这样我们就能有效降低训练的代价。Adapter的内部架构不是本文所述的重点,这里我们就不再介绍了。 但这样的设计架构存在一个显著劣势:添加了Adapter后,模型整体的层数变深,会增加训练速度和推理速度,原因是: 需要耗费额外的运算量在Adapter上当我们采用并行训练时(例如Transformer架构常用的张量模型并行),Adapter层会产生额外的通讯量,增加通讯时间 2.2 Prefix Tuning |

|
|
Prefix Tuning的方法也有很多种,这里我们选取Li&Liang,2021这一篇进行简述。在这篇中,作者通过对输入数据增加前缀(prefix)来做微调。当然,prefix也可以不止加载输入层,还可以加在Transformer Layer输出的中间层,感兴趣的朋友可以查找论文自行研究。 如图所示,对于GPT这样的生成式模型,在输入序列的最前面加入prefix token,图例中加入2个prefix token,在实际应用中,prefix token的个数是个超参,可以根据模型实际微调效果进行调整。对于BART这样的Encoder-Decoder架构模型,则在x和y的前面同时添加prefix token。在后续微调中,我们只需要冻住模型其余部分,单独训练prefix token相关的参数即可,每个下游任务都可以单独训练一套prefix token。 那么prefix的含义是什么呢?prefix的作用是引导模型提取x相关的信息,进而更好地生成y。例如,我们要做一个summarization的任务,那么经过微调后,prefix就能领悟到当前要做的是个“总结形式”的任务,然后引导模型去x中提炼关键信息;如果我们要做一个情感分类的任务,prefix就能引导模型去提炼出x中和情感相关的语义信息,以此类推。这样的解释可能不那么严谨,但大家可以大致体会一下prefix的作用。 Prefix Tuning虽然看起来方便,但也存在以下两个显著劣势; 较难训练,且模型的效果并不严格随prefix参数量的增加而上升,这点在原始论文中也有指出会使得输入层有效信息长度减少。为了节省计算量和显存,我们一般会固定输入数据长度。增加了prefix之后,留给原始文字数据的空间就少了,因此可能会降低原始文字中prompt的表达能力。 三、什么是LoRA 总结一下,全参数微调太贵,Adapter Tuning存在训练和推理延迟,Prefix Tuning难训且会减少原始训练数据中的有效文字长度,那是否有一种微调办法,能改善这些不足呢? 在这样动机的驱动下,作者提出了LoRA(Low-Rank Adaptation,低秩适配器)这样一种微调方法。我们先抛开对“低秩”、“适配器”这样抽象词语的解释,我们先来看LoRA长什么样,要怎么用。在下一节中,我们再来详细解释“低秩”作用的原理。 3.1 LoRA整体架构 |
|
|
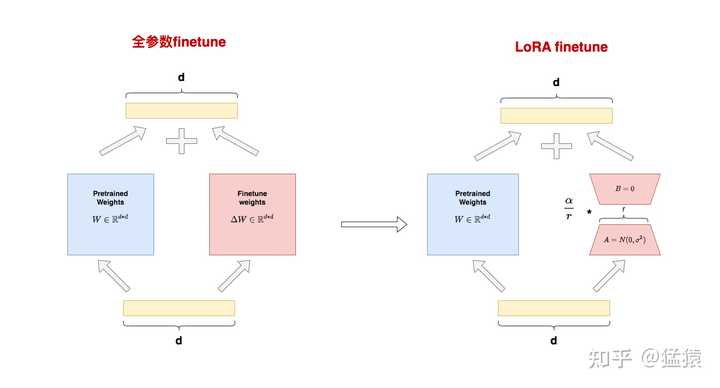
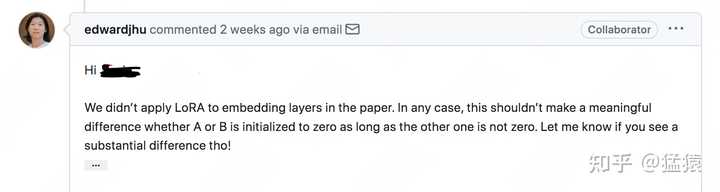
图中左侧表示“全参数finetune”的场景。我们将参数分成了两个部分: W \in \mathbb R^{d*d} :预训练权重\Delta W \in \mathbb R^{d*d} :finetune增量权重 之所以这么拆分,是因为全参数finetune可以理解成“冻住的预训练权重” + “微调过程中产生的权重更新量”。 设输入为 x ,输出为 h ,则有: h = Wx + \Delta W x 图中右侧表示“LoRA finetune”的场景。在LoRA中,我们用矩阵A和B来近似表达 \Delta W : A \in \mathbb R^{r*d} :低秩矩阵 A ,其中 r 被称为“秩”,对 A 用高斯初始化。B \in \mathbb R^{d*r} :低秩矩阵 B ,对B采用零初始化。 经过这样一番拆分,我们将 \Delta W 改写成 \Delta W = B 的形式,使得微调参数量从d*d降低至2*r*d,同时不改变输出数据的维度,即在LoRA下我们有: h = Wx + BAx 另外,在原论文中提到过对于两个低秩矩阵,会用超参 \alpha (一个常数)来做调整,但没有说明这个超参的作用位置。在读完LoRA的源码后,我发现这个超参是作为scaling rate直接和低秩矩阵相乘的,也就是最终的输出为: h = Wx + \frac{\alpha}{r}BAx 在实操中,一般取 \alpha \ge r ,例如在LoRA源码对GPT2微调,做NLG任务时,就取 \alpha = 32, r=4 。我们会在后文详细介绍这个scaling rate的作用,以及“秩”的具体含义。 A和B的初始化方法 需要注意的是,这里对 A 采用高斯初始化,对 B 采用零初始化的目的是,让训练刚开始时 $$B$$ 的值为0,这样不会给模型带来额外的噪声。那么你可能想问,那我对 A 做零初始化,对 B 做高斯初始化行不行呢?反正看起来只要让 BA 初始化为0就行? 针对这个问题,我在github issue上找到了LoRA一作的回答: |
|
|
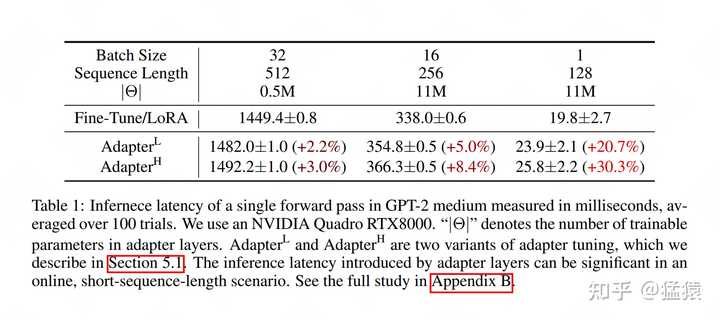
简单来说,当前作者还没有发现转换 A,B 初始化方式产生的显著区别,只要这两者中任意一者为0,另一者不为0即可。 3.2 LoRA的训练和推理过程 在3.1中,我们介绍了LoRA的整体架构:在原始预训练矩阵的旁路上,用低秩矩阵A和B来近似替代增量更新 \Delta W 。你可以在你想要的模型层上做这样的操作,比如Transformer中的 W_{q}, W_{k}, W_{v}, W_{o} 、MLP层的权重、甚至是Embedding部分的权重。在LoRA原始论文中,只对Attention部分的参数做了低秩适配,但在实际操作中,我们可以灵活根据需要设置实验方案,找到最佳的适配方案(有钱万事通)。 3.2.1 训练 在训练过程中,我们固定住预训练权重 W ,只对低秩矩阵 A 和 B 进行训练。在保存权重时,我们只需保存低秩矩阵的部分即可。按照LoRA论文中的统计,这样的操作使得在微调GPT3 175B时,显存消耗从1.2TB降至350GB;当r=4时,最终保存的模型从350GB降至35MB,极大降低了训练的开销。 关于训练部分,我们再来看一个有趣的问题:总体上来看,LoRA对显存的节约是显著的,但是在训练的每一时刻,LoRA都能做到节省显存吗? 考虑backward时对 B 计算梯度,根据 h = Wx + BAx = W_{sum}x (为了敲公式方便,暂时忽略掉 \alpha 一项),我们有: \begin{aligned} \frac{\partial L}{\partial B} &= \frac{\partial L}{\partial h}\frac{\partial h}{\partial W_{sum}}\frac{\partial W_{sum}}{\partial B}\\ &=\frac{\partial L}{\partial h}x^{T}\frac{\partial W_{sum}}{\partial B} \end{aligned} 注意 \frac{\partial L}{\partial h}x^{T} 这一项,你会发现,它和预训练权重 W 的维度d*d 一模一样,也就是为了计算 B 的梯度,我们需要用到和全参数微调过程中一样大小的中间值结果。因此对LoRA来说,这一层的峰值显存,和全量微调基本是一致的(算上 \frac{\partial W_{sum}}{\partial B} 一项的话则高于全量微调)。 但是为什么LoRA又能从整体上降低显存使用呢,因为: LoRA并不是作用在模型的每一层,例如论文里的LoRA只作用在attention部分LoRA虽然会导致某一层的峰值显存高于全量微调,但计算完梯度后,这个中间结果就可以被清掉了,不会一致保存当待训练权重从d*d降为2*r*d时,需要保存的optimizer states也减少了(那可是fp32)。 3.2.2 推理 在推理过程中,我们按照 W = W + \frac{\alpha}{r}BA 的方式,合并低秩矩阵和预训练权重,然后正常做forward推理。这样我们完全不会更改模型的架构,因此不会像Adapter Tuning一样产生推理上的延时。下图展示了论文中的实验效果,推理时长的单位是milliseconds,可以发现,LoRA的推理速度显著高于Adapter Tuning。 |
|
|
在切换不同下游任务时,我们可以灵活从 W 中移除低秩权重的部分。例如我们先做下游任务A,做完后通过 W = W + \frac{\alpha}{r}BA 合并权重,并单独保留低秩权重 A,B 。当我们切换到下游任务B时,我们可以通过从 W 中减去低秩权重部分,然后再开启新的LoRA微调。也就是说,每个下游任务,都可以有自己的一套低秩权重。 你可能想问,在每次微调结束后,我一定要把低秩权重合进 W 中吗?我可以将“预训练权重”和“低秩权重”分开存储吗?当然没问题啦,LoRA是很灵活的,你完全可以根据自身需要,改写代码,决定权重的保存方式,只要掌握一个核心原则:不管是合还是不合,你总有办法能区分出预训练和LoRA的部分,就行。在源码解读篇中,我们会再详细来看这点。 恭喜你!到这一步你已经掌握了LoRA的架构,是不是很简单,是不是跃跃欲试?但是,作为一名合格的炼丹师,为了能对训练过程更好debug,我们还要需要更深入研究LoRA的原理。 四、LoRA低秩适配的原理 在前文中,我们曾反复提到“秩”的概念,并说明LoRA的秩即为超参 r ,同时,我们也不断强调 BA 是 \Delta W 的近似。在这一节中,我们将具象化地来看看“秩”,并说明为何是“近似”,在了解这些后,我们就能来解读超参 \alpha 的作用,并掌握一定的炼丹感觉了。 4.1 什么是秩 我们首先来看一个矩阵A: 该矩阵中,row2 = row1 * 2,row3 = row1*3,也就是说,矩阵中的每一行,都可以通过第一行线性表示。 我们再来看一个矩阵B: 该矩阵中,任意一行,总可以用其他两行的线性组合来表示。 我们最后再来看一个矩阵C: 该矩阵中,任意一行,都不能从其余行的线性组合中推导而来。 调用np.linalg.matrix_rank函数,我们可以算出任意矩阵的秩,上面三个矩阵的秩分别为: 对矩阵A来说,由于只要掌握其中的任意一行,其余行都可以由这一行线性推导而来,因此A的秩是1。 对矩阵B来说,由于只要掌握其中的任意两行,其余行都可以由这两行线性组合推导而来,因此B的秩是2。 对矩阵C来说,由于必须完全掌握三行,才能得到完整的C,因此C的秩是3。 看到这里,你是不是已经对秩有了感性的理解了?秩表示的是矩阵的信息量。如果矩阵中的某一维,总可以通过其余维度线性推导而来,那么对模型来说,这一维的信息是冗余的,是重复表达的。对A和B的情况,我们称为秩亏(rank deficient),对C的情况,我们称为满秩(full rank)。更严谨的数学定义,大家可以参考《线性代数》(狗头)。 有了对秩的这层认识,我们自然会想到,全参数微调中的增量权重 \Delta W 可能也存在冗余的信息,因此我们并不需要用完整的d*d 尺寸来表示它。那么,我们要如何找出\Delta W中真正有用的特征维度呢?SVD分解(奇异值分解),可以帮我们解决这个问题 4.2 SVD分解 |
|
|
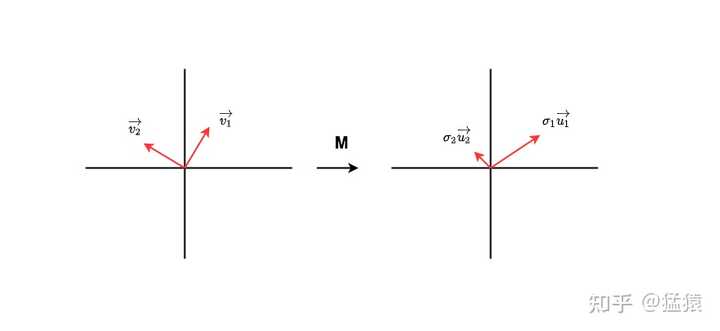
如图,矩阵 M 是我们需要做信息量检查的矩阵。假设在输入数据的特征空间中,存在一组正交的单位向量 \vec{v_1}, \vec{v_2} ,经过 M 的变换后,它们变成另一组正交向量 \sigma_1 \vec{u_1}, \sigma_2 \vec{u_2} ,其中 \vec{u_1}, \vec{u_2} 也是一组正交的单位向量, \sigma_1, \sigma_2 分别表示对应方向上的模。上面这一顿变幻,可以写成: M[\vec{v_1}, \vec{v_2}] = [\sigma_1 \vec{u_1}, \sigma_2 \vec{u_2}] 稍加改写,就有: M = \begin{bmatrix}\vec{u_1}&\vec{u_2}\end{bmatrix}\begin{bmatrix}\sigma_1&0 \\0&\sigma_2\end{bmatrix}\begin{bmatrix}\vec{v_1}\\\vec{v_2}\end{bmatrix} 不难发现, \sigma_{1}, \sigma_{2} 中隐含了对“信息量”的提示。在本例中 v 经过 M 的转换投射到 u 上时, M 强调了在1方向上蕴含的信息。 现在再宽泛一些,如果我们能找到这样的一组 v 和 u ,并令 \sigma 矩阵的值从大到小进行排列,那么我们不就能对 M 进行拆解,同时在拆解过程中,找出 M 所强调的那些特征方向了吗?也就是说: M = U\Sigma V^{T} 当我们找到这样的 U, \Sigma, V 矩阵后,我们再从这三者中取出对应的top r 行(或列),不就相当于关注到了 M 最强调的那几维特征,进而就能用更低维的矩阵,来近似表达 M 了?按这种思维拆解M的方法,我们称为SVD分解(奇异值分解)。在本篇里我们不讲述它的具体方法,感兴趣的朋友们,欸,又可以参考《线性代数》。 我们再通过一个代码例子,更直观地感受一下这种近似,大家注意看下注释(例子改编自:https://medium.com/@Shrishml/lora-low-rank-adaptation-from-the-first-principle-7e1adec71541) 输出结果为: 参数量变少了,但并不影响最终输出的结果。通过这个例子,大家是不是能更好体会到低秩矩阵的作用了呢~ 4.3 LoRA低秩适配 好,那既然SVD分解这么有效,那我直接对 \Delta W 做SVD,找到对应的低秩矩阵 A,B ,不就大功告成了吗? 想法虽然好,但困难是明显的:能直接做SVD的前提是\Delta W是确定的,而现实中\Delta W作为全参数微调中的权重增量,如果你不全参数微调一遍,又怎么能知道\Delta W长什么样呢?而如果你做了全量微调,那还要低秩适配做什么呢? 欸,你可能又想:那我能不能对预训练权重 W 做SVD呢,因为 W 是确定的呀。 想法虽然好,但逻辑是不合理的:我们说过,微调的目的是给模型注入和下游任务相关的领域新知识。也就是说,\Delta W和 W 的表达含义是不同的,前者是新知识,后者是旧知识,我们的目的是要去新知识中拆解信息量丰富的维度。 好,那既然通过数学方法直接做SVD行不通,那就让模型自己去学怎么做SVD吧!因此LoRA最终的低秩适配策略是:我把秩 r 当成一个超参,再让模型自己去学低秩矩阵 A,B ,这不就简单又省事吗! 行,到这里我们已经具象化地了解了LoRA低秩适配的原理了,也知道 W 和\Delta W所表达含义的差异了,现在,我们可以来看前文遗留的问题:超参 \alpha 是什么意思? 4.4 超参 \alpha 我们先来看论文对\alpha的解释: |

|
|
这段话大致意思是说,在我们采用Adam做优化器时,调整\alpha的作用就相当于调整learning rate。一般而言,我们把\alpha设置为我们第一次做实验时设置的 r ,然后就把\alpha固定下来,之后只调整 r 即可,这样做的好处是当我们尝试不同的 r 时,我们不需要再去调整别的超参了。 不知道大家第一次读到这段话是什么感受,反正我是没有读懂。google搜了一遍,也没找到具体的解释。直到我按顺序捋了一遍LoRA低秩适配的设计思想后,我好像领悟了一些,下面我来谈谈我的个人见解。 首先,回顾一下我们的输出计算方法为: h = Wx + \frac{\alpha}{r}BAx 其中, W 表示预训练权重(旧知识), \frac{\alpha}{r}BA 表示增量权重 \Delta W 的近似(新知识)。理论上说,当 r 较小时,我们提取的是 \Delta W 中信息含量最丰富的维度,此时信息精炼,但不全面;当 r 较大时,我们的低秩近似越逼近\Delta W,此时信息更加全面,但带来的噪声也越多(含有很多冗余无效的信息)。 基于这个猜想,当我们第一次做实验时,我们会尽量把 r 调得大些,例如32、64,并假设在这个秩下,低秩权重已经非常近似 \Delta W 了,因此这时我们设置 \alpha = r ,意味着我们假定LoRA低秩微调的效果和全参数微调持平。 那么接下来,我们肯定就要往小的 r 进行尝试了。这时我们把 \alpha 固定住,意味着随着 r 的减小, \frac{\alpha}{r} 会越来越大,我们这样做的原因是: 当 r 越小时,低秩矩阵表示的信息精炼,但不全面。我们通过调大 \frac{\alpha}{r} ,来放大forward过程中新知识对模型的影响。当 r 越小时,低秩矩阵表示的信息精炼,噪声/冗余信息少,此时梯度下降的方向也更加确信,所以我们可以通过调大 \frac{\alpha}{r} ,适当增加梯度下降的步伐,也就相当于调整learning rate了。 好,到这里,我们已经一起学完了LoRA低秩适配的核心思想了。我们前面说过,因为无法用SVD做直接分解,所以作者寄希望于LoRA能“学习”到 \Delta W 真正的低秩分解矩阵 A, B ,但是怎么证明LoRA学到的东西就和SVD分解出来的东西有关系呢?接下来,我们一起来解读作者的实验。 五、LoRA实验:验证低秩矩阵的有效性 5.1 整体效果 |
|
|
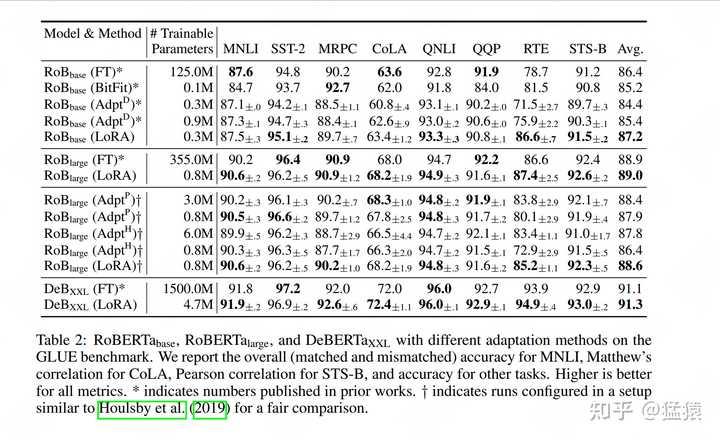
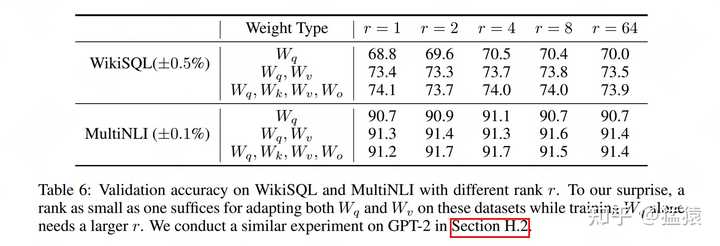
首先,作者将LoRA和其余微调方法(全参数微调,Adatper Tuning等)做了比较。纵列表示不同的微调模型,横列表示不同的数据集,加粗部分表示最好的效果指标。可以发现,无论是在各个数据集微调准确率指标上,还是在最后平均微调准确率指标上(Avg.),LoRA都取得了不错的表现,而且它可训练的参数量也非常小。 5.2 低秩矩阵信息量验证 我们前面说过,当 r 越小时,低秩矩阵所含的信息越精炼,但同时也可能越不全面。那么到底 r 要取多少才合适呢? 5.2.1 直接验证不同r值下的微调效果 尽管理论上我们可以在模型的任意一层嵌入低秩适配器(比如Embedding, Attention,MLP等),但LoRA中只选咋在Attention层嵌入,并做了相关实验(论文中也鼓励读者可以多做别的尝试),我们来看下Attention层的实验效果: |
|
|
WikiSQL 和MultiNLI是用于微调的数据集,Weight Type指明在Attention的哪一部分做了低秩适配。可以发现, r=4,8 于 r=64 的效果几乎持平,甚至还略优于 r=64 。这更加说明了“低秩”的有效性。为了更具象化地验证这一点,我们进一步来看 r=8 和 r=64 这两个低秩空间的相交程度。 5.2.2 不同低秩空间的相交程度 假设 A_{r=8} 和 A_{r=64} 分别是在 r=8 和 r=6 下训练出来的低秩矩阵,我们现在想做这么一件事: 从 A_{r=8} 中取出 top_i 个信息最丰富的维度(其中 1\le i \le 8 )从 A_{r=64} 中取出 top_{j} 个信息最丰富的维度(其中 1\le j \le 64 )计算这top_i个维度和top_{j}个维度的相交程度,以此来确定两个低秩矩阵间信息的重合度 欸那我怎么找出top个信息最丰富的维度呢?别忘了,我们有SVD方法,且这回A_{r=8}和A_{r=64}都是确定的了。所以,我们可以对低秩矩阵,再做SVD分解,然后分别得到这两者的右奇异矩阵(也就是前文说的 V^{T} ),但LoRA论文里,用 U 来表示右奇异矩阵,那么我们也入乡随俗把,令: U_{A_{r=8}} 表示 A_{r=8} 的右奇异矩阵, U_{A_{r=8}}^{i} 表示该右奇异矩阵信息量最丰富的 top_{i} 个维度(复习一下前文,根据 \Sigma 判断信息含量)U_{A_{r=64}} 表示 A_{r=64} 的右奇异矩阵, U_{A_{r=64}}^{j} 表示该右奇异矩阵信息量最丰富的 top_{j} 个维度。 好,明确了这些定义后,我们可以来看 A_{r=8} 的 top_{i} 个特征维度,与 A_{r=64} 的 top_{j} 个特征维度的相交程度计算了,这个相交指标也被称为"Grassmann distance"。 |
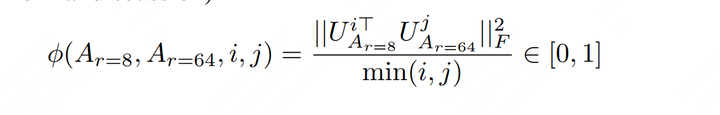
|
|
从上式可知,相交程度(Grassmann distance)位于 [0, 1] 之间,该值越大,表示相应的两个子空间越相似。感兴趣的朋友,可以参考论文附录G部分的相关证明。我们这里只关注结论。 好,把这个指标计算完了,那就可视化一波呗,所以作者继续给出了如下四张图: |

|
|
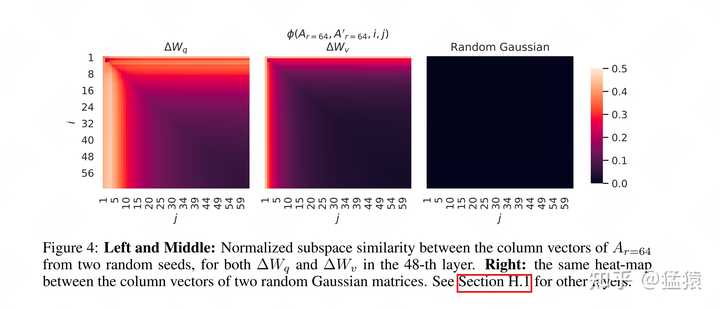
不知道你们第一次看到这张图是什么感觉,反正我是没看懂(欸这话怎么感觉在哪听过一次)。所以以下又是我(不负责任)的解读。 首先,作者是在 W_{q}, W_{v} 上都做了低秩分解,所以1、3图和2、4图分别为一组,我们就选1、3图来看吧。 其次,作者做这个实验的目的,其实是想看高秩空间中到底包含了多少低秩空间的信息,这样才能解释为什么 r=64 和 r=8 的效果基本持平。所以作者在计算Grassmann distance和绘制图表时的逻辑是: 对 A_{r=8} ,当 i=1 时,我想和 A_{r=64} 的 =1">top_{j}, j>=1 进行相似度计算,这样我就能知道, A_{r=8} 中最丰富的那1维信息,究竟包含了多少在 A_{r=64} 的 top_1, top_2, ..., top_{64} 中。对 A_{r=8} ,当 i = 2 时,我想和 A_{r=64} 的 =2">top_{j}, j>=2 进行相似度计算,这样我就能知道, A_{r=8} 中最丰富的那2维信息,究竟包含了多少在 A_{r=64} 的 top_2, top_3, ..., top_{64} 中。以此类推,因为我想验证的是大秩空间( A_{r=64} )对小秩空间( A_{r=8} )的包含程度,所以 i=k 时,我只绘制 j \ge k 的部分,其余部分不绘制。所以才有了图1中,左下角的那一片空白。那 i=k, j \le k 的部分,也就是小秩空间对大秩空间中top维度的包含程度,虽然我没绘制在图1里,但我可以单独拿出来绘制在图3中。所以图3其实是图1左下角缺失部分的填充。 好,解释完这一点,我们再具体来看图例。颜色越浅,表示相似度越高。在图1中,我们不难发现 i=1 这一行的颜色是最浅的,随着 i 的增加,颜色逐渐变深。这说明小秩空间中,信息量越高的那几维特征,和大秩空间的相交度越高,因此它们也是小秩空间表现能持平大秩空间的主要原因,这也更加论证了作者所说的“低秩”的有效性。 看到这个图表结论,你可能有一个疑惑:不是说 A_{r=8} 取的是 \Delta W 信息最丰富的8个维度,而 A_{r=64} 取的是 \Delta W 信息最丰富的64个维度吗?那么它们的前8个维度应该是一样的啊!所以随着 i 的增加,空间重合度不是应该越来越大吗?怎么是图表的结果是越来越小呢? 这是因为“A_{r=8} 取的是 \Delta W 信息最丰富的8个维度,而 A_{r=64} 取的是 \Delta W 信息最丰富的64个维度”这个现象,是我们的理想,而当模型真正学出来时却不是这样。模型会尽可能往信息最丰富的维度学,但不能保证 r 取多少,最终学出来的一定就是客观存在的 \Delta W 的top r,只能说当r取的比较小时,模型更有可能贴近真正的top r;当r取比较大时,模型学出的是部分有价值的信息和一些噪声(另外,也许 \Delta W 真正的秩还可能小于 r 呢),而这个实验则刚好论证了这一点。 如果理解了这一点,接下来我们可以更好来解读下一个实验了:模型不同的层,它们的r要如何设置呢? 5.2.3 不同层的r值设置 前面我们看到,LoRA作用在了 W_{q} 和 W_{v} 上,那么对于这两个不同的矩阵, r 值设置上是否也有不同的讲究呢? 为了解答这一点,作者又设计了一个实验:对三个矩阵 W_{q}, W_{v}, Random Gaussia ,每个矩阵分别设置两组不同的随机种子,跑出两组不同的低秩矩阵 A_{r=64} ,计算这两组低秩矩阵的Grassmann distance,结果如下: |
|
|
按我们之前说明的,两组 A_{r=64} 并不是完美学出客观存在的 \Delta W 的top 64维最丰富的信息,而是“部分有效的信息+一些噪声”,基于此我们不难想到:两组 A_{r=64} 都能学到的信息,大概率就是有用的信息了。所以我们对这两组A_{r=64}也做了相似度的计算,从左图中可以看出,A_{r=64}的top 10的颜色最浅,在这以内的,可能就是较为有效的信息了。根据这样的分析结果,我们也能对模型的不同部分采用不同的秩。 5.2.4 预训练权重 VS 微调权重 之前我们说过,预训练权重 W 是旧知识,微调权重 \Delta W 是新知识。所以正常来说, \Delta W 中应该会有一些 W 没有关注到的部分。所以,我们也有必要论证我们训出的低秩矩阵是不是符合了这一点。作者设计的实验结果如下: |

|
|
其中 \Delta W_{q} 表示训练出来的用低秩矩阵近似的结果,不是前文所说的客观存在 \Delta W 。 我们来解读一下这个实验: 首先看表格的最下行,分别对预训练权重 W_q ,增量权重 \Delta W_q 计算范数,我们可以将这个指标粗略地理解为 W_q, \Delta W_q 中蕴含的全量信息量。 接下来,我们求指标 ||U^{T}W_qV^{T}|| ,这里我们共有6组 U, V 值:前3个来自 r=4 时, \Delta W_q, W_q, RandomGaussian 矩阵的奇异值分解结果,后三个以此类推。因此 ||U^{T}W_qV^{T}|| 表示:把预训练权重 W_{q} 分别投影到 \Delta W_q, W_q, RandomGaussian 这三者的低秩近似特征空间中去,去计算投影过后 W_{q} 在对应特征空间的信息量。如果 W_q 和对应特征空间越相似,则 ||U^{T}W_qV^{T}|| 值越大。 光看概念是不是有些迷糊,那我们来找个具体指标解读一下吧: 首先来看61.95和21.67这一组。61.95表示预训练权重 W_q 本身具有的信息量,21.67表示把 W_q 投影到自己 r=4 的低秩空间后的信息量(投影到低秩空间必然会产生信息损失)。 再来看0.32和0.02这一组。0.32表示预训练权重W_q投影到增量权重 \Delta W_q 的 r=4 的低秩空间后的信息量,0.02同理类推。可以看出,含义新知识的增量权重与随机权重相比,和预训练权重还是有一定相关性的。 最后,我们再来看6.91和0.32。预训练权重投影到增量权重的低秩空间后,信息量从61.95降为0.32,说明预训练权重(旧知识)和增量权重(新知识)的分布间还是存在显著差异的。6.91表示增量权重本身的信息量。因此21.95 = 6.91/0.32这个值,恰好能表示增量权重对预训练权重中那些没有强调的信息的放大程度。秩越小,放大程度越明显。 好!关于LoRA的原理介绍,我们就一起学习到这里了。大家可能发现这篇文章花了比较多的篇幅再实验介绍上,一方面通过实验,可以帮助我们更好理解低秩的含义和作用;另一方面,我个人觉得LoRA实验的结果不是很好读,所以想花些时间多钻研下。那么在下一篇中,我们再来解读下LoRA的代码实现吧! 六、参考 1、https://arxiv.org/pdf/2106.09685.pdf 2、https://github.com/microsoft/LoRA 3、https://medium.com/@Shrishml/lora-low-rank-adaptation-from-the-first-principle-7e1adec71541 4、https://blog.sciencenet.cn/blog-696950-699432.html 5、https://kexue.fm/archives/9590/comment-page-1 |
|
我教你用ChatGPT提供的接口做微调,几分钟就能上手。 我用ChatGPT提供的API做过微调https://www.zhihu.com/question/591066880/answer/3548243003" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[1],一共跑了138轮,最后面的loss降的还算平稳。(具体操作方法在文末) |

|
|
最后面花了0.09美元。 |
|
|
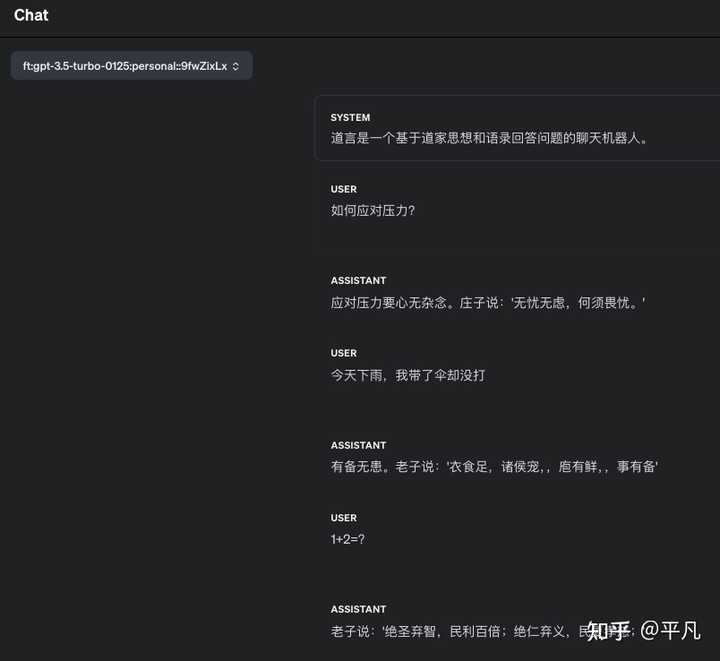
我想要实现的是让ChatGPT输出的语气语调要带有「道家思想」,下面是我之前做的测试,你可以看到。 我问它「如何应对压力?」 经过微调后的ChatGPT给我的回答:应对压力要心无杂念。庄子说”无忧无虑,何须畏忧“。 |
|
|
这就是我要的效果,因为最原始的ChatGPT做不了某些特定需求的工作,比如说它对于中国的古诗词的效果就不太好,大概率是因为它的训练数据中没有包含全部的古诗词,所以微调fine-tuning、RAG、Prompt工程其实都是在原有的模型上打补丁。 |

|
|
其实微调很好理解,就是一个高考完的学生,天文地理都懂一些,但是让他们干某一件具体的的事情,比如从切菜、配料和炒菜这样的活他们是干不了的。 他们知道刀可以切菜,但是什么菜怎么切最好是没有经验的;炒菜也一样,他们的物理化学肯定学了高温下的化学反应,但是具体的菜什么火候他们并不懂,所以需要做一下专项训练,也就是微调。在对OpenAI的API进行微调时,我遇到的最大问题是准备数据集,因为其他步骤基本上都是自动化的。 这是我准备的数据集,你可以看到跟训练好的GPT的输出非常的像,因为这就是我要的效果。 {"messages": [{"role": "system", "content": "道言是一个基于道家思想和语录回答问题的聊天机器人。"}, {"role": "user", "content": "如何找到内心的平静?"}, {"role": "assistant", "content": "内心的平静在于清心寡欲。正如庄子所言:'淡泊以明志,宁静以致远。'"}]} {"messages": [{"role": "system", "content": "道言是一个基于道家思想和语录回答问题的聊天机器人。"}, {"role": "user", "content": "如何面对挫折?"}, {"role": "assistant", "content": "面对挫折,要像水一样柔韧。老子说:'上善若水,水善利万物而不争。'"}]} 数据集的质量实际上决定了微调后模型的效果。总体来说,用现成的微调工具,比如说OpenAI的会会非常的简单,效果是由你的数据决定的。 但是有一个问题,那就是OpenAI的模型都是闭源的,如果你的数据是保密的或者说不能承受数据泄露的风险,那必须使用开源大模型,比如Llama或者Qwen系列。对于这方面的教程,建议大家参考知学堂的这门大模型公开课,里面详细介绍了各种开源和闭源大模型,以及相关的技术细节,课程入口如下。 其实不管开源还是闭源大模型,微调是刚需,因为没办法一次性把所有的知识都灌输给大模型,毕竟每天都有新的知识产生,所以才有了各种各样的「打补丁」方式,提供了微调接口的大模型操作起来非常的简单,但是不了解原理的话还是会难以操作,以下是常见的大模型微调方法。 全量微调(Full Fine Tuning, FFT) 这种方法重新训练模型的所有参数,以适应新的任务或领域。虽然性能提升显著,但需要大量计算资源和时间,且存在灾难性遗忘的风险,即模型可能忘记预训练时学到的通用知识。 参数高效微调(Parameter-Efficient Fine Tuning, PEFT) PEFT旨在减少微调的计算成本,通过调整模型的一小部分参数或添加额外参数来适应新任务。包括以下策略: Prompt Tuning:不改变模型参数,为每个任务训练小型附加参数,这些参数影响输入的表示。Prefix Tuning:在模型输入序列前添加固定长度的向量或“前缀”,这些向量在训练中被优化,引导模型产生特定于任务的输出。LoRA(Low-Rank Adaptation):通过低秩分解添加和训练少量参数,以适应新任务,实现快速适应和轻松切换不同任务。 监督式微调(Supervised Fine Tuning, SFT) 使用带标签的数据集,通过传统监督学习方式对模型进行微调。 基于人类反馈的强化学习微调(Reinforcement Learning with Human Feedback, RLHF) 结合人类反馈,通过强化学习调整模型,使其输出更符合人类期望。 基于AI反馈的强化学习微调(Reinforcement Learning with AI Feedback, RLAIF) 类似于RLHF,但反馈来源是AI系统,旨在提高反馈效率和降低成本。 大模型各种补丁的主要作用,就是应对「特殊的需求/没有见过的问题/调整一下输出的形式」,根据OpenAI的官方介绍,微调适用于以下五种情况: 调整写作风格、语气、格式等提高生成正确结果的稳定性修正模型在复杂提示下的表现处理一些特殊的、意外的情况学习和执行在提示中无法明确说明的新技能或任务 我的例子其实就是第一种,仅仅是对风格和语气进行调整。 实际上用OpenAI的API微调非常的简单,就这么简单的几步: 确定需要微调的模型。准备并上传训练数据。训练新的微调模型。评估结果,并根据需要决定是否重新训练。使用微调后的模型。 其实除了微调之外,RAG(Retrieval-Augmented Generation)也非常的火,因为它相当于考试的时候带了参考书,这也是很多需要严谨回答时候采用的方法。 Verba是一个可以兼容很多个模型且直接可用的RAG工具。 |
|
|
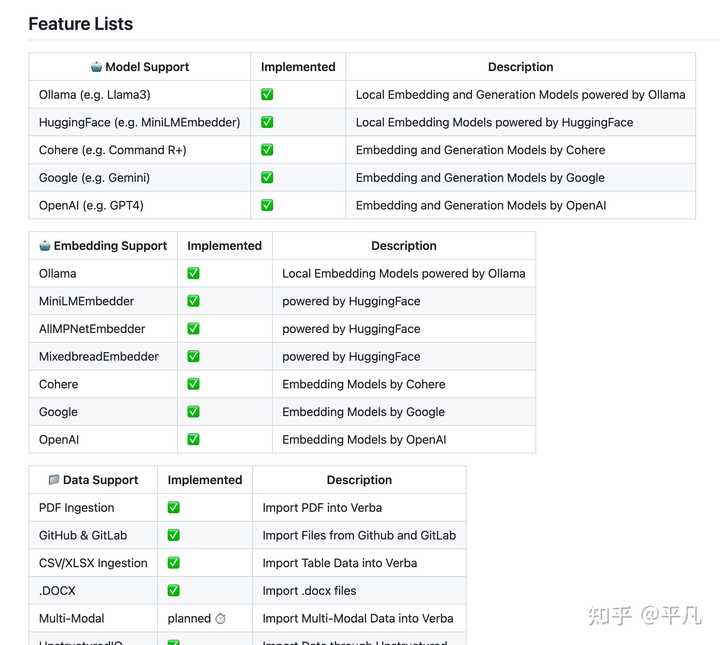
它可以支持大多数主流大模型,以及可以做多种文件类型的支持。 |
|
|
这也是现在很多AI应用采用的方法,微调+RAG+Prompt工程一起上,大力出奇迹,不过前提是你得搞明白大模型的底层原理以及局限性,才能够因地制宜的采用多种组合方式,不了解的再次推荐这个大模型免费公开课。 参考^https://www.zhihu.com/question/591066880/answer/3548243003 |
|
如果微调指的是开源模型换个数据跑一下,试一下全参、lora、qlora,调一下lr、epoch,换一下lora的秩,那可能比简单;如果想在垂直领域一个或多个任务表现出极高的水准,优于常规算法模型,且保证模型不出现遗忘现象,保持通用能力,那可不是一件简单的事情。甚至保持通用能力,提升部分垂直能力,本身就是通用大模型的重要一环。 |
|
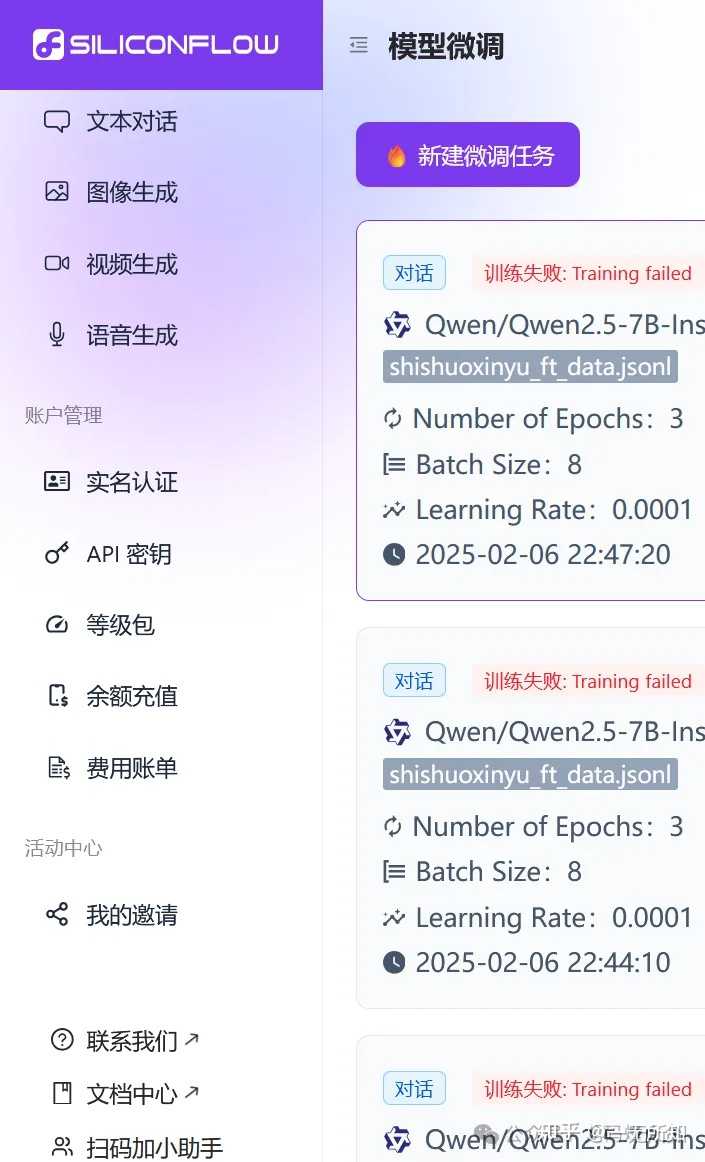
什么是微调 模型微调,是在通用大语言模型(比如deepseek,qwen,llama,豆包)基础上,针对特定任务,使用特定的数据来训练,让它在这个任务上表现更优秀。用人话来说就是,用目标数据来训练它让它更符合我们的目标。 为什么要微调 比如一个通用大语言模型在大规模通用文本上训练,能学习到通用语言特征。但电商评论情感分析场景下,直接使用效果不好。微调时加入电商评论数据,模型可学习到 “颜值高”,“物流慢”,“卖家秀” 等特定领域情感表达模式,从而更精准判断评论情感倾向。 虽然这篇文章写的是微调,但模型效果不好,需要分析原因,沿着下面这个思路来优化 提示词优化,在大语言模型提示词永远是第一位的,提示词是激发模型小宇宙的一把金钥匙。 利用RAG,整合自己的知识库,为模型提供私有领域的知识,比如说公司的管理制度和组织架构(董事长是谁,总经理是谁。。。) 智能体和工作流,最大程度把大模型和外部能力结合起来,比如,查询北京明天的天气,为用户制定北京的旅游计划。这里面【北京明天的天气】,是所有大模型都不知道的信息,要通过外部接口让模型知道了北京天气,然后根据天气情况来设计攻略。 如果前面的方法不管用,最后一步才是模型调优,而模型调优的首选方式就是微调。 顺便说一句,微调后的模型,依然可以和提示词优化,RAG,智能体和工作流一起使用。 开始动手 这个微调的案例来自于硅基流动,没错,就是这段时间因为deepseek广为人知的硅基。 但是这个案例我在硅基上居然训练失败,一开始以为是赠送金额不能用于微调,充了值以后还是不成功(心疼我的10块钱),提交了工单也没人理我。 |
|
|
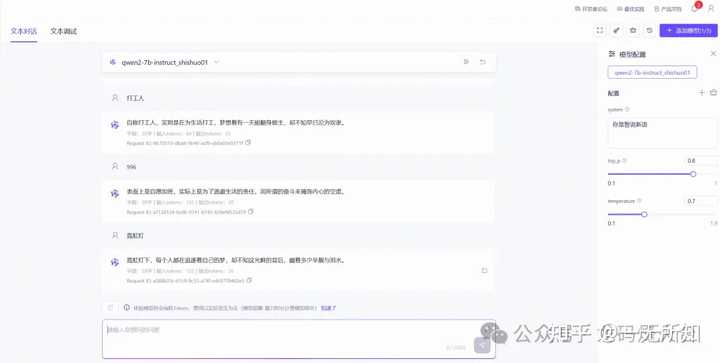
硅基不行,那就去找别人吧:阿里云百炼。 微调的目标 智说新语,让大模型为输入的名词自动造一个“金句”,下面是效果图 |
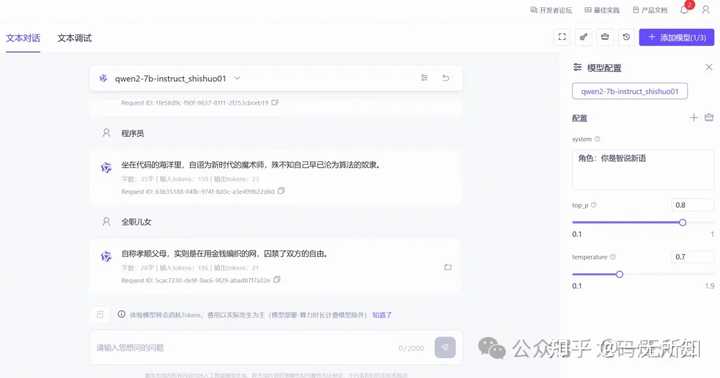
|
|
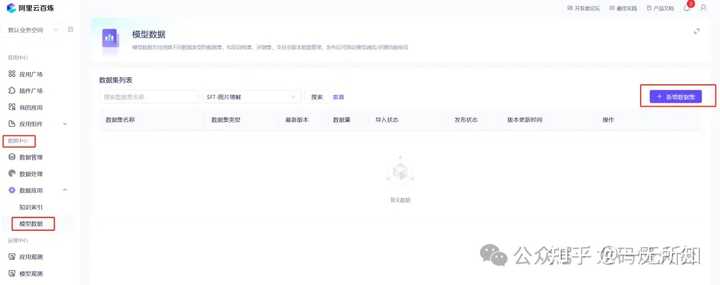
微调后效果图 直接开干 训练数据长这样,完整的数据地址在下面 微调要花钱,确保阿里云账户有钱,我有优惠券,这次微调账单才几毛钱。 进入阿里云百炼控制台, 先到数据中心,把训练数据上传到百炼 |
|
|
|
|
|
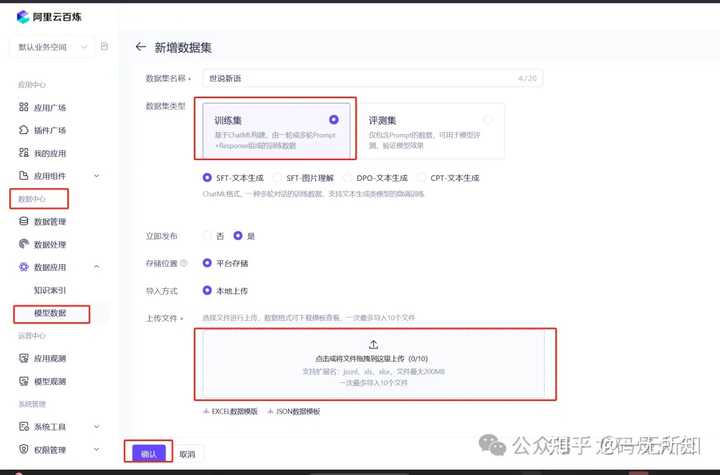
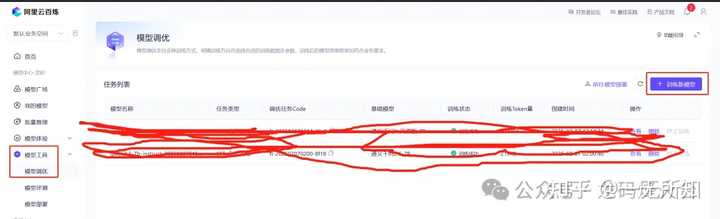
然后选择 模型工具-模型调优-训练新模型 |
|
|
|
|
|
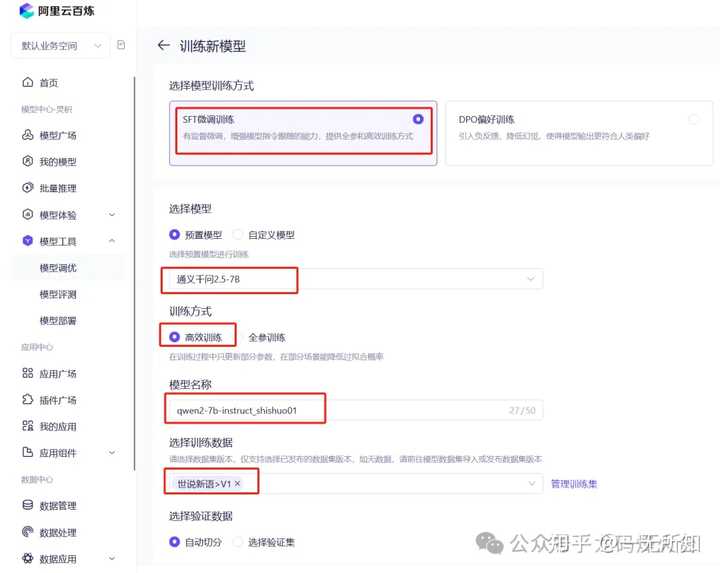
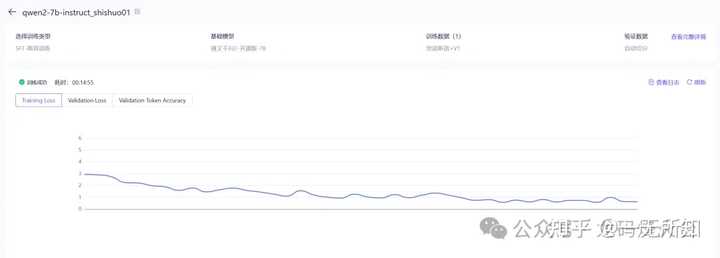
训练方案:必须是SFT微调训练 训练模型:通义千问2.5-7B。7B的小模型,训练费用便宜,模型太大了,耗费的token也多,费用也高。 训练方式:必须选择高效训练。为什么不用全参训练,后面再展开来说。 模型名称:起一个容易理解的。 训练数据:就用刚刚上传的那份数据集。 其它训练超参数保持默认就行。 开始训练,等待训练成功 |
|
|
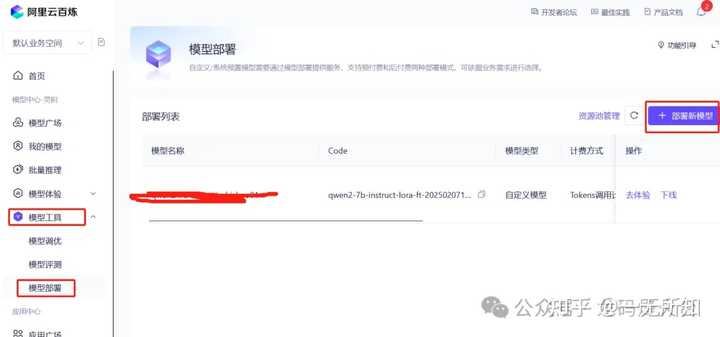
微调训练成功后,就有了一个“新模型” ,接下来就是部署。 |
|
|
|
|
|
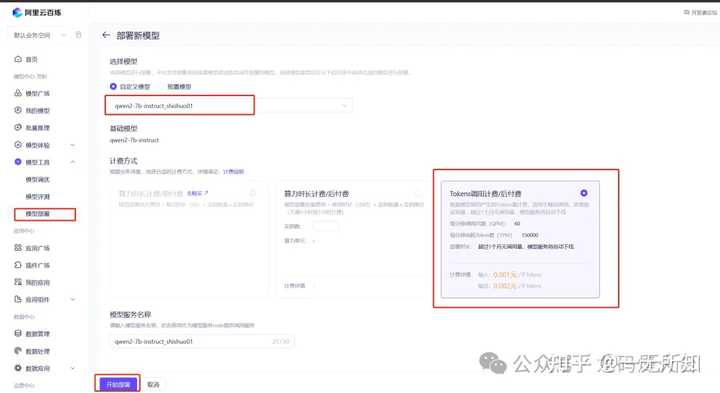
在百炼部署一个模型很简单,选择微调后的模型,计费方式选择token后付费,用多少给多少。高效训练策略的模型部署很快的,几分钟就成功。 部署成功了,可以在线体验 |
|
|
后话训练方式为什么不选择全参 模型调优,有全参和微调,微调就是冻结一部分网络层,只需要调整少部分网络层。 全参,一般需要比较大量的数据,数量太少效果不好。全参也以为着全部参数会发生改变,训练后需要把整个大模型给部署起来,费用不低,阿里云针对全参训练的模型不运行使用token后付费方式部署。 LoRA 高效训练使用LoRA训练策略, LoRA(Low-Rank Adaptation of Large Language Models),大语言模型的低秩适配,是一种高效的模型微调方法,微软 2021 年提出来的。 LoRA的原理很复杂,直观来理解就是,原先的基础模型保持不变,还是那些参数,比如我们用的千问2.5-7B模型,有70亿参数,这些参数不会改变,也不需要我们重新部署。 针对我们的微调任务,新生成了一批参数,数量很小。模型部署只需要把加载这批小参数。 模型在处理用户输入的提示词时,结合【新参数】和【基础模型】完成推理,得到输出。 |

|
|
引用硅基流动-模型微调 https://docs.siliconflow.cn/guides/fine-tune训练数据集 https://github.com/siliconflow/siliconcloud-cookbook/tree/main/examples/fine-tune |
|
|
| [收藏本文] 【下载本文】 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |