[设计艺术] 如何把画框挂在三颗钉子上，使得去掉任意一颗钉子，画框都会掉下去？

天天财汇购物网址万年历小说 | 三峰软件小游戏视频

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

首页淘股吧股票涨跌实时统计涨停板选股股票入门股票书籍股票问答分时图选股跌停板选股 K线图选股成交量选股 [平安银行]

股市论谈均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

商业财经科技知识汽车百科工程技术自然科学家居生活设计艺术财经视频游戏--

天天财汇 -> 设计艺术 -> 如何把画框挂在三颗钉子上，使得去掉任意一颗钉子，画框都会掉下去？ -> 正文阅读

[设计艺术]如何把画框挂在三颗钉子上，使得去掉任意一颗钉子，画框都会掉下去？

[收藏本文] 【下载本文】

看了Matrix67的博客 Matrix67: The Aha Moments 里面提到对于任意数量的钉子，一个都不能少的悬挂方法都是存在的，并且可以…

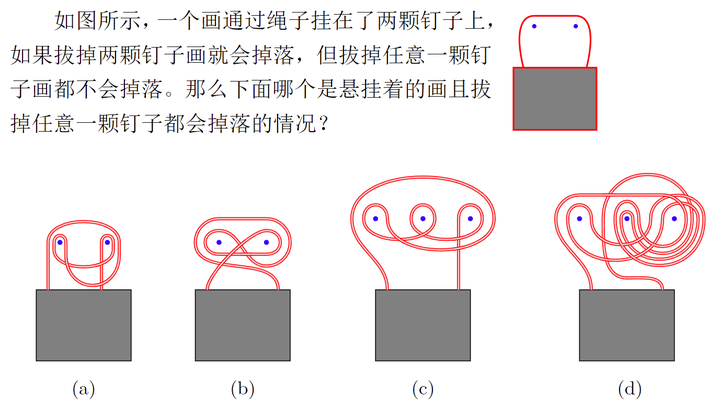
这是一个类似「T8模拟考」的题目，其来源于一类「挂画问题」。

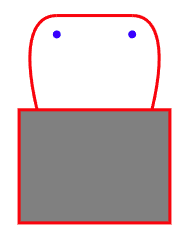
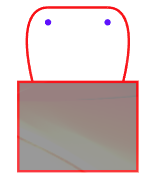
考虑简单的情况，墙上有两颗钉子，通过绳子正常挂上去，如果一个钉子掉落，那么画还会挂在另一颗钉子上。

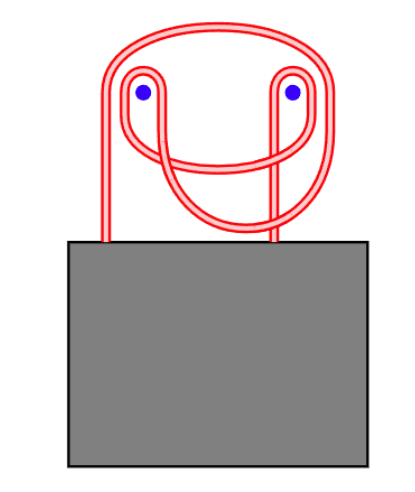
问题是如何把画挂起来，使得拔掉其中任何一颗钉子，画就会掉下来？
记顺时针绕第一颗钉子一周记作 a" role="presentation">aa ,逆时针绕第一颗钉子一周记作 a−1" role="presentation">a?1a^{-1} 。同理，记顺时针绕第二颗钉子一周记作 b" role="presentation">bb ，逆时针绕第二颗钉子一周记作 b−1" role="presentation">b?1b^{-1} ，那么下图的缠绕方法就是 aba−1b−1" role="presentation">aba?1b?1aba^{-1}b^{-1}

如果拔掉第一颗钉子就是将 a" role="presentation">aa 和 a−1" role="presentation">a?1a^{-1} 从 aba−1b−1" role="presentation">aba?1b?1aba^{-1}b^{-1} 中去掉，变成 bb−1=1(无缠绕)" role="presentation">无缠绕bb?1=1(无缠绕)bb^{-1}=1(无缠绕) 。同理拔掉第二颗钉子就会变成 aa−1=1" role="presentation">aa?1=1aa^{-1}=1 。
因此记 n" role="presentation">nn 个钉子的缠绕方式为 Sn" role="presentation">SnS_n ，则易知 n+1" role="presentation">n+1n+1 的情形为 Sn+1={Sn,xn+1}=Snxn+1Sn−1xn+1−1" role="presentation">Sn+1={Sn,xn+1}=Snxn+1Sn?1xn+1?1S_{n+1}=\{S_n,x_{n+1}\}=S_nx_{n+1}S_n^{-1}x_{n+1}^{-1} 。因此，当 n=3" role="presentation">n=3n=3 时，去掉任意一颗钉子使得画掉落的悬挂方式为
{{a,b},c}={aba−1b−1,c}=aba−1b−1c(aba−1b−1)−1c−1=aba−1b−1cbab−1a−1c−1" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">{{a,b},c}={aba?1b?1,c}=aba?1b?1c(aba?1b?1)?1c?1=aba?1b?1cbab?1a?1c?1\begin{align} \{\{a,b\},c\}&=\{aba^{-1}b^{-1},c\}\\ &=aba^{-1}b^{-1}c(aba^{-1}b^{-1})^{-1}c^{-1}\\ &=aba^{-1}b^{-1}cbab^{-1}a^{-1}c^{-1} \end{align}\\ 回到原题，其中 B" role="presentation">BB 选项对应的是 bab−1a−1" role="presentation">bab?1a?1bab^{-1}a^{-1} 。去除第一颗钉子为 aa−1=1" role="presentation">aa?1=1aa^{-1}=1 ，去除第二颗钉子为 bb−1=1" role="presentation">bb?1=1bb^{-1}=1 ，因此成立。
对于 C" role="presentation">CC 选项，对应的情况为 abca−1b−1c−1" role="presentation">abca?1b?1c?1abca^{-1}b^{-1}c^{-1} ，去掉任何一颗都不能让画掉落，因此不选择。

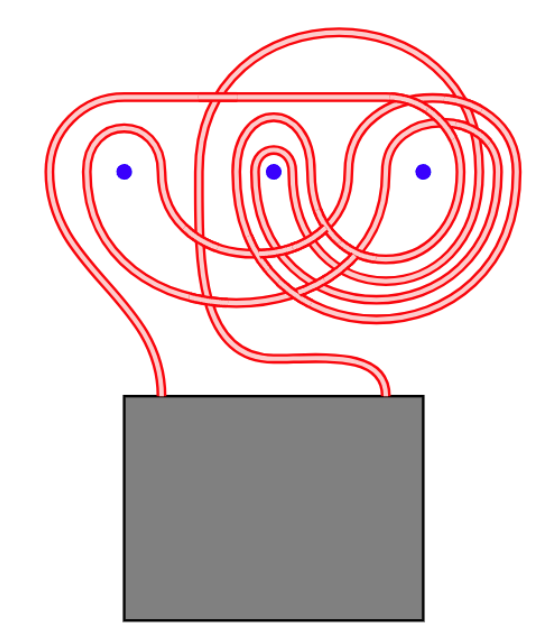
对于 D" role="presentation">DD 选项，对应的情况是 abcb−1c−1a−1cbc−1b−1" role="presentation">abcb?1c?1a?1cbc?1b?1abcb^{-1}c^{-1}a^{-1}cbc^{-1}b^{-1}
对公式进行化简
abcb−1c−1a−1cbc−1b−1=a(bcb−1c−1)a−1(bcb−1c−1)−1={a,bcb−1c−1}={a,{b,c}}" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">abcb?1c?1a?1cbc?1b?1=a(bcb?1c?1)a?1(bcb?1c?1)?1={a,bcb?1c?1}={a,{b,c}}\begin{align} abcb^{-1}c^{-1}a^{-1}cbc^{-1}b^{-1}&=a(bcb^{-1}c^{-1})a^{-1}(bcb^{-1}c^{-1})^{-1}\\ &=\{a,bcb^{-1}c^{-1}\}\\ &=\{a,\{b,c\}\} \end{align}\\ 如果对公式化简困难也可以分别去掉 aa−1,bb−1,cc−1" role="presentation">aa?1,bb?1,cc?1aa^{-1},bb^{-1},cc^{-1}
abcb−1c−1a−1cbc−1b−1a:abcb−1c−1a−1cbc−1b−1b:abcb−1c−1a−1cbc−1bc:abcb−1c−1a−1cbc−1b−1" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">abcb?1c?1a?1cbc?1b?1a:abcb?1c?1a?1cbc?1b?1b:abcb?1c?1a?1cbc?1bc:abcb?1c?1a?1cbc?1b?1\begin{align} &abcb^{-1}c^{-1}a^{-1}cbc^{-1}b^{-1}\\ a:&\phantom{a}b\color{blue}{c}\color{red}{b^{-1}}\color{green}{c^{-1}\phantom{a^{-1}}c}\color{red}{b}\color{blue}{c^{-1}}b^{-1}\\ b:&\color{red}{a}\phantom{b}\color{green}{c\phantom{b^{-1}}c^{-1}}\color{red}{a^{-1}}\color{green}{c\phantom{b}c^{-1}}\phantom{b}\\ c:&\color{red}{a}\color{green}{b\phantom{c}b^{-1}}\phantom{c^{-1}}\color{red}{a^{-1}}\phantom{c}\color{green}{b\phantom{c^{-1}}b^{-1}} \end{align}\\

因此选择 ABD" role="presentation">ABDABD
对于 n" role="presentation">nn 颗钉子的构造，可以发现随着 n" role="presentation">nn 的增大， Sn" role="presentation">SnS_n 需要展开的次数就更多，而 Sn" role="presentation">SnS_n 项数为 2n+2n−1−2" role="presentation">2n+2n?1?22^n+2^{n-1}-2 ，这意味着较多钉子的情况计算速度往往会指数级增加，不过 Ed Pegg Jr. 在这里给出了一个多项式的构造。
记一颗钉子时
E(i:i)=xi" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">E(i:i)=xiE(i:i)=x_i\\ 在添加一颗钉子的情况
E(i:i+1)={xi,xi+1}=xixi+1xi−1xi+1−1" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">E(i:i+1)={xi,xi+1}=xixi+1xi?1xi+1?1E(i:i+1)=\{x_i,x_{i+1}\}=x_ix_{i+1}x_i^{-1}x_{i+1}^{-1}\\ 对于任意的 i" role="presentation">ii 到 j" role="presentation">jj 的区间，有
E(i:j)={E(i:⌊i+j2⌋),E(⌊i+j2⌋+1:j)}" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">E(i:j)={E(i:?i+j2?),E(?i+j2?+1:j)}E(i:j)=\left\{E\left(i:\left\lfloor\frac{i+j}{2}\right\rfloor\right),E\left(\left\lfloor\frac{i+j}{2}\right\rfloor+1:j\right)\right\}\\ 例如
E(1:4)={E(1:2),E(3:4)}=E(1:2)E(3:4)E(1:2)−1E(3:4)−1=(x1x2x1−1x2−1)(x3x4x3−1x4−1)(x1x2x1−1x2−1)−1(x3x4x3−1x4−1)−1=x1x2x1−1x2−1x3x4x3−1x4−1x1x2x2−1x1−1x4x3x4−1x3−1." role="presentation" style="font-size: 100%; display: inline-block; position: relative;">E(1:4)={E(1:2),E(3:4)}=E(1:2)E(3:4)E(1:2)?1E(3:4)?1=(x1x2x1?1x2?1)(x3x4x3?1x4?1)(x1x2x1?1x2?1)?1(x3x4x3?1x4?1)?1=x1x2x1?1x2?1x3x4x3?1x4?1x1x2x2?1x1?1x4x3x4?1x3?1.\begin{align} E(1:4)&=\{E(1:2),E(3:4)\}\\ &=E(1:2)E(3:4)E(1:2)^{-1}E(3:4)^{-1}\\ &=(x_1x_2x_1^{-1}x_2^{-1})(x_3x_4x_3^{-1}x_4^{-1})(x_1x_2x_1^{-1}x_2^{-1})^{-1}(x_3x_4x_3^{-1}x_4^{-1})^{-1}\\ &=x_1x_2x_1^{-1}x_2^{-1}x_3 x_4x_3^{-1}x_4^{-1}x_1x_2x_2^{-1}x_1^{-1}x_4x_3x_4^{-1}x_3^{-1}.\end{align}\\ 在 n≥4" role="presentation">n≥4n\geq4 的情况下，展开的次数减少了并且这还是一个更短的答案，只使用了 16" role="presentation">1616 个符号。
另外，是否还有其他对应的方法？

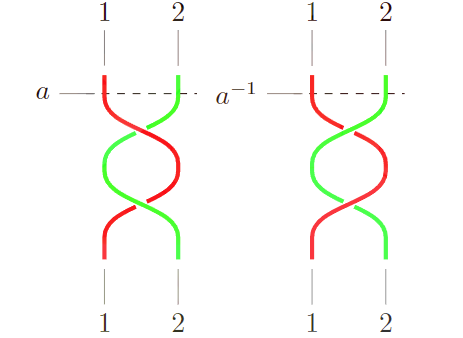
对于上图中的 aba−1b−1" role="presentation">aba?1b?1aba^{-1}b^{-1} ，如果记 a,a−1" role="presentation">a,a?1a,a^{-1} 分别为如下图操作（对1号绳与2号绳进行不同方向的缠绕一圈）

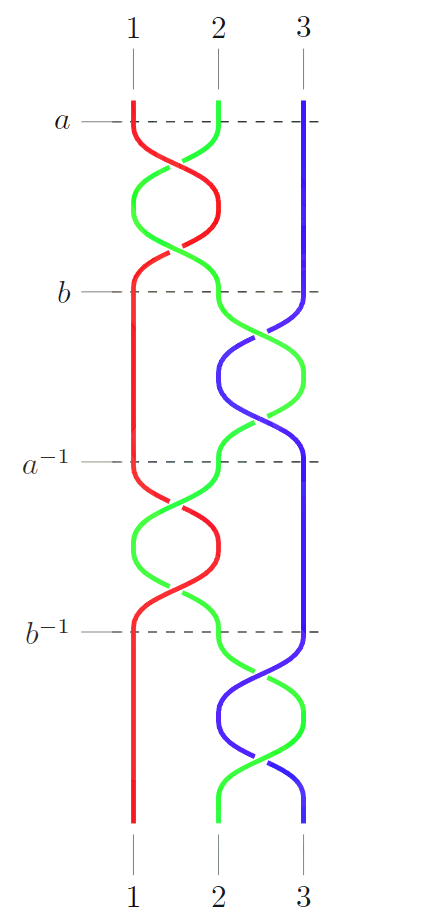
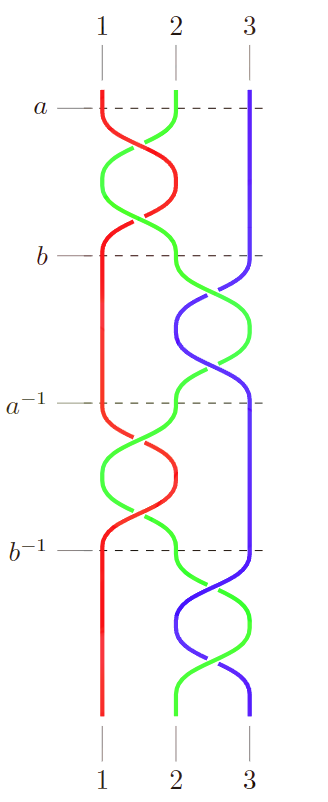
而 b,b−1" role="presentation">b,b?1b,b^{-1} 同理，对2号绳与3号绳进行不同方向的缠绕一圈，那么 aba−1b−1" role="presentation">aba?1b?1aba^{-1}b^{-1} 等价于如下的绳结

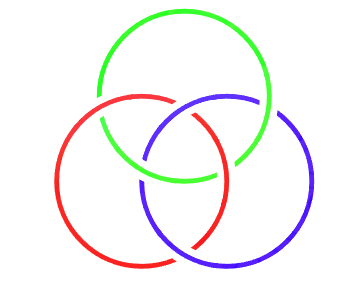
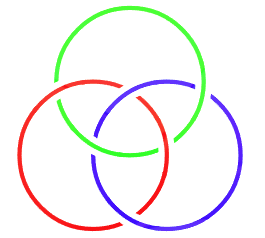
此时将1、2、3号绳的两端首尾拼接，即得到 Borromean rings。

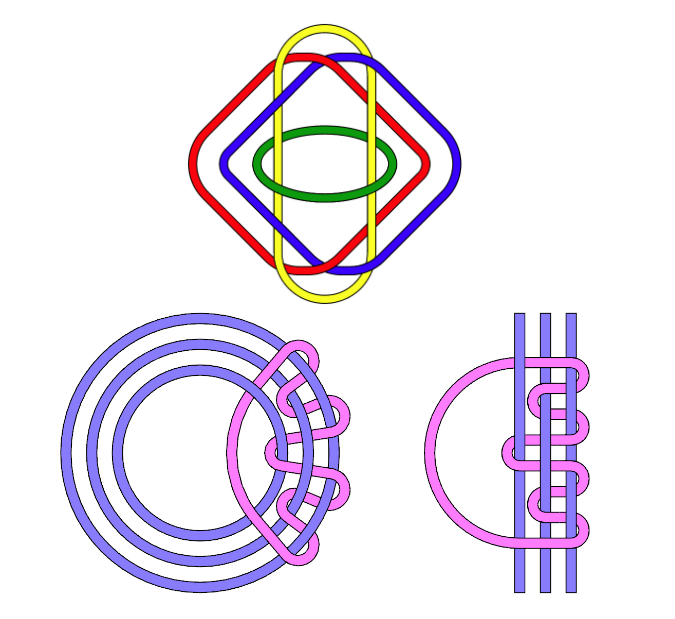
取下其中一环，其余的两环分离，也就是将「钉子」转化为「环」。
同样对于三颗钉子的情况如下

那么考虑更加一般的情况，如果希望在三颗钉子挂画的时候，使得拔掉任意一颗钉子不掉，但拔掉任意两颗钉子画掉，又该如何做呢？
其实答案已经给出了，就是原题的 C" role="presentation">CC 选项。

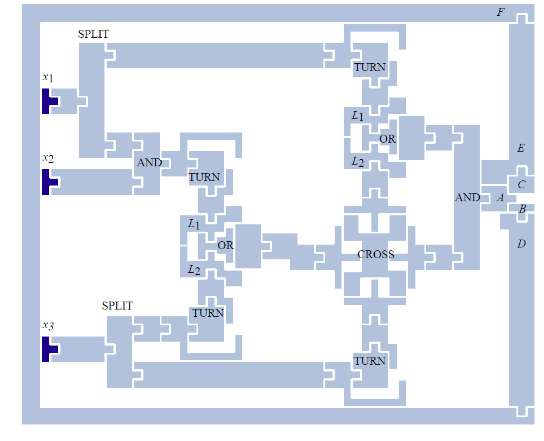
其对应为 abca−1b−1c−1" role="presentation">abca?1b?1c?1abca^{-1}b^{-1}c^{-1} 不难推出只剩一颗钉子的时候画会掉落，而只剩两颗钉子的时候就退化为原来的两颗钉子的挂画问题。
更一般地，考虑对 n" role="presentation">nn 颗钉子赋予布尔变量 xi,1≤i≤n" role="presentation">xi,1≤i≤nx_i,1\leq i\leq n 有
xi:={1,拔掉第i颗钉子;0,保留第i颗钉子;" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">拔掉第颗钉子保留第颗钉子xi:={1,拔掉第i颗钉子;0,保留第i颗钉子;x_i:=\begin{cases} 1,&拔掉第i颗钉子;\\ 0,&保留第i颗钉子;\\ \end{cases}\\ 同时定义极小失效集 ri" role="presentation">rir_i ，也就是拔掉最少的钉子使得画掉落构成的集合，有
f(r1,r2,…,rn)=r1∨r2∨⋯∨rn={1,画掉落;0,画悬挂." role="presentation" style="font-size: 100%; display: inline-block; position: relative;">画掉落画悬挂f(r1,r2,…,rn)=r1∨r2∨?∨rn={1,画掉落;0,画悬挂.f(r_1,r_2,\ldots,r_n)=r_1\vee r_2\vee\cdots\vee r_n=\begin{cases}1,&画掉落;\\0,&画悬挂.\end{cases}\\ 不难验证当 r1≤r1′,r2≤r2′,…,rn≤rn′" role="presentation">r1≤r1′,r2≤r2′,…,rn≤rn′r_1\leq r_1',r_2\leq r_2',\ldots, r_n\leq r_n' 时，有
f(r1,r2,…,rn)≤f(r1′,r2′,…,rn′)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">f(r1,r2,…,rn)≤f(r1′,r2′,…,rn′)f(r_1,r_2,\ldots,r_n)\leq f(r_1',r_2',\ldots,r_n')\\ 也就是说 f" role="presentation">ff 是布尔单调递增函数，换句话说就是不存在「拔掉任意一颗钉子掉落，但拔掉两颗钉子却悬挂」类似的情况。
那么下面试着解决这个问题。
在三颗钉子挂画的时候，使得拔掉任意一颗钉子不掉，但拔掉任意两颗钉子画掉
首先给出极小失效集
\{\{x_1,x_2\},\{x_2,x_3\},\{x_3,x_1\}\}\\ 计算 f 得出
\begin{align} f&=(x_1\wedge x_2)\vee(x_2\wedge x_3)\vee(x_3\wedge x_1)\\ &=(x_1x_2)\vee(x_2x_3)\vee(x_3x_1)\\ &=(x_1x_2x_2x_3x_2^{-1}x_1^{-1}x_3^{-1}x_2^{-1})\vee(x_3x_1)\\ &=x_1x_2x_2x_3x_2^{-1}x_1^{-1}x_3^{-1}x_2^{-1}x_3x_1x_2x_3x_1x_2x_3^{-1}x_2^{-1}x_2^{-1}x_1^{-1}x_1^{-1}x_3^{-1} \end{align}\\ 又或着直接由极小失效集拼接
\begin{align} &\{\{x_1,x_2\},\{x_2,x_3\},\{x_3,x_1\}\}\\ \Rightarrow& (x_1x_2x_1^{-1}x_2^{-1})(x_2x_3x_2^{-1}x_3^{-1})(x_3x_1x_3^{-1}x_1^{-1})\\ =&x_1x_2x_1^{-1}x_3x_2^{-1}x_1x_3^{-1}x_1^{-1} \end{align}\\ 可以看出以上两种方法都不一定能计算出来最小解。
对于挂画问题，得出单调递增布尔函数后，也可以用互锁多边形(interlocked polygons)来解决。

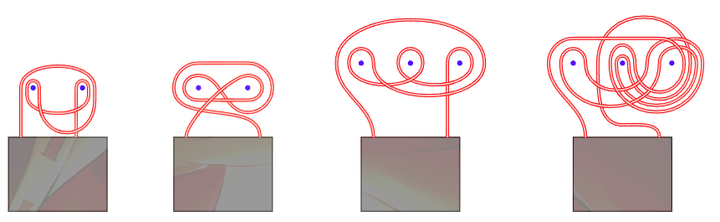
看到最后，可以试着玩一下这些问题了，看看你能想到的最短的解法是什么？https://arxiv.org/pdf/1203.3602" data-tooltip-richtext="1" data-tooltip-preset="white" data-tooltip-classname="ztext-reference-tooltip">[1]
(1-out-of-3) 将一幅画挂在三个钉子上，移除任何一个钉子就会使该画掉落。
(2-out-of-3) 将一幅画挂在三个钉子上，拆下任意两颗钉子后，画就会掉落，但拆下任意一颗钉子后，画仍会挂着。
(1+2-out-of-3) 将一幅画挂在三个钉子上，去掉第一个钉子，画就会掉落，去掉第二个和第三个钉子也会掉落，但只去掉第二个或第三个钉子画仍然挂着。
(1-out-of-4) 将一幅画挂在四个钉子上，移除任何一个钉子就会使该画掉落。
(2-out-of-4) 将一幅画挂在四个钉子上，去掉任何两个钉子就会使画掉落，但去掉任何一个钉子后，画仍会挂着。
(3-out-of-4) 将一幅画挂在四个钉子上，去掉任何三个钉子就会使画掉落，但只要去掉一个或两个钉子，画仍会挂着。
(2+2-out-of-2+2) 将一幅画挂在两个红色钉子和两个蓝色钉子上，去掉两个红色钉子或去掉两个蓝色钉子后，画就会掉落，但去掉每种颜色的一个钉子，画仍会挂着。
(1+2-out-of-2+2) 将一幅画挂在两个红色钉子和两个蓝色钉子上，去掉任何一个红色钉子或去掉两个蓝色钉子后，画就会掉落，但只去掉一个蓝钉子，画仍会挂着。
(1+3-out-of-3+3) 将一幅画挂在三个红钉子和三个蓝钉子上，去掉任何一个红钉子或去掉所有三个蓝钉子，就会使画掉落，但只去掉一个或两个蓝色钉子，画仍会挂着。
(1+2-out-of-3+3) 将一幅画挂在三个红色钉子和三个蓝色钉子上，去掉任何一个红色钉子或去掉任意两个蓝色钉子，就会使画掉落，但只去掉一颗蓝色钉子，画仍会挂着。
(1+1-out-of-2+2+2) 将一幅画挂在两个红色钉子、两个绿色钉子和两个蓝色钉子上，去除两个不同颜色的钉子，就会使画掉落，但去除两个相同颜色的钉子，画仍会挂着。
@Daphnoretin
在评论区问到图是怎么绘制的，是里面大部分图使用 \LaTeX 绘制的，下面放出一些代码

%\usepackage{amsmath}
%\usepackage{tikz}
%\usepackage{graphicx}
%\usetikzlibrary{knots}
%\usetikzlibrary{braids}

\begin{tikzpicture}[every path/.style={red,thick}, every node/.style={transform shape, knot crossing, inner sep=1.5pt}, scale=0.35]
\node (a) at (1.5,-0.1) {};
\node (b) at (-1.5,-0.1) {};
\fill[color=blue] (-1,2) circle (3pt);
\fill[color=blue] (1,2) circle (3pt);
\filldraw[fill=gray] (-2,0) -- (2,0) -- (2,-3) -- (-2,-3) -- cycle;
\draw (b) .. controls (-2,2) and (-1.5,2.5) .. (-1,2.5);
\draw (a) .. controls (2,2) and (1.5,2.5) .. (1,2.5);
\draw (-1,2.5) -- (1,2.5);
\end{tikzpicture}

%\usepackage{amsmath}
%\usepackage{tikz}
%\usepackage{graphicx}
%\usetikzlibrary{knots}
%\usetikzlibrary{braids}

%a
\begin{tikzpicture}[scale=0.4]
    \filldraw[fill=gray] (-2,1) -- (2,1) -- (2,-2) -- (-2,-2) -- cycle;
    \fill[color=blue] (-1,3) circle (3pt);
    \fill[color=blue] (1,3) circle (3pt);
\begin{knot}[
consider self intersections=no splits,
end tolerance=0.5pt,
flip crossing/.list={},
clip width=0.5,
clip radius=1pt,
]
\strand[
red, double=red!20,
line width=0.4pt, double distance=0.7pt,
] (-1.5,1) to (-1.5,3) 
    to[out=90, in=90, looseness=1] (1.5,3)
    to (1.5,2.5)
    to[out=-90, in=-90, looseness=2] (-0.75,2.5)
    to (-0.75,3)
    to[out=90, in=90, looseness=2] (-1.25,3)
    to (-1.25,2.7)
    to[out=-90, in=-90] (1.25,2.7) 
    to (1.25,3)
    to[out=90, in=90, looseness=2] (0.75,3)
    to (0.75,1);
\end{knot}
\end{tikzpicture}

%b
\begin{tikzpicture}[scale=0.4]
    \filldraw[fill=gray] (-2,1) -- (2,1) -- (2,-2) -- (-2,-2) -- cycle;
    \fill[color=blue] (-1,3) circle (3pt);
    \fill[color=blue] (1,3) circle (3pt);
\begin{knot}[
consider self intersections=no splits,
end tolerance=0.5pt,
flip crossing/.list={},
clip width=0.5,
clip radius=1pt,
]
\strand[
red, double=red!20,
line width=0.4pt, double distance=0.7pt,
] (-1.5,1) to[out=90, in=180, looseness=0.5] (1,3.5)
    to [out=0, in=0 ,looseness=2] (1,2.5)
    to (-1,2.5)
    to[out=180, in=180, looseness=2] (-1,3.5)
    to[out=0, in=180, looseness=1] (1,2)
    to[out=0, in=-90, looseness=1] (2,3)
    to[out=90, in=0, looseness=1] (1,4)
    to (-1,4)
    to [out=180, in=90, looseness=1] (-2,3)
    to[out=-90, in=90, looseness=1] (1.5,1);
\end{knot}
\end{tikzpicture}

%c
\begin{tikzpicture}[scale=0.4]
    \filldraw[fill=gray] (-2,1) -- (2,1) -- (2,-2) -- (-2,-2) -- cycle;
    \fill[color=blue] (-2,4) circle (3pt);
    \fill[color=blue] (0,4) circle (3pt);
    \fill[color=blue] (2,4) circle (3pt);
\begin{knot}[
consider self intersections=no splits,
end tolerance=0.5pt,
flip crossing/.list={},
clip width=0.5,
clip radius=1pt,
]
\strand[
red, double=red!20,
line width=0.4pt, double distance=0.7pt,
] (-1.5,1) to[out=90, in=-90] (-3,4)
    to[out=90, in=90, looseness=1] (3,4)
    to[out=-90, in=-90, looseness=1] (-1.5,4)
    to [out=90, in=90, looseness=2] (-2.5,4)
    to [out=-90, in=-90, looseness=1] (0.5,4)
    to [out=90, in=90, looseness=2] (-0.5,4)
    to [out=-90, in=-90, looseness=1] (2.5,4)
    to[out=90, in=90, looseness=2] (1.5,4)
    to (1.5,1);
\end{knot}
\end{tikzpicture}

%d
\begin{tikzpicture}[scale=0.4]
    % \draw[help lines] (-5,-3) grid (5,7);
    \filldraw[fill=gray] (-2,1) -- (2,1) -- (2,-2) -- (-2,-2) -- cycle;
    \fill[color=blue] (-2,4) circle (3pt);
    \fill[color=blue] (0,4) circle (3pt);
    \fill[color=blue] (2,4) circle (3pt);
\begin{knot}[
consider self intersections=no splits,
end tolerance=0.5pt,
flip crossing/.list={},
clip width=0.5,
clip radius=1pt,
]
\strand[
red, double=red!20,
line width=0.4pt, double distance=0.7pt,
] (-1.5,1) to[out=90, in=-90] (-3,4)
    to[out=90, in=180, looseness=1] (-2,5)
    to(1.5,5)
    to[out=0,in=90, looseness=1] (2.5,4)
    to[out=-90, in=-90, looseness=2] (0.5,4)
    to[out=90, in=90, looseness=2.5] (-0.5,4)
    to[out=-90, in=-90, looseness=1.8] (3.25,4)
    to[out=90, in=90, looseness=1.5] (1,4)
    to[out=-90, in=-90, looseness=1.5] (-1.5,4)
    to[out=90, in=90, looseness=2] (-2.5,4)
    to[out=-90, in=-90, looseness=1.5] (1.5,4)
    to[out=90, in=90, looseness=1.5] (3,4)
    to[out=-90, in=-90, looseness=1.8] (-0.25,4)
    to[out=90, in=90, looseness=2] (0.25,4)
    to[out=-90, in=-90, looseness=2] (2.75,4)
    to[out=90, in=90, looseness=1.7] (-1,4)
    to[out=-90, in=180, looseness=1] (0,1.5)
    to[out=0, in=90, looseness=1] (1.5,1);
\end{knot}
\end{tikzpicture}

%\usepackage{amsmath}
%\usepackage{tikz}
%\usepackage{graphicx}
%\usetikzlibrary{knots}
%\usetikzlibrary{braids}

\begin{tikzpicture}
\pic[
braid/anchor=center,
ultra thick,
braid/strand 1/.style={red},
braid/strand 2/.style={green},
braid/strand 3/.style={blue},
braid/floor 1/.style={floor/.pic={\path[pic actions,draw=black,dashed,thin] (0,0) -- (1,0);}},
braid/floor 3/.style={floor/.pic={\path[pic actions,draw=black,dashed,thin] (0,0) -- (1,0);}},
braid/floor 5/.style={floor/.pic={\path[pic actions,draw=black,dashed,thin] (0,0) -- (1,0);}},
braid/floor 7/.style={floor/.pic={\path[pic actions,draw=black,dashed,thin] (0,0) -- (1,0);}},
name=coords,
] {braid={ |s_{1}s_{1}|s_{2}s_{2}|s_{1}^{-1}s_{1}^{-1}|s_{2}^{-1}s_{2}^{-1} }};
\node[at=(coords-1-s), pin=1] {};
\node[at=(coords-2-s), pin=2] {};
\node[at=(coords-3-s), pin=3] {};
\node[at=(coords-1-e), pin=south:1] {};
\node[at=(coords-2-e), pin=south:2] {};
\node[at=(coords-3-e), pin=south:3] {};
\node[at=(coords-1-0), pin=west:$a$] {};
\node[at=(coords-1-2), pin=west:$b$] {};
\node[at=(coords-1-4), pin=west:$a^{-1}$] {};
\node[at=(coords-1-6), pin=west:$b^{-1}$] {};
\end{tikzpicture}

%\usepackage{amsmath}
%\usepackage{tikz}
%\usepackage{graphicx}
%\usetikzlibrary{knots}
%\usetikzlibrary{braids}

\begin{tikzpicture}
\pic[
braid/anchor=center,
ultra thick,
braid/strand 1/.style={red},
braid/strand 2/.style={green},
braid/strand 3/.style={blue},
braid/floor 1/.style={floor/.pic={\path[pic actions,draw=black,dashed,thin] (0,0) -- (1,0);}}, 
name=ff
] {braid={ |s_{1}s_{1}}};
\node[at=(ff-1-s), pin=1] {};
\node[at=(ff-2-s), pin=2] {};
\node[at=(ff-1-e), pin=south:1] {};
\node[at=(ff-2-e), pin=south:2] {};
\node[at=(ff-1-0), pin=west:$a$] {};
\end{tikzpicture}
\begin{tikzpicture}
\pic[
braid/anchor=center,
ultra thick,
braid/strand 1/.style={red},
braid/strand 2/.style={green},
braid/strand 3/.style={blue},
braid/floor 1/.style={floor/.pic={\path[pic actions,draw=black,dashed,thin] (0,0) -- (1,0);}}, 
name=gg
] {braid={ |s_{1}^{-1}s_{1}^{-1}}};
\node[at=(gg-1-s), pin=1] {};
\node[at=(gg-2-s), pin=2] {};
\node[at=(gg-1-e), pin=south:1] {};
\node[at=(gg-2-e), pin=south:2] {};
\node[at=(gg-1-0), pin=west:$a^{-1}$] {};
\end{tikzpicture}

%\usepackage{amsmath}
%\usepackage{tikz}
%\usepackage{graphicx}
%\usetikzlibrary{knots}
%\usetikzlibrary{braids}

\begin{tikzpicture}
\begin{knot}[
clip width=4,
]
\strand [ultra thick, blue ] (1,0) circle (1.0cm);
\strand [ultra thick, red  ] (0,0) circle (1.0cm);
\strand [ultra thick, green] (0.5,1) circle (1.0cm);
\flipcrossings{3,4}
\end{knot}
\end{tikzpicture}

参考^Picture-Hanging Puzzles https://arxiv.org/pdf/1203.3602

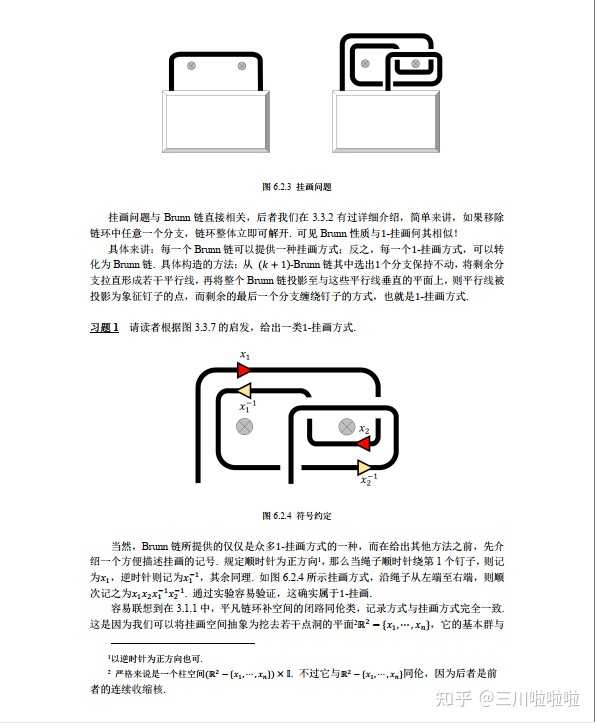
高赞回答已经很清楚了，基本上大家都会参考论文：
Demaine E D, Demaine M L, Minsky Y N, Mitchell J S B, Rivest R L, P?tra?cu M. Picture-Hanging Puzzles[J].
Picture-Hanging Puzzles
这篇论文插图很漂亮，欢迎大家观摩。
我自己也根据此文进行总结归纳——简单来说，这是一个构造单调布尔函数的问题，并且毫无意外，这是一个NP-C问题。
不过它和Brunn链的关系很大，详情见下文。

B站有个翻译过来的双语视频。就是关于这个问题的。
【如何使用数学来（非常垃圾滴）挂相框-哔哩哔哩】 https://b23.tv/xoat0Bj
从两个钉子一直扩展到任意数量的钉子。还给出了非常通俗的解法。(?′ω`? )

三个钉子合并沉重等于画框的重量，少一个钉子就掉。这算是一个工程师想法。还有其它方法：想象在3维中也有不同的感觉钉子形状以及位置的解法

从数学上看就是n-punctured plane X_n=\mathbb R^2-\{{x_1,\cdots,x_n}\} 里找一个非平凡的圈，使得它在n个嵌入 i_k:\mathbb R^2-\{x_1,\cdots,x_n\}\to \mathbb R^2-\{x_1,\cdots,\hat{x_k},\cdots,x_n\} 诱导的映射 (i_k)_*:\pi_1({X_n})\rightarrow \pi_1(X_{n-1}) 下平凡，这就转化成一个群论问题，也就是要寻找 \bigcap_{k=1}^n\text{ker}(i_k:*^{n}\mathbb Z\to *^{n-1}\mathbb Z) ,不过这个东西有什么好的描述吗？

[收藏本文] 【下载本文】

设计艺术最新文章

OpenAI Sora 生成 1 分钟视频时间超过 1 小

设计师的悲哀是什么？

加:2025-01-09 10:55:02 更:2025-01-09 11:13:09

股票涨跌实时统计涨停板选股分时图选股跌停板选股 K线图选股成交量选股均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

网站联系: qq:121756557 email:121756557@qq.com 天天财汇