| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 如何评价2024阿里巴巴数学竞赛预选赛试题? -> 正文阅读 |
|
|
[时尚穿搭]如何评价2024阿里巴巴数学竞赛预选赛试题? |
| [收藏本文] 【下载本文】 |
|
2024年阿里巴巴全球数学竞赛与2024年4月13日开始预选赛。 以下是本次试题 [图片] [图片] [图片] [图片] [图片] [图片] [图片]… |
|
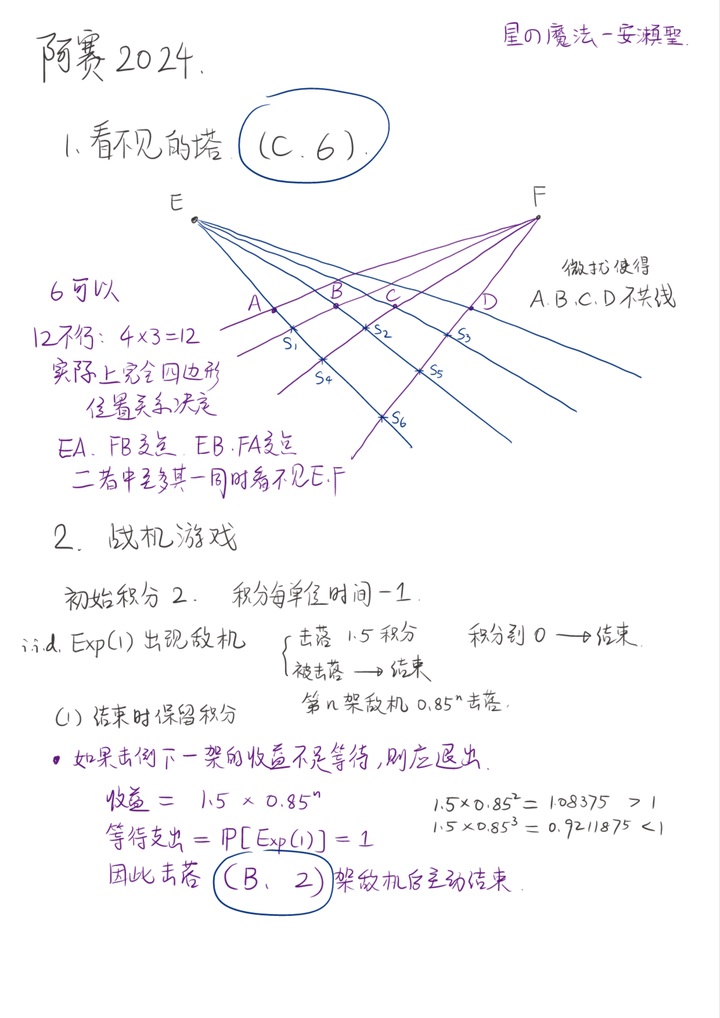
这次的初赛终于出了一些有点意思的题目,翻到最后可以看到我自己的答案。另外,我这个喵写数学证明的风格比较随手,和很多大佬不一样,我喜欢在写证明的时候保留脚手架,以便让人即便不看我的过程细节也能知道我在干什么。 总的来说,我认为这次的题目还是有一定难度,虽然很多问题本身叙述很高等,但是很多仍然可以通过巧妙的观察较为初等地解决。 另外,我很期待AI的表现。大胆预测一下AI能做对一个或两个选择(毕竟看起来比较好猜答案),然后大题就不好说了,要看它的知识库是否包含例如李代数表示具体的计算以及John椭圆的技巧,尤其是这里的中心对称情形(第四第五两题,不知道是否有文章具有直接的结论,如果没有的话AI仍然很难攻破。第三题的线性代数技巧太细,目前的transformer在数学问题上,很难给出完整严谨的证明,即便通过对语言模型做比较好的fine tune以及引导)。不过第六题应该是AI有希望做出来的。最后第七题AI可能难以写出对应距离的动力系统和映射,可能难以进行。 首先我们来简单观察一下每题都考察什么。 ☆第一题,看不见的塔,考察组合几何,通过分析完全四边形和直线上的序得到证明,例如对塔EF和AB,那么连线EA和FB交点以及EB和FA交点,二者至多其一是符合条件的,所以一下就能证出来是12/2=6。这个题目是这一类凸性分析的组合几何问题中最“轻量级”的,比较适合作为选择题。 ☆第二题,战机游戏,这个题考察的是连续时间的概率论和博弈论,尽管如果要严格地证明什么策略最优是数学上很困难的,但是通过某些“博弈常识”可以将问题变成例如函数和数列的最值。 其中第一小问可以完全离散地计算等待下一架敌机的得分期望。第二小问则较为困难,经过计算会发现这样一些“直觉”,例如:如果已经等了一会,敌机还没来,那么你应该一直等,否则早在当初“决定去等”的时候就要主动退出了。这不只是因为等的时间分数掉了是沉没成本,而且分数越少越应该“放手一搏”。 最后第二问的最优策略理应是,无论如何都等第一架敌机,打完后就跑,绝不等第二架,这样算出来准确概率是 \frac{17}8-\frac{17}{4e^2}\approx 2.07 。这也和上面的分析相符,最优策略一定是“很决绝”的。 ☆第三题,线性映射作用在平面格点的【稠密性】。这个题两问可以有不同的看法。在一开始考虑的时候,很自然地使用特征值来计算,但是这不够优美!聪明的办法是,注意第一问迹0的2阶矩阵,平方一定是数量矩阵,这意味着像格点的“形状”只有两种。第二问我们只需要用Minkowski找一个很短的像格点,然后A作用上去就能得到一个线性无关的格点(数论在这里发挥了作用),这时候二者生成了一个基本平行四边形(在椭圆曲线等理论中,大家也管它叫fundamental domain),这个平行四边形两条边长度都很短,所以它本身也很小。 实际上第三题之所以能这么做,我们观察失败的例子会更直观,例如为什么对角线上放1,2的矩阵(特征多项式是 (x-1)(x-2) 可约)为什么不行呢?因为它的幂次下1那一侧没有增长,导致它的四边形在一个方向被无限拉长,而如果它是一个二次数域的子格(甚至是order),那么你可以用复乘一个代数整数真的造出basis。 ☆第四题,一个看起来是线性代数具体计算的李代数表示论。这个题有两种攻克途径,对于数学物理学家来说,暴力计算找规律绝对是重要的研究手段,所以我一上来就写了一个mathematica代码来计算。但是同时,在看到题的一瞬间,这些系数应该使你隐隐约约感受到sl2表示的味道。于是计算的辅助下,你发现换元vi乘某个阶乘竟然能将它们直接对应sl2的2d+1维的齐次多项式表示! X=\left[\begin{matrix}0&1\\0&0\end{matrix}\right],\ Y=\left[\begin{matrix}0&0\\1&0\end{matrix}\right],\ H=\left[\begin{matrix}1&0\\0&-1\end{matrix}\right]. 那么这时候你就只需要“构造字典”,就是把题目中的语言完全转化为sl2表示里的语言,首先是它的f,对应sl2表示的 (X+Y)/2 ,所以是半单元,它的特征值是标准的 H 的一半,一个小技巧是注意到半单李代数的Cartan子代数都是共轭的,所以其中的半单元可以通过内自同构变过去,所以特征值就是一半,而 2d+1 维表示的标准H特征值我们熟知是 -2d,-2d+2,\cdots,2d ,所以这里的f就具有一半的 -d,-d+1,\cdots,d 就是如同题目要求那样的特征值。这个内自同构甚至是一个对合,相当于李群SL2中元素 \frac1{\sqrt 2}\left[\begin{matrix}1&1\\-1&1\end{matrix}\right] 的共轭作用,可以具体写出来,它就是 X\mapsto \frac12(H-X+Y),\ Y\mapsto \frac12(H+X-Y),\ H\mapsto X+Y. 剩下两个小问就是具体去算,然后找更多的规律了…我不知道有没有更多表示论背景,反正我是硬来的,知道背景的小可爱可以说一声。 ☆第五题,本题是真正的组合几何与凸优化。首先要知道小学二年级就学过的,John 椭球的背景知识,不知道的小可爱们可以上wiki什么的搜一下。大概就是说,对于欧氏空间的一个有界凸集,存在唯一最小体积的外接椭球(这个椭球其实把凸集包裹得很好,很容易猜测它就是符合条件的解),但是有的小伙伴会说,不对啊,题目要求的是面积最小啊?这里就是这个问题特有的技术细节了。 对于中心对称的凸集 V ,利用John椭球的唯一性,我们其实可以证明出来John椭球 E 也得是中心对称的,然后接下来的技巧大概就是证明这个椭球的 1/\sqrt 3 倍实则内含(可以有切点)于凸集 V ,以及三角不等式的高维推广,得到包含的凸集其表面积也具有不等式关系。所以 A(E)\ge A(V)\ge A(E/\sqrt 3)=A(E)/3. 这里 A 表示表面积。实际上通过一些观察把问题化归为中心对称凸八面体的情况,可以证明 3 可以被换成更优的常数 \pi/\sqrt 3 ,这也是正八面体时的比值 A(外接球)/A(正八面体) 。 ☆第六题,本题的背景是生成函数/Fourier变换/有限状态Markov过程。相比前面的问题来说,这个问题绝对是最友好的一道题,简单来说,我们应该指望最后的奇偶性应该是充分均匀的,在样本数很大的时候我们应该不大能得到什么奇偶信息。 那么证明这种结论的技巧有几种,首先最容易想的办法就是直接算,实际上因为是独立的Bernoulli分布,它的生成函数是极其容易求出来的,在此之后,计算奇偶无非就是代入 \pm1 然后取平均,一个硬币是取 1/2 的平均,本质上说一个硬币其实可以看作两个福,一个【正面福】和一个【反面福】。而对于多个福的情况,生成函数无非是多几个变量,往里代 \pm 1 的技巧是完全一样的。 再说说Markov过程的办法,实际上有这样一个结果,就是一个状态集的有限子集 S ,如果它是【封闭的】,也就是说从它出发到它外面的概率是 0 ,而且它是【可迁的】,也就是说这个子集中任意两个状态间都有正的转移概率,那么从该子集开始者,最后一定会趋于稳定分布,落在每个状态的概率都是均匀的 1/|S| 。 利用这个结果,那么抛硬币就是两个状态,正面总量奇数和偶数。收集五福则要注意一下,因为题目问的是 2n 次抽取的极限,所以相当于一次开两个福。所以在总共奇偶的 2^5=32 种可能中恰好只有一半的情况是总量全为偶数的,剩下一半情况都是不会出现的,所以 |S|=16 ,于是最后的全偶概率就是 1/16 。 ☆第七题,本题的背景是微分动力系统。只要写出来当前二人距离,到两个人各经过一次树下后新距离的函数,就会发现第一问的情况是,距离有一个不动点 d_0 ,然后距离 d>d_0 就会不断变大,因为圆周长是 1 所以最后距离变成 0,1 都算是两人相遇。 第二问懒得做了,摆烂了!!!实际上我在周日出去玩儿了,所以也没算最后一小问。粗看上去无非就像 x_{n+1}=\sin x_n 那道经典淑芬习题一样,只需要估个阶就完了,所以也不是很有兴趣和动力去做。 附上我的解答。 |
|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
做完了,然后感觉很离谱 一句话就是,抽象但简单。从来没有哪次初赛像这一次我都能做出来。答案在文末。 首先评价一下题目 第一题不说了 第二题不想算,直接拿计算机模拟 第三题我只能说抽象,他题目也没说C是不是绝对常数,但是我想了一下,他不可能是绝对常数于是不管了。只要意识到其实我们是在给最短距离的下界就没啥好说。 第四题是真抽象,算特征方程算了好久,后来干脆直接去找特征向量算了。然后注意到d的特征向量是常数,d-1是一次函数,d-2的就尝试插了个值是二次函数,后面这个题就可以了。听别人说是什么Sylvester-Kac矩阵,不知道。 第五题就是John ellipsoid。。。我觉得直接搬这篇作答有点op了,于是相当于我把他用我的语言重新说了一遍。最后“两个凸体,一个包含另外一个,那么在外面的比在里面的表面积大”我没证明,就是熟知结论。 第六题差不多离散傅立叶变换,不说了,老本行。 第七题写了这么一大堆,其实就是个函数迭代的事情。然后本来在想啊这个分析这方面我该怎么办?结果一看,好家伙在实数上光滑,那没事了。我只想着今年第七题拉了,以前的第七题那种应用数学的都是像什么pde呀,或者是各种什么鬼系统的,完全做不来的那种。 接下来开始骂了。 首先有几个题这个题意是有点离谱,你一个数学考试我还得揣测出题人的意图。 前面说了你第三题这个常数,然后在另一个群里看到第二题还有别的理解方式。之后更恶心的是第七题这么长,真就增加阅读量呗。而且最后一题你初值都不给,你最后的次数答案明显和初值到不动点的距离有关,你问我什么数量级?于是我到底该不该给出一个答案它包括初值? 然后其次这次题目是真的抽象。第二题我真的相信没有什么能够手算的方法,那说句实话,我觉得这就有点歧视不会编程的人了。真的其实今年选择题就这么点,以往挺多的。(后来评论区有人说可以手算,好的,果然是我太菜了。) 第七题他恶就恶心在你把各种什么东西一剥离出来,他就是个函数迭代问题,真的考数学,顺道把语文阅读理解也考了呗? 第五题我真的想说不知道John ellipsoid你还真的不知道有没有第二个证明办法了(可能是我是个傻子,不会做),就纯纯的论文。 第四题我都不知道他为啥要给你这么一个换元的障眼法。我不知道那个障眼法的意义在哪里。拜托,两天时间诶,做出来就能做出来,做不出来就是做不出来,障眼法设的有什么意义呢。起不到增加本质性难度的作用,拖时间也拖不了多长的时间。 顺便po下我的答案(考场的答案直接复制粘贴整理的) C(1)B (2)A |

|
|
|

|
|
|

|
|
4. |

|
|
|

|
|
5. |

|
|
|

|
|
6. |

|
|
|

|
|
7. |

|
|
|

|
|
|
|
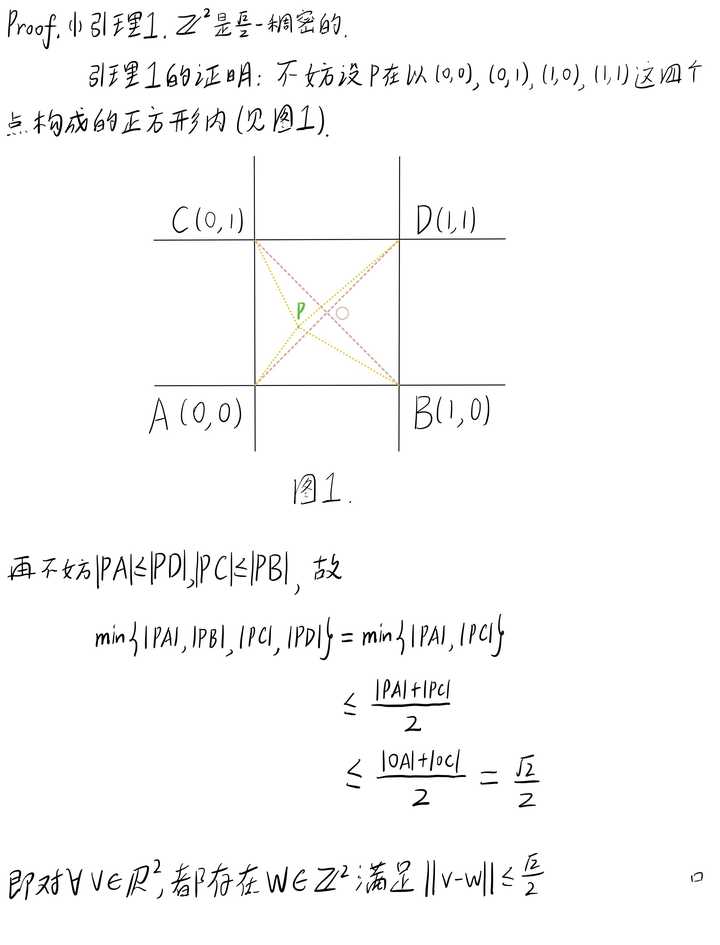
总结:至多错了个5分的选择和5分的大题,这把至少110分问题1 Proof.答案至多是组合数 {4\choose 2} ,又因为可以构造出最大的情况,所以是6,选C. 问题2(1) 直接写程序 根据模拟结果,小明在击落第2架敌机后退出游戏可以期望获得最大的积分,其数学期望大约为2.35分。因此,为了最大化游戏结束时的累积积分,小明应该选择在击落第二架敌机后主动结束游戏。所以正确答案是选项 B.2 问题2(2) 这题没太懂题目,继续写程序 跑出来是6,所以猜了个C. 问题3 这题第二问的第二种情况做了17h也没做出来啊啊啊啊...... |
|
|
|

|
|
|

|
|
|

|
|
|

|
|
问题4 高等代数竞赛题 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
问题5 这题背景肯定是L?wner-John ellipsoid,但是原定理的结论没法解决原题,最多只能把系数做到9而不是3,所以还需要再结合题目里的中心对称性改进定理证明: |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
问题6 |

|
|
|

|
|
|

|
|
|
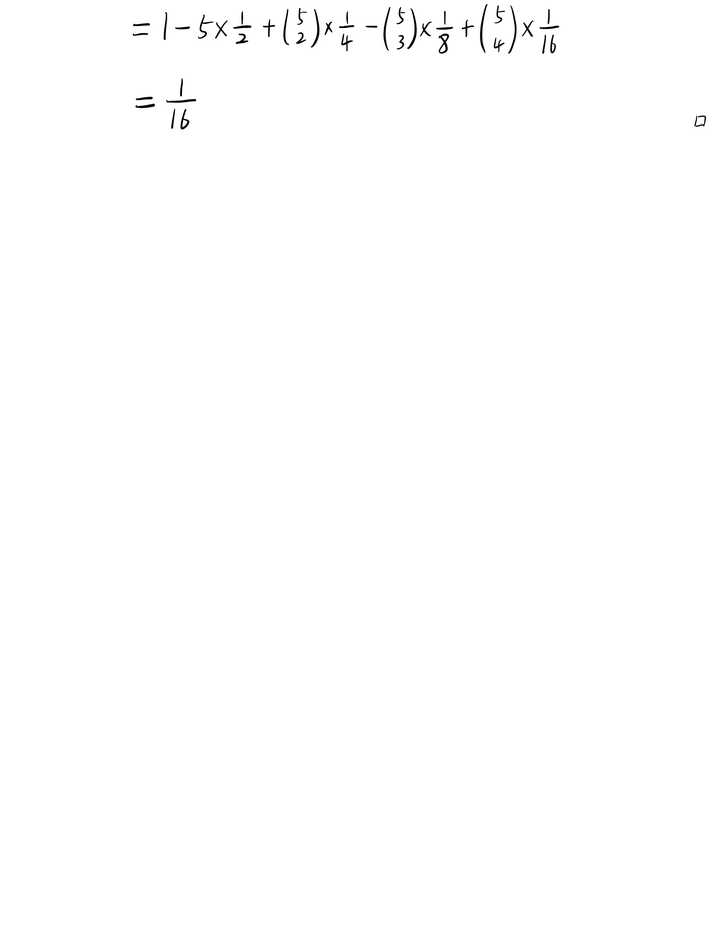
|
|
问题7 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
知乎首答献给阿赛喵~ |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
|
做了三个选择,第一道高代第一问,第二道高代全部小问,还有一个概率论大题,总共70分 第五题第七题没做,查了一下五还是论文题,不会。 七如果翻译成大一数分题我还会想一想,如果要我自己建模和翻译的话......我懒,不想做,不喜欢这种实际应用问题,题干还那么长( 概率论是纯送分啊,不会做鉴定为:没上过高中? |

|
|
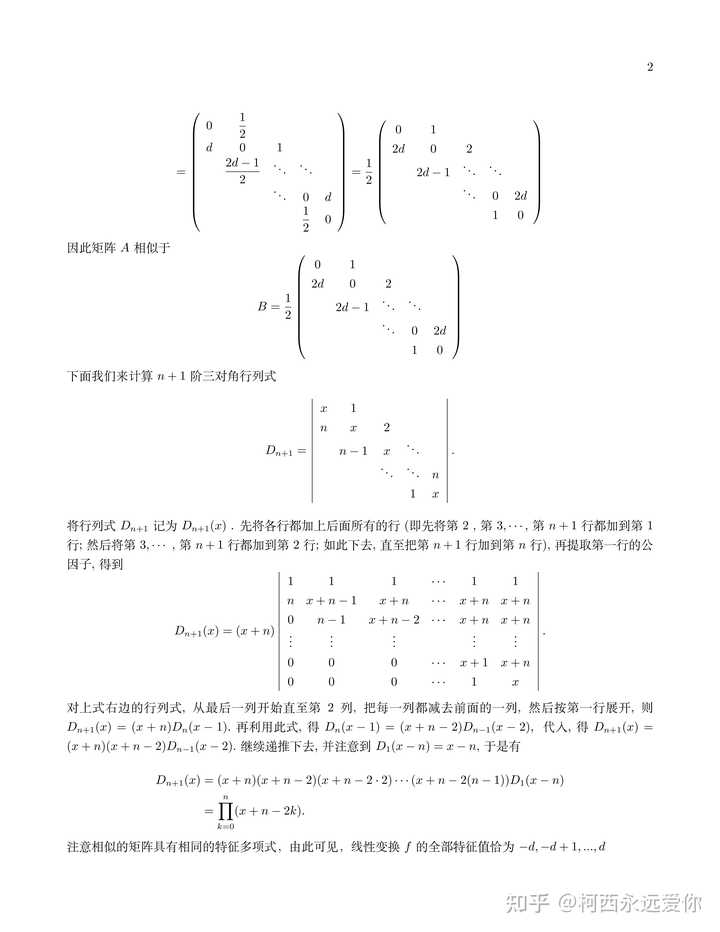
然后来说高代,这次的高代题目出的相当有难度,我也想了挺久的,就当做CMC高等代数考前模拟题了这是高代第二题 |

|
|
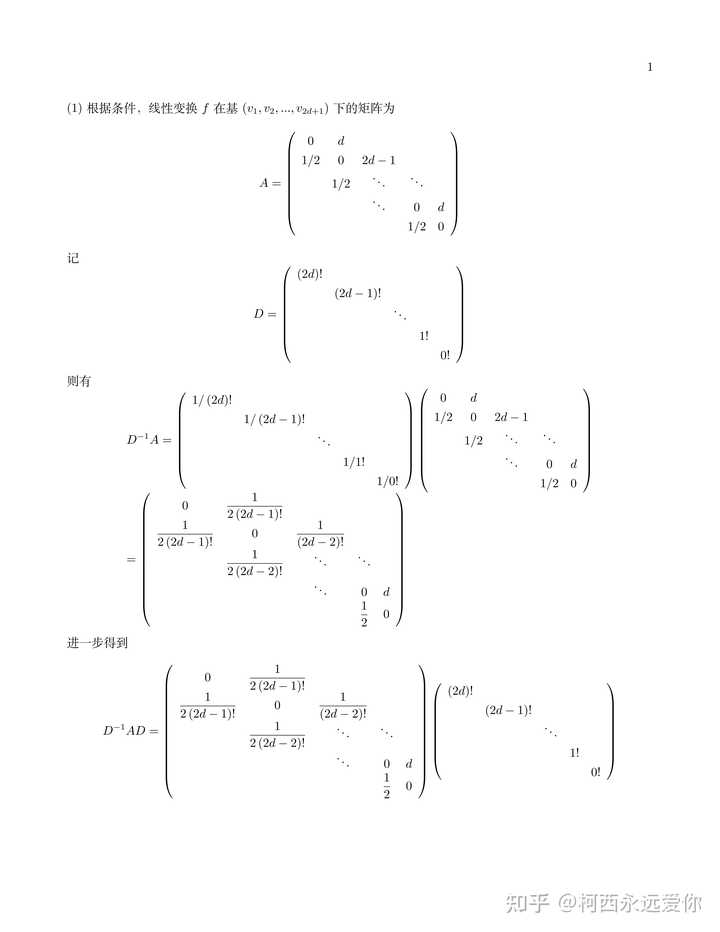
从第一问开始就很难算,后面两问找规律先猜后证更是麻烦的要死,不过我还是采用纯线性代数方法硬撸出来了 |
|
|
|
|
|
|

|
|
|

|
|
|

|
|
听群里一些大佬说有抽象代数还是表示论的方法?咱没学过这些奇奇怪怪的东西,不做评价,我还是喜欢用初等方法解决问题 第一道高代题有两问,第一问不难而且非常直观,因为本质上一般的幂次就是0,1这两种情况,画个图基本就做出来了 |

|
|
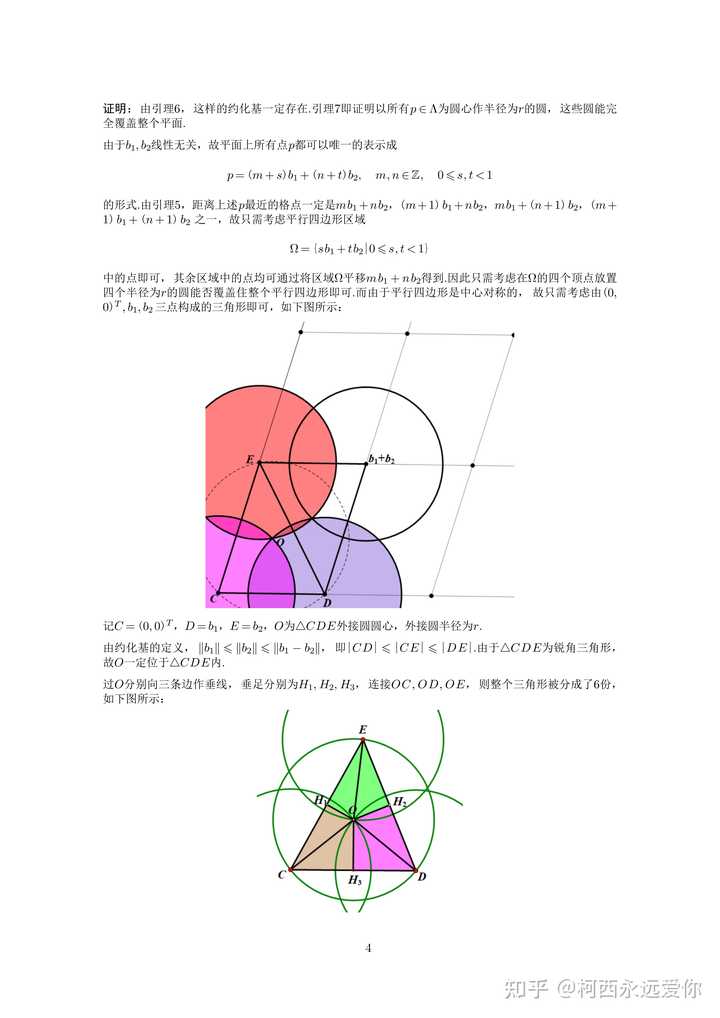
第二问与其说是高等代数不如说是数论/组合问题,与密码学关系紧密,不过似乎多项式不可约这个条件是多余的!只要矩阵可逆就行,搬运一个大佬的解答 |

|
|
|

|
|
|

|
|
|

|
|
|
|
|
|
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |