| |
|
|
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 自然科学 -> 世界上收敛最快的计算 π 的公式是什么？ -> 正文阅读 |
|
|
[自然科学]世界上收敛最快的计算 π 的公式是什么？ |
| [收藏本文] 【下载本文】 |
|
如题 |
|
1.拉马努金公式，即 1π=89801∑n=0∞(4n)!(1103+26390n)(n!)43964n" role="presentation">1π=89801∑n=0∞(4n)!(1103+26390n)(n!)43964n\frac{1}{\pi}=\frac{\sqrt{8}}{9801}\sum_{n=0}^{\infty}{\frac{(4n)!(1103+26390n)}{(n!)^{4}396^{4n}}} 2.博温兄弟的迭代方法 yn+1=1−(1−yn4)1/41+(1−yn4)1/4" role="presentation">yn+1=1?(1?yn4)1/41+(1?yn4)1/4y_{n+1}=\frac{1-(1-y_{n}^{4})^{1/4}}{1+(1-y_{n}^{4})^{1/4}} αn+1=(1+yn+1)4αn−22n+3yn+1(1+yn+1+yn+12)" role="presentation">αn+1=(1+yn+1)4αn?22n+3yn+1(1+yn+1+yn+12)\alpha_{n+1}=(1+y_{n+1})^{4}\alpha_{n}-2^{2n+3}y_{n+1}(1+y_{n+1}+y_{n+1}^{2}) 其初值 y0=2−1,α0=6−42" role="presentation">y0=2?1,α0=6?42y_0=\sqrt{2}-1,\alpha_{0}=6-4\sqrt{2} ，有 limn→∞1αn=π" role="presentation">limn→∞1αn=π\lim_{n \rightarrow \infty}{\frac{1}{\alpha_n}}=\pi -------更新------- 3.丘德诺夫斯基公式 拉马努金公式的改良版 π=42688010005∑n=0∞(6n)!(13591409+545140134n)(3n)!(n!)3(−640320)3n" role="presentation">π=42688010005∑n=0∞(6n)!(13591409+545140134n)(3n)!(n!)3(?640320)3n\pi=\frac{426880\sqrt{10005}}{\sum_{n=0}^{\infty}{\frac{(6n)!(13591409+545140134n)}{(3n)!(n!)^3(-640320)^{3n}}}} |
|
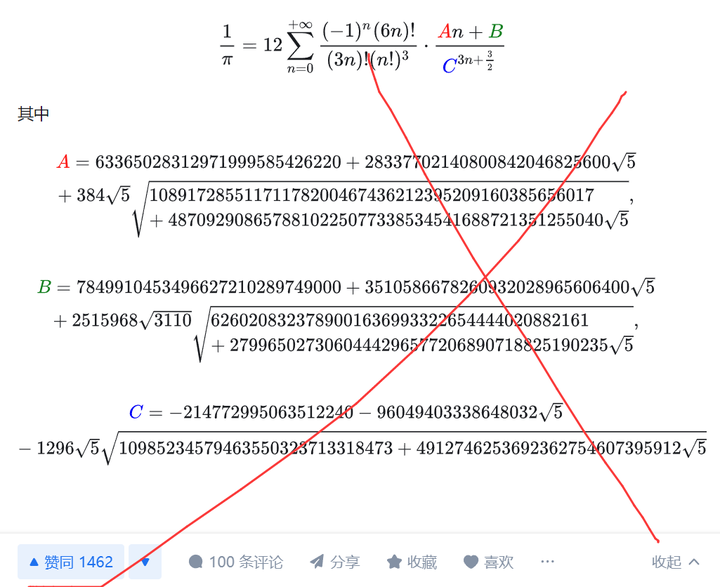
1π=∑n=0+∞(6n)!(3n)!(n!)3⋅A+BnC3n⋅−C3" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">1π=∑n=0+∞(6n)!(3n)!(n!)3?A+BnC3n??C3\frac{1}{\pi}=\sum_{n=0}^{+\infty} \frac{(6 n) !}{(3 n) !(n !)^3} \cdot \frac{{\color{red}A}+{\color{green}B}n}{{\color{blue}C}^{3n}\cdot \sqrt{{-{\color{blue}C}}^3}}\\ 其中 A=63365028312971999585426220+283377021408008420468256005+384510891728551171178200467436212395209160385656017+48709290865788102250773385345416887213512550405,  B=7849910453496627210289749000+35105866782609320289656064005+251596831106260208323789001636993322654444020882161+27996502730604442965772068907188251902355,  C=−214772995063512240−960494033386480325−1296510985234579463550323713318473+49127462536923627546073959125" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">A=63365028312971999585426220+283377021408008420468256005+384510891728551171178200467436212395209160385656017+48709290865788102250773385345416887213512550405, B=7849910453496627210289749000+35105866782609320289656064005+251596831106260208323789001636993322654444020882161+27996502730604442965772068907188251902355, C=?214772995063512240?960494033386480325?1296510985234579463550323713318473+49127462536923627546073959125\color{red}{A}=63365028312971999585426220+28337702140800842046825600\sqrt{5}+384\sqrt{5}\sqrt{10891728551171178200467436212395209160385656017 + 4870929086578810225077338534541688721351255040\sqrt{5}},\\ \space\\ \space\\ \color{green}{B} = 7849910453496627210289749000+3510586678260932028965606400\sqrt{5}+ 2515968\sqrt{3110}\sqrt{6260208323789001636993322654444020882161+ 2799650273060444296577206890718825190235\sqrt{5}},\\ \space\\ \space\\ \color{blue}{C}=?214772995063512240? 96049403338648032\sqrt{5} ? 1296\sqrt{5}\sqrt{10985234579463550323713318473 + 4912746253692362754607395912\sqrt{5}}\\ 拉马努金公式是一个系列, 这是其中之一. 因为知乎不支持旋转90度写公式, 所以一页实在是放不下, 把三个写起来很长的常数分开写了. 该级数每算一个 n" role="presentation">nn , π" role="presentation">π\pi 的有效位数大约增加 50 位. 收敛速度嘎嘎的 关于一些问题....... 问: 这个公式收敛速度快, 但是算起来不一定快啊? 答: 题目问的啥? 另外, 因为三个常数在公式里不变, 所以可以先算出来这三个常数, 然后后面就可以直接用了, 没必要每次都算一遍对吧. 问: 三个常数好算吗? 答: 使用程序还是比较好算的. 比如Mathematica, 可以求解到任意精度. 问: 这个公式中的三个常数似乎是错的? 答: 你看的真够仔细......首先这个公式中的ABC可以有三组解, 我这里列出来的是收敛最快的那一组, 所以应该是没错的. 另外两组分别是 A=545140134,B=13591409,C=640320," role="presentation" style="font-size: 100%; display: inline-block; position: relative;">A=545140134,B=13591409,C=640320,A = 545140134, \\B = 13591409, \\C = 640320,\\ 和 A=1657145277365+21217571091261,B=107578229802750+1377398089267261,C=5280(236674+3030361)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">A=1657145277365+21217571091261,B=107578229802750+1377398089267261,C=5280(236674+3030361)A = 1657145277365 + 212175710912\sqrt{ 61},\\ B = 107578229802750 + 13773980892672\sqrt{61},\\ C = 5280(236674 + 30303\sqrt{61})\\他们的收敛速度分别是, 每多算一个项目, 有效位数分别大约增加 14 位, 31 位. 不过这两个常数对应的公式是不同的, 根据答主 @hqztrue 找到的这个网站: Borwein's algorithm | Detailed Pedia?www.detailedpedia.com/wiki-Borwein%27s_algorithm 可以查到细节. 其实利用代数数论和二次域的知识还可以构造出更多这样的拉马努金型公式. 问: 可是你罗列的参数确实是错的? 答: 那就是复制粘贴错了. 我更好奇的是真的有人一位一位的去演算吗? 厉害! 不过更有趣的事情是了解这些公式的来源方法, 通过怎样的思路去推导出来这些公式, 它们的机理是什么. 我们应该重点关心这些. 此处得感谢答主 @hqztrue 真的去验证了一下并且找到了一个错误. 是我疏忽了, 不过我确实一开始没想到这个公式会有人去验证, 因为本质上是展示类似构造的公式, 在此处对由于侥幸心理疏忽导致的错误道歉, 这种不仔细可能会误导一些人在后续的工作上产生错误的影响, 我将避免犯该类错误. 对于该答主于该公式上的编程性能验证, 在此也表示感谢. 可以于该回答中查看 世界上收敛最快的计算 π 的公式是什么？271 赞同 · 31 评论回答 |
|
|
一些其他的算法: 例如: 优美的BBP公式的推导思路如下 (BBP公式可以求解十六进制下π的小数点后任意位, 而无需事先求解其前面的小数位数. 同时在甚至16位支持浮点数的处理器上都能运行该算法). π的BBP公式之一如下: π=∑i=0∞116i(48i+1−28i+4−18i+5−18i+6)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">π=∑i=0∞116i(48i+1?28i+4?18i+5?18i+6)\begin{align} \pi=\sum_{i=0}^{\infty}{\frac1 {16^i}}(\frac4 {8i+1}-\frac2 {8i+4}-\frac1 {8i+5}-\frac1 {8i+6}) \end{align}\\ 证明: 首先有∑i=0∞116i(8i+n)=2n∑i=0∞∫012x8i+n−1dx=2n∫012xn−11−x8dx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">∑i=0∞116i(8i+n)=2n∑i=0∞∫012x8i+n?1dx=2n∫012xn?11?x8dx \begin{align} \sum_{i=0}^{\infty}{\frac1{16^i(8i+n)}}=\sqrt{2}^n\sum_{i=0}^{\infty}{\int_{0}^{\frac1{\sqrt{2}}}x^{8i+n-1}dx}=\sqrt{2}^n\int_{0}^{\frac1{\sqrt{2}}}\frac{x^{n-1}}{1-x^8}dx \end{align}\\ 则∑i=0∞116i(48i+1−28i+4−18i+5−18i+6)=∫01242−8x3−42x4−8x51−x8dx" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">∑i=0∞116i(48i+1?28i+4?18i+5?18i+6)=∫01242?8x3?42x4?8x51?x8dx \begin{align}\sum_{i=0}^{\infty}{\frac1 {16^i}}(\frac4 {8i+1}-\frac2 {8i+4}-\frac1 {8i+5}-\frac1 {8i+6})=\int_{0}^{\frac1{\sqrt{2}}}\frac{4\sqrt{2}-8x^3-4\sqrt{2}x^4-8x^5}{1-x^8}dx\end{align}\\ 替换得∫0116y−16y4−2y3+4y−4dy=π" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">∫0116y?16y4?2y3+4y?4dy=π\begin{align}\int_{0}^{1}\frac{16y-16} {y^4-2y^3+4y-4}dy=\pi\end{align}\\ 证毕. 给整个公式乘上 16k" role="presentation">16k16^k 即可直接求得十六进制下第 k" role="presentation">kk 位小数的值. 如果不考虑数学上的收敛速度的话, 只是希望尽快算出答案的话, 这个公式其实更好一些. 因为它天生是分布式的. (当然上面的拉马努金公式也是分布式的, 但是对于计算机来说存在精度问题, 计算机不容易处理小数). 而且BBP公式对于求解例如"π的小数点后一百万亿位的十六进制/二进制是什么?"这类问题显然很容易, 手算都行. |
|
Chudnovsky公式： 1π=153360640320∑n=0∞(−1)n(6n)!(n!)3(3n)!13591409+545140134n6403203n" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">1π=153360640320∑n=0∞(?1)n(6n)!(n!)3(3n)!13591409+545140134n6403203n\frac{1}{\pi}=\frac{1}{53360\sqrt{640320}}\sum_{n=0}^{\infty}(-1)^n\frac{(6n)!}{(n!)^3(3n)!}\frac{13591409+545140134n}{640320^{3n}}\\ |
|
楼上给的算法全是错的，充满了 YY. |
|
|
但凡自己编程试下，就会发现不可能算到一万位, 更别说一万亿位了. 首先你这堆根号套根号, 你怎么控制精度? 记住每开一次根号, 精度减半 然后就是一堆阶乘, 你自己算算展开 100 项是多少位的数字除多少位的数字. 这堆东西全部乘起来你再加起来还能保留有效精度就有鬼了.... 不止这个答案, 其他所有用级数一项一项加起来, 里面还含有阶乘的答案, 全部都是错的 正确做法 考虑如下一级拉马努金级数(Level-1 Ramanujan Series): 1π=∑k=0∞(−1)k+1(2kk)(3kk)(6k3k)c−k−12(ak+b)" role="presentation">1π=∑k=0∞(?1)k+1(2kk)(3kk)(6k3k)c?k?12(ak+b)\displaystyle \frac{1}{\pi }=\sum_{k=0}^∞(-1)^{k+1}\binom{2 k}{k} \binom{3 k}{k} \binom{6 k}{3 k}c^{-k-\frac{1}{2}} (a k+b) 其中 a,b,c" role="presentation">a,b,ca, b, c 是三个未知整数, j" role="presentation">jj 函数定义如下, 也是个整数 c=j(1+−τ2)j(τ)=(E4(τ)η8(τ))3=1q+744+196884q+21493760q2+⋯" role="presentation">c=j(1+?τ2)j(τ)=(E4(τ)η8(τ))3=1q+744+196884q+21493760q2+? \begin{aligned} c &= j\left(\frac{1+\sqrt{-τ}}{2}\right)\\ j(τ)&=\left({\frac {E_{4}(\tau )}{η^{8}(τ)}}\right)^{3}={\frac {1}{q}}+744+196884q+21493760q^{2}+\cdots \end{aligned} 选取如下参数 {a=163×40133016b=163096908τ=163c=6403203" role="presentation">{a=163×40133016b=163096908τ=163c=6403203 \left\{ \begin{aligned} a &= 163×40133016 \\ b &= 163096908 \\ τ &= 163\\ c &= 640320^3\\ \end{aligned} \right. 可以看到没有任何根号, 都是精确的数字. 接着想办法解决一大堆阶乘求和的精度问题. 令 f(k)=(−1)k+1(2kk)(3kk)(6k3k)c−k" role="presentation">f(k)=(?1)k+1(2kk)(3kk)(6k3k)c?k\displaystyle f(k)=(-1)^{k+1}\binom{2 k}{k} \binom{3 k}{k} \binom{6 k}{3 k} c^{-k} 注意到两式之比可以表达成: f(n)f(n−1)=8c(6n−1)(6n−3)(6n−5)n3" role="presentation">f(n)f(n?1)=8c(6n?1)(6n?3)(6n?5)n3\displaystyle \frac{f(n)}{f(n-1)}=\frac{8}{c}\frac{(6 n-1) (6 n-3) (6 n-5)}{n^3} 于是有 1π=c−12(b+∑k=1∞∏n=1k(8c×(6n−1)(6n−3)(6n−5)n3)(ak+b))" role="presentation">1π=c?12(b+∑k=1∞∏n=1k(8c×(6n?1)(6n?3)(6n?5)n3)(ak+b)) \begin{aligned} \frac{1}{π} =c^{-\frac{1}{2}}\left(b+\sum_{k=1}^∞\prod_{n=1}^k\left(\frac{8}{c}×\frac{(6 n-1) (6 n-3) (6 n-5)}{n^3}\right) (a k+b)\right) \end{aligned} 又令: P(p,q)=∏j=pq−1(6j−1)(6j−3)(6j−5)Q(p,q)=∏j=pq−1c×(j2)3S(p,q)=∑k=pq−1P(p,k+1)Q(p,k+1)(ak+b)R(p,q)=Q(p,q)S(p,q)" role="presentation">P(p,q)=∏j=pq?1(6j?1)(6j?3)(6j?5)Q(p,q)=∏j=pq?1c×(j2)3S(p,q)=∑k=pq?1P(p,k+1)Q(p,k+1)(ak+b)R(p,q)=Q(p,q)S(p,q) \begin{aligned} P(p,q)&=\prod_{j=p}^{q-1}(6 j-1) (6 j-3) (6 j-5)\\ Q(p,q)&=\prod_{j=p}^{q-1}c× \left(\frac{j}{2}\right)^3 \\ S(p,q)&=\sum_{k=p}^{q-1}\frac{P(p,k+1)}{Q(p,k+1)}(a k+b)\\ R(p,q)&=Q(p,q) S(p,q)\\ \end{aligned} 以上可以重写为递推定义: P(p,q)=P(p,r)×P(r,q)Q(p,q)=Q(p,r)×Q(r,q)S(p,q)=S(p,r)+P(p,r)Q(p,r)S(r,q)R(p,q)=Q(r,q)R(p,r)+P(p,r)R(r,q)" role="presentation">P(p,q)=P(p,r)×P(r,q)Q(p,q)=Q(p,r)×Q(r,q)S(p,q)=S(p,r)+P(p,r)Q(p,r)S(r,q)R(p,q)=Q(r,q)R(p,r)+P(p,r)R(r,q) \begin{aligned} P(p,q)&=P(p,r)×P(r,q)\\ Q(p,q)&=Q(p,r)×Q(r,q)\\ S(p,q)&=S(p,r)+\frac{P(p,r)}{Q(p,r)}S(r,q)\\ R(p,q)&=Q(r,q)R(p,r) + P(p,r)R(r,q)\\ \end{aligned} 边界条件为: P(p,p+1)=(6p−1)(6p−3)(6p−5)Q(p,p+1)=cp38S(p,p+1)=P(p,p+1)Q(p,p+1)(ap+b)R(p,p+1)=P(p,p+1)(ap+b)" role="presentation">P(p,p+1)=(6p?1)(6p?3)(6p?5)Q(p,p+1)=cp38S(p,p+1)=P(p,p+1)Q(p,p+1)(ap+b)R(p,p+1)=P(p,p+1)(ap+b) \begin{aligned} P(p,p+1)&=(6p-1)(6p-3)(6p-5)\\ Q(p,p+1)&=\frac{cp^3}{8}\\ S(p,p+1)&=\frac{P(p,p+1)}{Q(p,p+1)}(a p + b)\\ R(p,p+1)&=P(p,p+1)(a p + b)\\ \end{aligned} 这里所有出现的数字都是整数, 这个才是可编程计算的无精度损失版本. 把 S 的表达式代入原式有: \displaystyle \frac{1}{π}=c^{-\frac{1}{2}}\left(b+S(1,∞)\right) 翻个身 π=\dfrac{\sqrt{c}}{b+S(1,∞)} 当然计算机没法算到无穷 直接截断即可, 对于 t = 163 就是: π≈\dfrac{5122560\sqrt{10005}}{163096908+S(1,n)} 每一轮是增加 14.19 位十进制精度 一般编程计算的是这个公式才对. 但是如果你去看 chudnovsky.c 源码, 会发现用的并不是这套参数 这是因为 \mathrm{GCD}(163 × 40133016, 163096908) = 12 所有参数可以约去 12, 于是有: π≈\dfrac{426880\sqrt{10005}}{13591409+S(1,n)} 这个就是超级计算机上跑的能算一万亿的版本了. 当然你这个迭代得超级计算机上分块计算, 单机没法算. 这里给出了其他 τ 值对应的参数, 一共有 7 个这种参数组, 但是只有 3 个用迭代法计算 |
|
这个应该是你需要的，以后提问时请先善用搜索功能。 |
|
|
| [收藏本文] 【下载本文】 |
| 自然科学 最新文章 |
| 海南一村民被眼镜王蛇咬死，多名消防员和村 |
| 有哪些不起眼的牢底坐穿兽？ |
| 美国耕地面积比中国大，可为什么粮食产量不 |
| 如何看待同济大学2024国家科技三大奖颗粒无 |
| 假如航母被蓝鲸全速前进撞一下会怎么样？ |
| 你见过最狠的SCI评论是什么? |
| 你在实验室最惊险的瞬间是什么？ |
| 牛顿生活在中国，会有什么成就？ |
| 虎鲸为什么不吃人？ |
| 数学为什么这么可笑？ |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |