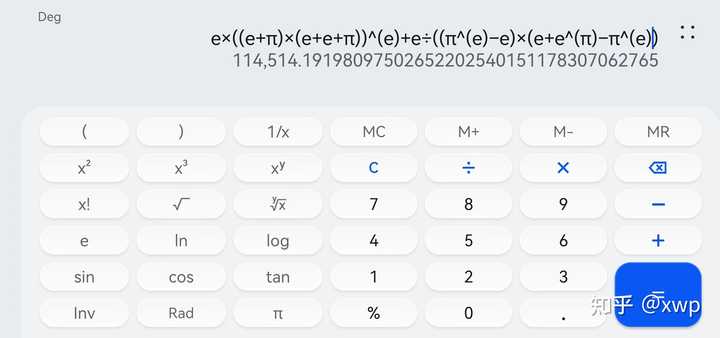
不要说这种精度很低的
   π4+π5−e6" role="presentation"> π4+π5?e6~~~\pi^4+\pi^5-e^6≈−0.00001767345123210920." role="presentation">≈?0.00001767345123210920.\approx -0.00001767345123210920.
下面这些高精度的
   π−(2−22−24)2" role="presentation"> π?(2?22?24)2~~~\pi-\left( \frac{2-\sqrt{2\sqrt{2}-2}}{4} \right)^2 ≈−0.00000432058238," role="presentation">≈?0.00000432058238,\approx-0.00000432058238,
   π−883−218" role="presentation"> π?883?218~~~\pi-\frac{\sqrt{883}-\sqrt{21}}{8} ≈0.000000125933366815771," role="presentation">≈0.000000125933366815771,\approx0.000000125933366815771,
   π−12564839995" role="presentation"> π?12564839995~~~\pi-\frac{125648}{39995}≈−0.0000000454975926847777," role="presentation">≈?0.0000000454975926847777,\approx-0.0000000454975926847777,
   π−2143224" role="presentation"> π?2143224~~~\pi-\sqrt[4]{\frac{2143}{22}} ≈0.00000000100714711325660," role="presentation">≈0.00000000100714711325660,\approx0.00000000100714711325660,
   π−2865814615" role="presentation"> π?2865814615~~~\pi-\sqrt[15]{28658146} ≈−0.00000000022371868," role="presentation">≈?0.00000000022371868,\approx-0.00000000022371868,
   π−88858240318" role="presentation"> π?88858240318~~~ \pi-\sqrt[18]{888582403} ≈0.00000000001399735," role="presentation">≈0.00000000001399735,\approx0.00000000001399735,
   π−876995679620" role="presentation"> π?876995679620~~~\pi-\sqrt[20]{8769956796} ≈0.0000000000014812," role="presentation">≈0.0000000000014812,\approx0.0000000000014812,
   π−16570706552746197" role="presentation"> π?16570706552746197~~~\pi-\frac{165707065}{52746197} ≈−0.0000000000000001640." role="presentation">≈?0.0000000000000001640.\approx-0.0000000000000001640.
大都仅仅是巧合而已. 但精度更高的
   π−8015(625+5389)323308(625+5389)−389" role="presentation"> π?8015(625+5389)323308(625+5389)?389~~~\pi-\frac{80\sqrt{15}(625+53\sqrt{89})^{\frac{3}{2}}}{3308(625+53\sqrt{89})-3\sqrt{89}} ≈0.0000000000000000010023562880081498778451083" role="presentation">≈0.0000000000000000010023562880081498778451083\approx0.0000000000000000010023562880081498778451083
   228663517236794024140821029347477390786609545−π" role="presentation"> 228663517236794024140821029347477390786609545?π~~~\frac{2286635172367940241408\sqrt{2}}{1029347477390786609545}-\pi ≈0.00000000000000000000000568242325601395950" role="presentation">≈0.00000000000000000000000568242325601395950\approx0.00000000000000000000000568242325601395950
   ln⁡262537412640768744163−π" role="presentation"> ln?262537412640768744163?π~~~\frac{\ln262537412640768744}{\sqrt{163}}-\pi ≈0.00000000000000000000000000000022373515038048" role="presentation">≈0.00000000000000000000000000000022373515038048\approx0.00000000000000000000000000000022373515038048
   π−ln⁡(147197952000(236674+3030361)3+744)427" role="presentation"> π?ln?(147197952000(236674+3030361)3+744)427~~~\pi-\frac{\ln(147197952000(236674+30303\sqrt{61})^3+744)}{\sqrt{427}} ≈0.0000000000000000000000000000000000000000000000000000390939627695" role="presentation">≈0.0000000000000000000000000000000000000000000000000000390939627695\approx0.0000000000000000000000000000000000000000000000000000390939627695
   ∑n=1∞n3e2πn19−1−1166" role="presentation"> ∑n=1∞n3e2πn19?1?1166~~~\sum_{n=1}^{\infty}{\frac{n^{3}}{e^{\frac{2\pi n}{19}}-1}}-1166 ≈0.0000000000000000000000000000000000000000000000000000000004848406" role="presentation">≈0.0000000000000000000000000000000000000000000000000000000004848406\approx0.0000000000000000000000000000000000000000000000000000000004848406
∑n=1∞n3e2πn163−1≈2941299.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001153610" role="presentation">∑n=1∞n3e2πn163?1≈2941299.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001153610\begin{align} &\sum_{n=1}^{\infty}{\frac{n^{3}}{e^{\frac{2\pi n}{163}}-1}}\approx2941299.000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000000000000\\&0000000000000000000000000000000000000000000000000001153610& \end{align}
却真的是有深刻数学原理的. 它们有些跟 基本判别式 有关,有些跟 拉马努金级数 有关,有些跟 类数 有关,有些还与 模形式 有关.
|