[时尚穿搭] 连续抛了10000次硬币，每次正反概率1/2，问最多几连正的概率最大？

天天财汇购物网址万年历小说 | 三峰软件小游戏视频

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

首页淘股吧股票涨跌实时统计涨停板选股股票入门股票书籍股票问答分时图选股跌停板选股 K线图选股成交量选股 [平安银行]

股市论谈均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

商业财经科技知识汽车百科工程技术自然科学家居生活设计艺术财经视频游戏--

天天财汇 -> 时尚穿搭 -> 连续抛了10000次硬币，每次正反概率1/2，问最多几连正的概率最大？ -> 正文阅读

[时尚穿搭]连续抛了10000次硬币，每次正反概率1/2，问最多几连正的概率最大？

[收藏本文] 【下载本文】

我玩网络游戏看了很多别人的万场战绩，有人最多连胜18，有人最多只连胜8，大多数人最多连胜都在10-15场左右，于是脑子冒出这个问题，假设一个人玩100…

现有的几个回答用的都是数值模拟，我们来看看怎么从理论的角度解决问题。当然，精确求解确实是很难的--方法上并没有什么难度，用马氏链建个模，把连续若干次正面的情况设成吸收态，然后算这个马氏链在一定时间内被吸收的概率就行了；难的是这样做就需要算一个很大的矩阵的九千多次方，计算量非常大。但是我们可以考虑使用一些近似来简化问题。
我们先想一想，在这一万次掷硬币的结果里面，连续（至少）n个正面的段落的分布有什么规律。首先它明显具有一定的齐次性，也就是说这样的事件发生的概率和时间点没什么关系，从第一次开始连续n个正面和从第九千次开始连续n个正面的概率没什么区别。其次，这样的事件在稍微大一些的尺度上是独立的。离得很近当然不独立，因为这样的段落彼此是不能重叠的；但是只要离远一些，中间有反面分割，彼此之间就独立了。所以尽管不是完全独立，却也是相当接近独立的。最后，既然我们关心的是很多次投掷之后的最大值，那么在每个局部看，出现这么一长串正面就都会是一个小概率事件。
好，总结一下：大量的（近似）独立、齐次（即同概率）的小概率事件。有没有想到什么？
对，是泊松分布！这样的事件发生的次数近似服从泊松分布。学过随机过程的朋友还可以看出来，这些片段的发生近似服从一个泊松点过程。这就为我们解决问题提供了简单易操作的数学工具。
下面都是常规操作了。首先，“最多n连正”的概率直接算起来不太方便，因为这意味着一方面要有n连正，另一方面它还要是最长的。所以更简单的方法是考虑“存在至少n连正”的概率，然后“最多n连正”就等价于“存在至少n连正但是不存在至少n+1连正”。写成数学语言，令M为最大连正的个数，则我们要求的
P(M=n)=P(M≥n)−P(M≥n+1)." role="presentation">P(M=n)=P(M≥n)?P(M≥n+1).P(M=n)=P(M\geq n)-P(M\geq n+1).
而“存在至少n连正”又可以写成“至少n连正的事件发生数大于等于1”，也就是“至少n连正的事件发生数为0”的补集。前面已经说了，10000次抛掷里至少n连正的发生次数近似服从泊松分布，那么现在唯一还不知道的就是这个分布的参数，记为 λn" role="presentation">λn\lambda_n 。注意到这也是泊松分布的期望值，所以想要知道 λn" role="presentation">λn\lambda_n 只需要计算至少n连正的片段的个数的期望即可。
我们用每个片段开始的第一个正面来标记这个片段。对任意一次抛掷，如果它的结果是这样一个片段的开始，那么从它开始的n次抛掷的结果都要是正面，并且前一次的结果是反面。这个组合出现的概率是 2−(n+1)" role="presentation">2?(n+1)2^{-(n+1)} 。所以10000次抛掷得到的这样的点的数量的期望，也就是至少n连正的片段的个数的期望，约为 10000⋅2−(n+1)" role="presentation">10000?2?(n+1)10000\cdot2^{-(n+1)} 。这就是 λn" role="presentation">λn\lambda_n 的近似值。
由泊松分布的概率函数，一个参数为 λn" role="presentation">λn\lambda_n 的泊松分布取0的概率为 e−λn" role="presentation">e?λne^{-\lambda_n} 。因此我们有
P(M≥n)=1−e−λn≈1−e−10000⋅2−(n+1)." role="presentation">P(M≥n)=1?e?λn≈1?e?10000?2?(n+1).P(M\geq n)=1-e^{-\lambda_n}\approx 1-e^{-10000\cdot 2^{-(n+1)}}.
于是有
P(M=n)=P(M≥n)−P(M≥n+1)≈e−10000⋅2−(n+2)−e−10000⋅2−(n+1)." role="presentation">P(M=n)=P(M≥n)?P(M≥n+1)≈e?10000?2?(n+2)?e?10000?2?(n+1).P(M=n)=P(M\geq n)-P(M\geq n+1)\approx e^{-10000\cdot 2^{-(n+2)}}-e^{-10000\cdot 2^{-(n+1)}}.
n是离散的，但是我们还是可以把它当成连续的来处理，通过求导看一下增减性。其导数经整理为
c[e−10000⋅2−(n+2)2−(n+2)−e−10000⋅2−(n+1)2−(n+1)]," role="presentation">c[e?10000?2?(n+2)2?(n+2)?e?10000?2?(n+1)2?(n+1)],c[e^{-10000\cdot 2^{-(n+2)}}2^{-(n+2)}-e^{-10000\cdot 2^{-(n+1)}}2^{-(n+1)}],
其中c是正常数。令此式得0，解 n0" role="presentation">n0n_0 满足
e−10000⋅2−(n0+2)=2e−10000⋅2−(n0+1)，" role="presentation">，e?10000?2?(n0+2)=2e?10000?2?(n0+1)，e^{-10000\cdot 2^{-(n_0+2)}}=2e^{-10000\cdot 2^{-(n_0+1)}}，
因此
n0=−log2⁡(ln⁡(2)/10000)−2≈11.82≈12." role="presentation">n0=?log2?(ln?(2)/10000)?2≈11.82≈12.n_0=-\log_2(\ln(2)/10000)-2\approx 11.82\approx 12.
所以12连正的概率是最大的。当然，为了严格一些，我们应该检查令导数为0得到的 n0" role="presentation">n0n_0 确实对应极大值而不是极小值或者其他驻点，以及11连正确实比12连正的（近似）概率小，此处略过。
最后，我们可以把n取12附近的时候算出来的近似概率和其他回答用数值模拟得到的概率估计，比如
@张宏亮
的结果，做一个比较，看看我们采用的这些近似效果如何：
n近似概率数值模拟90.00750.009100.07950.079110.20800.203120.24810.252130.19380.189140.12150.123150.06810.070
可以看到，用近似方法得到的概率值和数值模拟结果符合得很好。这说明我们采用的近似方法有令人满意的精度。

显然不是两连, 难道你觉得出现一次两连以后再也不出现两连以上的概率很高?
最有可能的最大连续次数为 12 次, 概率为 24.8288%, 精确计算可以用马尔科夫链.
连续次数百分比80.00548%90.74338%107.93316%1120.8104%1224.8288%1319.3875%1412.1472%156.80335%163.60074%171.85233%180.93942%

概率分布大概是这样的
举个例子, 求 20 次投掷, 能达成连续三次的概率
先求能达成三次及以上的概率:
第一下不用管它是正还是反, 总是成立的
第一列表示第二下延续的概率, 有 50%" role="presentation">50%50\% 可能性继续, 也有 50%" role="presentation">50%50\% 可能性归零第二列表示第三下延续的概率, 有 50%" role="presentation">50%50\% 可能性继续, 也有 50%" role="presentation">50%50\% 可能性归零第三列表示已经达成, 不用管之后到底怎么个情况了.
连续(2)=[0.50.500.50000.51]20[100]=[0.01043890.00645160.9831090]" role="presentation">连续连续(2)=[0.50.500.50000.51]20[100]=[0.01043890.00645160.9831090] 连续(2) = \begin{bmatrix} 0.5 & 0.5 & 0\\ 0.5 & 0 & 0 \\ 0 & 0.5 & 1 \\ \end{bmatrix}^{20} \begin{bmatrix} 1\\ 0\\ 0\\ \end{bmatrix} = \begin{bmatrix} 0.0104389\\ 0.0064516\\ 0.9831090\\ \end{bmatrix}
这里的 98.3%" role="presentation">98.3%98.3\% 就是能达成三次以上的概率
然后求能达成四次及以上的概率
连续(3)=[0.50.50.500.500000.500000.51]20[1000]=[0.11579000.06295390.03422740.7870280]" role="presentation">连续连续(3)=[0.50.50.500.500000.500000.51]20[1000]=[0.11579000.06295390.03422740.7870280] 连续(3) =\begin{bmatrix} 0.5 & 0.5 & 0.5 & 0\\ 0.5 & 0 & 0 & 0 \\ 0 & 0.5 & 0 & 0 \\ 0 & 0 & 0.5 & 1\\ \end{bmatrix}^{20} \begin{bmatrix} 1\\ 0\\ 0\\ 0\\ \end{bmatrix} = \begin{bmatrix} 0.1157900\\ 0.0629539\\ 0.0342274\\ 0.7870280\\ \end{bmatrix}
这里的 78.7%" role="presentation">78.7%78.7\% 就是能达成四次及以上的概率
两者作差, 那最大正好三次的概率就是 19.6%" role="presentation">19.6%19.6\%.
然后根据这个原理写代码就行了

probability[n_,k_]:=continuously[n,k]-continuously[n+1,k];
continuously[n_,k_]:=Block[
    {m},
    m=Flatten[{
    {ConstantArray[0.5,n+2]},
    Table[(1-0.5)*UnitVector[n+2,i],{i,1,n+1}]
    },1];
    m[[1,n+2]]=0;
    m[[n+2,n+2]]=1;
    MatrixPower[m,k][[-1,1]]
]
Table[{i,100*probability[i,20000]},{i,8,20}]//ListLinePlot

写完才发现我算的是几连的概率, 不过 0.5 的时候几连和几连正是一样的.

用一些比较流氓的近似，可以快速口算出近似答案12:
定义 m：n = 10000次硬币，最多m连正。
定义“m事件”：从某一刻开始往后出现了 m 连正，但不是m+1连正。
近似：我们姑且认为 “m事件”之间相互独立，且无记忆。
流氓逻辑：既然 m 是最多连正数，m事件发生的期望值应该起码得有一次，但不能超过两次，否则m+1事件发生次数的期望就会超过1。
那么我们就能列出表达式：
n * (1/2)^(m+1) = 1
口算得出：
m = log_2(10000) -1 = 12.288 = 12
手机码字。
值得留意，更严谨的近似由
@Yves S
给出，两个结果是差不多的。

连胜12场的概率最大，高达24.84%
其次是11场，概率是20.82%
其次是13场，概率为19.39%
其次是14场，概率为12.15%
其次是10场，概率为7.93%
其次是15场，概率为6.8%
其次是16场，概率为3.6%
其次是17场，概率为1.85%
其余概率均小于1%
代码

from fractions import Fraction
from functools import cache

N = 10000

@cache
def findProb(n):
    p = Fraction(1, 2) ** (n + 1)
    res = [0] * n
    res.append(Fraction(1, 2) ** n)
    for i in range(n + 1, N + 1):
        temp = res[-1] + (1 - res[i - n]) * p
        res.append(temp)
    return res[-1]

for i in range(10, 18):
    print(i, 0.0 + (findProb(i) - findProb(i + 1)))

输出

10 0.07925023962792647
11 0.2081927146584482
12 0.2483947860937742
13 0.19389940544176268
14 0.1214536236573889
15 0.06800963234402461
16 0.03598979248554171
17 0.018512346991227467

连续12+的概率最大
下面是模拟1万次得到的统计结果

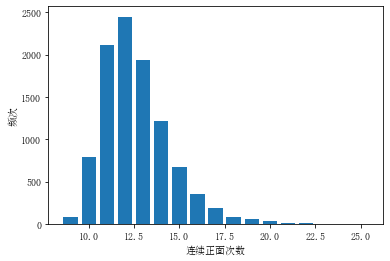
抛N(num_flips)次硬币，统计最大连正的次数。

def flip_coins(num_flips):
    array = [random.randint(0, 1) for _ in range(num_flips)]
    # 初始化
    max_consecutive_ones = 0
    current_count = 0
    for num in array:
        if num == 1:
            current_count += 1
            max_consecutive_ones = max(max_consecutive_ones, current_count)
        else:
            current_count = 0  # 当遇到0时，重置当前连续计数器
    return max_consecutive_ones

模拟一万次

count_list = []
for i in range(10000):  
    num_flips = 10000   #
    max_consecutive_head_count = flip_coins(num_flips)
    count_list.append(max_consecutive_head_count)
freq_table = pd.Series(count_list).value_counts()
freq_df = freq_table.to_frame(name='频次')

真不会用数学算，用程序模拟10000次的平均结果可以参考一下：
抛硬币次数平均最大连胜次数102.311005.9510009.291000012.62
注：第一列是抛硬币的次数，模拟次数是固定的10000次，取平均值。

这是概率中经典的Head runs问题
先说结论：扔n次硬币，连正次数基本上就是 log2⁡n" role="presentation">log2?n\log_2n 这么大。
我们假设有可列次抛硬币实验 Xn,n∈Z" role="presentation">Xn,n∈ZX_n, n\in \mathbb{Z} , P(X=1)=P(X=−1)=1/2" role="presentation">P(X=1)=P(X=?1)=1/2P(X=1)=P(X=-1)=1/2 , 其中1代表正面（head），-1代表反面（tail）。
Ln" role="presentation">LnL_n 代表在时刻 n" role="presentation">nn 时，最大连续正面序列长度（n=10000时的 Ln" role="presentation">LnL_n 就是题主问的随机变量）
那么有以下结论：
Ln/log2⁡n→1   " role="presentation">Ln/log2?n→1   L_n/\log_2n \rightarrow1 \ \ \ a.s. (1)
代入n=10000， log2⁡10000=13.3" role="presentation">log2?10000=13.3\log_2 10000 = 13.3 , 与数值计算出的12偏差不大，造成这种偏差的原因可能是， Ln−log2⁡n=o(log⁡n)" role="presentation">Ln?log2?n=o(log?n)L_n - \log_2 n = o(\log n) 这一偏差项并不是 o(1)" role="presentation">o(1)o(1) 的，具体可以以后算算，我猜偏差项可能服从Gumbel分布之类的。
以下是证明(1)的过程。
设 ln=max{k:Xn−m+1=⋯=Xn=1}" role="presentation">ln=max{k:Xn?m+1=?=Xn=1}l_n = \max\{ k: X_{n-m+1}=\dots=X_n=1\} 为时间为n时从过去到当下的连续的正面数，
Ln=max1≤m≤n lm" role="presentation">Ln=max1≤m≤n lmL_n = \max_{1\leq m\leq n}\ l_m ，即之前提到的在时刻 n" role="presentation">nn 时，最大连续正面长度。
我们分别证明 lim supn→∞Ln/log2⁡n≤1,(2)      lim infn→∞Ln/log2⁡n≥1.(3)" role="presentation">lim?supn→∞Ln/log2?n≤1,(2)      lim?infn→∞Ln/log2?n≥1.(3)\limsup_{n\rightarrow \infty}L_n/\log_2n\leq1,(2)\ \ \ \ \ \ \liminf_{n\rightarrow \infty}L_n/\log_2n\geq1.(3)
以上两者都是在a.s.意义下成立。
我们现证（2）：
首先我们注意到 P(ln=k)=2−k" role="presentation">P(ln=k)=2?kP(l_n= k)=2^{-k} 若 n=k" role="presentation">n=kn=k ， P(ln=k)=2−k−1" role="presentation">P(ln=k)=2?k?1P(l_n=k)=2^{-k-1} 若 n≠k" role="presentation">n≠kn\neq k .
则尾分布有不等式： P(ln≥k)≤2−k+1" role="presentation">P(ln≥k)≤2?k+1P(l_n\geq k )\leq 2^{-k+1} （用不等式可以统一两种情况）
则有 P(ln≥(1+ϵ)log2⁡n)≤0.5⋅n−1−ϵ" role="presentation">P(ln≥(1+?)log2?n)≤0.5?n?1??P(l_n\geq(1+\epsilon)\log_2n)\leq 0.5\cdot n^{-1-\epsilon}
由Borel-Cantelli引理， P(lim supn→∞{ln/log2⁡n≥1+ϵ})=0" role="presentation">P(lim?supn→∞{ln/log2?n≥1+?})=0P(\limsup_{n\rightarrow \infty}\{l_n/\log_2n\geq 1+\epsilon\})=0 0,\ P(\liminf_{n\rightarrow\infty}\{l_n/\log_2n0,\ \exists N,\ \forall n > N,\ \ l_n/\log_2n⇒∀ϵ>0, P(lim infn→∞{ln/log2⁡n<1+ϵ})=1⇒P(∩ϵ↓0lim infn→∞{ln/log2⁡n<1+ϵ})=1⇒P({ω:∀ϵ>0, ∃N, ∀n>N,  ln/log2⁡n<1+ϵ})=1⇒P(lim supn→∞ln/log2⁡n≤1)=1" role="presentation">???>0, P(lim?infn→∞{ln/log2?n<1+?})=1?P(∩?↓0lim?infn→∞{ln/log2?n<1+?})=1?P({ω:??>0, ?N, ?n>N,  ln/log2?n<1+?})=1?P(lim?supn→∞ln/log2?n≤1)=1\Rightarrow \forall \epsilon>0,\ P(\liminf_{n\rightarrow\infty}\{l_n/\log_2n<1+\epsilon\})=1 \\ \Rightarrow P(\cap_{\epsilon\downarrow0}\liminf_{n\rightarrow\infty}\{l_n/\log_2n<1+\epsilon\})=1 \\ \Rightarrow P(\{\omega:\forall \epsilon>0,\ \exists N,\ \forall n > N,\ \ l_n/\log_2n<1+\epsilon\})=1\\ \Rightarrow P(\limsup_{n\rightarrow\infty}l_n/\log_2n\leq1)=1
（这里argument有点复杂，如有朋友知道如何简化以上逻辑，请务必告诉我，谢谢！）
由于 L_n/\log_2n 是 l_n/\log_2n 的子列，所以其上极限也几乎处处不大于1。
下面证明（3），由和（2）中类似的逻辑：
0,\ P(\liminf\{L_n/\log_2n>1-\epsilon\})=1\\ \Leftrightarrow \forall \epsilon>0,\ P(\limsup\{L_n/\log_2n\leq1-\epsilon\})=0">P(\liminf_{n\rightarrow\infty}L_n/\log_2n\geq1)=1\\ \Leftrightarrow \forall\epsilon>0,\ P(\liminf\{L_n/\log_2n>1-\epsilon\})=1\\ \Leftrightarrow \forall \epsilon>0,\ P(\limsup\{L_n/\log_2n\leq1-\epsilon\})=0
由B-C Lemma，我们只需要估计 P(L_n/\log_2n\leq1-\epsilon) 的大小。
由于 P(L_n/\log_2n\leq1-\epsilon)=P(\cap_{k=1}^{n}\{l_k/\log_2k\leq1-\epsilon\}) ，而右边的式子不一定独立所以拆不开，所以我们想到把整个序列拆成几个可以视为独立的块来处理。
我们把长度为n的序列拆成每段长为 \left[ (1-\epsilon)\log_2n \right]+1 的若干个区间，在每个区间上设置一个随机变量 T_k,\ \ k=1,2,\dots, K ，如果区间上全都是1，则T=1 ，其它情况时 T=0 。
我们有 P(T=1)\geq 0.5\cdot n^{-(1-\epsilon)} (没除干净的尾段也符合)
由于 L_n\leq(1-\epsilon)\log_2n 时 T_k 上一定都不全是1，并且 T_k 之间独立，我们有：
P(L_n/\log_2n\leq1-\epsilon)\leq P(T=0)^K
取充分大的n，使得 K=\lceil n /(\left[ (1-\epsilon)\log_2n \right]+1)\rceil\leq n/\log_2n
此时 P(T=0)^K\leq(1-\frac{1}{2\cdot n^{1-\epsilon}})^{\frac{n}{\log_2n}}\leq\exp(-\frac{n^\epsilon}{2\log_2n})
右式的求和收敛，故命题得证。
我们注意到上述证明没有用任何和2相关特别的性质，所以其实也可以用这个几连胜的数字来估计这个玩家的胜率： \log_{1/p}n = L_n\Rightarrow p =n^{-1/L_n} ，例如如果一个人一万场最大连胜是18，那么可以估计他的胜率为 (\sqrt[18]{10000})^{-1}\approx60\% 。
参考资料：Durrett PTE 5th edition.

严格的来说是是0次连正的概率最大。高达50%
下面是稍微另类的用php而且用数组来统计的代码段。(这段代码跟题意有点不符，)

<?php
	//模拟一万次丢硬币，组成1万长度的字符串
	$str='';
	for ($i = 1; $i <= 10000; $i++) {    
		$str=$str.mt_rand(0, 1);
	}

	$stat_arr=explode('0',$str);//由0截取字符串形成数组
	$rs=array_count_values($stat_arr) ;//统计值出现的次数
	//打印结果
	echo "<pre>";
	print_r($rs);
	echo "<pre>";	

?>

下面是结果。

Array
(
    [11] => 623
    [1] => 1270
    [] => 2397
    [11111] => 71
    [111] => 316
    [111111] => 46
    [1111] => 163
    [1111111] => 15
    [1111111111111] => 1
    [111111111] => 5
    [1111111111] => 3
    [11111111] => 14
    [11111111111] => 1
    [111111111111] => 1
)

所以，上面代码哪个地方错了呢？
上面连续出现正的机会是递减的。出现一次的最多，二次依次减少。
因此这道题是语文题，而不是数学题。
核心就是理解：最多几连正这五个字
理解了上面最多几连正这几个字后，
即模拟1万次上面的数据，分别求出最多连正的次数即可。
m = log_2(10000) -1 = 12.288 = 12
其值如上。

每次衰减一半的概率，又要连，那不是连两次最高么？
为啥答案前排都是十几次
突然觉得白上学了！
卧槽，看了评论我悟了，求的不是连续正几次的概率最高，求的是一万次的事件中，出现连胜的情况中，最多出现的连胜次数是几次。
换句话说，如果连续出现正三次，是不被当做连续正两次的事件的。
没想到，概率从上学时候一直到现在，最大的问题一直是如何理解题目里没表达具体出来的内容。

12。
重新陈述一下题目，感觉很多答主理解错了
对于扔n次硬币的结果，如n=13：
正正反反正正正正反正反反正
连续出现“正”的最大长度为4
我们称这次试验结果的正游程为4。
当n=10000时，考虑全部试验结果，共2^10000个，对k=1，2...，10000，正游程为k的试验结果有m（k）个，对于不同的k，求使得m（k）最大的k

[收藏本文] 【下载本文】

时尚穿搭最新文章

加:2024-04-01 22:32:10 更:2024-04-01 22:35:10

股票涨跌实时统计涨停板选股分时图选股跌停板选股 K线图选股成交量选股均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

网站联系: qq:121756557 email:121756557@qq.com 天天财汇