| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 2024 年阿贝尔奖授予解释随机性的数学家 Michel Talagrand,这项研究有哪些意义? -> 正文阅读 |
|
|
[时尚穿搭]2024 年阿贝尔奖授予解释随机性的数学家 Michel Talagrand,这项研究有哪些意义? |
| [收藏本文] 【下载本文】 |
|
[图片] 现代世界是由不断流动的 随机事件组成的,从商业物流到凝聚态物理学,一切事物都受随机性的影响。随机性能够以多种方式出现,一种最常见的,也可以说… |
|
Michel Talagrand对平均场自旋玻璃模型得到的数学结果算是在数学物理中影响深远。 自旋玻璃模型在物理上应用是很广泛的,其实对它的研究早已超出物理学,还有关生物学(神经网络,种群遗传),金融学(市场微观结构),计算机科学(组合优化,Bool可满足性,随机分配,纠错码)。 这里就不展开细节了,计算机科学方面现在已经有非常多的教材了,感兴趣的读者可以自己去研究,教材例如中文的,周海军著的《自旋玻璃与消息传递》,英文的,Marc Mézard和Andrea Montanari著的Information, Physics, and Computation,Hidetoshi Nishimori著的Statistical Physics of Spin Glasses and Information Processing: An Introduction。 自旋玻璃模型最早是为了解释磁性合金特殊的热力学行为提出来的,例如铁,锰,铬弱稀释在金,银,铜中,这种合金系统是动力学远离平衡的,表现出老化和年轻化等非常特别的行为。玻璃也具有这种行为,而磁性来自自旋,所以这种磁性合金称为自旋玻璃。 自旋玻璃模型的设定并不复杂,就是两自旋间有随机耦合强度的相互作用。但就是这样一个数学上看起来非常简单的模型,一直做不到严格理解。Talagrand获得严格结果的也不是原本的模型,而是它的平均场版本,其实已经作过一步近似了。 2021年获得Nobel奖的理论物理学家Giorgio Parisi,根据他的物理直觉对平均场自旋玻璃模型的解作了假设,然后还取了数学家看来没有道理的极限,算出了这个模型的无穷体积压强。这种假设和取极限,数学家是无法接受的,但物理学家会觉得足够有说服力了。三十年中都没有获得严格的数学证明。 直到2003年,数学家Francesco Guerra[1]证明了,这个模型的无穷体积压强的上界就是Parisi的计算结果;而在2006年,今年获得Abel奖的数学家Michel Talagrand[2]证明了,这个模型的无穷体积压强的下界就是Parisi的计算结果。那么加起来就说明,Parisi的计算结果是精确的。 但是,不作平均场近似的自旋玻璃模型,它的严格数学理论还是开放问题,需要数学家继续努力。 参考^F. Guerra, Broken replica symmetry bounds in the mean field spin glass model, Communications in Mathematical Physics, 233: 1–12 (2003).^M. Talagrand, The Parisi formula, Annals of Mathematics 163: 221–264 (2006). |
|
Michel Talagrand 是概率学的一位传奇人物。阿贝尔奖是授予一个数学家以表彰他的全面的贡献的奖项,而不是像诺贝尔奖一样主要针对一项工作,所以说“这项研究有什么意义”稍微有点偏。更准确的问法是“Talagrand的(各项)工作都有什么意义”。 阿贝尔奖的颁奖词主要提到了Talagrand在三个方面的工作:随机过程的极大值、测度的集中和自旋玻璃,我并不都很熟,只能说抛砖引玉,谈一谈自己的理解。 1. 随机过程的极大值。这个方向我还算比较了解。它是极限值理论(extreme value theory)的一部分。极限值理论可以看作是中心极限定理的反面—中心极限定理关心均值会怎么样,而极限值理论关心远离均值的极限值会怎么样。它的最简单的版本就是研究一列独立同分布的随机变量的最大值(在合适的归一化之后)满足什么分布,这就是经典的极值定理(extreme value theorem)。但是无论是从理论还是应用的方面,独立同分布的条件都太强了。特别是我们一般见到的随机过程在不同时间都不会是独立的,而是会有相互影响。这样,就需要开发关于随机过程的极大值的理论,好刻画它的分布。Talagrand在这方面做了大量的工作。如颁奖词所说,这些工作有非常明显的应用价值,如预测洪峰水位、抵抗金融风险等。 |

|
|
来源:https://www.cityam.com/uk-weather-storm-desmond-threatens-to-bring-floods-heavy-rain-and-strong-winds-as-the-met-office-issues-amber-alert/ 2. 测度的集中。先想一个问题:夹在赤道与北纬30度之间的地域,和北纬60度以北(即夹在北纬60度和北纬90度之间)的地域一样大吗? 答案是不一样。因为赤道附近的纬线圈比接近极地的大很多,所以同样的宽度,面积会大很多。换句话说,如果我们在地球表面均匀随机地取一个点,那么它大概率会比较接近赤道。 这个现象在一维的圆环上不存在,在地球(二维球面)上存在但还不是很明显,随着维数的上升变得越来越显著。在高维球面上,几乎所有的“测度”都集中在赤道周围一条很窄的带子里。换成概率的说法就是随机取一个点,它大概率会在这么个带子里。这就是“测度的集中”。Talagrand 的工作刻画了这种测度集中的现象。很多人都听说过著名的“Talagrand不等式”,就是关于一种特定的测度的集中的。测度的集中在高维统计、机器学习中有广泛的应用。 |

|
|
3. 自旋玻璃。自旋玻璃在物理上是一种磁性状态,其中每个点的磁矩是随机的。它并不是玻璃 ,之所以叫玻璃,是因为这种随机行为和玻璃中结晶的无序性有一些相似。抽象成概率模型,一般就是在一些格点上随机有不同方向的自旋,这些自旋会决定系统的能量(哈密顿量),能量又会在一定温度下转换为这个状态出现的概率。概率学家就可以研究不同状态出现的概率。我的研究方向和自旋玻璃离得比较远,Talagrand在这方面的贡献还是留给更专业的朋友来解读吧。 |
|
|
来源:https://en.m.wikipedia.org/wiki/File:Spin_glass_by_Zureks.svg 另:老爷爷其实也有比较清秀的照片 |

|
|
来源:https://en.m.wikipedia.org/wiki/Michel_Talagrand |

|
|
来源:https://twitter.com/Sorbonne_Univ_/status/1135895982611337222/photo/1 |
|
一切事物都受随机性的影响。作为当今世界上对随机过程理解最深刻的人,法国概率理论家米歇尔·塔拉格兰做出了深远的贡献,他的工作重塑了概率论的几个领域。他是一位杰出的数学家,也是一位出色的问题解决者。 撰文 | 嘉伟 我们的人生,会经历无数的随机事件。它们有些是预料之中的,有些则完全出乎意料。就算是当今世界上对随机过程理解最深刻的人,也无法预知自己会在北半球春分这一天,摘得数学界的最高奖项之一。 北京时间2024年3月20日,法国概率理论家米歇尔·塔拉格兰(Michel Talagrand)被授予了阿贝尔奖,以表彰他对随机过程深刻而复杂的理解。这是数学家事实上的终身成就奖。奖金高达750万挪威克朗(约合70万美元),这是为了弥补诺贝尔奖项里未设立数学奖,以及菲尔兹奖奖金微薄的缺憾。 当得知自己是今年的阿贝尔奖得主时,“我的脑子一片空白,”塔拉格兰说,“我刚学习数学的时候,(它)一点也不时髦。(随机过程)被认为是低劣的数学。我获得这个奖项的事实绝对证明了事实并非如此。” 人类在不确定性中寻找确定性。随机过程是一门以追求确定性为目标研究不确定性和随机性的学科。它不仅仅是关于概率的计算,更是关于理解复杂系统中的模式和规律。塔拉格兰通过对随机性的深入研究,将高维几何工具应用于复杂的概率问题,向我们揭示出隐藏在表象之下的结构和美。即使在最不可预测的环境中,也存在着一种内在的逻辑和秩序。 塔拉格兰相信,正是生命中那些不可预测的随机事件,赋予了他某些品质,推着他走上了数学之路。 童年:命运投下的阴翳 塔拉格兰出生时便确诊患有先天视网膜缺陷。在他5岁时,一只眼睛因视网膜脱落而彻底失明。 他在法国里昂勉强读完了小学,虽然他对科学很感兴趣,但他不喜欢学习,因为读书、写字会带来用眼负担。塔拉格兰从小就被笼罩在某天再也无法看到光明的恐惧阴影之中。 仿佛是为了佐证著名的墨菲定律——担心的坏事总会发生,在他15岁的时候,另一只眼睛连续三次视网膜脱离,迫使他在医院住了一个月,眼睛缠着绷带。 |

|
|
法国概率理论家米歇尔·塔拉格兰15岁时与妹妹的合照。此时塔拉格兰另一只眼睛的视网膜亦出现问题,需经常前往医院观察和治疗。丨图源:香港《明报》 幸运的是,塔拉格兰有一位全心支持他的父亲。后者也是一位数学教授,对塔拉格兰的数学人生有着深远影响。 父亲对他充满信心,即使他在考试中的拼写和语法出现错误,父亲仍然尽力争取他升上高中的机会。在他15岁进行眼部手术和术后修养期间,父亲每天都从学校赶来看望,并教授他一些数学理论,借此让他的大脑忙碌起来,逐渐培养了他对这门学科的兴趣。 出院后,他一学期已缺课4个月之久,但他坚持自学完成了数学和物理课程。塔拉格兰所就读中学的校长要求他重修上一学期的课程,但他的父亲相信他已经掌握了课程内容,说服校长让他参加年级考试,最终证明了他的能力,直接成为了数学和物理科的优秀学生。 几何是塔拉格兰的苦手,每当遇到困难时,他都会向父亲请教,而父亲总是耐心解答,成为他坚持不懈的动力。渐渐地,他开始自己解决大部分数学问题,这成为了他学习阶段的极大乐趣,甚至成为了抚平眼疾痛苦的一种安慰。“这就是我掌握抽象力量的方式。”塔拉格兰在2019年获得邵逸夫奖后写道。这是另一个重要的数学奖项,奖金为120万美元。 米歇尔·塔拉格兰教授直言,如果没有眼疾,他或许会选择不同的人生道路。一只眼睛失明,另一只眼则在10多岁屡次视网膜脱落。对他来说,时间尤其宝贵,因担心自己某天一觉醒来完全失明,所以要在能看得见的时候,把所有精力集中于学习之上。他回忆说,当时自己的视力还不算太差,很近的东西都能看得清楚,“只要出现视网膜脱落的症状,就尽快求诊,情况是可以控制的,只是眼疾令我经常活在害怕失明的惶恐之中。” 他最大感受是,他在学习过程中付出了最大的努力,而收获也超出了他的预期,这是最珍贵的成就。 转机:命运女神的青睐 专注于学业后,塔拉格兰在数学方面的表现尤为出色。1974年大学毕业后,他被欧洲最大的研究机构法国国家科学研究中心(CNRS)聘用,在那里他一直工作到2017年退休。 一开始,濒临失明的阴云仍悬在塔拉格兰的头顶。他后来回忆说:“我知道眼球转动时,眼内玻璃体会因黏着视网膜而容易导致视网膜脱落,于是我研究了一套提前自我诊断前兆的方法,让我减轻了对视网膜脱落的恐惧。” 在1981年,不可预测的小概率事件发生了——医疗技术的发展带来激光手术,恰好可以治疗他的视网膜问题,让他摆脱了随时可能失明的痛苦。 在此期间,他获得了博士学位,赢取了一位统计学家的芳心。他对自己未来的妻子一见钟情——认识仅三天后便向她求婚。在各种意义上,Wansoo Rhee女士成了塔拉格兰的幸运女神,除了带来美满的婚姻外,还使他转向了概率论——他学术生涯中最成功的领域。他发表了数百篇关于概率论的论文。 2019年,在台上当众发表邵逸夫奖获奖感言时,塔拉格兰饱含深情地回忆道: “我一生中最幸运的事件是在俄亥俄州肯特市遇到了一位了不起的博士生,她立即俘获了我的心。认识3天后,我便向她求婚。你疯了,她说。我跟着她去了韩国。她又把伤心的我送回了法国。 “在回家的路上,我们在香港停留了一下。我恰巧知道一个信誉良好的首饰商人的地址,在那里我给她买了一条我能买得起的最好的珍珠项链作为临别礼物。我的真挚举动打动了她,两人的故事得以继续。 “她的父亲是韩国知名学者,从小就相信学术成就是人生的最高价值。我常常在想,她决定嫁给我的原因,是因为我的数学水平,而非我帅气的外表(笑)。 “尽管她拥有充实的职业生涯,但她一直非常支持我。我从来没有听见过我最害怕的那句话:现在不是工作的时候。 “这并不意味着我忽视了家人。数学成功的秘诀是每天工作到筋疲力尽,但不能更多。当她说我一生中99%的时间都花在数学上,1%的时间花在她身上时,不要相信她!她至少得到了2%。 “有了完美的配偶,剩下的一切都很容易。我希望我能说我对数学有一个宏伟的愿景,但现实却大不相同。我只懂很少的数学。我只是试着解决我遇到的问题,总是试图追根究底。我没有研究时髦的领域,但我专注于简单的通用结构,因为那里有重要的问题。我非常感谢Gilles Pisier,Vitali Milman和其他人,他们向我介绍了我最成功的领域。现代科学就像一座宏伟的庙宇,在永恒的建造中。我很自豪我能为它的地基贡献一块小砖。” 成就:教我们“看”随机的大师 其他数学家也会同意,塔拉格兰的工作“改变了人类看待世界的方式”。阿贝尔奖委员会主席赫尔格·霍尔登(Helge Holden)认为,“通过随机过程描述和模拟现实世界的事件正变得非常流行。塔拉格兰的工具箱马上就出现。” 想一想不久前火爆一时的AI视频生成工具sora,大多数人都会赞同上面的看法。 塔拉格兰的职业生涯始于研究高维几何空间。“10年里,我没有发现自己擅长什么。”他说,但他并不后悔这段弯路。这最终将他引向了概率论,在那里“我的经历带来了另一种观点……给我一种以不同方式看待事物的方式。“这使他能够通过高维几何学的视角来检查随机过程。 “他用他的几何直觉来解决纯粹的概率问题。” 普林斯顿大学数学教授阿萨夫·诺尔(Assaf Naor)说。 随机过程是事件的集合,其结果以可以建模的方式根据机会而变化——比如一系列抛硬币、气体中原子的轨迹或每日总降雨量。数学家想要了解个体结果和总体行为之间的关系。 塔拉格兰花了15年时间开发出一种称为generic chaining的技术,使他能够创建与这种随机过程相关的高维几何空间。诺尔评价称,他的方法“给了你一种从几何中看最大值的方法。” 该技术非常通用,因此应用广泛。如果我们想要分析依赖于数千个参数的海量高维数据集。为了得出有意义的结论,需要保留数据集最重要的特征,同时仅用几个参数来表征它。如分析和比较不同蛋白质的复杂结构的工作就是如此。许多最先进的方法通过应用随机操作,将高维数据映射到低维空间来实现这种简化。数学家可以使用generic chaining确定此过程引入的最大误差,从而使他们能够确定简化数据集中未保留某些重要特征的可能性。 塔拉格兰的工作不局限于分析随机过程的最佳和最坏结果。他还研究了在平均情况下会发生什么。 在许多过程中,随机的单个事件总体上会导致高度确定性的结果。如果测量是独立的,那么总数就变得非常可预测,即使每个单独的事件都无法预测。 为了介绍度量集中(Concentration of measure)的概念,这里先提供一个非常有意思的思考题,大家可以测试一下自己的概率直觉。 假设稍后要掷硬币100 次——可以给出一系列正面(H)和反面(T)的序列。 现在你有选择权,可以选择积分规则。 规则A:对于序列中的每个HH,你会都会得到一分;对于每个HT,对手都会得一分。 规则B:反过来,对于序列中的每个HH,对手会都会得到一分;对于每个HT,则你得一分。 比如说序列片段HHHT,按A规则就是你得2分,对手1分。 问:为了积分高于对手,你应该选择哪条规则?又或者说,两条规则的获胜概率是一样的? |
|
|
抛一枚均匀的硬币。你无法提前说出将会发生什么。翻转10次,大约66%的概率会出现4、5或6个正面,接近5个正面的期望。但抛硬币1000次,99.7%的情况下,正面朝上的概率会在450到550之间,结果更加集中在期望值500附近。在平均值附近,结果异常尖锐。 “尽管某些事物具有如此多的随机性,但随机性会自行抵消,”诺尔说,“最初看似一团糟的事情实际上是有组织的。 这种现象就是度量集中性,也发生在更复杂的随机过程中。塔拉格兰提出了一系列不等式,使得对集中性的量化分析成为可能,并证明它可用在许多不同的情况。他打造的工具标志着该领域的新阶段。他在2019年的论文中写道,第一次证明这种不等式存在是“一次神奇的经历”。他“一直处于兴高采烈的状态”。 塔拉格兰特别自豪的是,他随后得出了约束集中性的不等式。“要得到一个适用于全宇宙的结果并不容易,何况同时又有一个易于解释的一页证明。”他说。 他高兴地回忆,他曾被一家出租车服务公司的车主认出了名字,因为后者在商学院的概率课上学到了以他命名的不等式。“这太了不起了。”他说。 |

|
|
当代数学大师,2024年阿贝尔奖得主米歇尔·塔拉格兰发表获奖感言| 图源: The Abel Prize官网直播画面 就像他的generic chaining一样,塔拉格兰的集中不等式出现在各个数学分支中。“它的应用范围之广真是神奇。”诺尔说,“塔拉格兰的不等式是将事物联系在一起的螺丝钉。” 类似的方法已被用于证明组合学、物理学、计算机科学、统计学和其他环境中的集中现象。 最近,塔拉格兰运用他对随机过程的理解来证明一个关于自旋玻璃的重要猜想。自旋玻璃是一种磁性合金材料的亚稳定状态。在这种状态中,材料的磁矩方向(自旋)是随机冻结的,显示出长程无序性。这与铁磁性状态和反铁磁性状态不同,后两者的磁矩分布是长程有序的。自旋玻璃的“玻璃”一词实际上是指这种长程无序状态,类似于我们通常所说的玻璃——玻璃是非晶体。 令塔拉格兰感到沮丧的是,尽管自旋玻璃在数学上定义明确,但物理学家比数学家更了解它们。“这是我的眼中钉。”他说。他证明了一个结果——关于所谓的自旋玻璃的自由能——为一个更数学的理论奠定了基础。 在他的整个职业生涯中,塔拉格兰的研究一直以“这种退后一步并找到在任何地方都可以重复使用的一般原则的能力”为标志,诺尔说。“他重新审视,从各种角度思考一些事情。最终,他提出了一个见解,成为每个人都在使用的方法论。” “我喜欢慢慢消化理解简单的事物,因为我脑子很慢。”塔拉格兰说,“所以我总是考虑了很长一段时间。”他的驱动力是“以一种纯粹的方式深入理解一些东西,这使得理论变得容易得多。然后,下一代人就可以从那里开始,按照自己的方式取得进步。 在过去的十年里,他通过编写教科书来实现这一目标——不仅仅是关于随机过程和自旋玻璃,还有关于他根本不擅长的领域——量子场论。他本来想了解一下这一领域,但意识到他能找到的所有教科书都是由物理学家写的,也是为物理学家写的,而不是为数学家写的!所以他自己写了一本。“在你不能发明新东西之后,你还可以解释它们。”他说。 现在,塔拉格兰正在用他最近几年获得的各项奖金(如邵逸夫奖的120万美元)的一部分,以及刚刚的阿贝尔奖奖金,来设立自己的奖项,以“表彰年轻的研究人员在我毕生致力于斯的领域里所能取得的成就“。项目名为Become RICH with my prizes(用我的奖金变富有吧~,链接见参考[6])。 他对自己的学生和读者向来十分慷慨:“如果你急于得到我的书,但又负担不起购买费用,可以尝试在搜索引擎中输入‘library genesis’。我不鼓励盗版,但这个网站让我少跑了很多趟图书馆,可惜图书馆没有电子版的旧书。” 最后,关于之前的那个思考题,答案是选B。您猜对了吗? 如果只投掷硬币5、6次,可以发现规则A更加有利。但是当次数足够多的时候,HT获胜的概率变高了。因为H和T的数学期望是一样的,但是分布不同。相当于说HH最高时可能得90分,但此时H分布过于集中,就意味着在其余片段里H变得稀少。HT最高50分,但更平均。A策略超过50分的部分都浪费了。 此即前文所言,由于集中现象,“随机的单个事件总体上会导致高度确定性的结果”,“尽管某些事物具有如此多的随机性,但随机性会自行抵消”。虽然H和T本身都是随机的,但因为我们所关心的,准备测量的分布(HH和HT)的集中程度有所不同,数据足够大的时候,就出现了整体上相对不随机的结果。 从这个例子中,大家应该也能领会概率和随机现象是如何地反直觉。 参考资料 [1] La page de Michel Talagrand:https://michel.talagrand.net/[2] Microsoft Word - speechfinal.docx (http://talagrand.net)[3] Normal distribution - Wikipedia[4] Concentration of measure - Wikipedia[5] Michel Talagrand Wins Abel Prize for Work Wrangling Randomness | Quanta Magazine[6] https://michel.talagrand.net/prizes/ 本文受科普中国·星空计划项目扶持 出品:中国科协科普部 监制:中国科学技术出版社有限公司、北京中科星河文化传媒有限公司 |

|
|
|
|
先来介绍一下基本情况,有时间继续更新技术细节。 米歇尔·塔拉格兰德(Michel Talagrand)于1952年2月15日出生于法国,主要研究泛函分析和概率论及其应用。他是法国国家科学研究中心(CNRS)的数学博士,自1985年以来一直担任法国国家科学研究中心(CNRS)的研究员,并且是巴黎数学研究所泛函分析小组的成员[1]。 Michel Talagrand于今年(2024年)获得Abel奖,Abel奖官网给出的获奖原因是[2]: for his groundbreaking contributions to probability theory and functional analysis, with outstanding applications in mathematical physics and statistics 译文:表彰他在概率论和函数分析方面的开创性贡献,(这)在数学物理和统计学方面有着杰出的应用 他的获奖工作主要来自三个领域:随机过程的上确界、测量的集中性、自旋玻璃态。 Abel奖官网给出的介绍文章中[3],对这三个领域有一些科普性的解释,大略总结一下,就是如下几点: Talagrand估计了特定不确定性的严格而紧的上确界Talagrand考察了高维空间中数据分布的集中性。由于Gauss分布的普遍性,Talagrand的工作对于凝聚态物理中的“自旋玻璃态”(spin glass)的有可能的应用。 Michel Talagrand在概率论和相关领域的工作使用新颖的技术产生了一些关键的见解和证明。这些结果本身在数学上是美丽的,而物理系统会使这些结果更有意义。 介绍一下自旋玻璃态,其他两种待会写。 所谓“自旋玻璃态”(spin glass)是指一种以随机性为特征的磁态。如下图所示,第一个图是自旋玻璃态的随机自旋结构,第二个图是铁磁态的有序自旋结构。 |

|
|
目前对于自旋玻璃态的一个重要模型是Sherrington–Kirkpatrick模型,它是一种Ising模型,对应的是自旋玻璃态的平均场近似,具有如下形式的Hamiltonian: H=−∑i<jJijSiSj" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">H=?∑i<jJijSiSjS_i 是晶格点处的半自旋粒子的Pauli矩阵; Jij" role="presentation">JijJ_{ij} 是自旋-自旋相互作用的磁性项,称为键或链接变量。 Michel Talagrand在此上的工作与Sherrington–Kirkpatrick模型的Parisi公式有关,这组公式描述的是自旋玻璃态的自由能[4] limN→∞1NElog⁡∫exp⁡(HN(σ))dPN(σ)" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">limN→∞1NElog?∫exp?(HN(σ))dPN(σ)\displaystyle\lim_{N\rightarrow\infty}\frac{1}{N}\mathbb E\log\int\exp(H_N(\sigma)){\rm d}P_N(\sigma)\\ Talagrand的工作是证明了Parisi公式的完备下界[5],这对于Sherrington–Kirkpatrick模型的研究具有基础性意义。 参考^参见wiki https://en.wikipedia.org/wiki/Michel_Talagrand^https://abelprize.no/abel-prize-laureates/2024^https://abelprize.no/sites/default/files/2024-03/glimpse_of_the_laureates_work_AbelPrize_2024.pdf^https://perso.ens-lyon.fr/jean-christophe.mourrat/parisi.pdf^https://abelprize.no/sites/default/files/2024-03/Talagrand%20and%20his%20mathematics.pdf |
|
在learning theory里经常见到这个数学家的名字 |

|
|
|

|
|
|
|
Talagrand能拿奖主要还是他对concentration inequality和高斯过程的理论贡献。这些理论或者应该说方法论,例如chaining, Majorizing,现在已经内化成为概率统计甚至是机器学习理论研究的基础方法论了,影响了后来一大批概率和统计学家。 国内做概率研究特别是高斯过程的人少一点(好像我见到的本科生研究生基本都会认为高斯过程是机器学习那种高斯过程╮(╯_╰)╭),或许都会认为他能拿奖是因spin glass。但是spin glass只能算是他的理论在数学物理中的应用。 |
|
祝贺米歇尔·塔拉格兰德。 米歇尔·塔拉格兰德因其在概率论、泛函分析以及这两个领域在数学物理和统计学中卓越的应用成果而荣获了数学界的重要荣誉——阿贝尔奖。 该奖以挪威数学家尼尔斯·亨里克·阿贝尔的名字命名,由挪威科学与文学学院每年颁发,奖金750万挪威克朗(约合70万美元)。 塔拉格兰德的工作不仅加深了我们对概率论的理解,而且还在面对不确定性时设定了新的理论边界。他的研究涵盖了高斯过程,这是一种能够描述众多(甚至无限多)相互关联的随机变量的方法。 高斯过程在实际应用中,比如环境污染物浓度随时间变化的测量等方面起到关键作用,塔拉格兰德通过对高斯过程的研究,特别是在泛型链理论上取得突破,为理解和预测随机系统的极端值提供了精确的界限。 另外,塔拉格兰德在概率测度的集中问题上也做出了重要贡献。他运用大数定律,展示了在重复实验中,随机事件的概率趋于稳定,这一原理在赌博场景下可以用来预测长期收益,而在更为复杂的随机系统中,他的研究成果揭示了尽管单个事件难以预测,但大量事件的交互往往会形成相对确定的结果。 塔拉格兰德还涉足统计物理学领域,为自旋玻璃系统的行为提供了数学支持。自旋玻璃是一种内部结构混乱的磁性材料,其中自旋(原子的磁矩)由于局部相互作用而呈现出复杂随机排列。2021年诺贝尔物理学奖得主之一的Giorgio Parisi提出了一种描述自旋玻璃自由能的公式,而塔拉格兰德通过其开创性的文章,为这一公式提供了严格的上下界证明。 追溯历史,概率论的起源可以追溯到16和17世纪,其最初的灵感源自赌博现象。 |

|
|
如掷骰子游戏中,理解各个数字出现的概率均等至关重要;而在考虑投掷两个骰子并赌注于总和时,认识到押注7比押注2更具优势,因为共有6种组合加和为7,而只有1种组合加和为2。 |
|
|
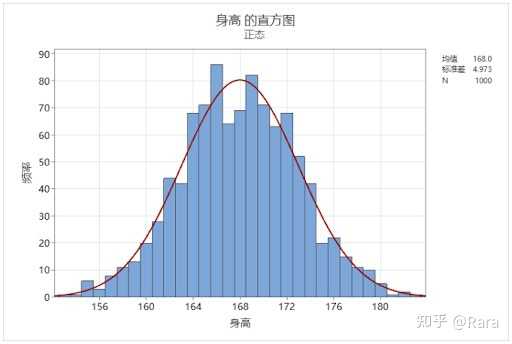
尽管概率论起始于对赌博行为的量化,但它后来演化成为理解和预测各类随机现象规律的强大工具。 比如,在探讨英国人群体身高的分布时,由于无法测量每个人的身高,可以选择随机抽样100人进行测量,所得数据绘制的直方图将展现出接近正态分布或高斯分布的特征,其中峰值代表了最常见的身高,也就是平均身高,而分布曲线的两边逐渐变缓,反映着极端身高出现的可能性递减,曲线宽度则体现了身高的变异性。大量自然和社会现象,如鞋码大小、血压读数等,都符合类似的高斯分布规律,甚至掷骰子次数足够多后的总和分布也会趋向于高斯分布,尽管各例中的具体均值和标准差不同,但背后的数学形态却保持一致。 在概率论的探究中,塔拉格兰德的研究显著推进了我们对不确定性和随机过程极限的认知。 他关于高斯过程的工作最为突出,这类过程描述了一个包含许多(甚至无穷多)相互关联且各自遵循正态分布的随机变量集合。 例如,在连续监测空气中污染物浓度时,每个观测值都可能服从正态分布,并且相邻时刻的测量值可能存在相关性。利用高斯过程的概念,科学家能够估算在某一时间段内浓度的期望平均值。 塔拉格兰德在研究极端值的问题上也取得了重大突破,他基于Xavier Fernique和Richard Dudley的研究成果,发展了泛型链理论,为预估高斯过程中的最大或最小值提供了严谨的界限。这一成果对于决策制定至关重要,如在预测空气污染严重程度的情况下,若预计极端值异常大,便可能要求采取紧急应对措施。 此外,塔拉格兰德在概率测度的集中性质方面也有独特贡献。从掷骰子这一直观例子出发,当进行大量重复投掷时,依据大数定律,某个数值出现的频次将趋近于其理论概率,这对于赌场经营者而言意味着即便无法预测单次游戏的结果,仍能通过概率统计预测长期盈利状况。而塔拉格兰德成功地将这种概率集中的思想推广到更一般的情形,证明了在更广泛的随机事件互动中,尽管单个事件显得随机,整体上却能展现出可预见的规律性,并对不确定性提供了量化的控制范围。 塔拉格兰德的研究并未止步于经典概率论,他还触及到了统计物理学和自旋玻璃等复杂领域。 自旋玻璃作为一种含有随机排列磁性自旋的无序材料,其内在结构与行为引发了诸多挑战。 |

|
|
意大利物理学家Giorgio Parisi因在无序和随机系统研究方面的成就,于2021年荣获诺贝尔物理学奖,其中就包括提出自旋玻璃系统的自由能公式。然而,Parisi并没有提供完整的证明。塔拉格兰德在这项工作中发挥了关键作用,他在一篇开创性的文章中成功确立了该公式下限的证明,这一成就不仅增进了对自旋玻璃特性的理解,还为其它无序系统的数学建模提供了思路。这类数学模型还与驱动当前人工智能进展的深度学习算法建立了联系。 生于1952年的塔拉格兰德一直在法国巴黎国家科学研究中心(CNRS)工作,他热衷于探究自己喜欢的问题。 Able 奖网站上引用了他的一句话:“这几乎是瞬间的。现在你看到了,而之前你还没有看到。经过这样的进展,你可能对问题有了更清晰的认识。” 在他的个人网站上,塔拉格兰德标出“数学赋予你翅膀”,并设立了一个名为“用我的奖品致富”的栏目,资助那些备受关注的数学问题的研究。 在他的论文《对独立性的新看法》中,他认为“数学往往取决于找到正确的观点:一旦找到了正确的观点,困难的想法就会突然变得简单,或者像数学家所说的那样“微不足道””。 |
|
2024年,阿贝尔奖授予了法国数学家Michel Talagrand,以表彰他在概率论和随机过程领域的杰出贡献。这一领域的研究对我们理解现代世界中无处不在的随机事件具有重要意义。 随机过程是一系列随机事件的集合,这些事件随着时间的推移而发展。例如,股市的波动、天气的变化、以及粒子的运动都是随机过程的例子。在数学和物理学中,随机过程是非常重要的研究对象,因为它们帮助我们从理论上描述和理解自然界和社会现象中的不确定性。 Talagrand的研究主要集中在三个领域。一是随机过程的上确界。这是随机过程中预期最大值的数学概念。想象一下,如果你想知道明年冲击海滩的最大海浪可能有多高,这就需要了解随机过程的上确界。Talagrand通过发展通用链式(generic chaining)理论,为高斯过程的上确界提供了清晰的上界和下界。这个理论在工程学、金融学和保险领域中都有广泛应用,比如在制定工程安全标准和评估金融风险时。二是测量的集中性。这是概率论中的一个关键概念,指的是大量独立随机变量的函数往往会以高概率接近它们的均值。Talagrand在这一领域的工作为高维统计问题的非渐近独立性理论奠定了基础。这个概念在数据科学和机器学习中非常重要,因为它帮助我们知道在大数据集中,大多数数据点通常会聚集在某个中心值附近,从而可以更准确地估计总体参数。三是自旋玻璃态。这是一种特殊的物质形式,其原子可以自我排列。自旋玻璃态的研究对于理解无序系统中的复杂行为至关重要。Talagrand在自旋玻璃态的研究中做出了重要贡献,特别是在证明自由能的帕里西公式方面。这个领域的研究不仅有助于我们理解物质的性质,还可以应用于优化算法和人工智能领域,以寻找最优解或最小化能量函数。 Talagrand的工作不仅对数学领域产生了深远影响,也对物理学、统计学、计算机科学等多个学科产生了重要影响。他的研究帮助我们从更深层次理解随机性,并在实际应用中提供了重要的理论工具。 |
|
阿贝尔奖(Abel Prize)是挪威设立的国际数学界年度奖项之一。 |
|
|
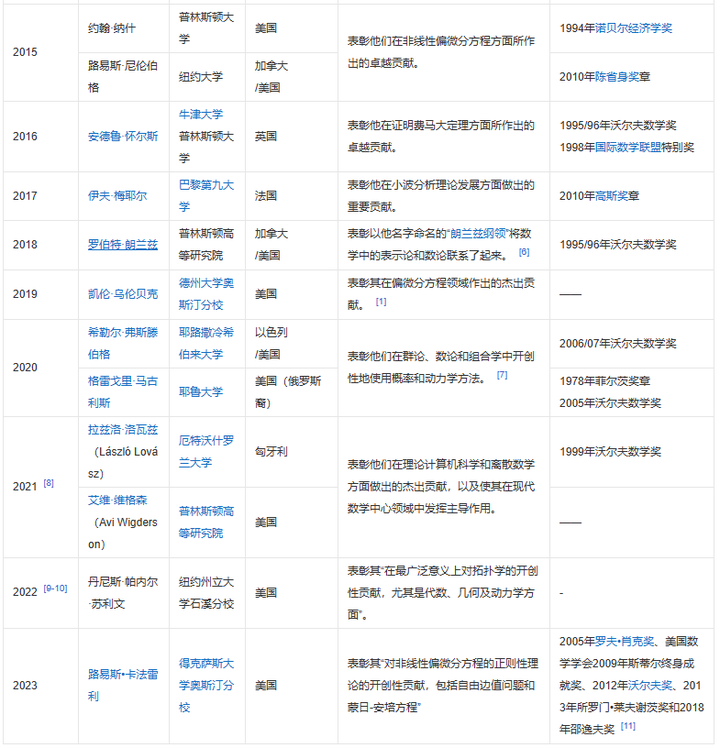
2001年,为了纪念挪威著名数学家尼尔斯·亨利克·阿贝尔二百周年诞辰,挪威政府宣布将开始颁发此奖,并拨款2亿挪威克朗作为启动资金。 自2003年起,一个由挪威自然科学与文学院的五名数学家院士组成的委员会负责宣布获奖人。 奖金的数额大致同诺贝尔奖相近,设立此奖的一个重要原因也是因为诺贝尔奖没有数学奖项。 因此,扩大数学的影响并吸引年轻人从事数学研究是设立阿贝尔奖的主要目的。 历届阿贝尔奖得主有: |

|
|
|
|
|
大部分工科和理科专业的同学都会学习概率论、随机过程等数学课程,在如今大火的人工智能领域,概率论也是其重要的数学基础,相信学过的人都不会不知道高斯过程。 |

|
|
Michel Talagrand的大部分工作都与随机过程的几何有关,他通过发展通用链式(Generic Chaining)理论,为高斯过程的上确界提供了清晰的上界和下界。 本次Michel Talagrand的获奖词为:“他在概率论和泛函分析方面的开创性贡献,以及在数学物理和统计方面的杰出应用。” |

|
|
|

|
|
本届阿贝尔奖的更多信息: 颁奖仪式将于2024年5月21日在挪威的首都奥斯陆举行;阿贝尔奖由挪威政府资助,金额为750万挪威克朗 (约511万人民币);该奖项由挪威科学与文学学院颁发,并由国王哈拉尔五世亲自颁奖;阿贝尔奖得主的选择基于阿贝尔委员会的推荐,该委员会由五名国际公认的数学家组成。 |
|
从随机性中创造了秩序。 说白了,我们倾向于觉得数学处理的是明确固定的不可变的事物。 但是在Talagrand研究的是:如何用数学去处理我们所生活自然界里充满的随机现象。 各种随机过程都表现出了一定的规律性。 在Talagrand 的大部分研究工作里边儿,都涉及到了了高斯分布。哎呀其实就是正态分布或者说钟形曲线啦——它能描述变量值分布在均值周围的概率分布。 高斯概率分布可太普遍啦——它的应用相当广泛,无数生活里边的现象都遵循高斯分布,身高、体重、血压值…… |
|
|
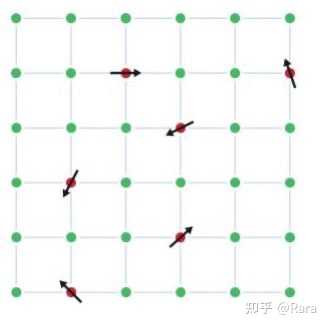
不同现象的高斯分布曲线的平均值和宽度都会有所不同,但曲线的整体形状以及描述它的数学公式将是相同的。 对于所选择的几乎任何随机样本,只要样本量足够大,直方图都将近似高斯钟形曲线。 我们可以用它来研究随机性对我们日常生活的影响。 上面人群身高的例子是一个随机变量,但高斯过程可以描述了存在许多(可能是无限多个)随机变量的情况——每个随机变量都遵循正态分布,并且可以以某种方式相关。 比如在许多不同时间点测量空气中污染物的浓度。每个单独测量的可能结果可能遵循正态分布,并且在时间上彼此接近的测量可能会相似。 知道可以使用高斯过程的数学概念来描述这种情况是很有用的哟。 比如它可以允许咱们计算测量在一定时间范围内的平均值。 除了平均值之外,还有一个:极端值——我们可以在高斯过程中看到的最大或最小值是多少? 极限边界确定的意义 反正Talagrand著名的泛型链理论以Xavier Fernique和Richard Dudley的研究结果为基础,可以给这些极值的大小提供一个明确的界限或者边界。 针对某一特定现象,极值的信息在做决策时可是相当重要的哦。 比如空气污染吧,如果预测到的极值很大,那就要加大力度应对空气污染啦。 测量集中性的意义 以概率论里经典赌博为例。当你掷一次骰子时,每个数字都有相同的 1/6 被掷出的概率。 1/6这个概念在只掷了一次骰子的情况下,会让人觉得很抽象。 但是当掷骰子 6000 次之后的数据可以告诉咱们,得到的 1 的数量最有可能在 1000 左右。这是因为有更多的 6000 次掷骰序列,其中大约有 1000 个 1(其他数字2到6也是如此。)。 这种见解是大数定律 的例证,非常有用哦。 比如开一家赌场(违法行为哈属于是),它可以帮助咱们预测在涉及投骰子游戏里边儿的长期收益或损失——虽然没办法预测单次游戏的结果。 当涉及到不像掷骰子这种结果范围很明确清晰的随机过程时,获得概率集中的结果要困难得多。 但Talagrand的研究工作却说明了:许多随机事件的相互作用会导致更可预测的结果,而且还给出了对于不确定性程度的估计。 关于自旋玻璃态相关研究的意义 鉴于统计学和概率论有着千丝万缕的联系,Talagrand对统计物理学也做出了重要贡献也就不足为奇啦。 自旋玻璃这种无序材料就是金属合金,其中一些铁原子混合到铜原子网格中。每个铁原子的行为就像一个微小的磁铁,也称为自旋,并受到附近其他铁原子的影响。 |
|
|
自旋玻璃是一种金属合金,其中(例如)铁原子(红色)随机混合到铜原子网格(绿色)中。每个铁原子的行为就像一个小磁铁或自旋,并受到附近铁原子的影响。 在普通磁铁中,所有自旋排列在一起指向同一方向,但在自旋玻璃中,一些自旋对想要指向同一方向,而其他对自旋想要指向相反方向。 那问题就来了,自旋如何找到最佳配置,使系统能量最小化呢? 然后Giorgio Parisi 在就提出了一个自旋玻璃系统自由能的公式——因此获得了21年的诺贝尔物理奖。 不过Parisi没有提供证明这个公式确实是正确的证据。 反倒是数学物理学家Francesco Guerra证明了自由能不可能比Parisi所提公式所建议的更大了。然后Talagrand也证明了它不能再小了。 要说起这个的意义,应该说影响远远超出了对自旋玻璃这种无序材料本身的研究了吧。 因为所涉及的数学完全可以应用于其他无序系统——毕竟我们周围的世界中可是有很多这样的系统。 比如说深度学习算法,而深度学习算法可是能推动人工智能的进步的哟! 数学往往取决于找到正确的观点:一旦找到了正确的观点,困难的想法就会突然变得简单! |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |