| |
|
|
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 自然科学 -> 如何证明4＞π＞3? -> 正文阅读 |
|
|
[自然科学]如何证明4＞π＞3? |
| [收藏本文] 【下载本文】 |
|
如何证明4＞π＞3? 关注问题?写回答 [img_log] 数学 数论 π（圆周率） 高等数学 如何证明4＞π＞3? |
|
这样也可以： |
|
|
上上颜色就更直观一些： |
|
|
|
|
|
|
|
注意到： 0">4−π=∫014x21+x2dx>0" role="presentation">4?π=∫014x21+x2dx>0\displaystyle 4-\pi =\int_{0}^{1} \frac{4x^2}{1+x^2}\mathrm{d}x>0 0">π−3=∫0116x4(1+x2)(3+x2)2dx>0" role="presentation">π?3=∫0116x4(1+x2)(3+x2)2dx>0\displaystyle \pi -3=\int_{0}^{1} \frac{16x^4}{(1+x^2)(3+x^2)^2}\mathrm{d}x>0 得证！ 自己作了一个“帕德近似表”的程序很吃香[滑稽] |
|
|
4和3恰好对应 4arctan⁡x" role="presentation">4arctan?x4\arctan x 的1阶 Taylor" role="presentation">Taylor\text{Taylor} 展开和 [1,2]" role="presentation">[1,2][1,2] 阶 Pade" role="presentation">Pade\text{Pade} 近似 |
|
证：3=6sin⁡π6<π<4tan⁡π4=4.◻" role="presentation">3=6sin?π6<π<4tan?π4=4.?3=6\sin\frac\pi63=6\sin\frac\pi6<\pi<4\tan\frac\pi4=4.\qquad\square\\ |
|
π的定义为圆形周长与直径之比，割圆法秒了 |
|
注意到积分 ∫01x1+xdx" role="presentation">∫01x1+xdx\int^{1}_{0}\frac{\sqrt{x}}{1+x}\mathrm{d}x ，置 x=t2" role="presentation">x=t2x=t^2 ∫01x1+xdx=2∫01t21+t2dt=2−2∫01dt1+t2=2−2arctan⁡1=2−π2" role="presentation">∫01x1+xdx=2∫01t21+t2dt=2?2∫01dt1+t2=2?2arctan?1=2?π2\begin{align} \int_{0}^{1}\frac{\sqrt{x}}{1+x}\mathrm{d}x=2\int_{0}^{1}\frac{t^2}{1+t^2}\mathrm{d}t=2-2\int_{0}^{1}\frac{\mathrm{d}t}{1+t^2}=2-2\arctan{1}=2-\frac{\pi}{2} \end{align} 于是 0 \end{align}">4−π=2∫01x1+xdx>0" role="presentation">4?π=2∫01x1+xdx>0\begin{align} 4-\pi=2\int_{0}^{1}\frac{\sqrt{x}}{1+x}\mathrm{d}x>0 \end{align} |
|
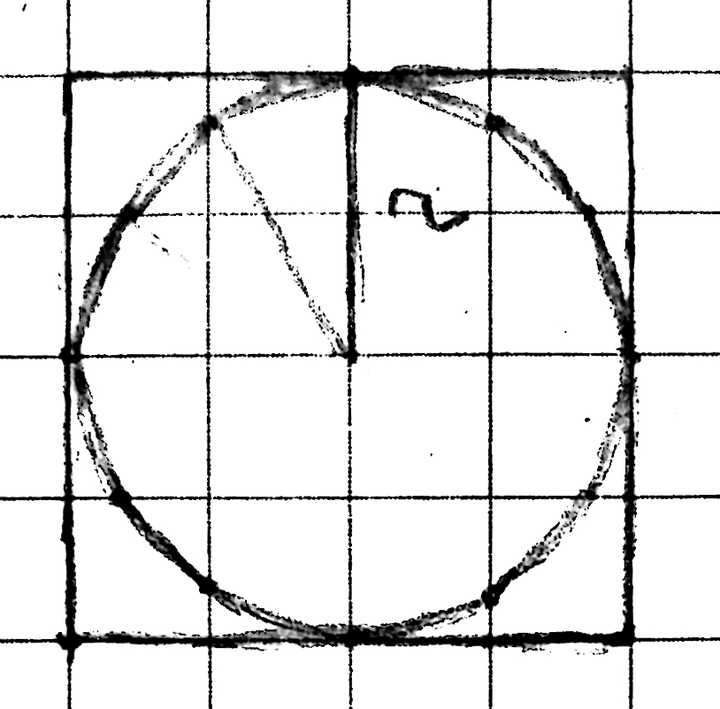
用面积的方法也可以证明。 作半径为 r" role="presentation">rr 的圆的内接正十二边形和外切正方形。 |
|
|
则正方形的面积 Ssquare=4r2" role="presentation">Ssquare=4r2S_{\rm square}=4r^2 , 正十二边形的面积 S12−gon=3r2" role="presentation">S12?gon=3r2S_{12 \rm-gon}=3r^2 . ∵" role="presentation">∵\because 圆的面积 Scircle=πr2" role="presentation">Scircle=πr2S_{\rm circle}=\pi r^2 ，又 S12−gon<Scircle<Ssquare" role="presentation">S12?gon<Scircle<SsquareS_{12\rm-gon}<S_{\rm circle}<S_{\rm square} , ∴3<π<4" role="presentation">∴3<π<4\therefore 3\therefore 3<\pi<4 . 以上。 |
|
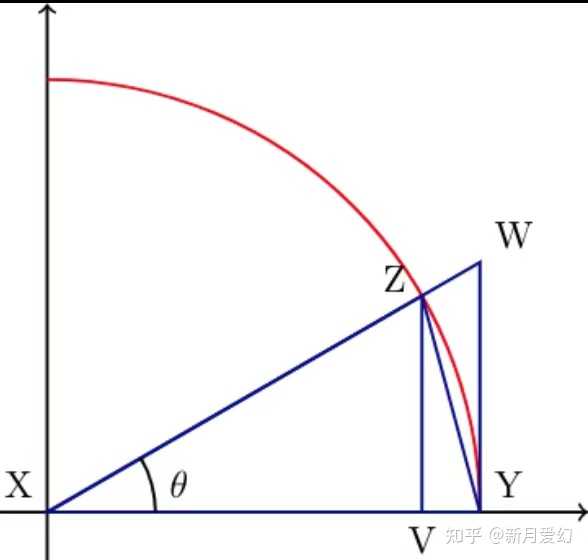
利用三角函数性质 sinθ<θ<tanθ" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">sinθ<θ<tanθsin\thetasin\theta<\theta<tan\theta\\ |
|
|
根据上述性质有 12<sinπ6<π6<tanπ6=33" role="presentation" style="font-size: 100%; display: inline-block; position: relative;">12<sinπ6<π6<tanπ6=33\frac{1}{2}\frac{1}{2}<sin\frac{\pi}{6}<\frac{\pi}{6}<tan\frac{\pi}{6}=\frac{\sqrt3}{3}\\ 则有 3<π<23＜2⋅2=4" role="presentation">＜3<π<23＜2?2=433<\pi<2\sqrt{3}＜2\cdot2=4 。 |
|
由 3.1415926<π<3.1415927 （证明见祖冲之） 得 4>π>3 |
|
attention is all you need |
|
|
|
|
不太严格的证明：圆内接一个正六边形，证明大于3；外接一个正方形，证明小于4。 |
|
你乎没活了，这都能热搜第三 |
|
如果你不知道π约等于3.14，这道题等价于求圆周率第一位，请参如何算圆周率， 如果你知道，那就不用证了。 |
|
注意到 3<x<4" role="presentation">3<x<4x=\pi 显然： 3<π<4" role="presentation">3<π<44>\pi>3 |
|
4>π=3.1415926...>3 不然呢~ |
|
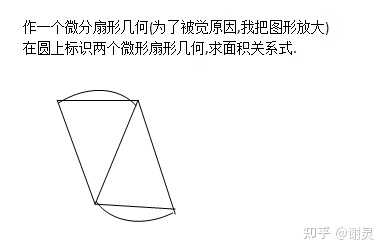
应用几何图形方法。 π" role="presentation">ππ 定义：单位圆的周长。 几何和代数证明了圆面积公式： 圆面积 ＞π×r×r" role="presentation">＞＞π×r×r＞π×r×r |
|
|
两个扇形面积大于两个三角形面积. 扇形顶角 θ" role="presentation">θθ ,一个扇形面积 s1" role="presentation">s1s_{1} , 一个三角形面积: 12×sinθ×r×r" role="presentation">12×sinθ×r×r\frac{1}{2}\times sinθ\times r\times r ,注明: h=sinθ×r" role="presentation">h=sinθ×rh=sinθ\times r , h" role="presentation">hh 是三角形 r" role="presentation">rr 边上的高. 只有扇形顶角为 0" role="presentation">00 时,两个扇形面积 =" role="presentation">== 两个三角形面积 =0" role="presentation">=0=0 『两个扇形面积扩成 n" role="presentation">nn 个扇形就是圆面积 S" role="presentation">SS : S=n×s1" role="presentation">S=n×s1S=n\times s_{1} , 扇形弧总和就成了单位圆周长: n×sinθ×r=π(n→∞,θ→00)" role="presentation">n×sinθ×r=π(n→∞,θ→00)n\times sin\theta \times r=π(n\rightarrow\infty,\theta\rightarrow0^{0}) 因为微积分原理: 12=r," role="presentation">12=r,\frac{1}{2}=r, n×12×sin0×r×r=πr2" role="presentation">n×12×sin0×r×r=πr2n\times\frac{1}{2}\times sin0\times r\times r=πr^{2} , 唯一性相等: 扇形面积=三角形面积=0 唯一性相等机会: 圆面积= πr2=0" role="presentation">πr2=0πr^{2}=0 』 特殊情况 r＝0" role="presentation">＝r＝0r＝0 时，圆面积 ＝π×r×r＝0。" role="presentation">＝＝。＝π×r×r＝0。＝π×r×r＝0。 所以,上图证明了:圆面积 ＞π×r×r" role="presentation">＞＞π×r×r＞π×r×r 因为圆的相似性，做一个半径 r＝1" role="presentation">＝r＝1r＝1 的圆，其直径 ＝2" role="presentation">＝＝2＝2 。 此时的圆面积 ＞π×1×1＝π" role="presentation">＞＝＞π×1×1＝π＞π×1×1＝π 第一步：用面积法证明 4＞π" role="presentation">＞4＞π4＞π 做此圆的外接正方形，它的面积必然是4。 所以证明了 4＞" role="presentation">＞4＞4＞ 圆面积 ＞π" role="presentation">＞＞π＞π 第二步：周长法证明 π＞3 接下来在单位圆中做内接六边形，其边长为 1／2 ，六边形周长 ＝3 因为公理两点之间直线最短,所以:曲线弧 ＞ 直线弦。 所以，这个单位圆周长π＞3 证明了： 4＞π＞3 |
|
对于边长为2的正方形，面积为4； 对于边长为2的正方形，其内切圆面积为π； 对于边长为2的正方形，其内切圆中内接正十二边形面积为3。 所以4＞π，π＞3。 |
|
半径为1的圆内接正六边形求出圆周率的下限为3，再用外接正六边形并借助勾股定理求出圆周率的上限为4。 |
|
直接搬出泰勒展开 不用几何直接代数 pi = 4 arctan（1） = 4（1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ……） = 4 - 4/3 + 4/5 - 4/7 +4/9 - 4/11 + …… 因为 （-4/3 + 4/5）和（-4/7 + 4/9）这些项都小于0 所以原式小于4 然后把原式一项一项往后算计算 可以得到 = 3.01707182 + 4/17 - 4/19 +…… 因为（4/17 -4/19）以及后面的项都大于0 iNNe">所以原式大于3.01707182，也就是大于3 |
|
画一个直径为1的圆，它的周长是π 用尺子分别量出两根长度为3和4的线，往这个圆上套，长3的不够，长4的有富裕 证毕 |
|
|
| [收藏本文] 【下载本文】 |
| 自然科学 最新文章 |
| 海南一村民被眼镜王蛇咬死，多名消防员和村 |
| 有哪些不起眼的牢底坐穿兽？ |
| 美国耕地面积比中国大，可为什么粮食产量不 |
| 如何看待同济大学2024国家科技三大奖颗粒无 |
| 假如航母被蓝鲸全速前进撞一下会怎么样？ |
| 你见过最狠的SCI评论是什么? |
| 你在实验室最惊险的瞬间是什么？ |
| 牛顿生活在中国，会有什么成就？ |
| 虎鲸为什么不吃人？ |
| 数学为什么这么可笑？ |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |