| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 为什么欧拉常数e在物理学公式中不常见到? -> 正文阅读 |
|
|
[时尚穿搭]为什么欧拉常数e在物理学公式中不常见到? |
| [收藏本文] 【下载本文】 |
|
为什么欧拉常数e在物理学公式中不常见到? 关注问题?写回答 [img_log] 物理学 数学物理方法 物理公式 为什么欧拉常数e在物理学公式中不常见到? |
|
这个问题出现在我首页好几次了……翻了一圈回答和评论,发现题主想问的并不是“为什么e在物理学中不常见”,而是“为什么e在题主学过的物理学中不常见“。 那原因很简单:因为高中物理是被精心删减过的,和e相关的都被删去了。而之所以这么删减,是因为高中数学不讲微分方程。 所有答主都提到了e在物理学中几乎无处不在,它的本质原因是: 几乎所有的物理定律都是微分方程e会自然地出现在线性微分方程的解当中人类能求解的微分方程大部分都是线性微分方程 第一点的原因其实很简单:因为大部分物理学描述的都是各种意义上的“运动”,也就是描述物理量随时间的变化,这个“变化”就是微分。还有一些描述物理量在空间中的分布,也就要刻画物理量在空间中的变化,这也是微分。 但由于高中数学教学的限制,高中物理刻意淡化了这一点,把教学内容限制在可以用初等数学处理的范围内。事实上,高中物理学到的东西,几乎都要用微分方程来表示。最简单的,牛顿定律里的加速度是位移的二阶导数,凡是写了牛顿第二定律的都是微分方程。剩下的例子也数不胜数:电场和电势的关系、电磁感应定律、振动和波、放射性元素衰变律…… 而题主之所以没有在这些公式里面看到e,是因为教材选取的都是不需要求解微分方程就可以理解的。所以你不会学到如何求解一个正比于速度的空气阻力、不会学到阻尼振动的振幅衰减、不会学到一个线圈中的电流在电磁感应的作用下会如何演变……这几个例子还是最初等的,还有很多在物理学中非常基础、但是因为“不能用微分方程“在高中物理中被完全删去的,比如麦克斯韦方程或者更广义的波动方程。 总的来说,e在高中物理中确实不常见,但这是高中教学大纲刻意安排的结果,而不是物理学本身如此。 |
|
这提问者挺虚心求学的。 |
|
|
|

|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
因为题主提问的态度恶劣,不幸被一群不耐烦的网友用一具有弹性的绳子吊在了一根坚固路灯上,如下图所示。此时,题主摇身成为了一道高中物理题目。 |
|
|
被挂路灯的题主 其中题主的质量为 m,并且受牛顿第二定律支配: F题主=ma=md2xdt2" role="presentation">题主F题主=ma=md2xdt2\begin{align} F_\text{题主} = ma = m \frac{d^2x}{dt^2} \end{align} 绳子的弹性系数为 k,并且受胡克定律支配: F绳子=kx" role="presentation">绳子F绳子=kx\begin{align} F_\text{绳子} = kx \end{align} 摩擦力创造了阻尼系数 c。在理想模型中,一般假设摩擦力的唯一来源是我们人为加入的线性阻尼器,因此其阻力与速度成正比(如果是空气阻力,这个近似只适用于低速小物体): F阻尼=cv=cdxdt" role="presentation">阻尼F阻尼=cv=cdxdt\begin{align} F_\text{阻尼} = cv = c \frac{dx}{dt} \end{align} 此时,一位暴徒将题主向下拽了一下并松手,题主开始摆动(因为题主是一个一维生物,因此只能上下摆动)。此时整个系统不再受外力,其运动方程可以写为: F题主+F阻尼+F绳子=0md2xdt2+cdxdt+kx=0" role="presentation">题主阻尼绳子F题主+F阻尼+F绳子=0md2xdt2+cdxdt+kx=0\begin{align} F_\text{题主} + F_\text{阻尼} + F_\text{绳子} &= 0 \\ m \frac{d^2x}{dt^2} + c \frac{dx}{dt} + kx &= 0 \end{align} 解方程后可以发现,题主位置函数的一般形式为: x(t)=Ae−ωnt(ζ+ζ2−1)+Be−ωnt(ζ−ζ2−1)" role="presentation">x(t)=Ae?ωnt(ζ+ζ2?1)+Be?ωnt(ζ?ζ2?1)\begin{align} x(t) = A \mathrm{e}^{-\omega_\text{n} t \left(\zeta + \sqrt{\zeta^2-1}\right)} + B \mathrm{e}^{-\omega_\text{n} t \left(\zeta - \sqrt{\zeta^2-1}\right)} \end{align} 其中, ωn" role="presentation">ωn\omega_\text{n} 是自然频率: ωn=km" role="presentation">ωn=km\begin{align} \omega_\text{n} = \sqrt{k \over m} \end{align} 而 ζ" role="presentation">ζ\zeta 是阻尼比: ζ=c2mωn" role="presentation">ζ=c2mωn\begin{align} \zeta = \frac{c}{2 m \omega_\text{n}} \end{align} 当 ζ=0" role="presentation">ζ=0\zeta = 0 时,题主不受任何阻尼,会永远上下横跳;当 0<ζ<1" role="presentation">0<ζ<1\zeta > 1 时,题主处于过阻尼状态。此时题主直接向原位单调地移动,不会反复上下振荡,但需要被弹簧拉伸很长时间才能缓慢回到原位;当 ζ=1" role="presentation">ζ=1\zeta = 1 时,题主处于临界阻尼状态。此时题主会以最短时间干净利索的回到原位。 |

|
|
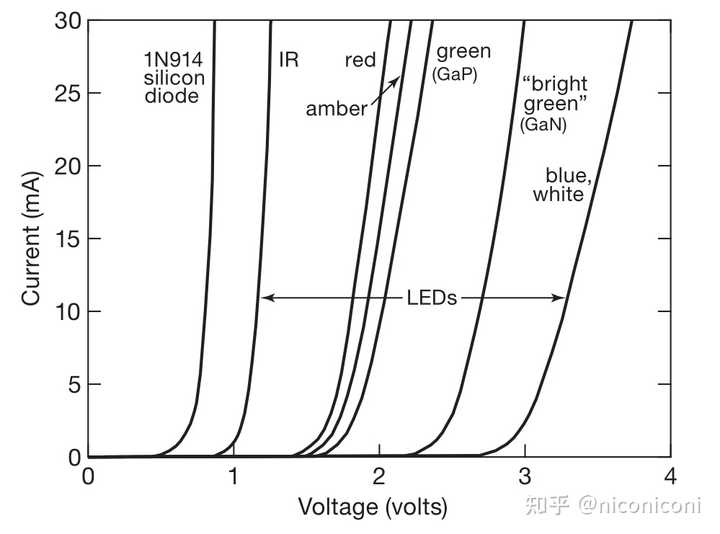
不同阻尼比时的振荡波形 经历过这次事件后,题主顺着网线破口大骂。含有骂人内容的电子信号,是由题主计算机内的集成电路中的一个输出级电路产生的。在集成电路中,无数个 P 型与 N 型半导体相互连接,从而形成了二极管与三极管。由于 P-N 结是非线性的,它不遵守欧姆定律,而是受到肖克利二极管方程的支配: ID=IS(eVDnVT−1)" role="presentation">ID=IS(eVDnVT?1)\begin{align} I_\text{D} = I_\text{S} \left( \mathrm{e}^\frac{V_\text{D}}{n V_\text{T}} - 1 \right) \end{align} 方程中, VD" role="presentation">VDV_\text{D} 、 ID" role="presentation">IDI_\text{D} 是二极管的电压与电流; VT" role="presentation">VTV_\text{T} 是热电压,在常温下约为 0.025 V;IS" role="presentation">ISI_\text{S} 是二极管饱和电流, n" role="presentation">nn 是理想因子。这两个为经验参数,需要通过实验测量得到。 因为肖克利二极管方程没有初等解,从这个基本原理直接求电路中二极管的电压、电流是非常困难的,需要朗伯 W 函数等高等数学知识。所幸,许多应用中也可以把这个令人恼火的 −1" role="presentation">?1-1 项丢弃,使它的解成为普通的对数方程。但还存在更简单的模型:注意到指数方程的增长是爆炸性的。在给 P-N 结施加的电压超过一个临界值后,电流就开始爆炸性增长——这也是为什么直接将二极管或 LED 灯连接在可调电源上,很快就会烧毁。相反,也可以说:如果我们逐渐加大二极管中的电流,起初电压越来越大,但是在超过一个临界值后就几乎不再发生变化。因此在工程技术中可以认为二极管的压降是固定的,硅二极管通常取 0.7 V,除此之外与短路没有区别。 |
|
|
二极管与 LED 的伏安曲线 当含有骂人内容的电子信号产生后,它会顺着集成电路内的微小导线传播。因为信号的传播速度有限,因此它也给出了题主骂人速度的上限。许多人都说芯片内的信号沿光速传播,但这是错误的。在电缆、光纤与电路板中,信号的传播速度的确接近光速(因为介质存在,实际约为真空光速的 1/2 到 2/3)。但集成电路内部尺度很小,传输线效应往往可以忽略。 此时芯片的导线可以视作一阶 RC 电路: |

|
|
一阶 RC 电路 其中,电容电压遵循以下方程: VC(t)=Vin(1−e−tRC)" role="presentation">VC(t)=Vin(1?e?tRC)\begin{align} V_\text{C}(t) &= V_\text{in} \left(1 - \mathrm{e}^{-\frac{t}{RC}} \right) \end{align} Vin 是电压源的电压;R 是导线的寄生电阻——由于集成电路中的导线很微小,因此电阻是不能忽略的;C 是导线与晶体管输入端的寄生电容——众所周知,任何两个由绝缘体分离的导体都是电容。而芯片中错综复杂的导线与晶体管,自然也会通过电场发生相互作用,因此电容效应是相当明显的;其中 RC 又称为系统的时间常数 τ=RC" role="presentation">τ=RC\tau = RC 。 导线的寄生电容通过寄生电阻充电、放电的速度,决定了电子信号在集成电路中最高传输速度。 |
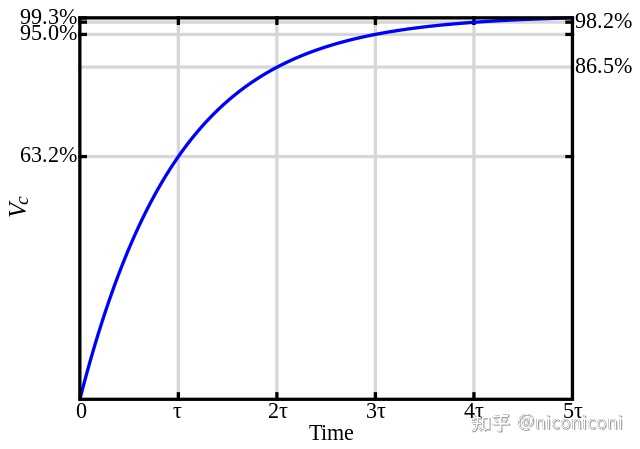
|
|
电容充电波形 因为指数函数不便口算,所以还有以下经验法则: 电容在 t=4τ" role="presentation">t=4τt = 4\tau 秒后几乎充满。信号的 10%-90% 上升时间为 trise=2.2τ" role="presentation">trise=2.2τt_\text{rise} = 2.2\tau 但是,尽管在上述知识与公式中都出现了 e,题主却认为这些物理学现象都不存在。最终,在题主自己所处的宇宙空间中,其物理法则并不允许发出任何电子信号,题主骂人的内容我们至今也从未收到过;同理,“挂路灯事件”也从未发生过。 |
|
? e在微分方程和物理学中的地位,就像x在方程里的地位。 题主是个高中生 不知道调和级数和真正的欧拉常数。其实要是在题干里说“高中生,为什么…”就不会看起来充满槽点了。 |
|
这我可得杠一下了,欧拉常数不是γ吗 |
|
常见,没有比e更容易出现在非理想环境的常数了。 你觉得不常见,是因为你遇到的问题都是理想环境。 这道题是自由落体,初速度为0加速度等于g,为什么不能用h=1/2gt方??www.zhihu.com/question/627268593/answer/3259940592?utm_psn=1706077743115067394 |

|
|
上的回答可以说完全适合你这个问题,如果是假设空气阻力恒定,和e无关(理想环境),如果空气阻力和速度有关,那么e就会出现。 不知道你能不能感受到,e代表了变化随着变化而变化而变化… 自然中的利滚利… |
|
确实不常见,因为它通常出现在物理公式的解里,而非公式里 |
|
你说得对,但如果我祭出配分函数以及基于配分函数和巨配分函数构建而成的前统计物理,阁下又该如何应对? |
|
首先,欧拉常数一般是指 γ≈0.577,是调和级数与自然对数差值的极限 其次,本来想举例的,但看另一个回答里举一个你就不知道一个,还是算了 |
|
你就不可能在任何一个物理领域里不常见到e,因为你就不可能离开微分方程聊物理 |

|
|
我相信你这个“钓鱼”的标签是认真的,如果是知乎自己加的,那说明官方也看不下去了 |
|
借地问个问题, Sigma 1/N 与ln N的差值的极限叫什么 我印象里也有个欧拉…但是我想不起来名字不知道怎么搜 |
|
可见您没怎么碰过热力学……玻尔兹曼熵、玻尔兹曼分布、阿伦尼乌斯方程,哪个没有自然对数的底? |
|
其实很常见,比如在统计力学里配分函数,图片百度百科找的 |

|
|
量子力学里解薛定谔方程也经常出现e 翻开一本桌上的物理书,里面的公式里也有一堆e |

|
|
|

|
|
|
|
题主如果认为“欧拉常数” e 在物理学里不常见,那可以提出一个以题主名字命名的“查勃多得了如是说常数”,要求不高,只要比 e 在物理学里出现得多就可以。如果题主找到了这么一个常数,那估计是发现了一个比微积分更重要的新数学分支,用题主的名字命名这个常数也不过分。 |
|
以 Euler 命名的数太多了……我还以为他说的是 Euler 常数 γ(Euler's constant, γ" role="presentation">γγ\unicode[Times]{x03B3} ),结果是 e(自然对数的底,Euler's number, e" role="presentation">e\mathrm e )吗? γ 的定义是调和级数与自然对数的差值: γ=limn→∞[(∑k=1n1k)−ln⁡n]≈0.5772" role="presentation">γγ=limn→∞[(∑k=1n1k)?ln?n]≈0.5772{\large\unicode[Times]{x03B3}}=\lim_{n\rightarrow\infty}\left[\left(\sum_{k=1}^n\frac1k \right)-\ln n \right]\approx0.5772\\ 就我学过的一点物理而言,γ 也是出现过的,不过远没有 e 频繁就是了[1].比如弱耦合 Bardeen-Cooper-Schrieffer(BCS)理论的零温能隙 \mathit\Delta_0 与临界温度 T_\mathrm c 的关系中,就包含了 γ: \frac{\mathit\Delta_0}{k_\mathrm BT_\mathrm c}={\large\unicode[Times]{x03C0}}\mathrm e^{-\color{red}{\large\unicode[Times]{x03B3}}}\approx1.764\\其中 k_\mathrm B 是 Boltzmann 常数;这个值经常被称作 BCS 比值.非常规超导(非 s 波超导)里这个值会偏离于 1.764. 任意有限温度 0<T<T_\mathrm c 下的能隙 \mathit\Delta(T) 则由以下自洽方程给出, \ln\frac{\mathit\Delta_0}{\mathit\Delta(T)}=2{w\left(\frac{\mathit\Delta(T)}{T}\right)}\tag{1}\\其中 w(a) 是个纯数学函数,其定义: w(a)=\int_1^\infty\frac{\mathrm dx}{(\mathrm e^{ax}+1)\sqrt{x^2-1}}\\接近临界温度即 T\rightarrow T_\mathrm c 时, \mathit\Delta\rightarrow0 ,相应的 w(a) 展开为: w(a)\simeq\frac{1}{2}\ln\frac{{\large\unicode[Times]{x03C0}}\mathrm e^{-\color{red}{\large\unicode[Times]{x03B3}}}}{a}+\frac{7{\large\unicode[Times]{x03B6}}(3)}{16{\large\unicode[Times]{x03C0}}^2}a^2\\其中 {\large\unicode[Times]{x03B6}}(x) 是 Riemann zeta 函数……代入后得到 T\rightarrow T_\mathrm c 极限下,能隙约为: \frac{\mathit\Delta(T)}{\mathit\Delta_0}\simeq \mathrm e^{\color{red}{\large\unicode[Times]{x03B3}}}\sqrt{\frac{8}{7{\large\unicode[Times]{x03B6}}(3)}\left(1-\frac{T}{T_\mathrm c}\right)}\approx1.737\sqrt{1-\frac{T}{T_\mathrm c}}\\ 反正我就是想说做某些近似的时候 γ 还是会出现的,而且经常跟 e 一起出现…… 有空再更 Ising 超导下上临界场 H_\mathrm{c2}(T) 的某个公式,也带 γ(不过这些感觉都是只有做实验的感兴趣,天天在做拟合……) 参考^以下内容抄自冯济老师的《固体理论》讲义。 |
|
涉及到一阶微分方程,频率,三角函数,量子力学,统计力学的,全都是。 |
|
什么时候e叫欧拉常数了 |
|
看到这个问题说实话挺震惊的,因为我天天见到哈哈哈。 在微分方程理论里面,特别是线性微分方程里面exp通常被当做基底,然后基底的线性组合就是通解,然后还要再加上一个特解。 在系统分析里面,傅立叶变换也要用到exp作为一个个频率分量的表示,再把她们加权求和变成原信号,这样就可以算出信号的频谱。其实这玩意和微分方程理论也是有关系的,一个连续时间的线性系统他就是一个线性的微分方程,然后我们可以用傅立叶变换把她变到频域分析,然后解出来之后再做逆变换回来时域,这里面到处都是exp。 在统计物理里面,exp也有很大的作用,比如麦克斯韦玻尔兹曼分布里面就有一个exp项。对这玩意积分要用高斯积分或者伽马函数。 在概率论和随机过程里面也处处可见这玩意,比如高斯分布里面就有exp项,其他也有很多分布都含有这玩意。 |
|
菜 就多练 学的少就多学 没见过是没见过 不存在是不存在 哥们 你把没见过当不存在 你怎么不去学唯心主义哲学啊 |

|
|
|
|
|
|

|
|
|
|
|
|
|
不知道为什么会提出这样的问题,既然知道欧拉常数e,那么应该知道欧拉公式。三角函数在物理学公式中很常见,凡是有三角函数相关的都可以有e。只是中学物理不学相关物理公式,都是定性或者半定量讨论问题。振动和波可以有e,电路分析、交变电流可以有e,…… |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |