[自然科学] 有哪些观赏性很高的几何图形？

天天财汇购物网址万年历小说 | 三峰软件小游戏视频

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

首页淘股吧股票涨跌实时统计涨停板选股股票入门股票书籍股票问答分时图选股跌停板选股 K线图选股成交量选股 [平安银行]

股市论谈均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

商业财经科技知识汽车百科工程技术自然科学家居生活设计艺术财经视频游戏--

天天财汇 -> 自然科学 -> 有哪些观赏性很高的几何图形？ -> 正文阅读

[自然科学]有哪些观赏性很高的几何图形？

[收藏本文] 【下载本文】

最近对神经系统有关审美的意识性问题感兴趣，我认为流行的审美观很容易就被扭曲，而自然存在的数学规律的图形表示最本质的符合人的审美是难以动摇的。希望在此有…

极小曲面就很具有观赏性，比如：
\mathit{1.}悬链面花瓶曲面

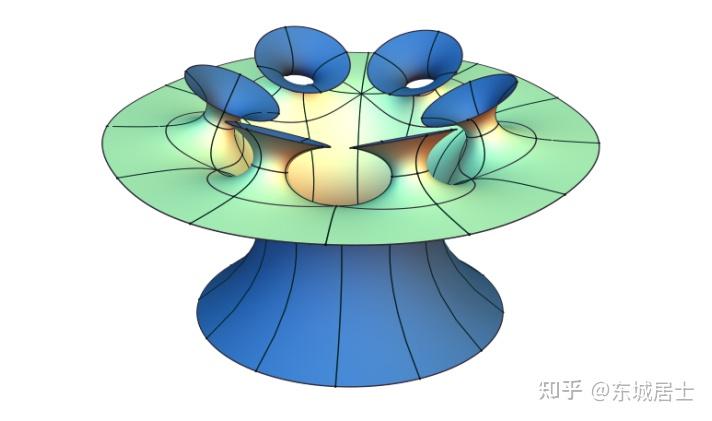
\mathit{2.} Enneper 曲面

\mathit{3.} Jorge-Meeks 曲面

\mathit{4.} Scherk 曲面

\mathit{5.} Karcher-Scherk 曲面

\mathit{6.} Chen-Gackstatter 曲面

\mathit{7.} Riemann 极小曲面

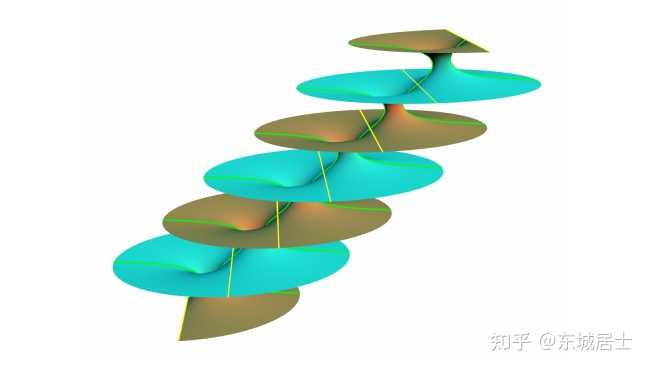
\mathit{8.} Costa 曲面

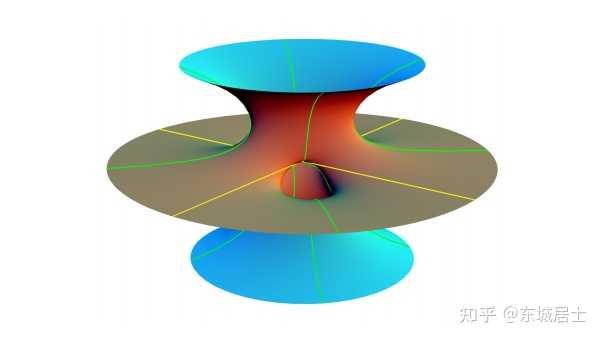
\mathit{9.} Callahan-Hoffan-Meeks 曲面

\mathit{10.} 叫不出名字的曲面

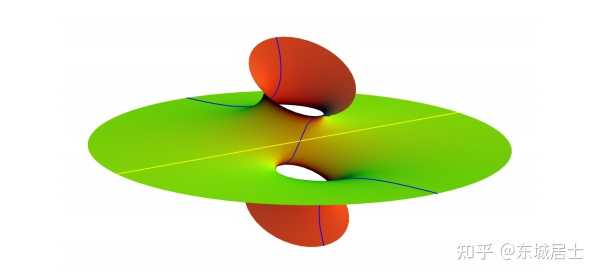
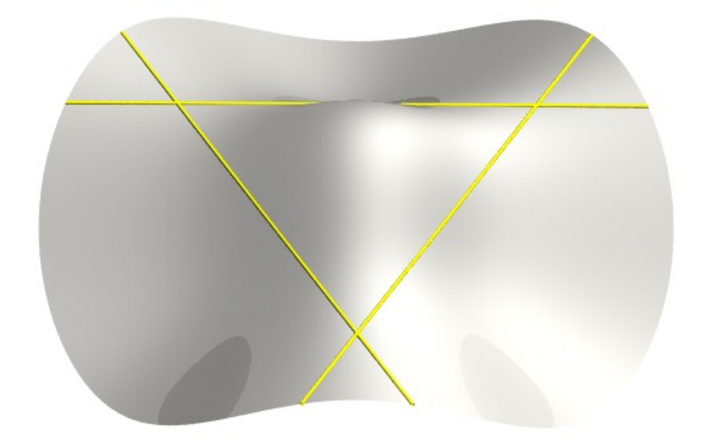
来点代数几何？
1858年，Schl?fli 证明了定义在实数域上的三次光滑曲面上恰好包含3、7、15或者27条实直线。
①恰好包含3条实直线的三次光滑曲面：
\large x^3+y^3+z^3=a^3\\

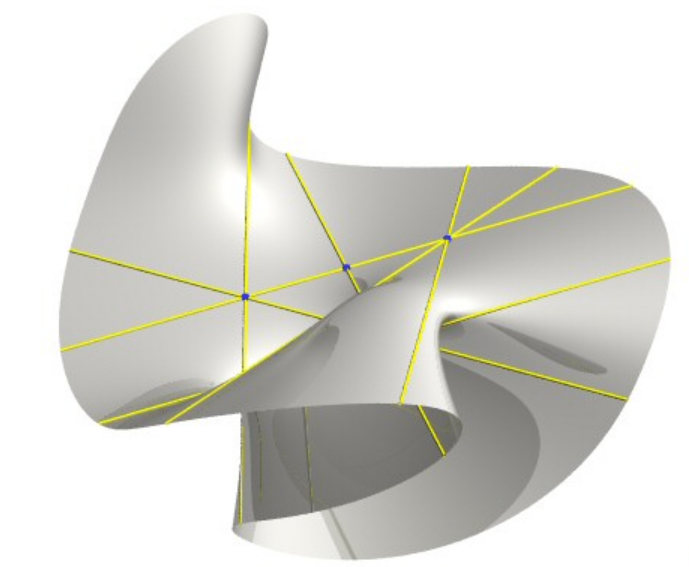
https://mathcurve.com/surfaces/cubic/cubic.shtml
②恰好包含7条实直线的三次光滑曲面：
\large xyz=a(x^2+y^2-z^2)+a^3\\

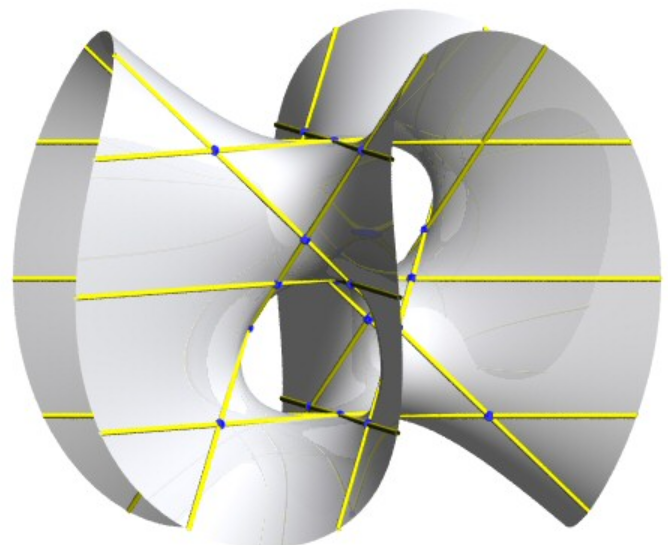
https://mathcurve.com/surfaces/cubic/cubic.shtml
③恰好包含15条实直线的三次光滑曲面：
\large z(z^2-a^2)=x(x^2-3y^2)\\

https://mathcurve.com/surfaces/cubic/cubic.shtml
④恰好包含27条实直线的三次光滑曲面：
Clebsch对角曲面。定义在复数域上的三次光滑曲面上恰好包含27条直线，这个曲面在复数域也没有多余的直线了。

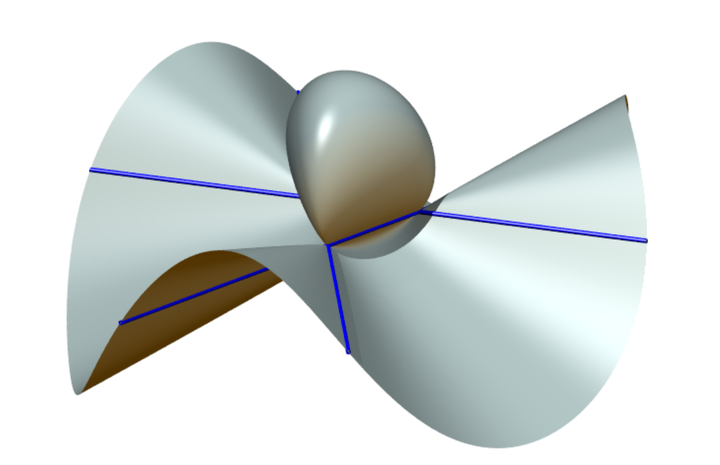
https://mathcurve.com/surfaces/clebsch/clebsch.shtml
Henrici三次曲面实际也有27条实直线，只是图像上的每条直线都是九条重合直线
\large xyz=k(x+y+z-a)^3\\

https://mathcurve.com/surfaces/cubic/cubic.shtml
一个定义在复数域上的三次曲面最多有4个Ordinary Double Point，
含有4个Ordinary Double Point的曲面：
Cayley三次曲面，其中含有4个实的Ordinary Double Point例子：

https://zhuanlan.zhihu.com/p/380608698

https://mathworld.wolfram.com/
一个定义在复数域上的四次曲面最多有16个Ordinary Double Point，
含有16个Ordinary Double Point的曲面：
Kummer曲面，其中含有16个实的Ordinary Double Point例子：

https://mathcurve.com/
一个定义在复数域上的五次曲面最多有31个Ordinary Double Point，
含有31个Ordinary Double Point的曲面：
dervish

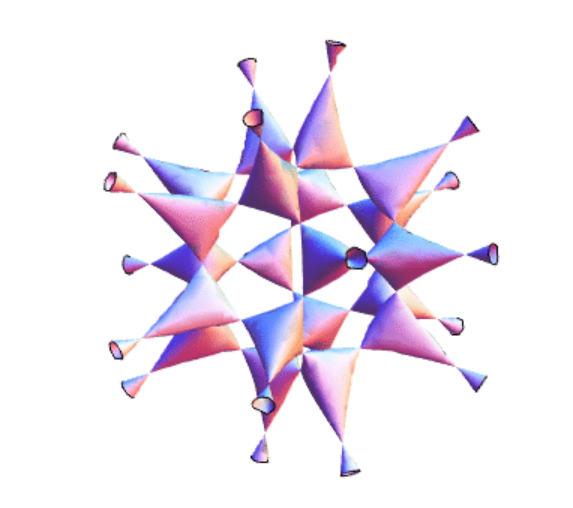
https://mathworld.wolfram.com/
一个定义在复数域上的六次曲面最多有65个Ordinary Double Point，
含有65个Ordinary Double Point的曲面：
Barth六次曲面

https://mathworld.wolfram.com/

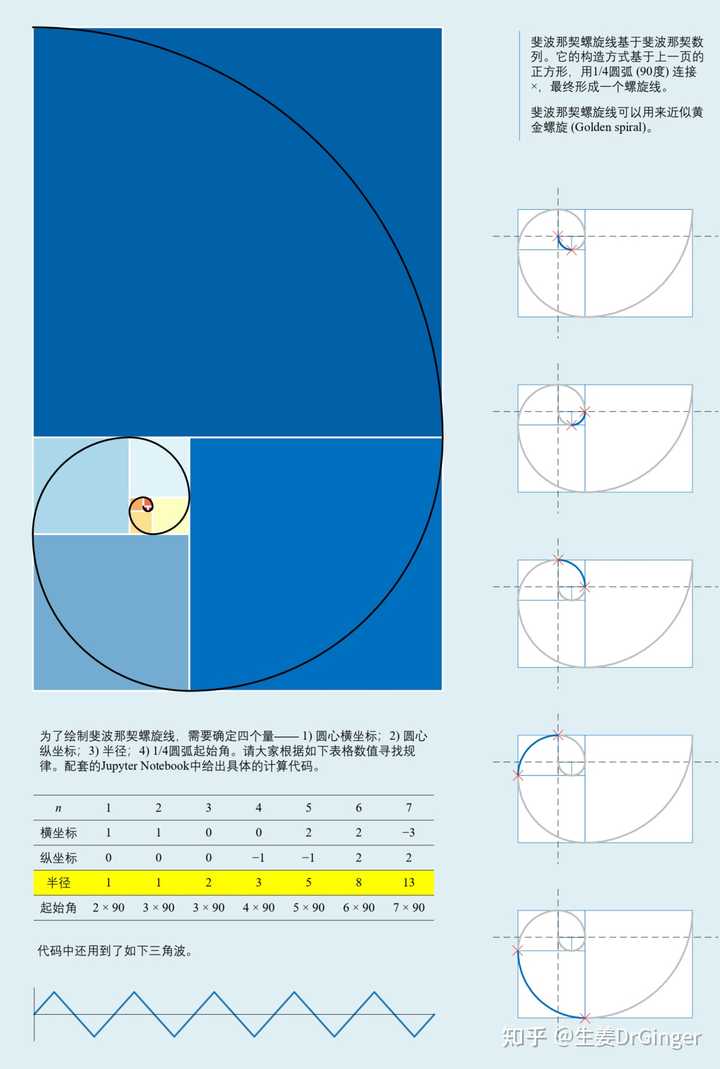
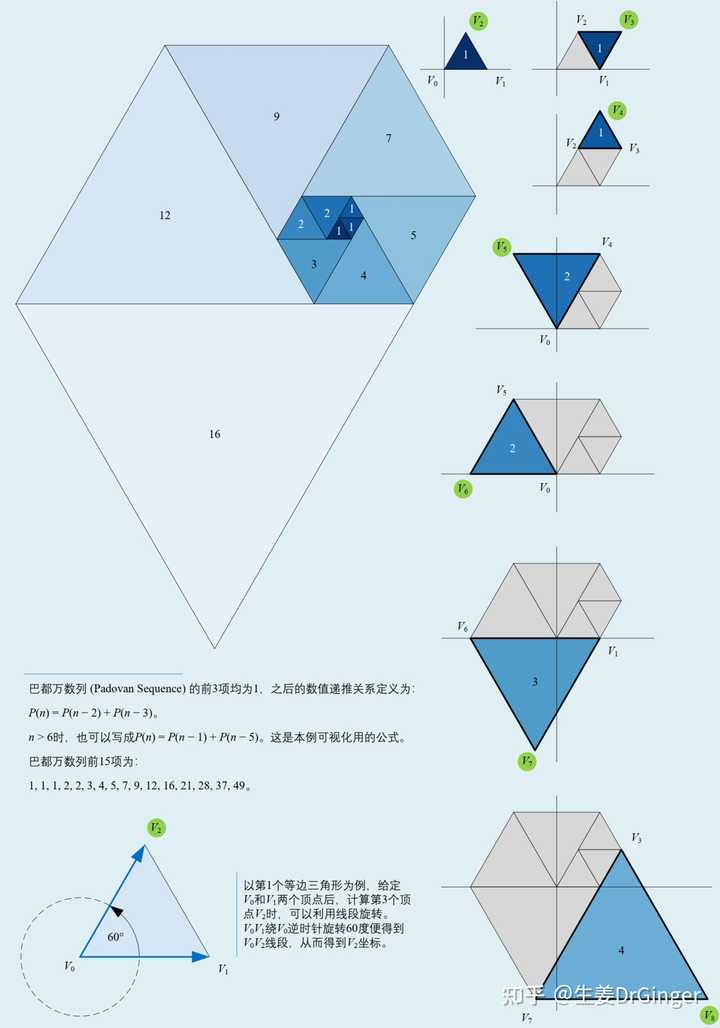
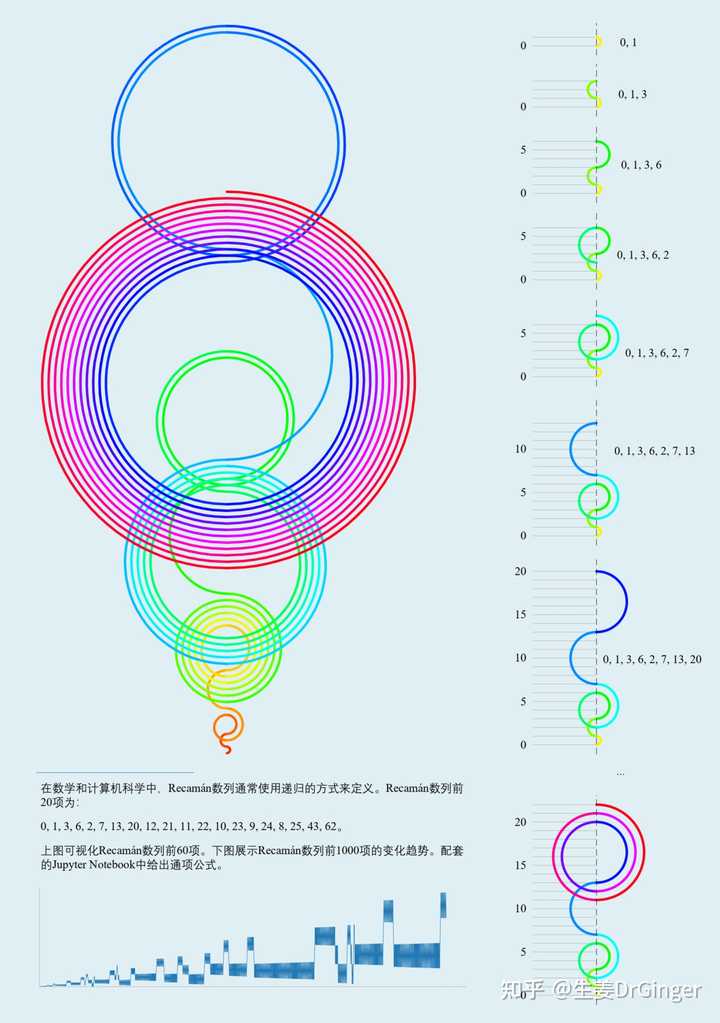
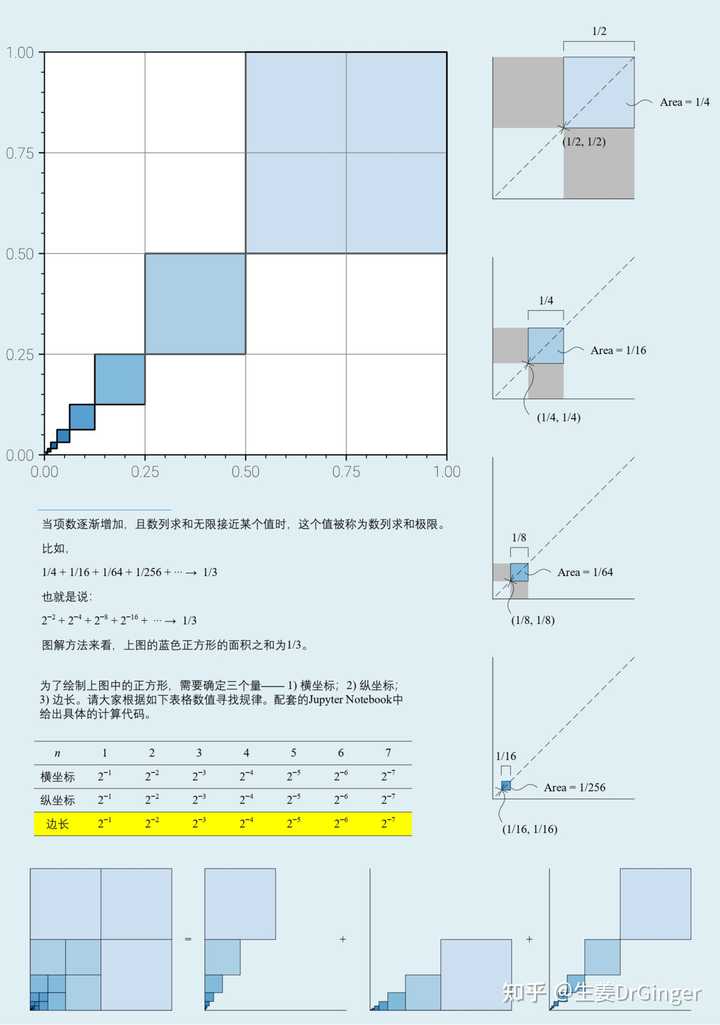
提到几何之美、数学之美，鄙人可就支棱起来了；因为，俺有一个小册子《可视之美》，就是和大家一起用Python进行创意编程可视化数学之美。下面从《可视之美》挑几（十）幅给大家。《可视之美》全书600+页书稿、500+图像、100+Python代码全部开源！
以上/以下，所有图，《可视之美》都有Python代码实现，欢迎拉上三五好友白嫖！
矢量图，大家就要移步Github了。
数列，用几何可视化手段展示数列和极限

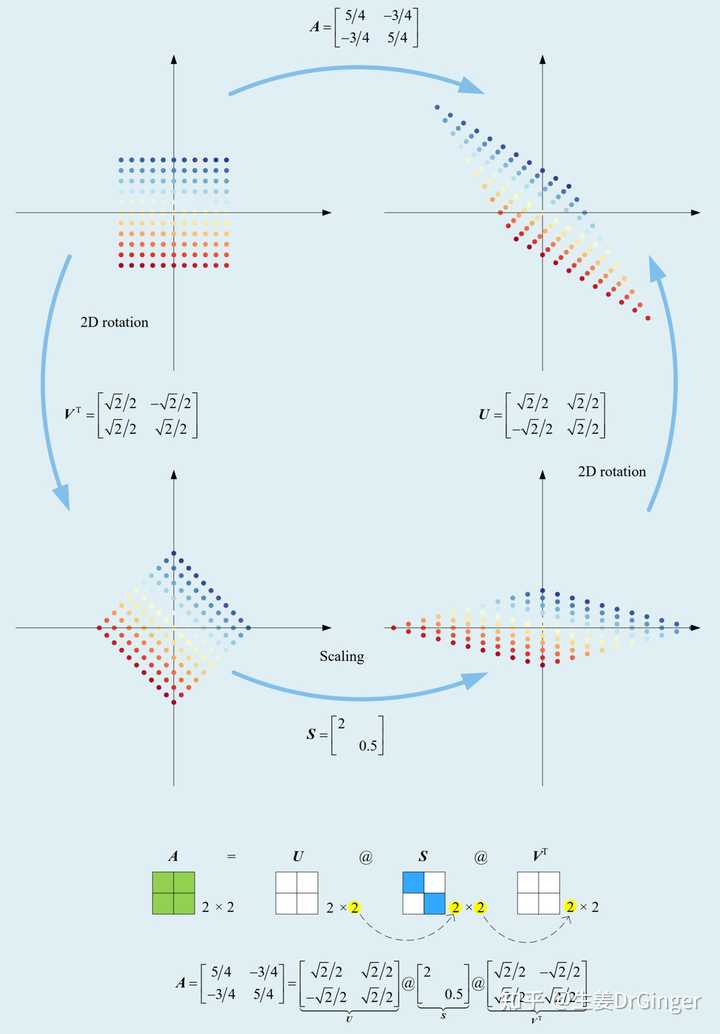
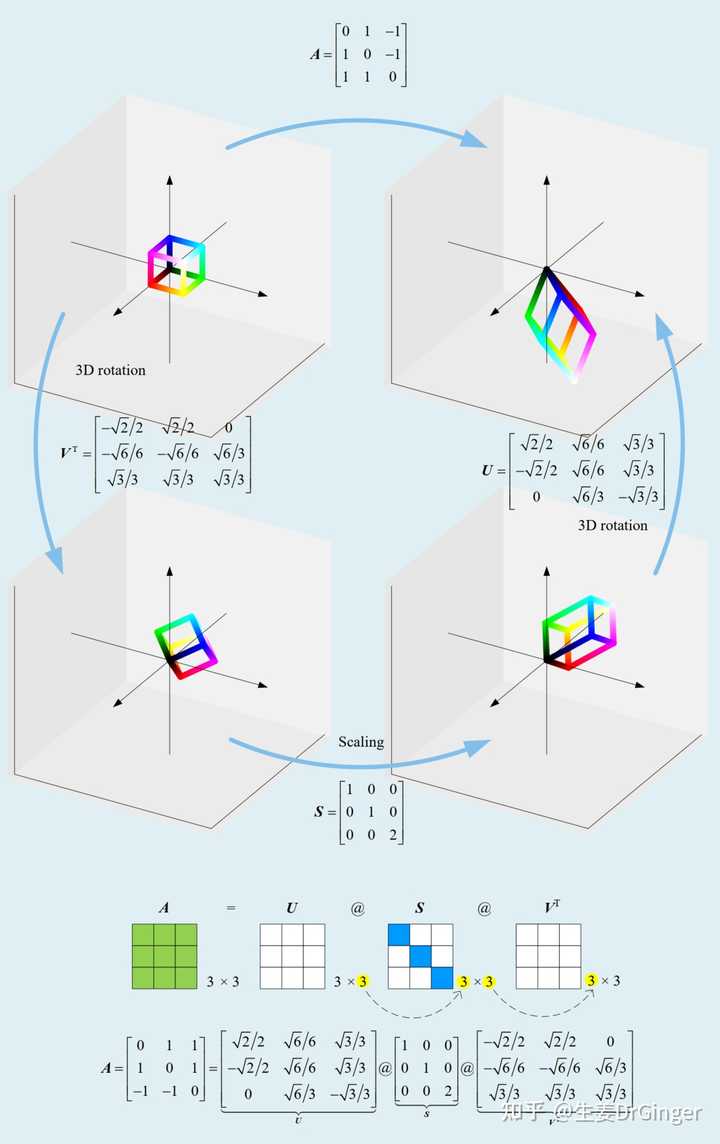
几何化，让你“看懂”奇异值分解 (Singular Value Decomposition)！用图形视角展示奇异值分解的几何直觉。

可视化奇异值分解， 2 × 2 方阵，第 1 组

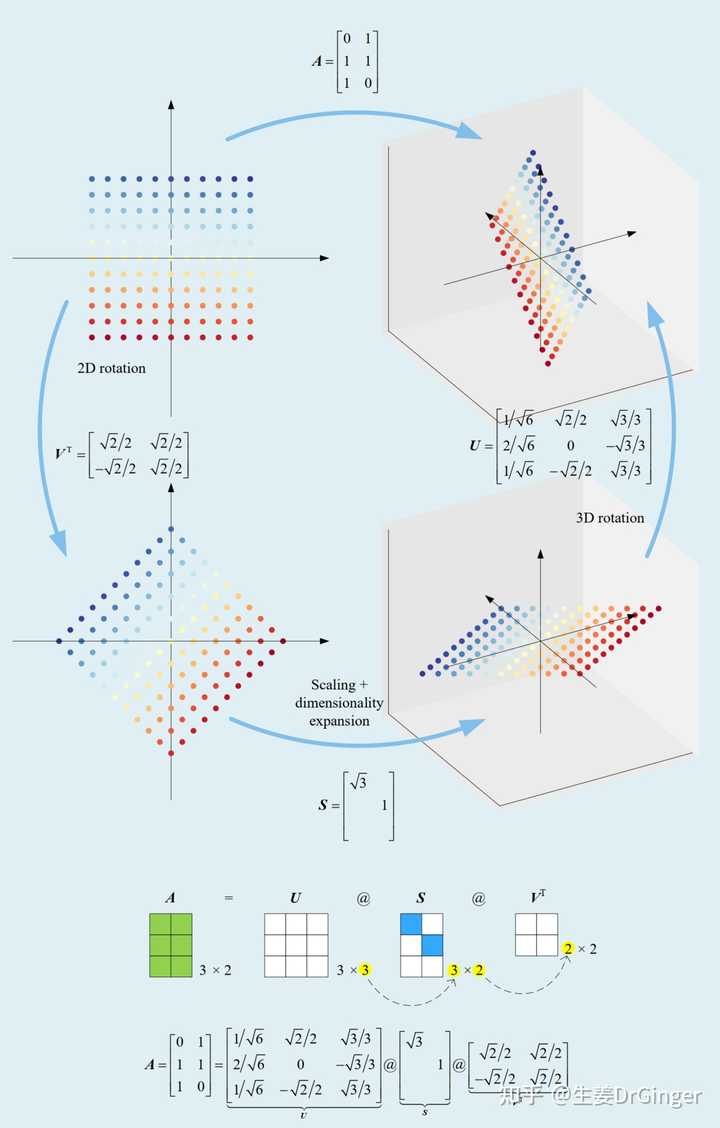
可视化奇异值分解， 3 × 3 方阵，第 1 组

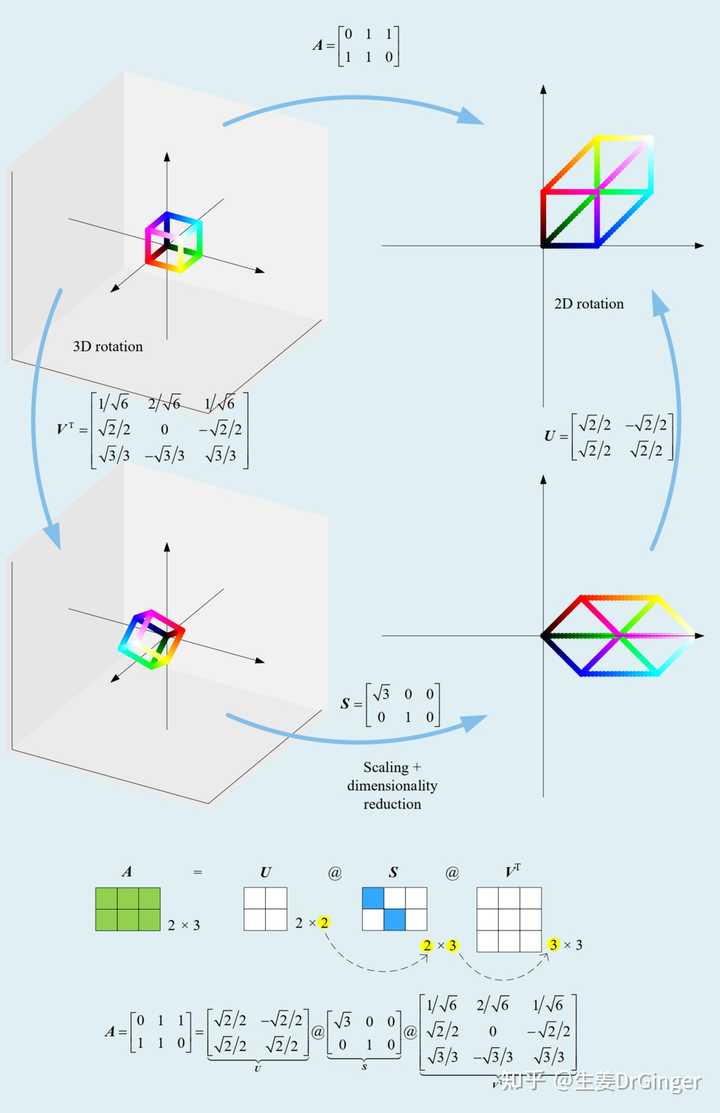
可视化奇异值分解，细高矩阵

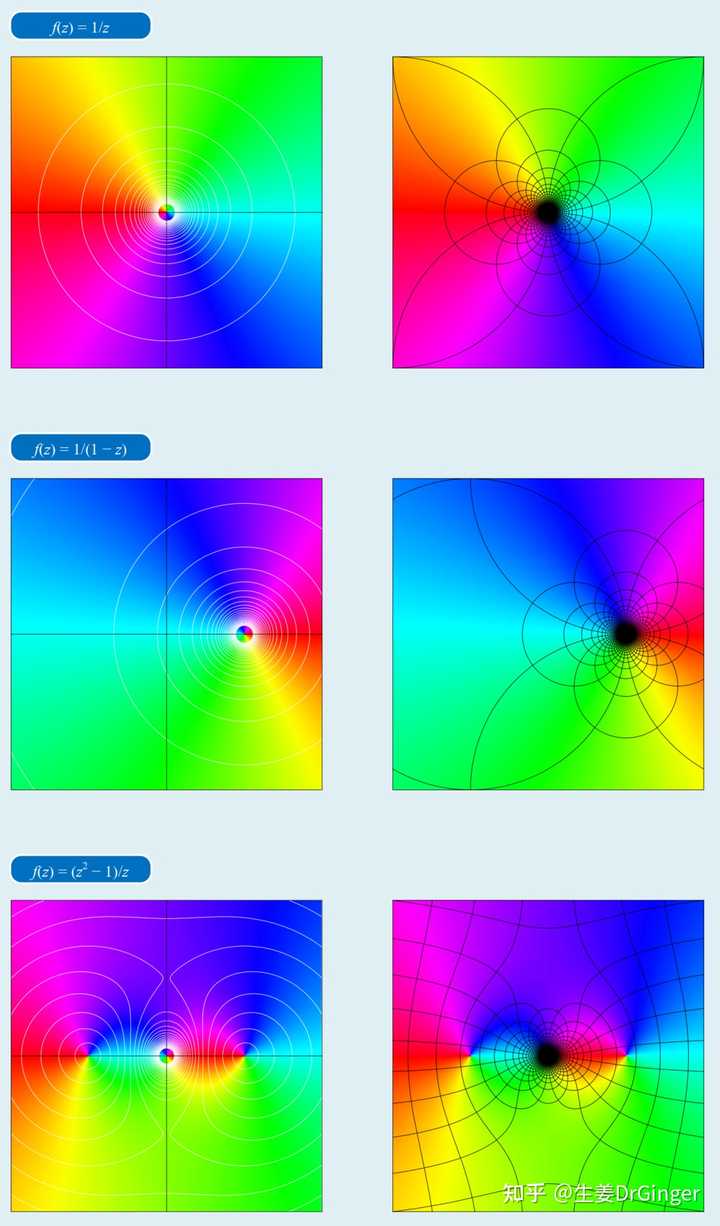
可视化奇异值分解，矮胖矩阵复变函数，丰富且美丽的线性、非线性变换。

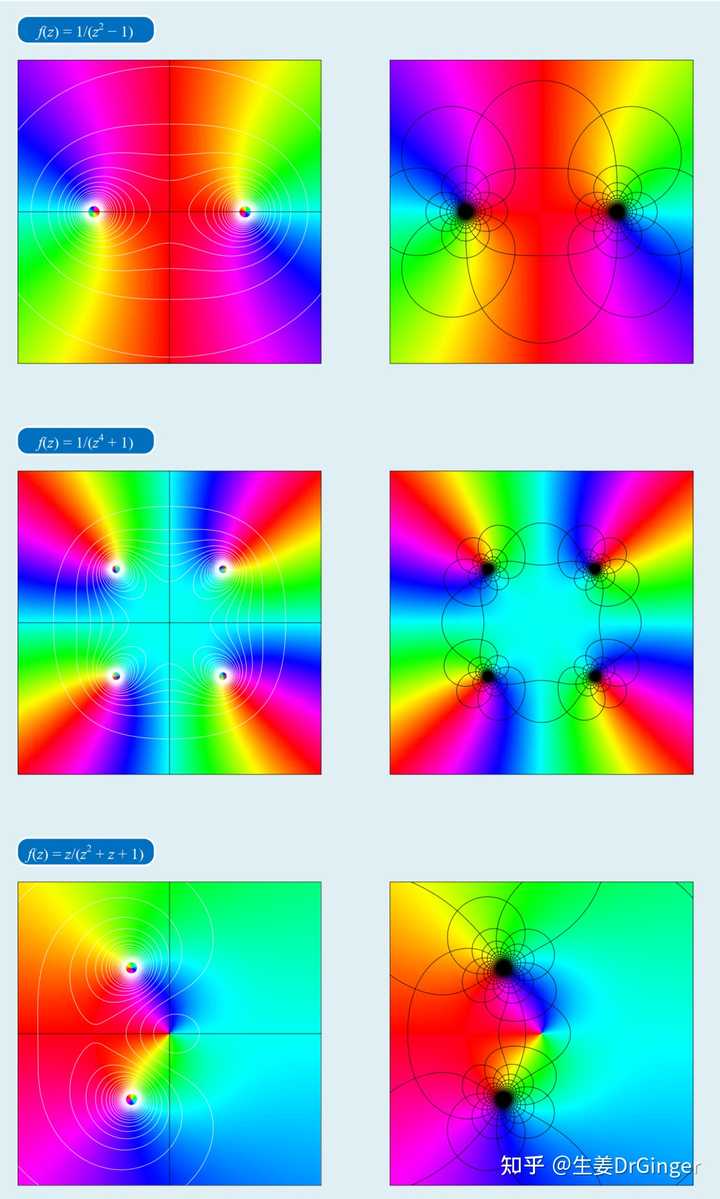
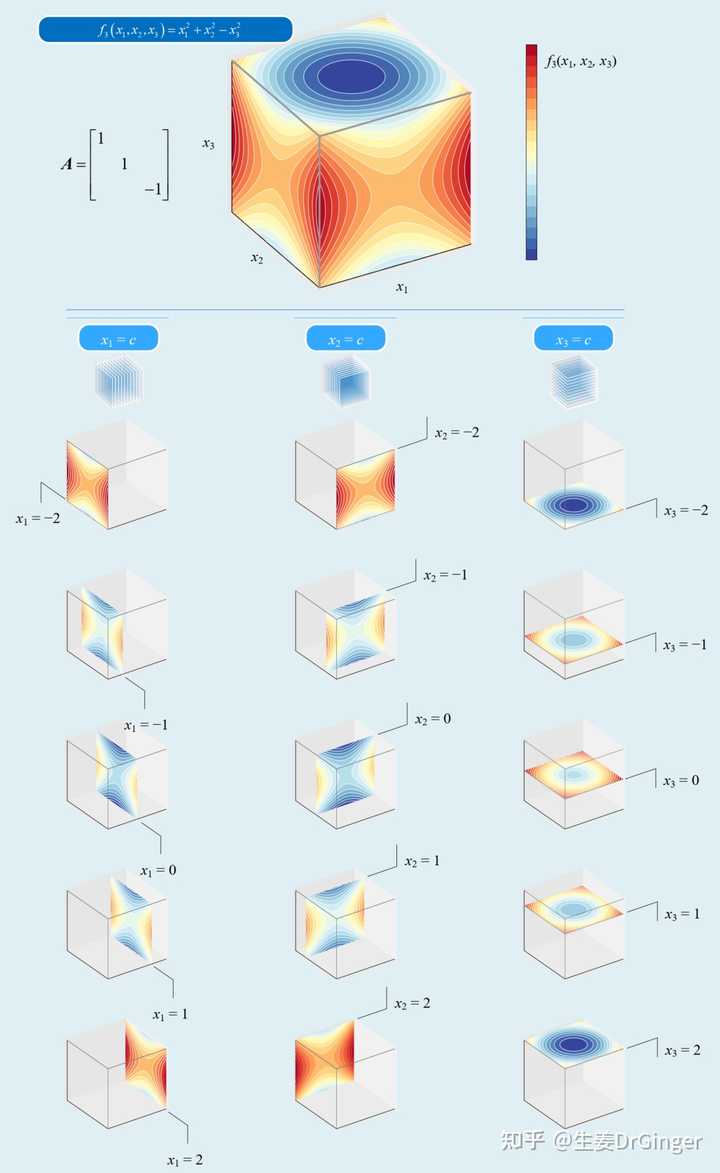
一元函数，线图；二元函数，三维网格面；三元函数，怎么可视化？？

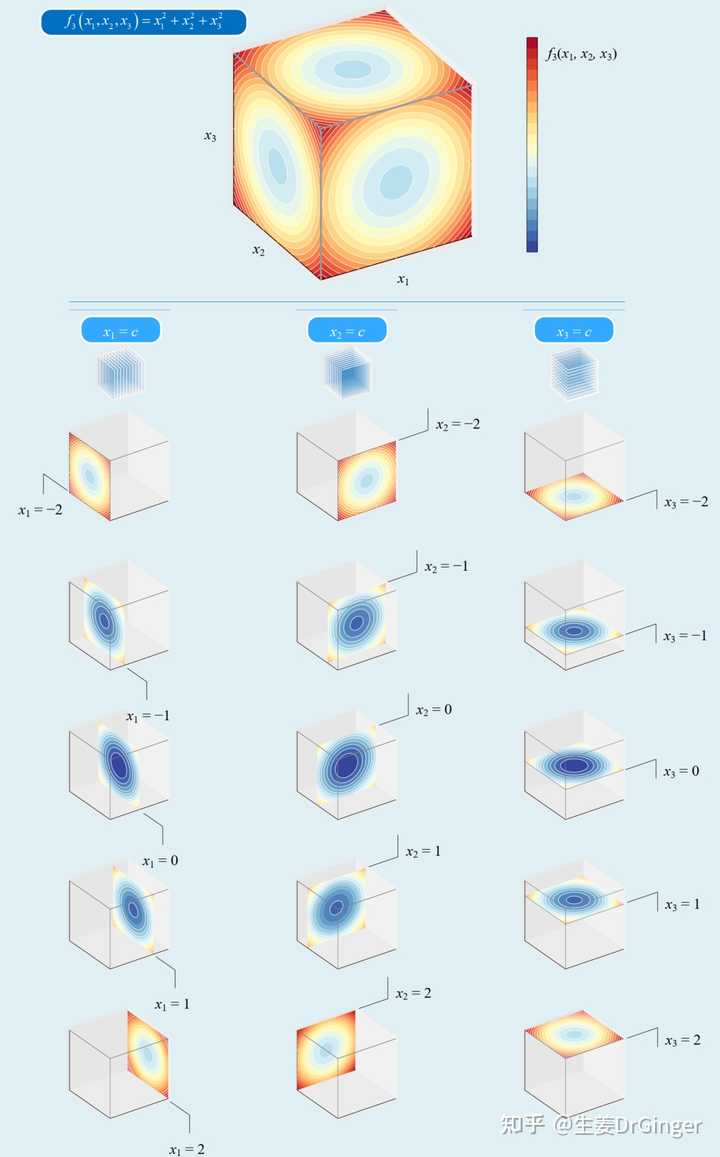
瑞利商 (Rayleigh quotient)，天生丽质难自弃！一个看似复杂线性代数概念，其实很美！

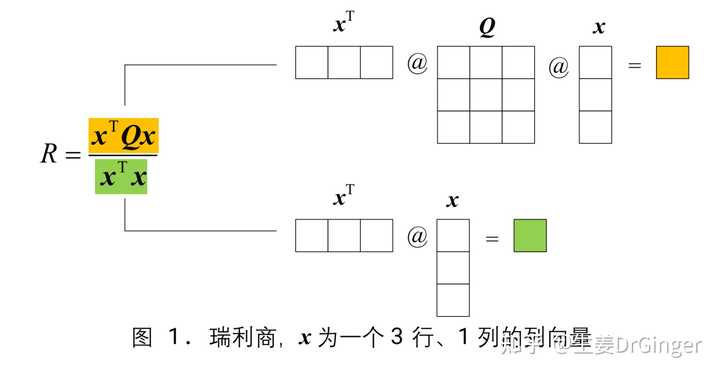
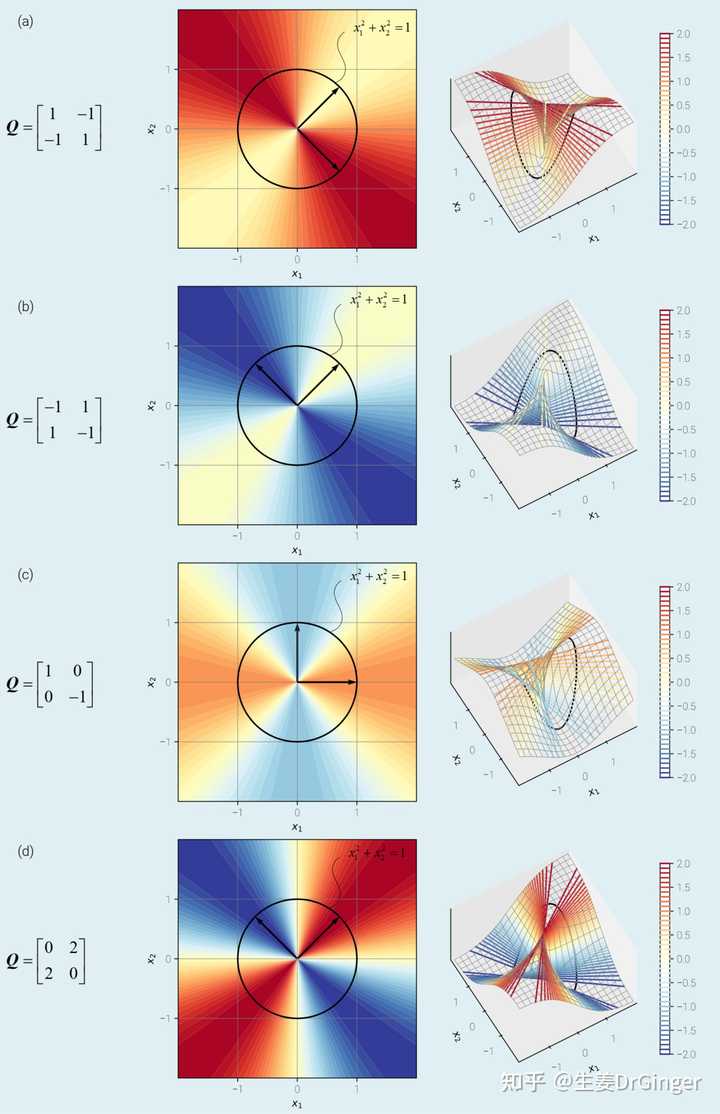
二元瑞利商

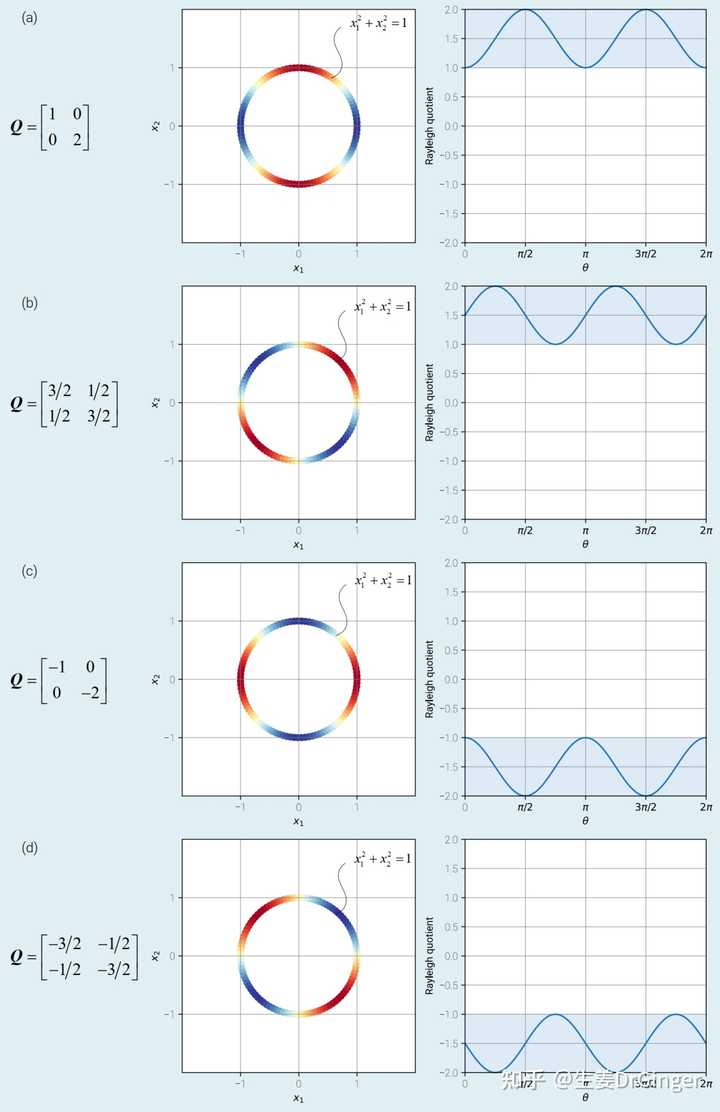
单位圆上看二元瑞利商

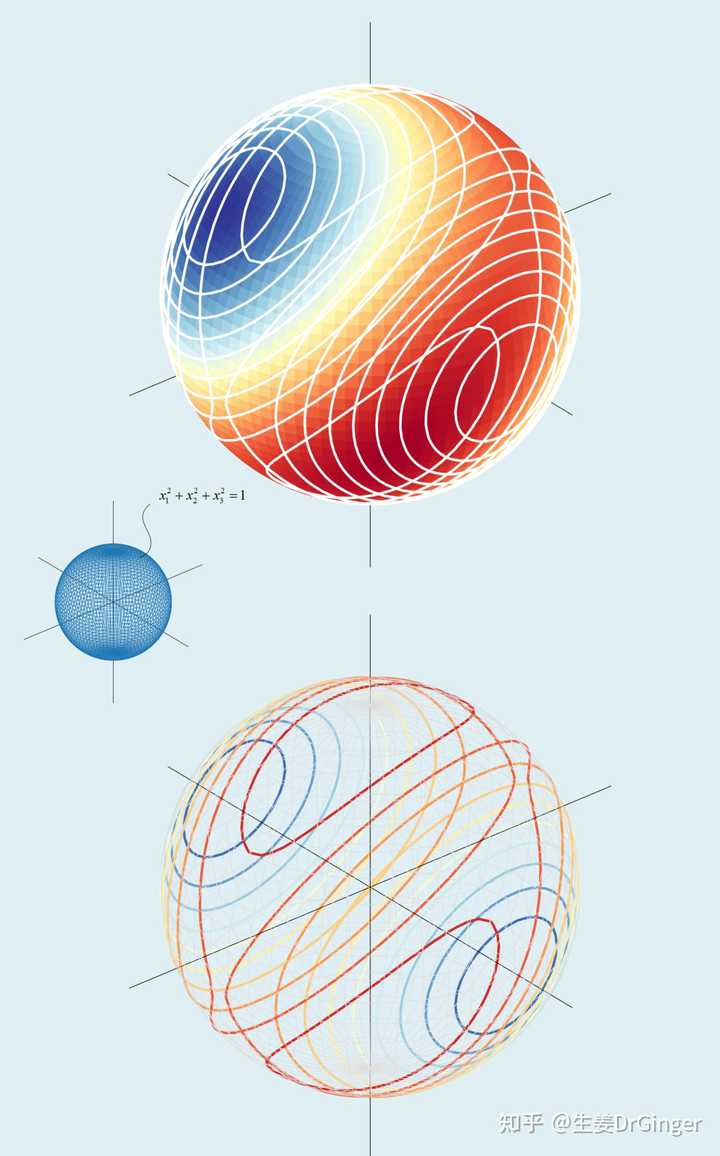
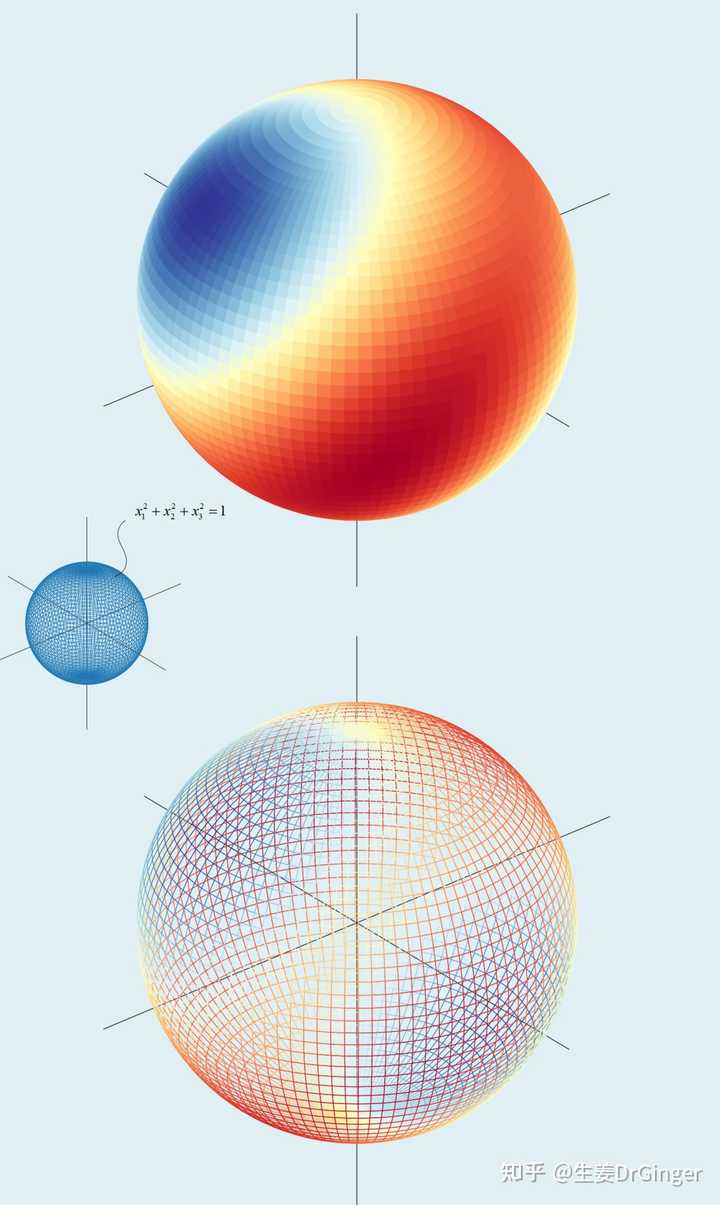
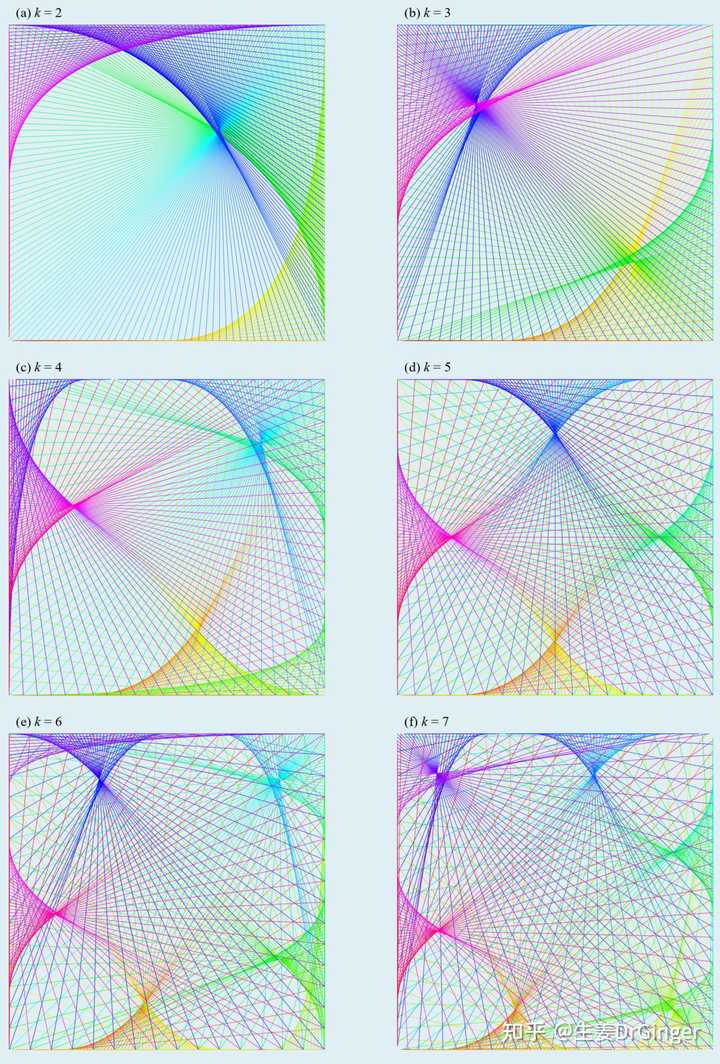
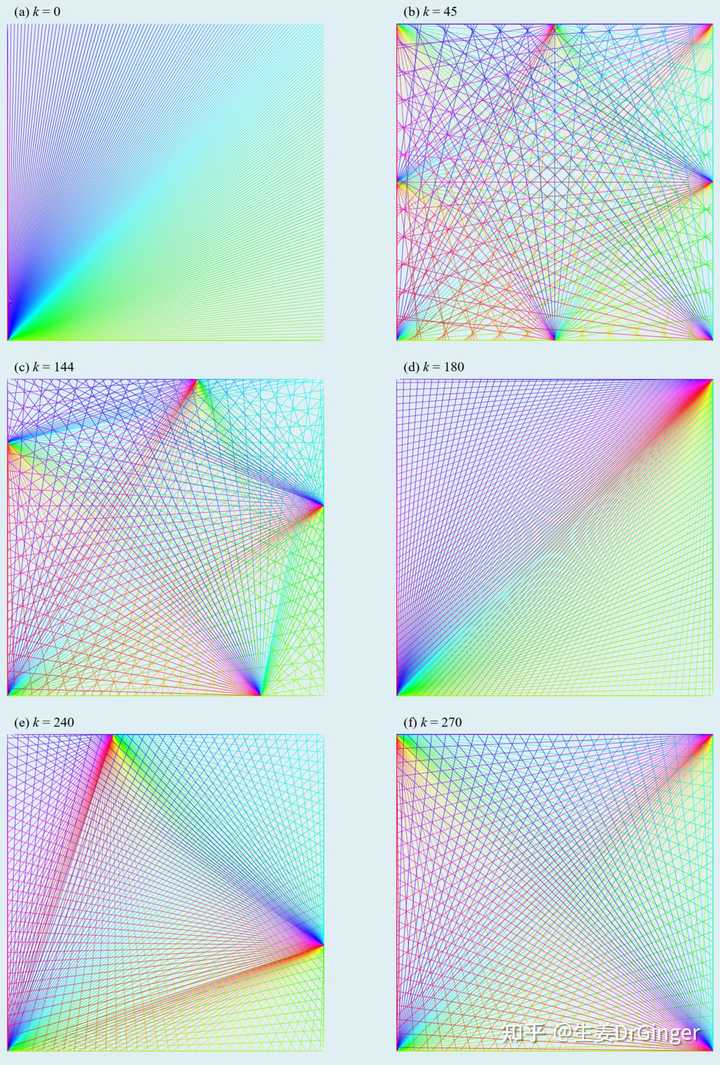
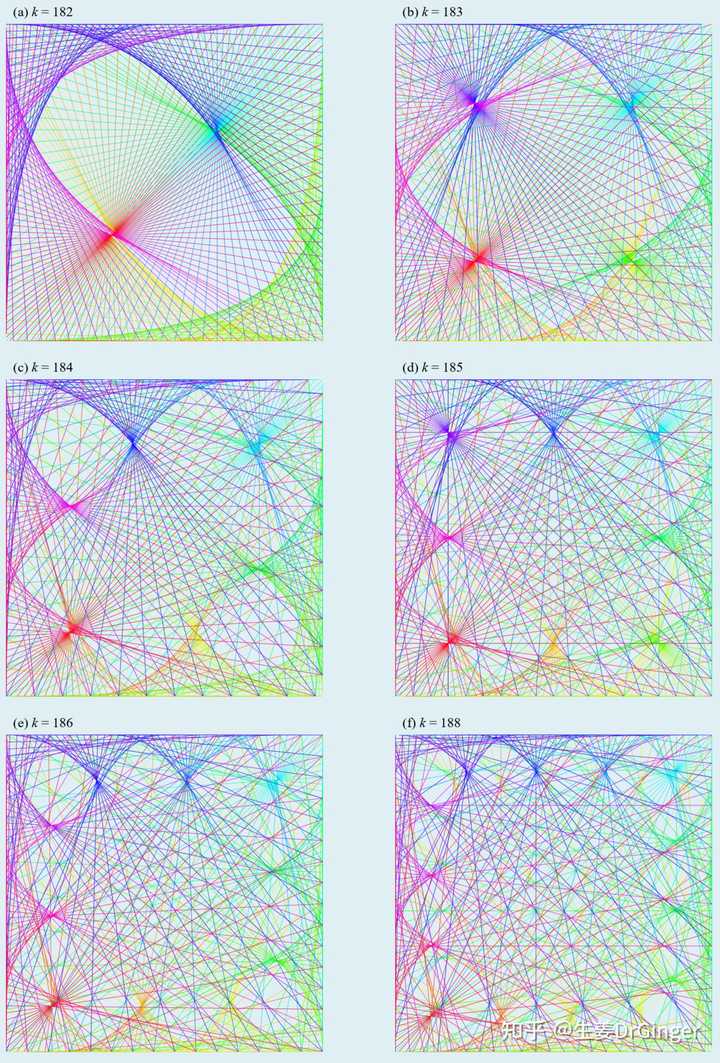
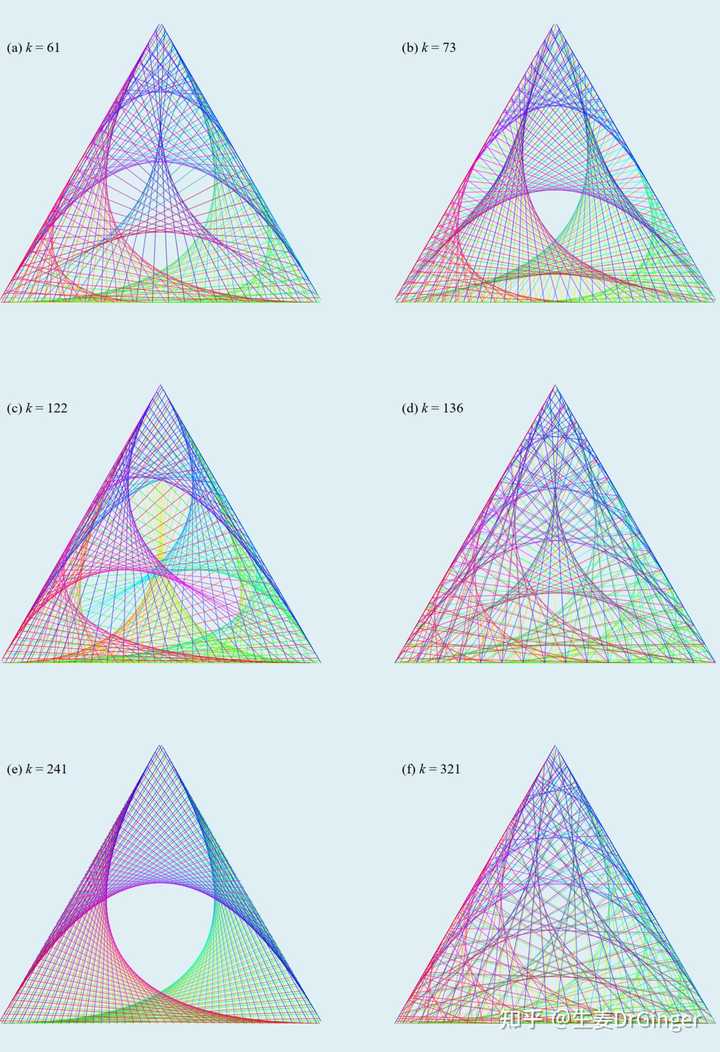
单位球面上的瑞利商模数乘法表的可视化！美的不要不要的！

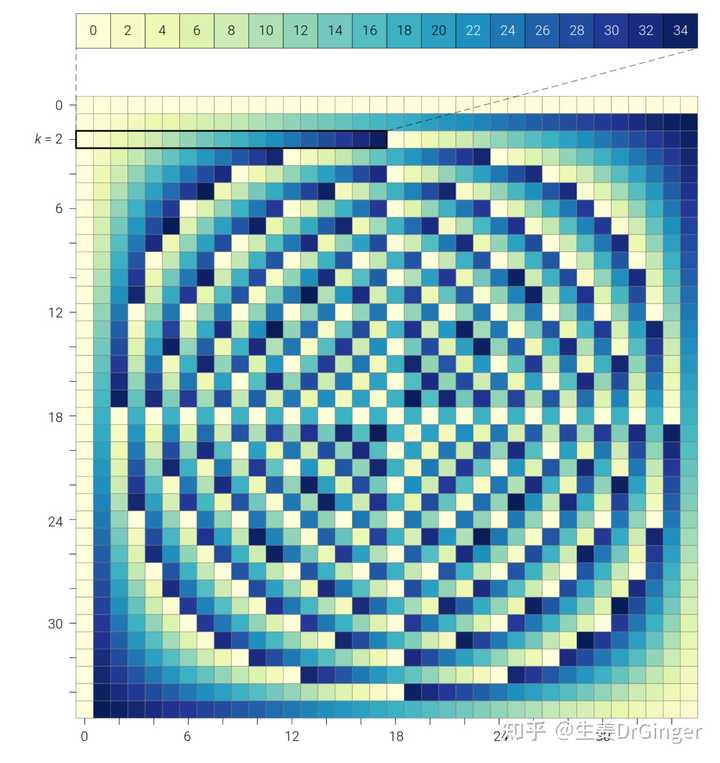
模数乘法表， mod 36

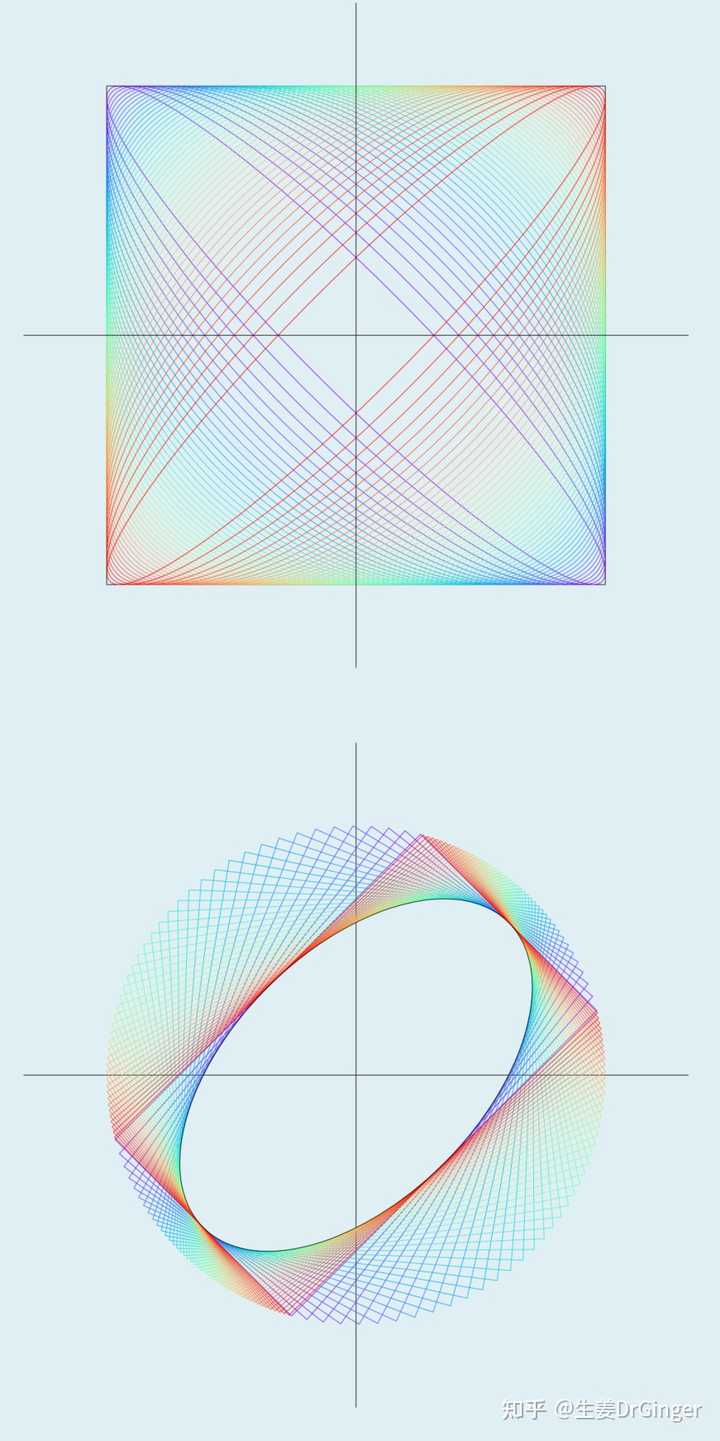
隐函数 (Implicit Functions)——等高线——提供绘制平面、立体几何形状的新思路

利用等高线绘制圆锥曲线、椭圆切线

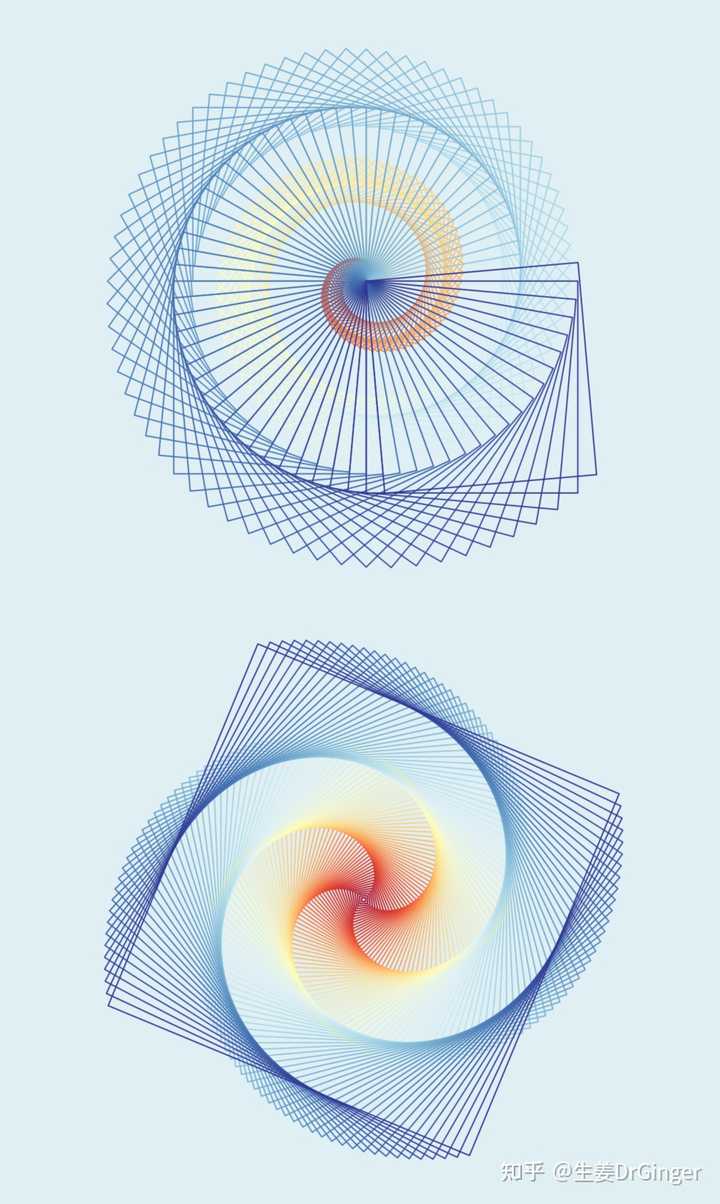
用等高线可视化隐函数曲面，第 1 组图形

等高线可视化范数。

三维等高线可视化范数。

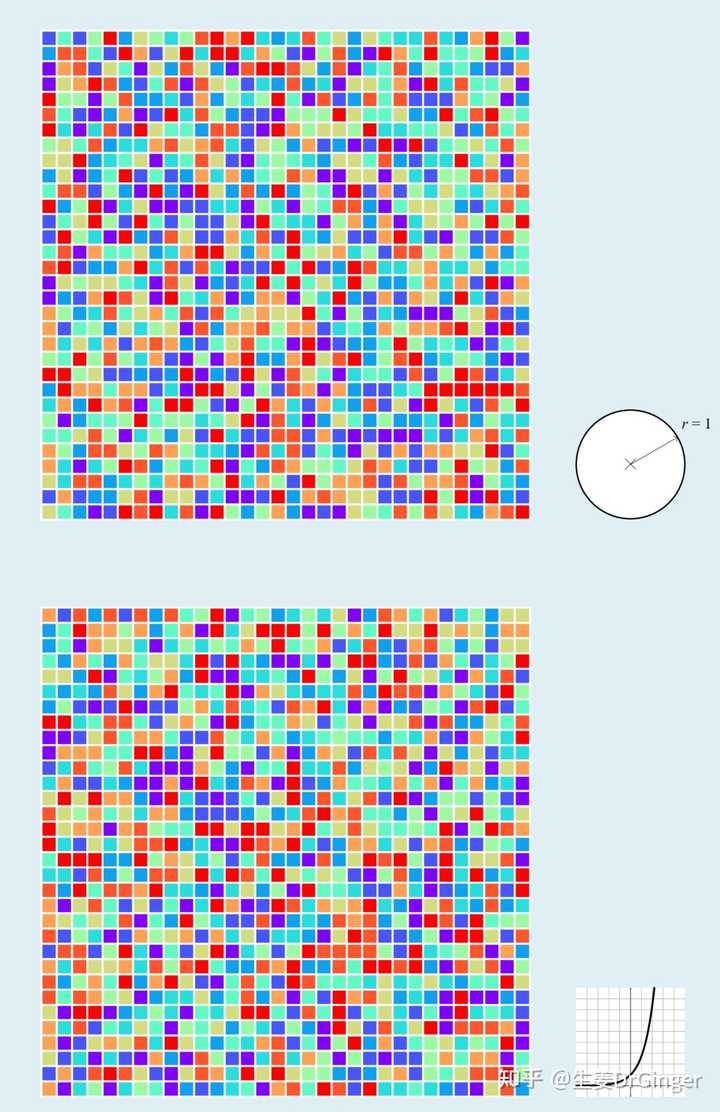
无限不循环小数做成热图，这个创意怎么样？！圆周率、根号2 ....

圆周率 π、自然对数底数 e，小数点后 1024 位热图

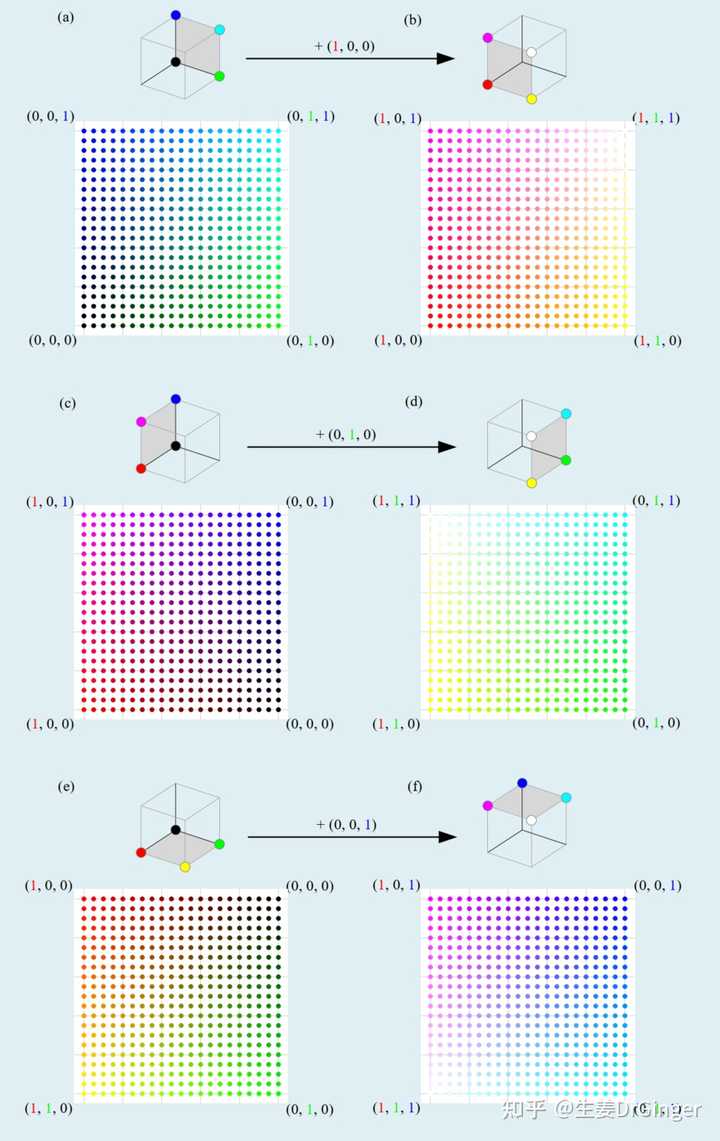
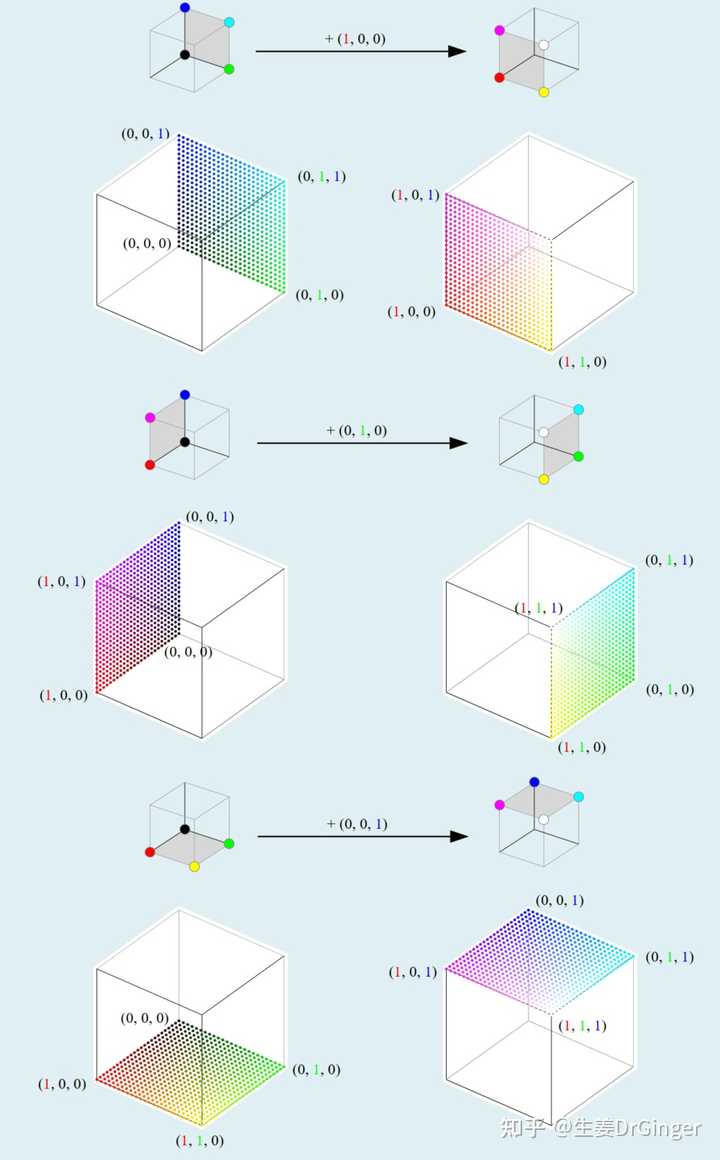
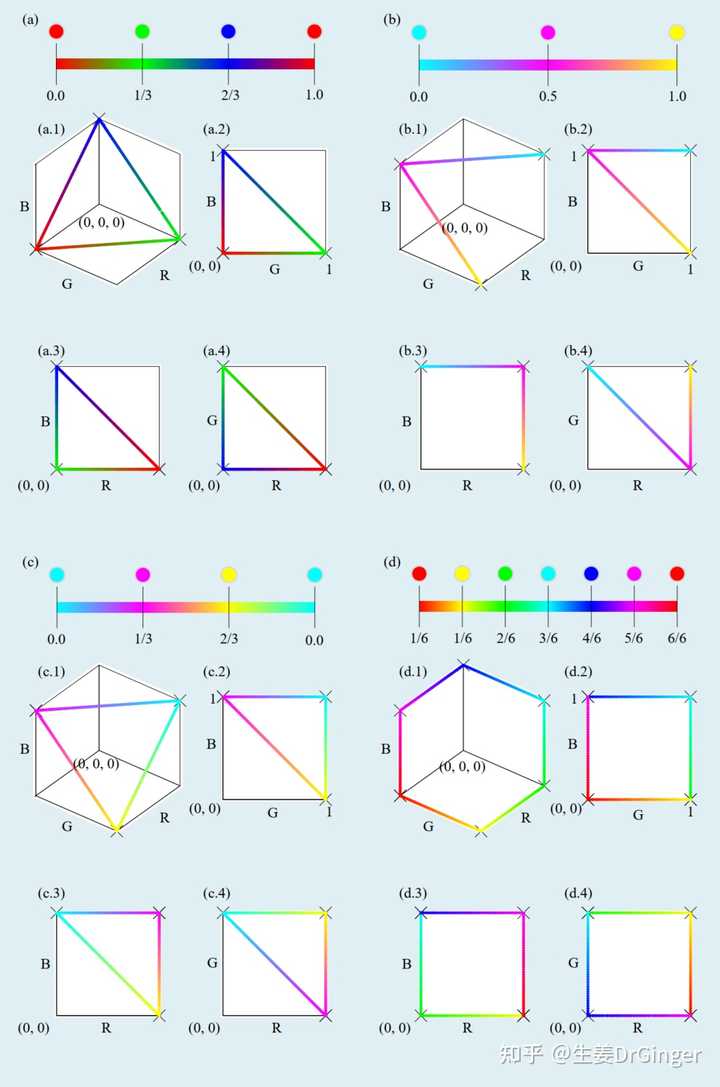
根号 2、黄金分割比，小数点后 1024 位热图
把RGB、CYMK色彩空间用几何的形式展示！

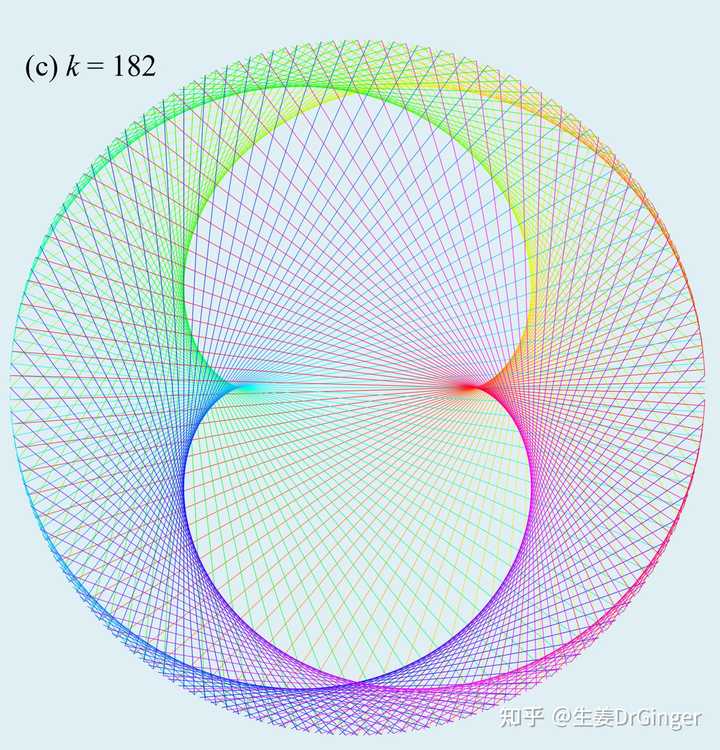
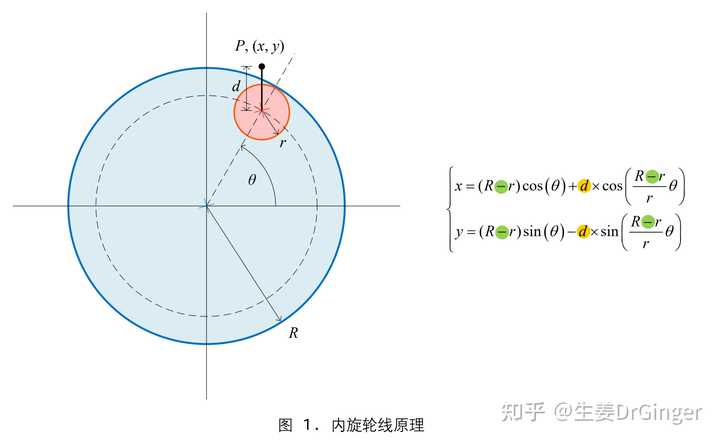
有没有想起小的时候玩得万花尺！繁花曲线 (Spirograph)，巧妙结合参数方程和物理学。

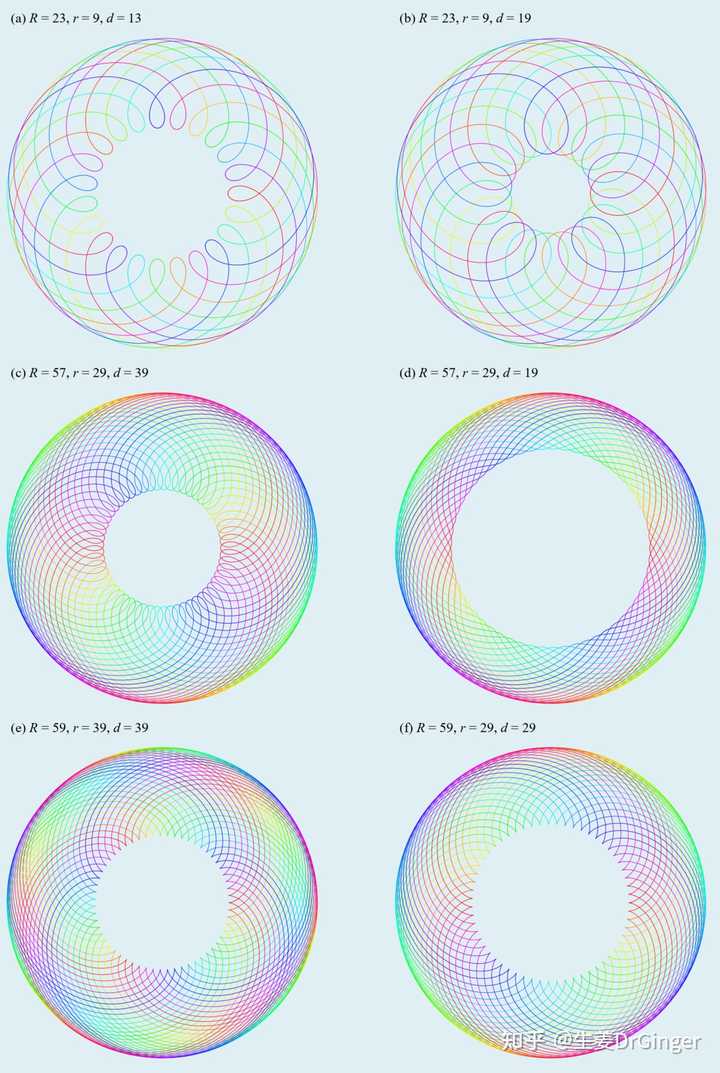
内旋轮线

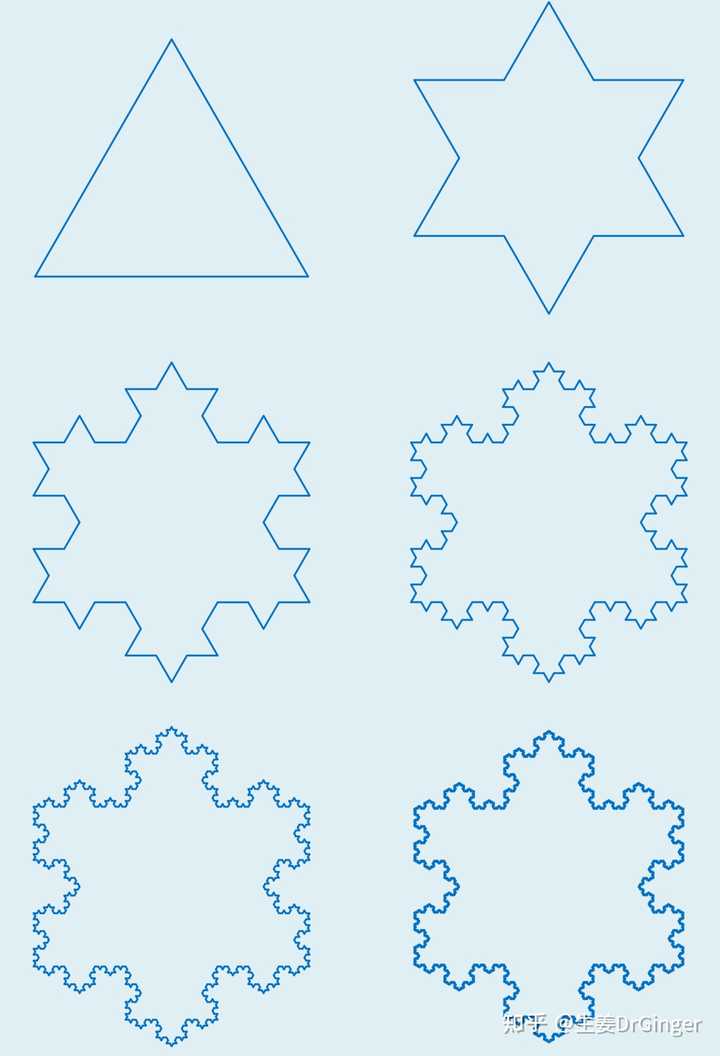
外旋轮线分形 (fractal)，自然界无处不在的自相似！

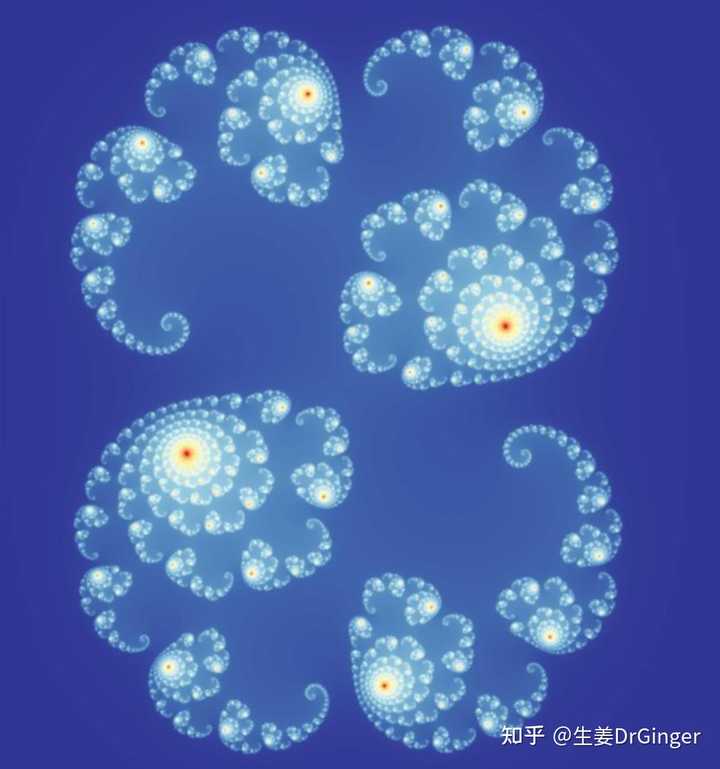
朱利亚集合，第 1 组

朱利亚集合，第 2 组

Koch 雪花

谢尔宾斯基三角形

勾股树

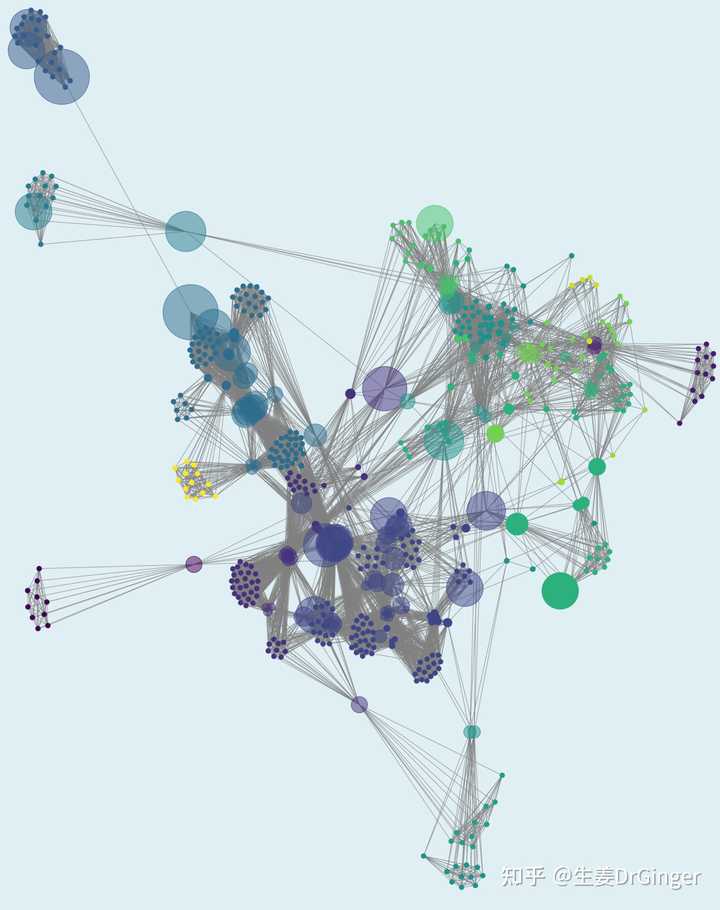
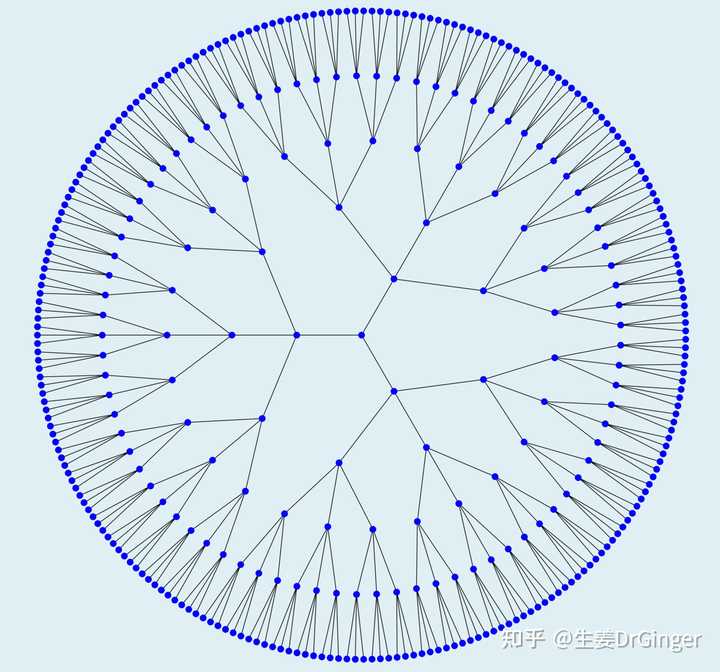
曼德博集合图论 (graph theory) 中的各种复杂结构肯定有一席！都挺美，有没有！

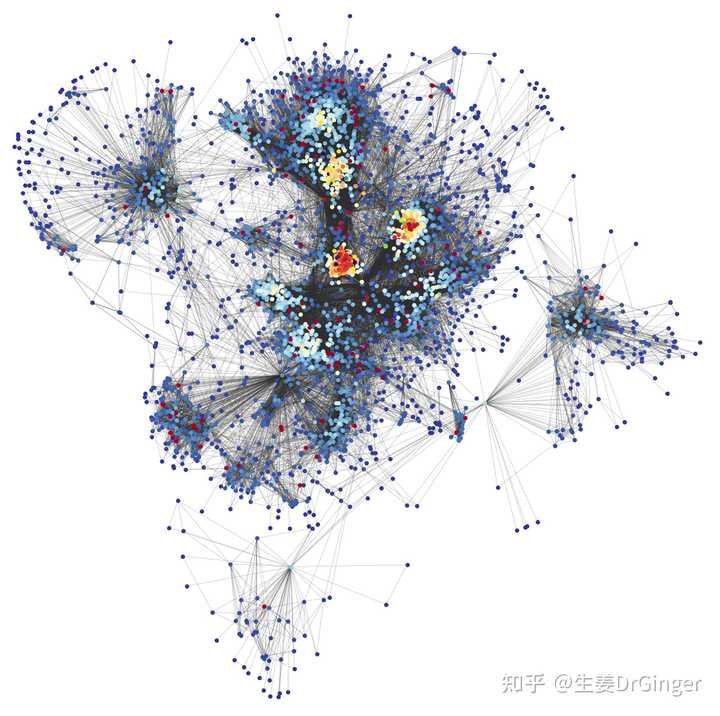
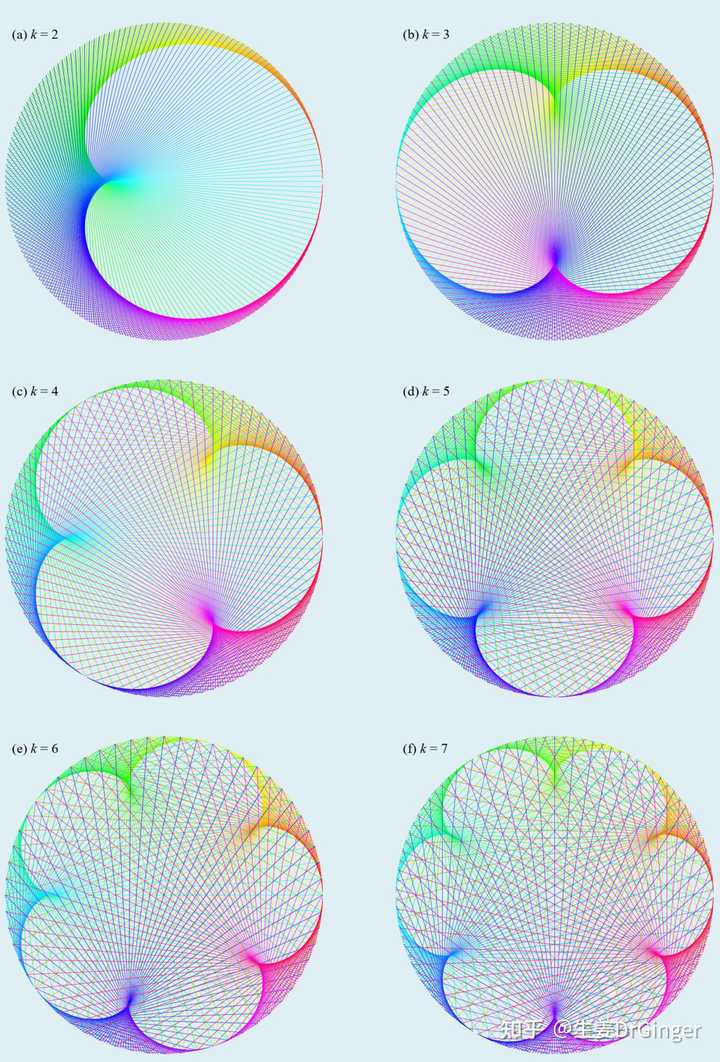
社交网络中节点的中心性心形线Cardioid，美出纸面！

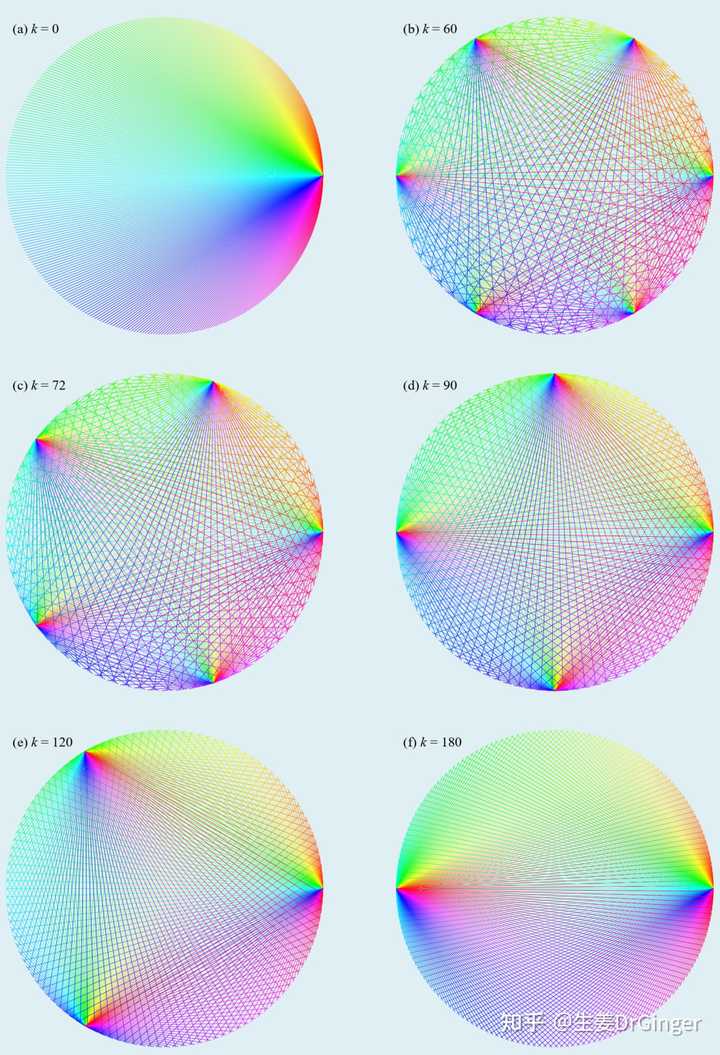
心形线的扩展图形，第 1 组

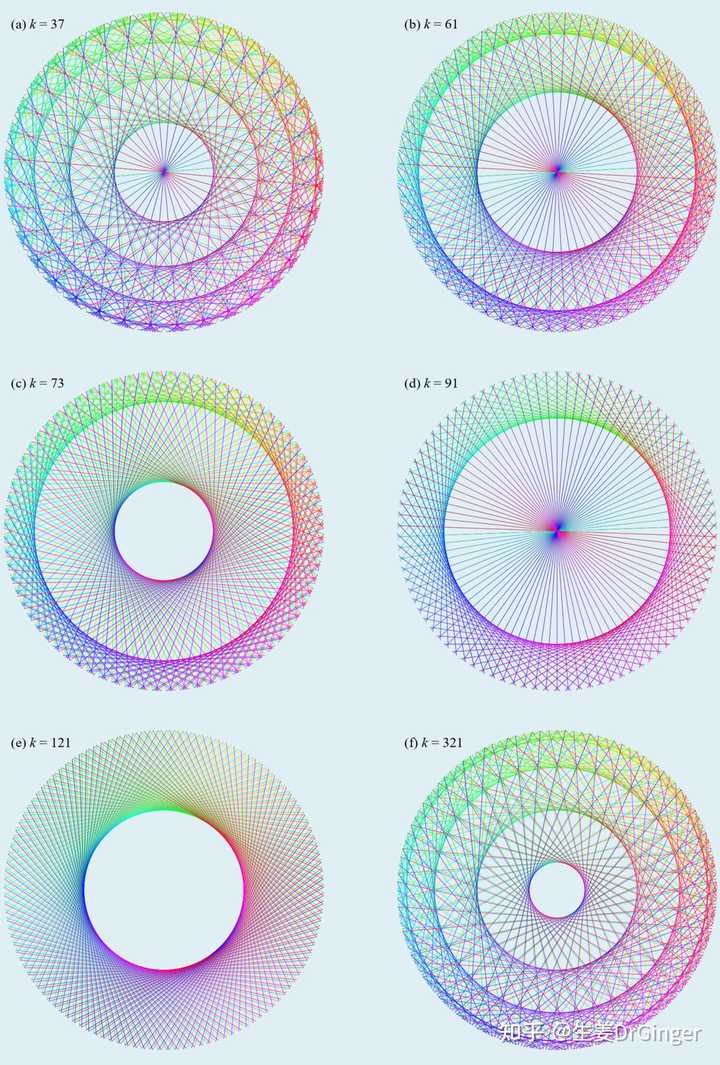
心形线的扩展图形，第 2 组

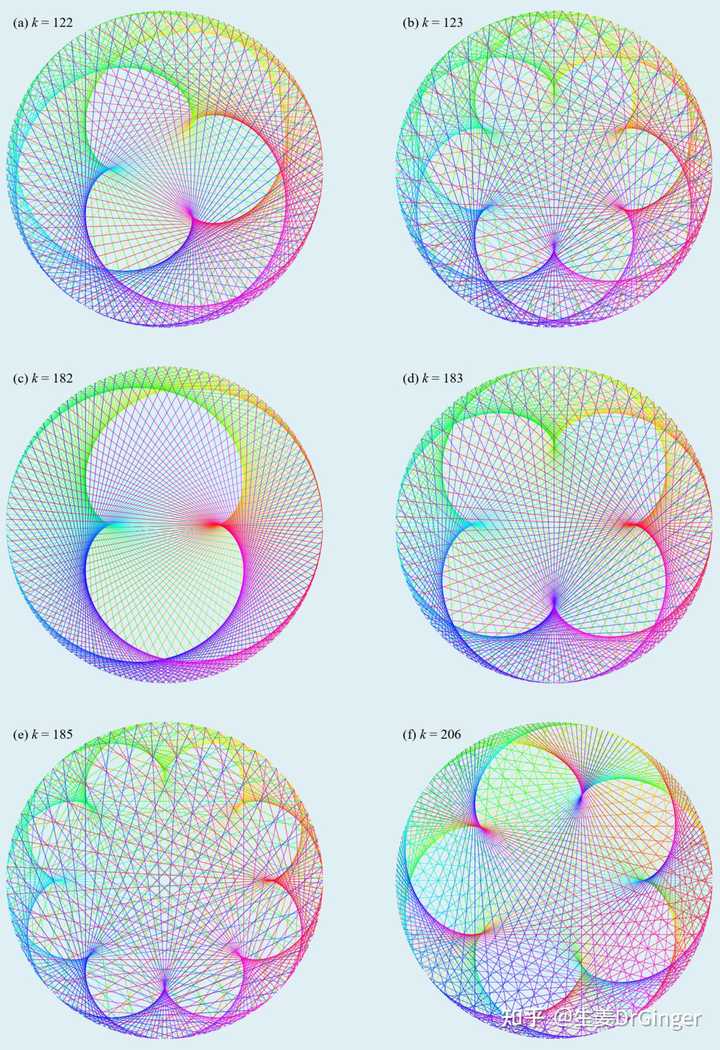
心形线的扩展图形，第 3 组

心形线的扩展图形，第 4 组

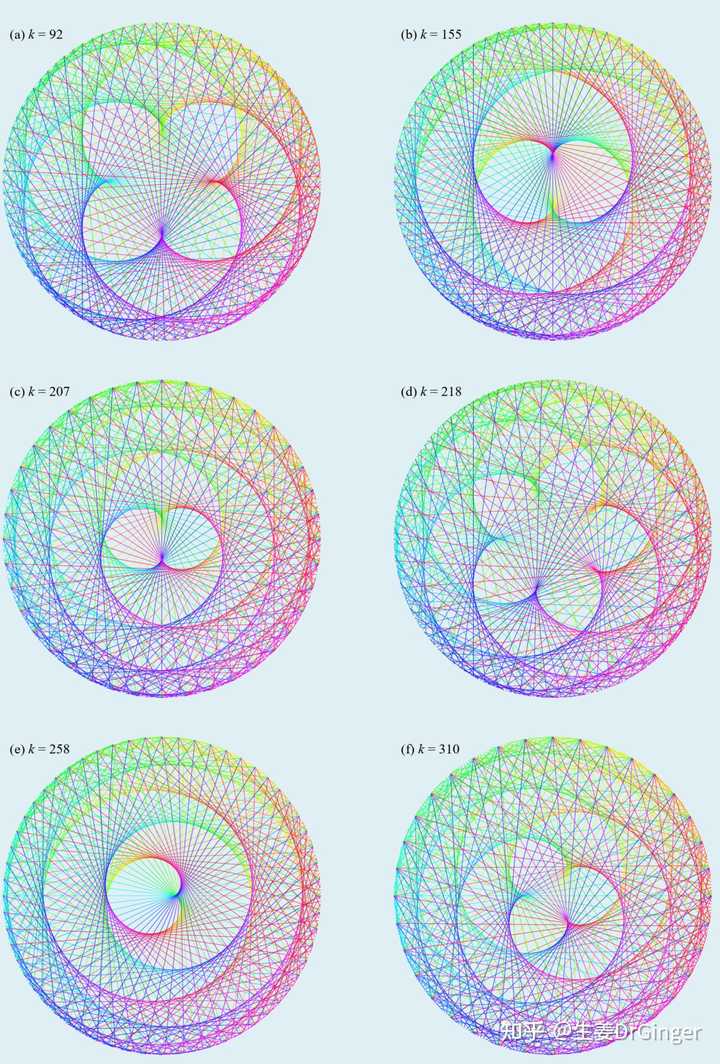
心形线的扩展图形，第 5 组

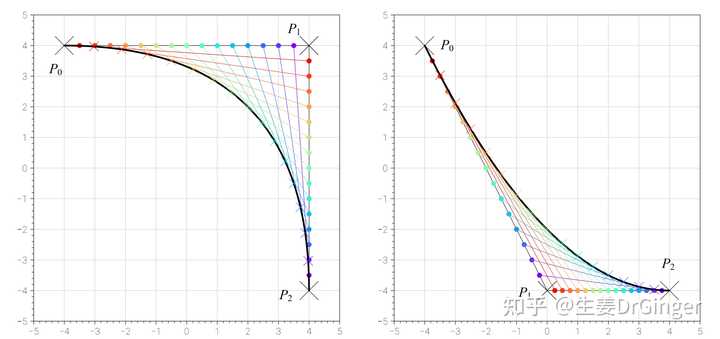
贝塞尔曲线 (Bézier Curve)，计算机图形学中特别重要的参数曲线！

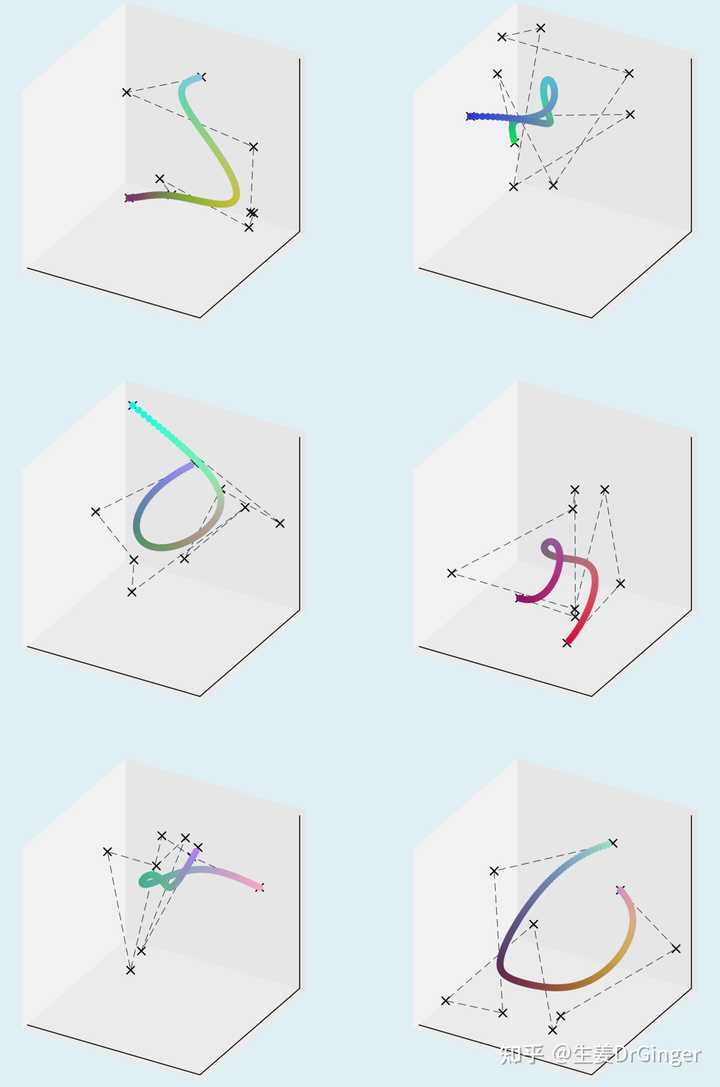
二阶贝塞尔曲线原理

RGB 色彩空间中的几个 8 阶贝塞尔曲线， 9 个控制点均由随机数发生器生成

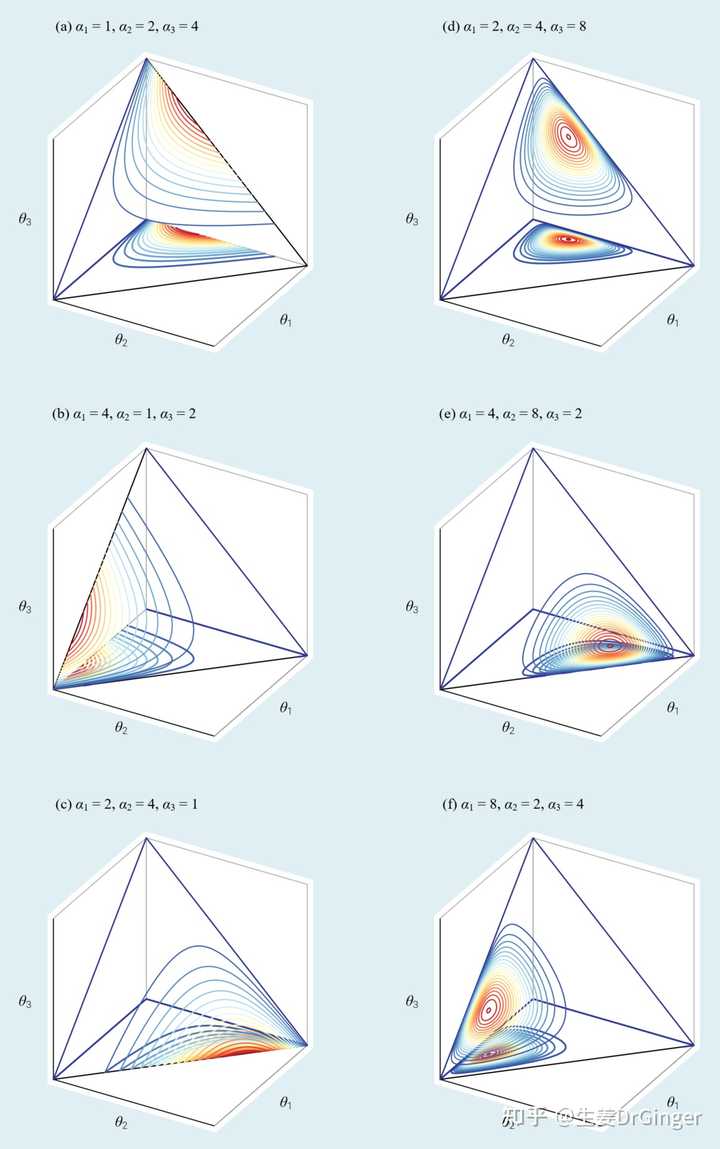
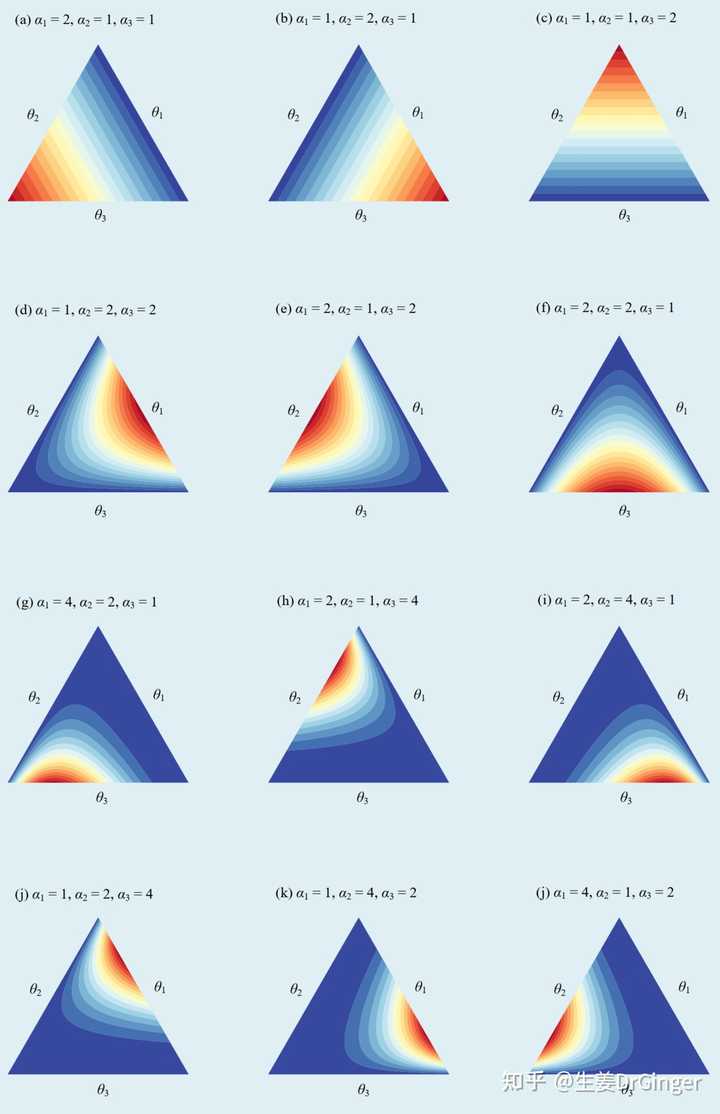
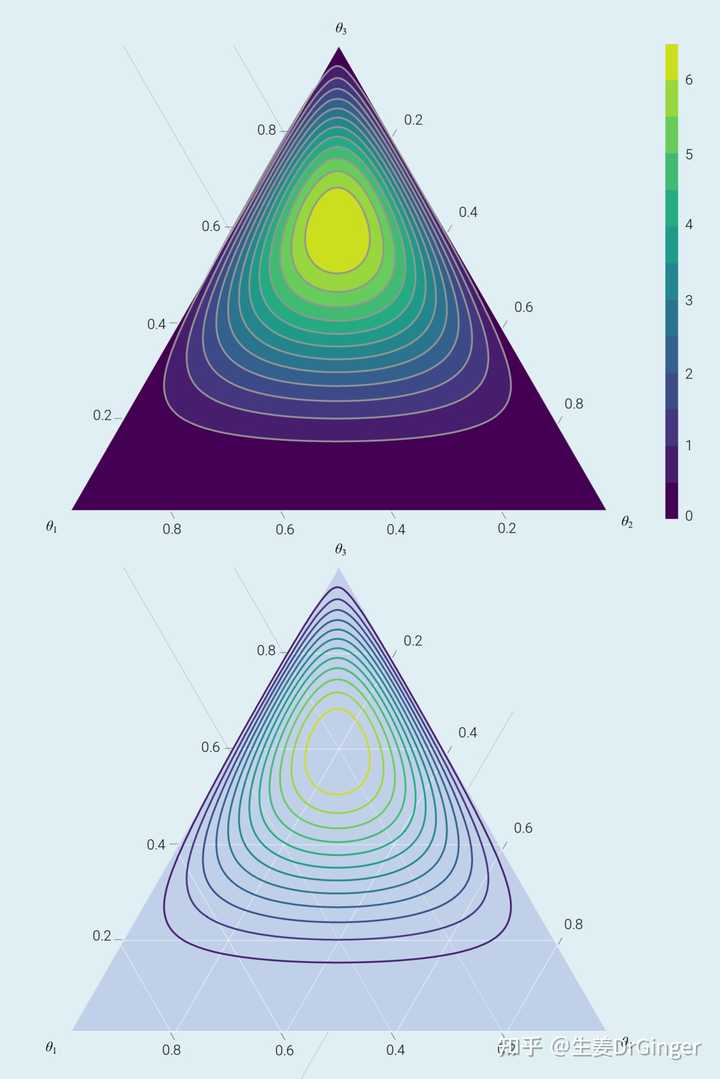
用贝塞尔曲线绘制的“鸢尾花曲线”Dirichlet分布，挺概率，挺几何，也挺美！用投影法、重心坐标系可视化 Dirichlet 分布！

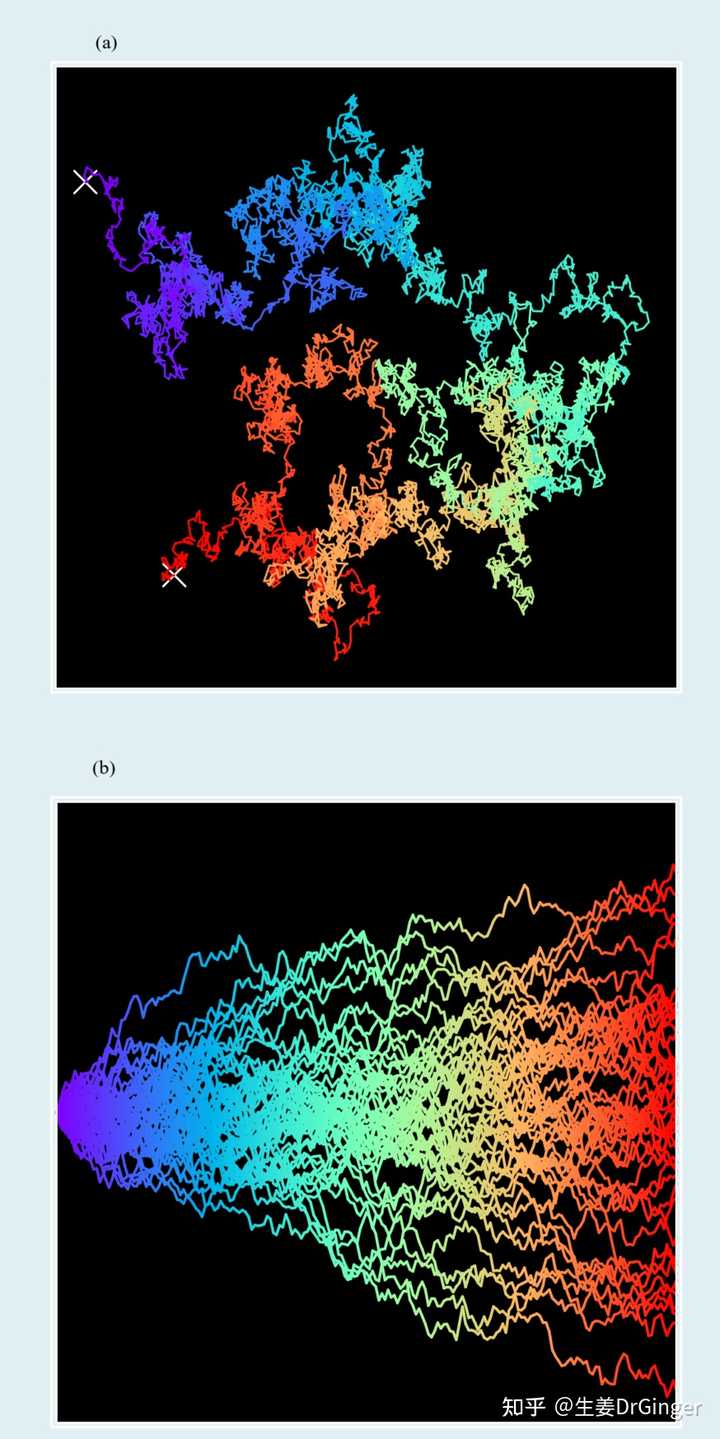
模式 + 随机：模式让世界充满秩序，随机让寰宇满是精彩！

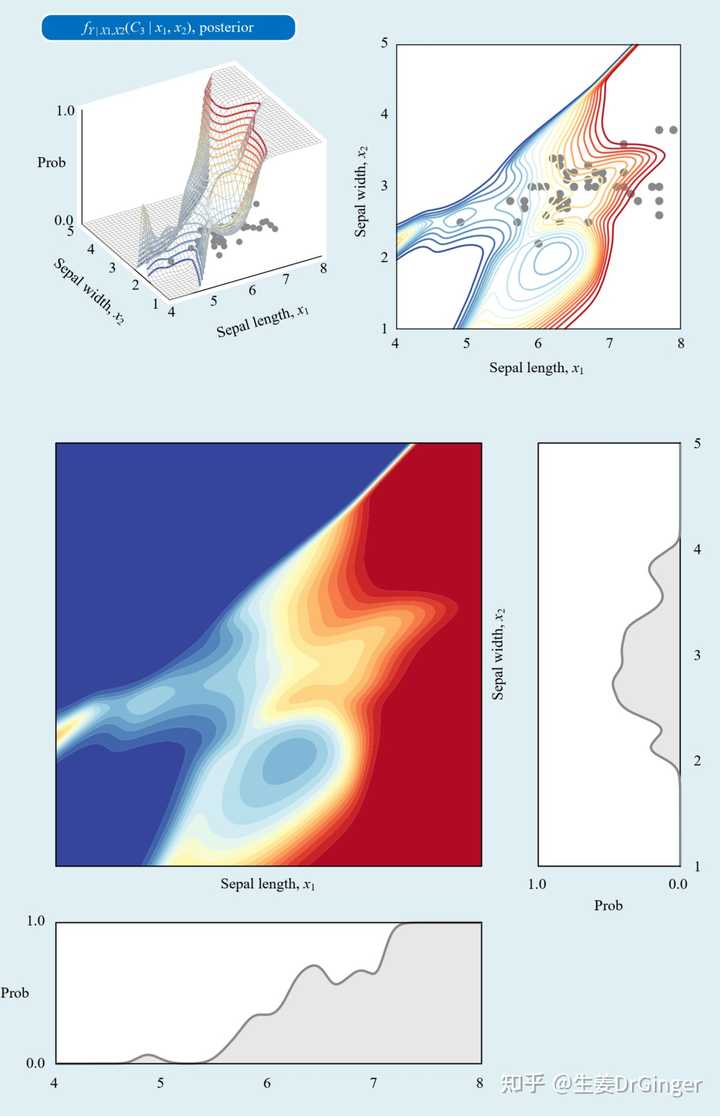
后验分布，这么可视化，成不成！？

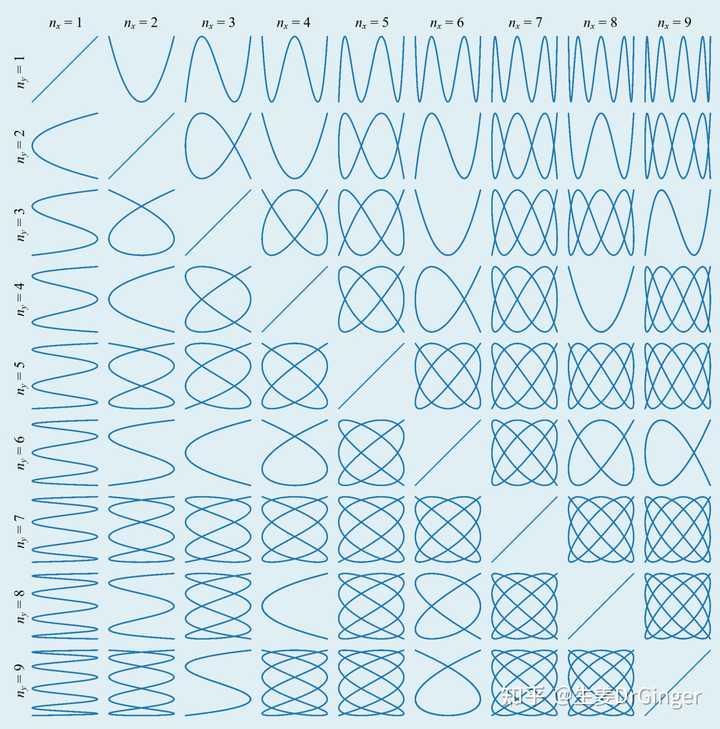
参数方程 (Parametric Equations)，又一种绘制平面、立体几何形状思路

利萨茹曲线， k = 0

利萨茹曲线， k = 2

利萨茹曲线， k 变化

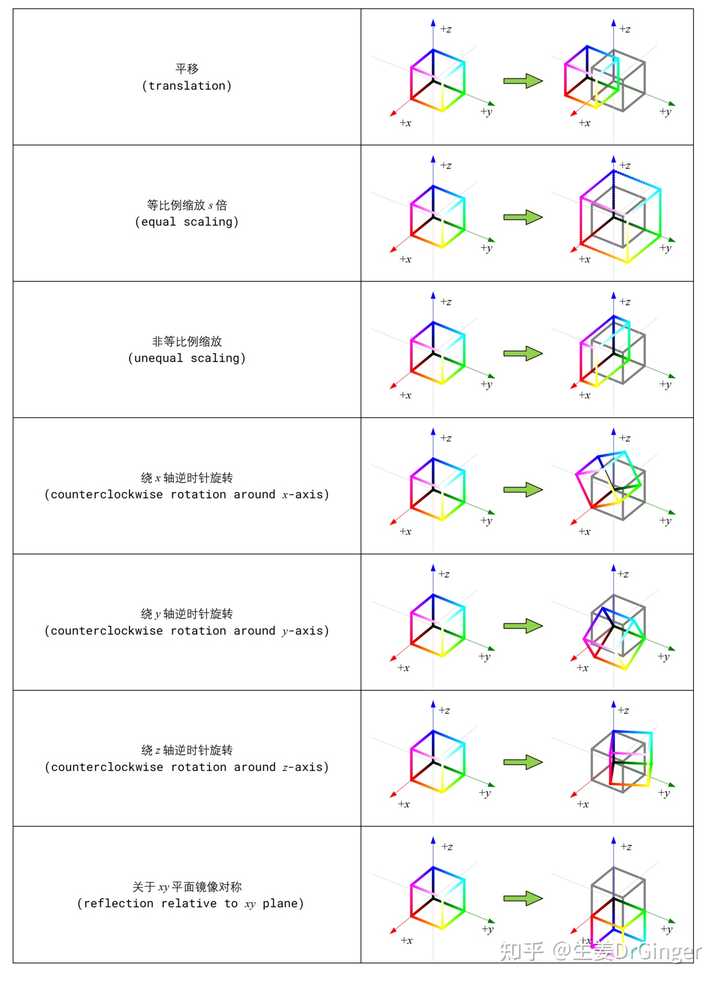
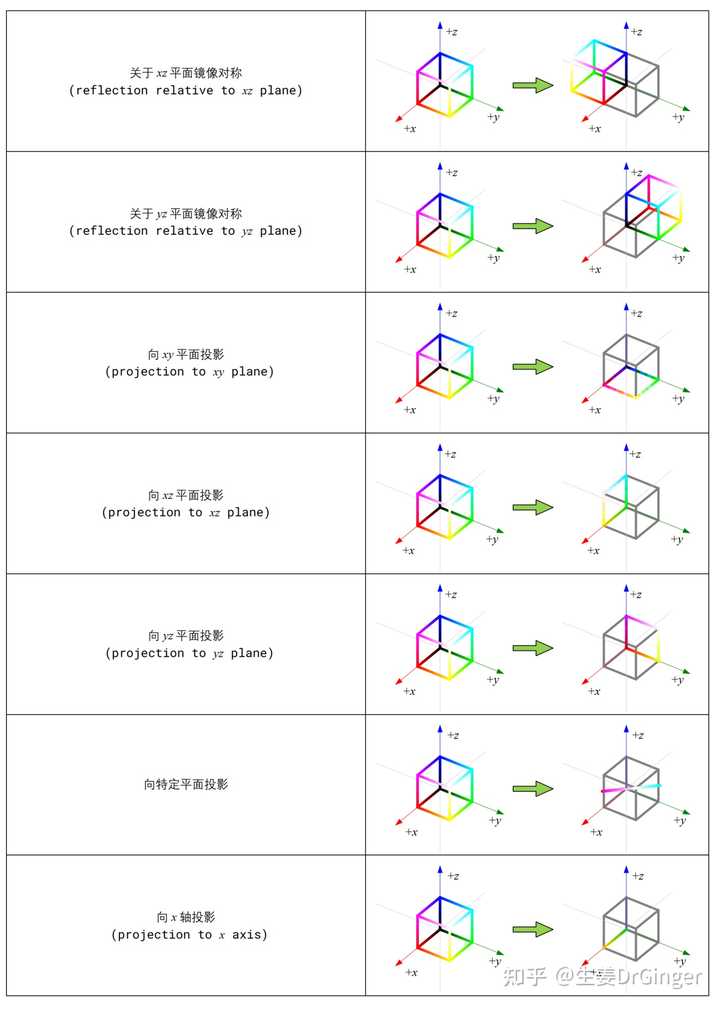
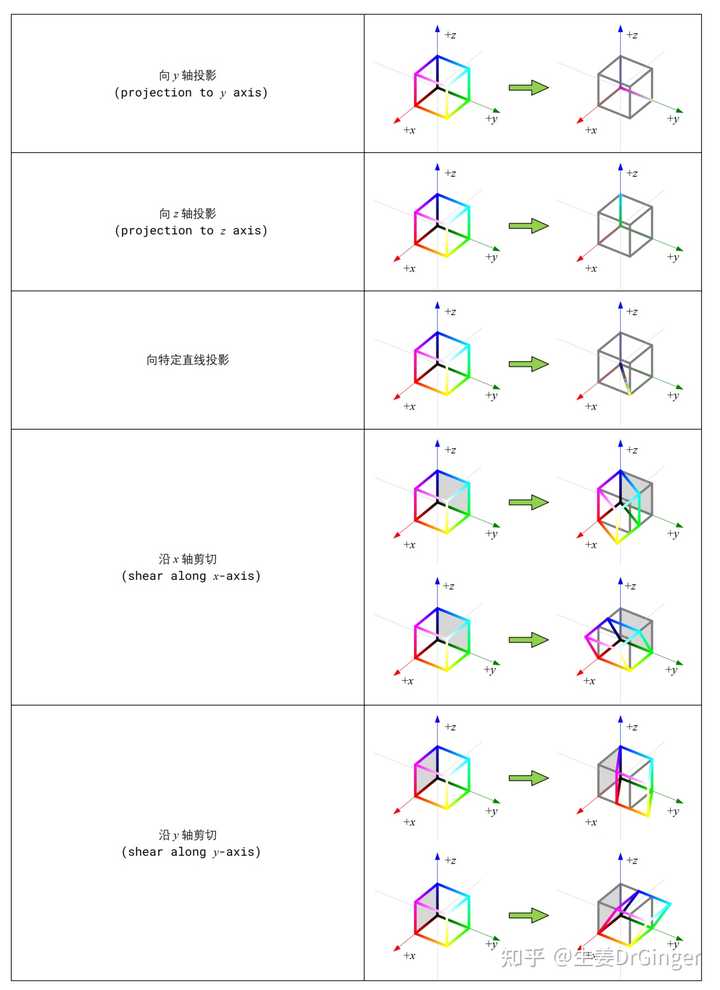
立体几何变换 (Geometric Transformations in 3D Space)，三维空间看平移、缩放、旋转、镜像、投影、剪切。

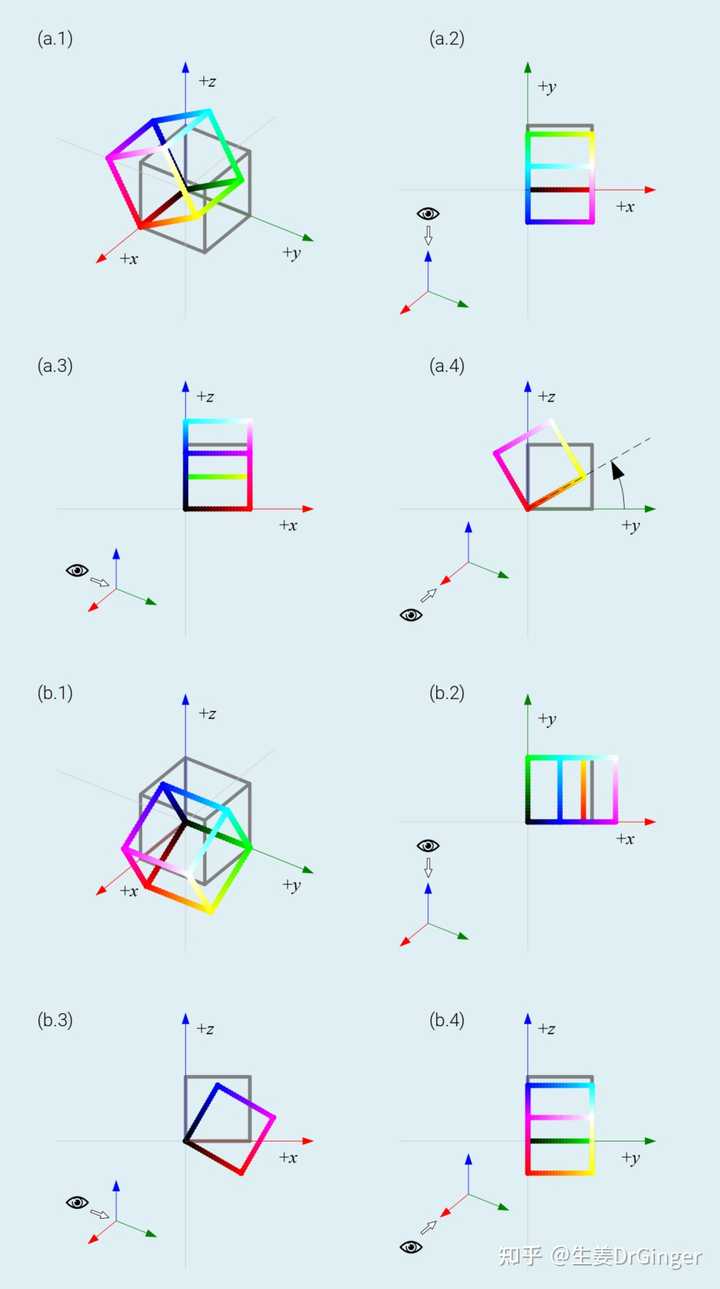
RGB 立方体框线： (a) 等比例缩放； (b) 非等比例缩放

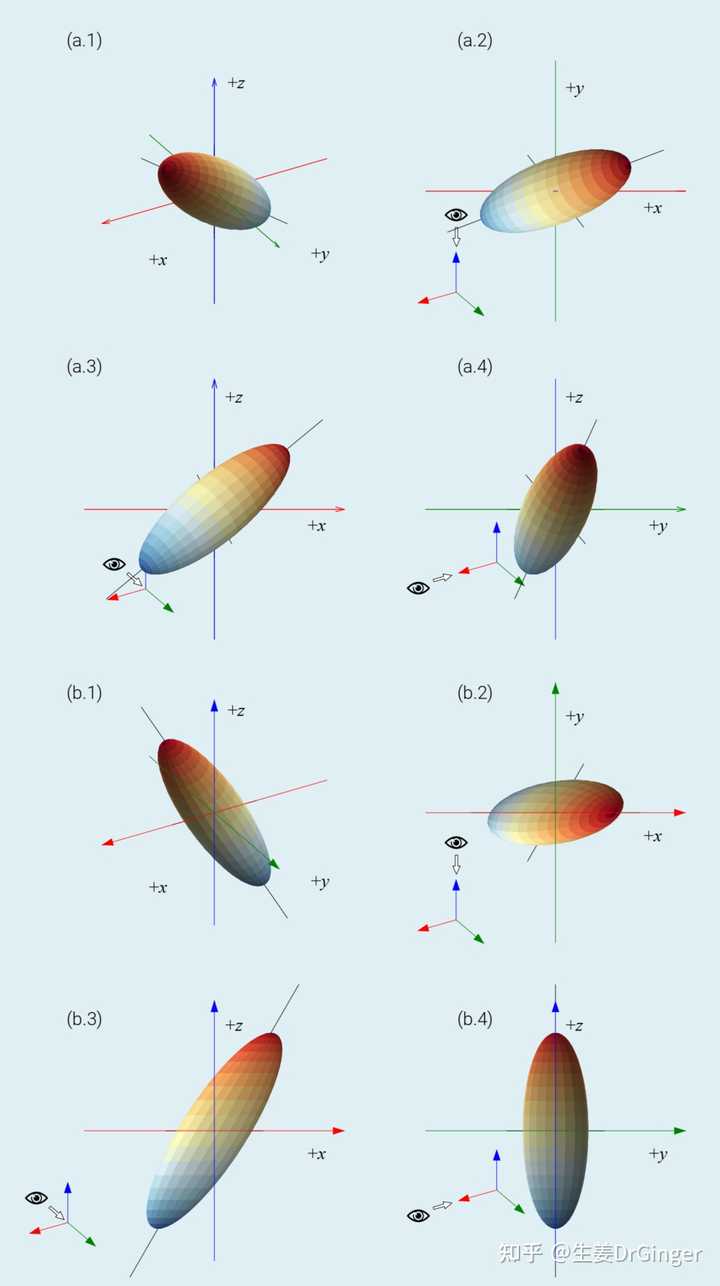
RGB 立方体框线； (a) 绕 x 轴旋转； (b) 绕 y 轴旋转

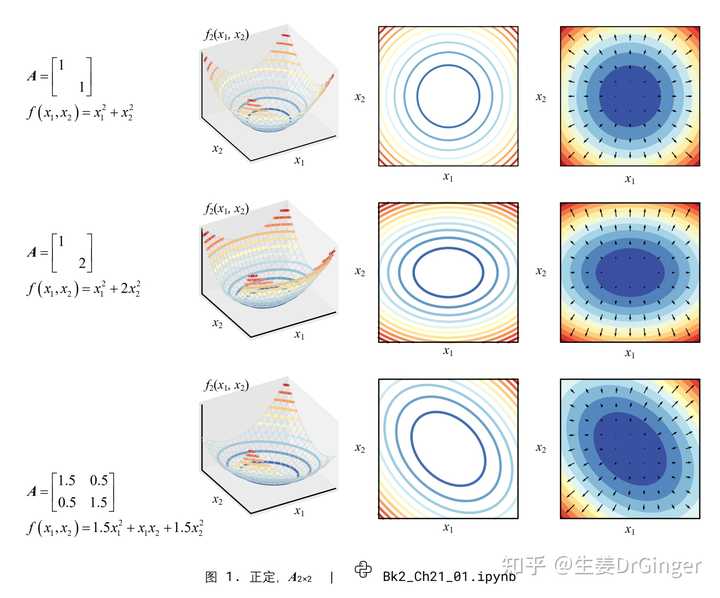
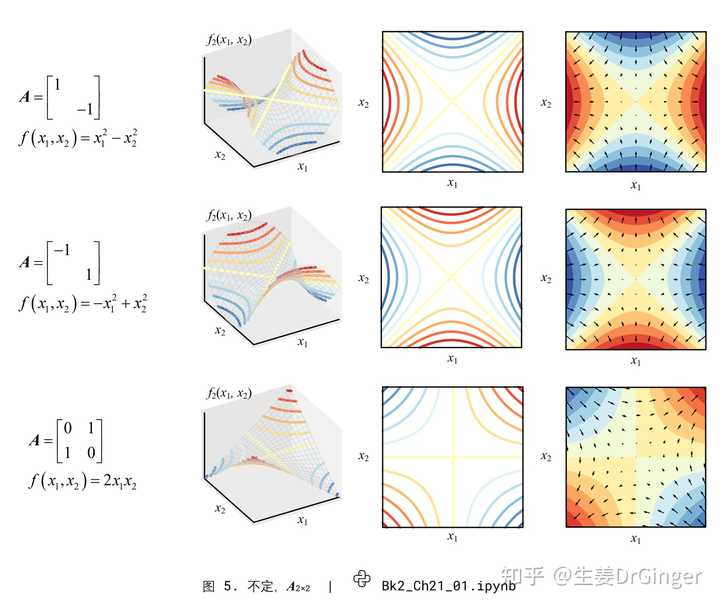
单位球几何变换： (a) 先缩放、再三轴旋转； (b) 先缩放、再沿 x 剪切二次型 (Quadratic Form)，可视化二元、三元二次型正定性

切豆腐，展示正定性

最后，要提一嘴，《可视之美》是开源“鸢尾花书”的第2本。目前7册鸢尾花书均开源
任何有关鸢尾花书问题，请参考：

正好最近研究了一些心形曲线，罗列一些。心形曲线的共同特点是都是偶数次的代数曲线。
二次心形曲线：
直角坐标方程： x^{2}+y^{2}-\left|x\right|y=1

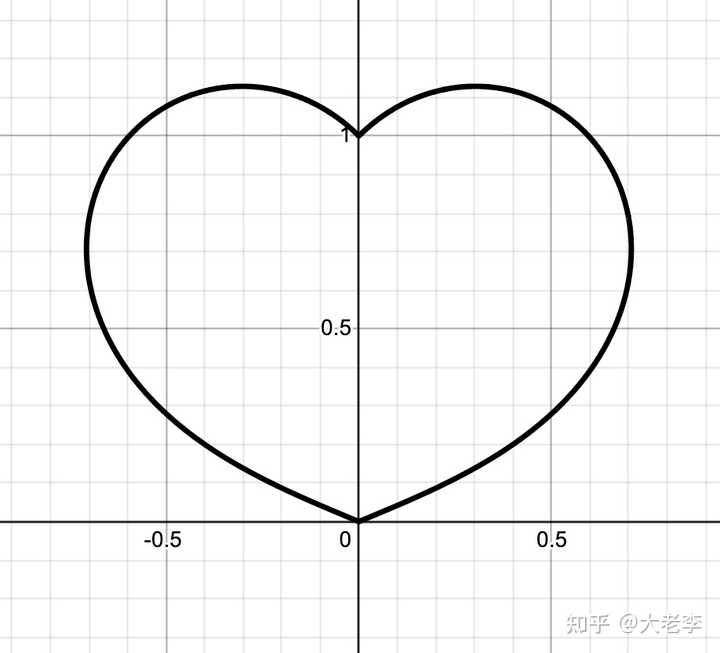
四次心形曲线：心脏线：
直角坐标方程： \left(x^{2}+y^{2}+y\right)^{2}=x^{2}+y^{2}
极坐标方程： r^2=1-\sin(\theta)
这是大家最熟悉的心形线，传说中笛卡尔发了这个方程向心仪的异性示好。

另一条四次心形线
直角坐标方程： (x^{2}+y^{2})^{2}+(|x|-y)^2-2y^2=0
极坐标方程： r^2=|\sin(2\theta)|-\cos(2\theta)
这条心形线是我最近“发现”的。详情见：大老李：疑似新型心形曲线的后续

六次曲线：
直角坐标方程： \left(x^2+y^2-1\right)^3-x^2 y^3=0 \text {. }

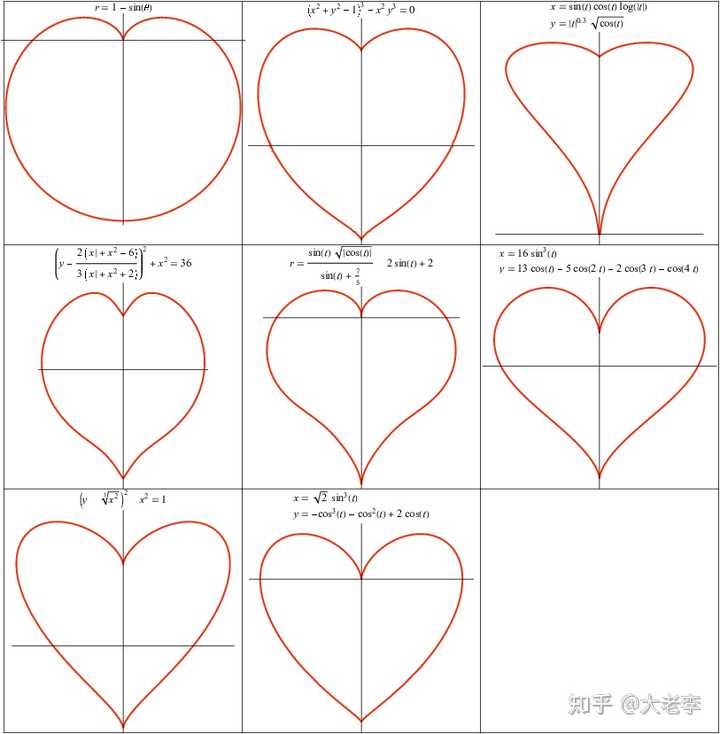
其他一些心形曲线：

图片来自 https://mathworld.wolfram.com/HeartCurve.html一些异形曲线：
猫脸线：\left(x^{4}+y^{4}+y\right)^{4}=x^{4}+y^{4}

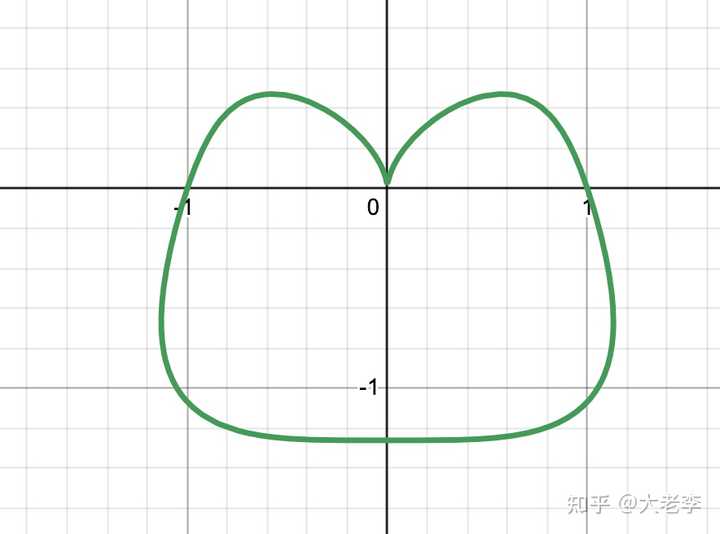
“苹果线”：\left(x^2+y^2\right)^{\frac{4}{3}}-4 y\left(x^{\frac{2}{3}}+y^{\frac{2}{3}}\right)-4 x^{\frac{2}{3}}=0

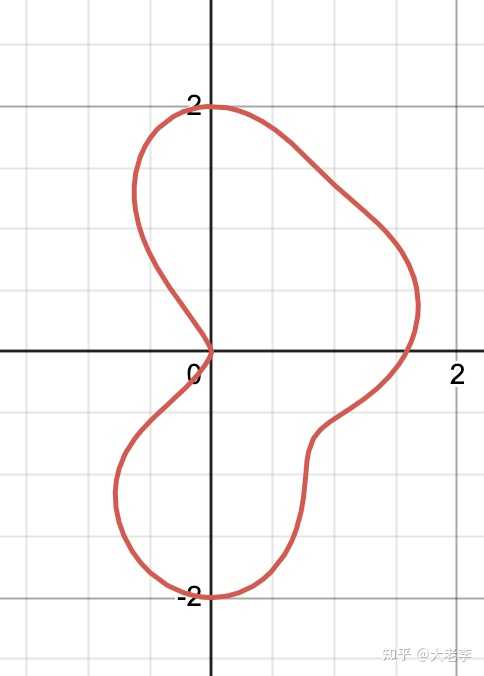
\left(x^{2}+y^{2}\right)^{3}-4y\left(x^{3}+y^{3}\right)-4x^{3}=0 ：(这是什么线？）

以上大多数图片用Desmos生成，它用来画曲线还是很方便的。我把这些曲线的desmos链接也共享在这里：https://www.desmos.com/geometry/q6tikoawpj

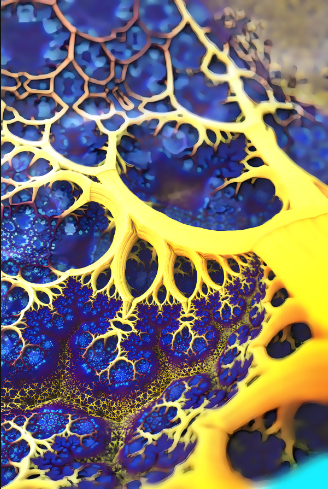
分形
几乎所有漂亮的几何图都可以概括在分形里。

分形各种维数的组合，弄出的动画非常牛逼。
分形通常被定义为"一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都(至少近似地)是整体缩小后的形状"，即具有自相似的性质。”
分形几何不仅展示了数学之美，也揭示了世界的本质，还改变了人们理解自然奥秘的方式；
世界是非线性的，分形无处不在。分形几何学不仅让人们感悟到科学与艺术的融合，数学与艺术审美的统一，而且还有其深刻的科学方法论意义。

[收藏本文] 【下载本文】

自然科学最新文章

海南一村民被眼镜王蛇咬死，多名消防员和村

有哪些不起眼的牢底坐穿兽？

美国耕地面积比中国大，可为什么粮食产量不

如何看待同济大学2024国家科技三大奖颗粒无

加:2024-03-10 13:41:00 更:2024-03-10 13:45:41

股票涨跌实时统计涨停板选股分时图选股跌停板选股 K线图选股成交量选股均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

网站联系: qq:121756557 email:121756557@qq.com 天天财汇