| |
|
|
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 自然科学 -> 为什么说正方形是特殊的矩形，却不说圆是特殊的椭圆？ -> 正文阅读 |
|
|
[自然科学]为什么说正方形是特殊的矩形，却不说圆是特殊的椭圆？ |
| [收藏本文] 【下载本文】 |
|
大学后就没碰过数学了，纯门外汉疑惑。 因为小学还是初中教材上明确提到过正方形是特殊的矩形，但是高中课本里从来没有说过圆是特殊的椭圆，但是圆难道不是一个… |
|
圆当然是特殊的椭圆。 但是关于椭圆的学科太难了。 我们说正方形是特殊的矩形时，往往是要把正方形的性质一般化，得到所谓的“通式”。 所以当我们说圆是特殊的椭圆时，则是要把圆的性质一般化。所以我们发现，半径为r的圆就是半长轴a和半短轴b相等的椭圆，椭圆的面积公式相比也一定就是 π∗ab" role="presentation">π?ab\pi*ab 吧！ 经过验证，确实是。我们成功将半径、面积一般化了，只要再把周长一般化，那么我们就可以很轻松地说圆是特殊的椭圆了。 那么顺利成章，椭圆的周长公式就是......，欸，不对，圆的周长公式 2πr" role="presentation">2πr2\pi r 中只有一个r，这要怎么分。平均分？ π（a+b)" role="presentation">（π（a+b){\pi（a+b)} ?经过验证，不对。然后人们开始了漫长的求椭圆周长的公式。 它等于 4a∫0π21−(1−a2b2)sin2θdθ" role="presentation">4a∫0π21?(1?a2b2)sin2θdθ4a\int_{0}^{\frac{\pi}{2}}\sqrt{{1-(1-\frac{a^2}{b^2}})sin^2\theta} d\theta 这个积分积不出来，原函数是个超越函数，最后结果只能用级数来表示。由此诞生了一个数学分支叫做椭圆积分。你把a=b带进去就可以得到 l=2a×π" role="presentation">l=2a×πl=2a\times\pi ,此时a就是圆的半径r，即圆的周长公式。 所以当我们把圆称作特殊的椭圆时，往往就是要涉及椭圆积分了，它太难了，大部分人学不到这里。 最后说一说为什么椭圆周长计算这么复杂，或者说特殊。这与 π" role="presentation">π\pi 有关系， π" role="presentation">π\pi 是圆的周长与直径之间的比例，它一开始就是用圆定义的。我们可以简单的设想到，一个给定的椭圆，其周长一定是与a和b有关系的，但是这个比值显然不是π" role="presentation">π\pi，每个给定a、b值的椭圆都有一个自己的“椭圆周率”，我们在把圆一般化的过程中，需要把 π" role="presentation">π\pi 给一般化了。但是显然我们无法直接知道每个椭圆自己的椭圆周率，它有无数个，所以我们需要借助已知的 π" role="presentation">π\pi 来架桥。当然这种说法并不严谨，只是可以用来简单思考椭圆与圆的关系。 |
|
说圆是特殊的椭圆可以，但某些相关定义会超出高中的处理能力。 比如，椭圆的第一定义：到两个点距离之和恒定的点的集合，这就让椭圆有两个焦点。如果是圆，就相当于椭圆的两个焦点重合了，焦距为0。不过这也不太难理解。 比较灾难的是第二定义，普通的圆都不适合第二定义。 椭圆是到定点的距离和定直线的距离之比（离心率）小于1的点的集合。这个定义可以让双曲线、抛物线、椭圆有良好的中间渐变。但是这个定义下的圆却是退化的，它成为缩在焦点处，半径为零的一个点。 要么是，你的准线得放在无穷远处。 总之，把圆放在圆锥曲线第二定义下，有一堆麻烦事。干脆不去讨论这样的边界情况。 |
|
主要看你研究的内容吧，如果你只是关注形如 x2/a2 + y2/b2 = 1 的方程那两者是统一的，但考虑准线的话就不行了。怎么分类不见得是个硬性的规定，不像高中可能就一本教材，为了高考统一标准，很多专业数学教材对符号和术语都有作者自己的微调。 |
|
正方形是特殊的长方形，而且长方形的性质也没有那么差，把正方形的条件弱化为长方形不会丢失太多信息，所以会经常说正方形是特殊的长方形。 圆当然可以是特殊的椭圆，但是椭圆的性质相比圆来说实在是太差了，把圆当成椭圆处理会失去非常多信息，所以不太提及圆是特殊的椭圆。 |
|
先说答案，圆是特殊的椭圆。由椭圆的定义，当定点F1和F2无限接近，直至重合的时候，平面内点到F1和F2的距离和便成为了直径的长度，椭圆也就成为了圆。另一种解释，则是离心率越小，椭圆会越接近于圆。 之所以会耳熟能详正方形是特殊的长方形，主要是由于平行四边形是初中必学的知识点，印象会更为深刻。当强调正方形是特殊的矩形时，也是因为会存在考察正方形一些性质的时候，会引用到长方形的性质，比如：对角线相等等。 相比之下，椭圆作为平面几何的基础是高中数学的重点教学内容，也是难点。部分伙伴，直到高中毕业，可能对椭圆、双曲线这些知识，都没有学明白、学透彻。对于圆是一种特殊的椭圆这种说法，老师在上课的时候，基本都会在讲到离心率e的时候，有所提到的。只不过，圆是特殊椭圆这个知识点的考察，远不会像正方形是特殊长方形这个知识点考察的频繁，因而对此印象可能并不会特别深刻。 总的来说，知识都是会随着时间流逝而出现淡忘的，尤其是对一些当年本就没有学明白的内容。当年读书的时候，强调要打好基础，也是为了将来某天即便是遗忘了，通过查找资料也能立刻回忆起来，重新为自己所使用。 |
|
椭圆也不够本质，得说圆是退化了的圆锥曲线 为什么说退化？因为没准线 |
|
当然是。斜着看(平行透视)，正方形变矩形，圆变椭圆，自然指数曲线变其它指数曲线，自然对数曲线变其它对数曲线。 |
|
|
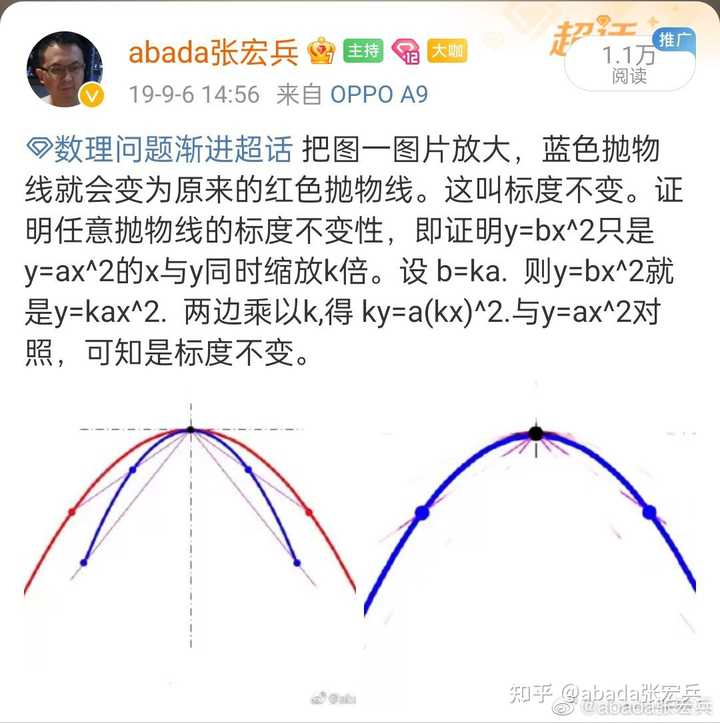
圆变成椭圆，也可以说是因为把圆的横向、纵向，仅一个缩放，或者横、纵缩放不一致形成的。 上面的指数函数变化也是如此。 世界上任何两事物，可以归为同类，也可以归为异类，这取决于人为的分类法。 补充：标度不变性 如果把圆，纵横缩放比例一样，那么世界上的圆都一样，都可以经过缩放而重合。从这个意义上说 世界上只有一个圆。这叫标度不变性。 悬链线也有标度不变性，下面的图一与图二的悬链线，看上去如此不同，其实不然。盯住图二悬链线的底部，然后图片放大看，即图三，与图一的悬链线完全一样： |
|
|
除了圆，y=kx^a的幂函数，相同的a，而k不同，也都有标度不变性。所以也可以说：世界上的抛物线只有一个。（就像圆那样） |
|
|
|
|
|
|
|
咋不说呢？圆就是特殊的椭圆啊。 人造地球卫星的椭圆轨道和圆形轨道。不就是这种情况吗？ |
|
没毛病，圆就是特殊的椭圆。而且圆也是特殊的圆锥曲线，水平面截圆锥即可。 高中的定义什么的本来就很死板，不用想太多。 |
|
因为正方形是特殊的矩形是小学级别的知识，而圆是特殊的椭圆是高中级别知识。 小学级别知识人尽皆知家喻户晓，自然容易传播，高中知识知道的人少，装X都装不出效果 |
|
圆是不是椭圆不太好说。因为椭圆有准线 x=a2c" role="presentation">x=a2c\displaystyle x=\frac{a^2}{c} ，且椭圆上一点 P" role="presentation">PP 到焦点 F(c,0)" role="presentation">F(c,0)F(c,0) 的距离|PF|" role="presentation">|PF|\left| PF \right| 与准线的距离 |PH|" role="presentation">|PH|\left| PH \right| 满足 |PF||PH|=e" role="presentation">|PF||PH|=e\displaystyle\frac{\left| PF \right|}{\left| PH \right|}=e 即椭圆的第二定义。 而我们知道圆的离心率是等于0的，圆的“焦点”是圆心 O" role="presentation">OO ，你是找不到一条直线使得 |PO||PH|=0" role="presentation">|PO||PH|=0\displaystyle\frac{\left| PO \right|}{\left| PH \right|}=0 即圆不满足椭圆的第二定义。 |
|
如果认为圆是特殊的椭圆，那就要承认线段是特殊的椭圆。 |
|
你应该问的是“为什么不常听说圆是特殊的椭圆？” 在数学上，“特例”是有明确含义的。“正方形是矩形的特例”是因为当矩形的长宽相等时，“该矩形”可以称为“正方形”。同样的，当某个椭圆的通式： x2a2+y2b2=1" role="presentation">x2a2+y2b2=1\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 中的a,b相等时，“该椭圆”则称为“圆”（方程自然就成了圆方程： x2+y2=r2" role="presentation">x2+y2=r2x^{2}+y^{2}=r^{2} ，椭圆的长轴，短轴自然也就”合并“为圆半径）。 那你为什么会有那样的疑问呢？首先当然是因为你看过的数学书上可能没说这一点（这很正常，况且你估计看的数学书也不多）。另外，我想可能有下面两个原因： 一是数学教学中讨论椭圆时距离讲解圆时间已经比较长了，而矩阵与正方形几乎是同时出现在小学课本中的，讲正方形是矩形的特例很自然。二是日常生活中说到”椭圆“的机会比说到矩形或正方形的机会少得多，当然也很少有人去说圆是椭圆的特例。 顺便说一句，从”现象“反推出”原因“在目前人工智能推理系统中是个非常重要，但也非常难的问题。要想实现”可解释“的AI，这很关键。当然上面我说的算不上”推理“，只是因你的问题产生的联想。 |
|
所以兩條相交的直線也是特殊的雙曲線，因為這兩條直線上任意點到他倆的交點的距離減掉自身都是0，所有的0都相等。 題主您看看這合理嗎。 |
|
因为椭圆、双曲线、抛物线、圆都是特殊的二次曲线。 |
|
正方形是特殊的矩形的意思是，正方形拥有矩形所有的性质，特殊在他长宽相等 圆不是特殊的椭圆的原因是，圆不符合椭圆的定义：也就是说圆压根就不是椭圆。所以圆不是特殊的椭圆 关于椭圆的定义有几种，现取一种：第一定义 平面内与两定点F1 、F2 的距离的和等于常数2a （2a＞|F1F2|）的动点P的轨迹叫做椭圆。 两个定点，所以圆压根不是椭圆，他怎么是特殊的椭圆去啊 |
|
圆和椭圆都是超越曲线。但是圆的很多超越曲线的性质的超越部分可以化简成一个超越常数，也就是圆周率，导致这些性质看起来都是代数性质。时间长了大家都忘了圆周率是个超越常数，以为圆是一个代数曲线，让小学生就开始学习圆。 椭圆就没这么好化简，处处都超越，自然是学超越函数的时候才学习。于是圆和椭圆就显得关系没那么大了。 |
|
矩形的定义之一是“四个角都是直角的四边形”，符合这个特征，即属于矩形范围之内。 椭圆的定义之一是：“到两个定点距离之和相等的点的集合”，粗俗点说，圆有一个心，椭圆有两个心。从这个角度看，圆和椭圆并不是一个东西； 但从解析式上看，又允许两个定点重合，这么看，说“椭圆是特殊的圆”也没毛病。 |
|
有一个角是直角的菱形是正方形 邻边相等的矩形是正方形 椭圆是有长短轴，焦点焦距及准线的 但是圆只有圆心及半径，这是两个完全不同的封闭曲线 |
|
定义不同吧。 矩形是有一个角是直角的平行四边形，或者四个角都是直角的四边形。正方形就是矩形加一条邻边相等。 椭圆是到两点距离和为定值的点的轨迹。圆是到一点距离为定值的点的轨迹。两个点和一个点不同吧。 |
|
非要这么说也行，毕竟都是切圆锥切出来的 |
|
在一般情况下，正方形被描述为特殊的矩形，而不常说圆是特殊的椭圆，这主要是因为数学和几何学的传统以及这些形状在教育和日常应用中的常见用法。以下是几个关键原因： 数学定义和教育：在数学和几何教育中，矩形和正方形通常作为初学者学习的基本几何形状。正方形被定义为所有四边相等的矩形，这种定义自然而然地将正方形归类为矩形的一种特殊情况。这种分类帮助学生理解几何形状之间的关系，并构建起从最简单形状到更复杂形状的知识体系。相比之下，圆和椭圆虽然在数学上圆是一种特殊的椭圆（两个焦点重合的椭圆），但在教育过程中，它们通常被作为两种截然不同的基本形状教授，这反映了教育上的侧重点和简化。形状的几何属性：正方形和矩形之间的区别相对较小，且它们共享许多属性（例如，都有四个角和四条边，且每个内角都是90度）。这种近似性使得将正方形视为矩形的一个特例在逻辑上更容易为人接受。而圆形作为一个完全对称的形状，其与椭圆的外观和几何属性差异更加明显，尽管数学上圆是特殊的椭圆，但在日常使用中，人们倾向于根据它们的直观外观和用途来区分它们，而不是依据它们之间的数学关系。应用和直觉：在日常应用中，正方形和矩形因其简单和实用性而广泛应用于建筑、设计和日常物品中。它们的区别往往不如圆形和椭圆在视觉和应用上的区别那么重要。因此，将正方形视为矩形的特例在实际应用中是有意义的，而圆形和椭圆则因其不同的应用和性质（例如，在光学、天文学和艺术设计中）而被视为截然不同的形状。 综上所述，将正方形描述为特殊的矩形而不常将圆描述为特殊的椭圆，反映了数学定义、教育侧重点、几何属性以及形状在日常生活中应用的差异。这种区分方式帮助人们在不同的上下文中更有效地理解和使用这些几何形状。 |
|
因为要把圆锥曲线分成互斥的五类。 偏心率在 (0, 1) 的才叫椭圆。如果偏心率是 0 也叫椭圆，那么偏心率为 1 的抛物线要不要算椭圆呢？ |
|
答案是日常生活中长方形比正方形多见到，圆形比椭圆形多见到。 长方形多见、正方形相对少见，对吧？所以用多见的事物，解释少见的事物，比较容易被人接受。 圆形日常生活中比较多见，椭圆形日常生活中见得比较少，常见的事物解释中含包含一个少见的事物，那么这个解释就不容易被大多数人所接受、理解。 这是我一个外行人主观的想法，是一个数学差生的主观臆断。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
结论:圆不是特殊的圆. 椭圆（Ellipse）是平面内到定点F1、F2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，F1、F2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a>|F1F2|）。[1] 那些认为圆是椭圆的人，认为圆是F1和F2两个点重合到一起的特殊椭圆。而圆边上的任意一点P到重合的F1和F2之和也是一个常数。 问题是讨论的圆和椭圆是平面几何的概念啊！不是立体几何。点在平面上具有唯一性，不可能又叫F1又叫F2。 |
|
|
| [收藏本文] 【下载本文】 |
| 自然科学 最新文章 |
| 海南一村民被眼镜王蛇咬死，多名消防员和村 |
| 有哪些不起眼的牢底坐穿兽？ |
| 美国耕地面积比中国大，可为什么粮食产量不 |
| 如何看待同济大学2024国家科技三大奖颗粒无 |
| 假如航母被蓝鲸全速前进撞一下会怎么样？ |
| 你见过最狠的SCI评论是什么? |
| 你在实验室最惊险的瞬间是什么？ |
| 牛顿生活在中国，会有什么成就？ |
| 虎鲸为什么不吃人？ |
| 数学为什么这么可笑？ |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |