[自然科学] 你有没有在某个瞬间觉得数学是美的，或者被数学震撼到？

天天财汇购物网址万年历小说 | 三峰软件小游戏视频

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

首页淘股吧股票涨跌实时统计涨停板选股股票入门股票书籍股票问答分时图选股跌停板选股 K线图选股成交量选股 [平安银行]

股市论谈均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

商业财经科技知识汽车百科工程技术自然科学家居生活设计艺术财经视频游戏--

天天财汇 -> 自然科学 -> 你有没有在某个瞬间觉得数学是美的，或者被数学震撼到？ -> 正文阅读

[自然科学]你有没有在某个瞬间觉得数学是美的，或者被数学震撼到？

[收藏本文] 【下载本文】

数学其实不算是我擅长的科目也许是因为智商不够吧但是我偶尔在某个瞬间感到数学很美，很宏大，仿佛包含了整个世界小学初中的时候不过觉得是一种科目高中…

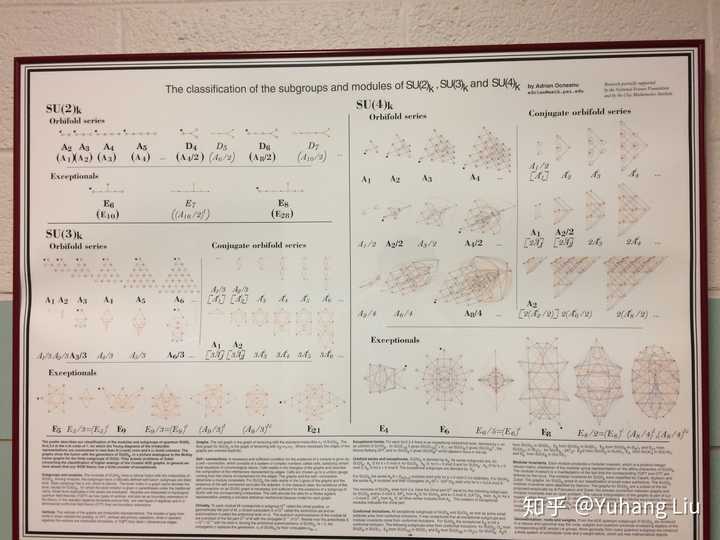
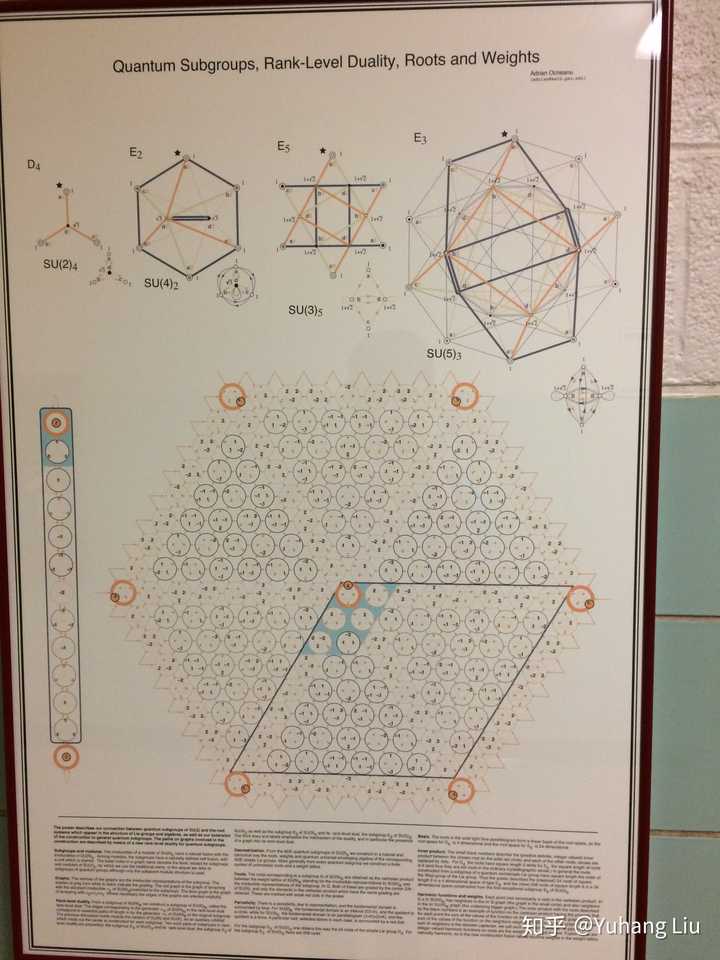
Cartan对单李代数的分类，A B C D 四族典型群和E F G 三族例外单李群，以及相应的Dynkim diagram，根系图（图片网上搜吧），当然还有这些李群的结构和表示论。非常漂亮的一套理论。我希望有生之年也能做出这样精美的工作。
我在我们系里还见过量子群的根系图，非常对称，等我回到系里再拍张照片传上来。

Vasc Inequality
a,b,c∈R,prove that:(a2+b2+c2)2≥3(a3b+b3c+c3a)" role="presentation">a,b,c∈R,prove that:(a2+b2+c2)2≥3(a3b+b3c+c3a)a,b,c\in\mathbb{R},\text{prove that}:(a^2+b^2+c^2)^2\ge3(a^3b+b^3c+c^3a)
第一下惊艳是这个简短暴力却优美的证明：
Proof : (a2+b2+c2)2−3(a3b+b3c+c3a)=12((a2−2ab+bc−c2+ca)2+(b2−2bc+ca−a2+ab)2+(c2−2ca+ab−b2+bc)2)≥0,Q.E.D" role="presentation">Proof : (a2+b2+c2)2?3(a3b+b3c+c3a)=12((a2?2ab+bc?c2+ca)2+(b2?2bc+ca?a2+ab)2+(c2?2ca+ab?b2+bc)2)≥0,Q.E.D\begin{align} \text{Proof : }&\left(a^{2}+b^{2}+c^{2}\right)^{2}-3\left(a^{3} b+b^{3} c+c^{3} a\right)\\ =& \frac{1}{2}\left(\left(a^{2}-2 a b+b c-c^{2}+c a\right)^{2}+\left(b^{2}-2 b c+c a-a^{2}+a b\right)^{2}\\ +\left(c^{2}-2 c a+a b-b^{2}+b c\right)^{2}\right) \geq 0,Q.E.D\end{align}
第二下惊艳是这个不等式的取等条件：
除了常规的 a=b=c" role="presentation">a=b=ca=b=c 外，还有 a:b:c=sin2⁡4π7:sin2⁡2π7:sin2⁡π7" role="presentation">a:b:c=sin2?4π7:sin2?2π7:sin2?π7a : b : c=\sin ^{2} \frac{4\pi}{7} : \sin ^{2} \frac{2 \pi}{7} : \sin ^{2} \frac{\pi}{7} 或其轮换
意料之外的取等条件出奇的优美，也让这个问题很难用其他方法证明

在数学上面确实有很多让人震撼的结果，先说几个数论上面的例子吧： n" role="presentation">nn 表示正整数， p" role="presentation">pp 表示素数。
∑n≤x1n∼ln⁡(x),when x is sufficiently large." role="presentation">∑n≤x1n～ln?(x),when x is sufficiently large.\sum_{n\leq x}\frac{1}{n} \sim \ln(x), \text{when } x \text{ is sufficiently large.}
∑p≤x, p is prime1p∼ln⁡ln⁡(x), where x is sufficiently large." role="presentation">∑p≤x, p is prime1p～ln?ln?(x), where x is sufficiently large.\sum_{p\leq x, \text{ }p \text{ is prime}} \frac{1}{p} \sim \ln\ln(x), \text{ where } x \text{ is sufficiently large.}
简单来说，就是所有正整数的倒数和是发散的，所有素数的倒数和也是发散的。但是孪生素数的倒数和却是收敛的，极限称之为 Brun 常数（1919 年证明）。
∑p, p+2 are primes(1p+1p+2) is convergent." role="presentation">∑p, p+2 are primes(1p+1p+2) is convergent.\sum_{p,\text{ } p+2 \text{ are primes}} \bigg(\frac{1}{p}+\frac{1}{p+2}\bigg) \text{ is convergent.}
假设 pn" role="presentation">pnp_{n} 表示第 n" role="presentation">nn 个素数。
1940 年， Paul Erdos 证明了，存在 0<c<1," role="presentation">0<c<1,n 使得 pn+1−pn<c⋅ln⁡(pn)" role="presentation">pn+1?pn<c?ln?(pn)c 可以足够小，i.e.
lim infn→∞pn+1−pnln⁡(pn)=0." role="presentation">lim?infn→∞pn+1?pnln?(pn)=0.\liminf_{n\rightarrow \infty} \frac{p_{n+1}-p_{n}}{\ln(p_{n})} = 0.
2013 年，张益唐证明了 lim infn→∞(pn+1−pn)<7∗107," role="presentation">lim?infn→∞(pn+1?pn)<7?107,\liminf_{n\rightarrow\infty}(p_{n+1}-p_{n})\liminf_{n\rightarrow\infty}(p_{n+1}-p_{n})<7*10^7, 目前七千万这个数字已经被降低到 246。
后续持续更新。

列一个上周才听老师讲的吧: Ress=1ζK(s)=2r1(2π)r2h(K)R(K)w(K)|d(K)|" role="presentation">Ress=1ζK(s)=2r1(2π)r2h(K)R(K)w(K)|d(K)|Res_{s=1}\zeta_{K}(s)=\frac{2^{r_{1}}(2\pi)^{r_{2}}h(K)R(K)}{w(K)\sqrt{|d(K)|}}
zeta函数在1的留数竟然与类数、regulator(不知道这个词在中文里叫啥，各位知乎中文数学家们不要喷我啊)、判别式、单位根个数这些数域的整体的量联系在一起，，，据老师说，好像可以通过估计等式的左边来求出理想类群的类数 h(K)" role="presentation">h(K)h(K) ，，，
上课讲的一个小栗子，取 K=Q(−1)" role="presentation">K=Q(?1)K=\mathbb{Q}(\sqrt{-1}) ,则从上面的等式可以看出大家熟知的Leibniz（莱布尼兹）公式 1−13+15−17+19−⋯=π4" role="presentation">1?13+15?17+19??=π41-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots=\frac{\pi}{4} 实际上就蕴含了Gauss（高斯）整数环的类数为1，，，
补充几个:
(a,N)=1,A={p素数|p≡amodN)}" role="presentation">素数(a,N)=1,A={p素数|p≡amodN)}(a,N)=1,A=\{p素数|p\equiv a\mod N)\} ,则 A" role="presentation">AA 的Dirichlet密度 δ(A)=lims→1+∑p∈A1ps∑p1ps=1φ(N)" role="presentation">δ(A)=lims→1+∑p∈A1ps∑p1ps=1φ(N)\delta(A)=\lim_{s\rightarrow1^{+}} \frac{\sum_\limits{p\in A}\frac{1}{p^{s}}}{\sum\limits_{p}\frac{1}{p^{s}}}=\frac{1}{\varphi(N)}
F/Q" role="presentation">F/QF/\mathbb{Q} 是Galois扩张, 则δ(Split(F/Q))=1[F:Q]" role="presentation">δ(Split(F/Q))=1[F:Q]\delta(\mathrm{Split}(F/\mathbb{Q}))=\frac{1}{[F:\mathbb{Q}]}
两个Galois扩张 F1/Q,F2/Q" role="presentation">F1/Q,F2/QF_{1}/\mathbb{Q},F_{2}/\mathbb{Q} ，若在其中完全分裂的素数几乎相同,则两个扩张相等。

话说从中学到现在我被数学的美震撼过一次又一次，有的是因为精妙的技巧，有的是因为深刻的理论。例如，由于我本科的抽象代数课程是安排在大一第一学期的，我还记得那时被Galois Theory震撼的感觉（不过我真正的理解Galois Theory要到大三了...）。
这里我再举另外一个例子，也是个看起来比较神奇的东西。
假设我们有一个杂乱的毛线团。。

如果我们想知道他“具体的结构”，看起来这个问题有点痛苦。。
换个问题。假设我们考虑大型的社交网络，比如facebook。

我们想知道这个网络的结构，看起来也是一个不可能的问题。
现实生活中，我们可能会面临很多类似这种处理“非常复杂”的网络的问题，例如互联网，社交网络 ( 地球可是有70亿人 )，神经网络系统 ( 我们的大脑有近千亿个神经元 ) ，统计物理。
在纯数学研究中，这样的问题也很常见，例如，研究一个复杂的集合的各种性质 ( 比如一个经典问题，给定一个整数的子集，问里面包含多长的等差数列？ ) 。
Szemeredi告诉我们，这些问题通通都不是问题。
Szemeredi Regularity Lemma.
Given 0">ε>0" role="presentation">ε>0\varepsilon>0 and a positive integer m" role="presentation">mm, there exists an integer M" role="presentation">MM such that the following holds. If a graph G" role="presentation">GG has at least m" role="presentation">mm vertices, there exists an integer k" role="presentation">kk satisfies m≤k≤M" role="presentation">m≤k≤Mm\leq k\leq M , and a partition P" role="presentation">P\mathcal{P} of V(G)" role="presentation">V(G)V(G) with k" role="presentation">kk parts V1,V2,…,Vk" role="presentation">V1,V2,…,VkV_1,V_2,\dots,V_k , for every 1≤i<j≤k" role="presentation">1≤i<j≤k1\leq i<j\leq k , ||Vi|−|Vj||≤1" role="presentation">||Vi|?|Vj||≤1\big||V_i|-|V_j|\big|\leq 1 . For all but at most εk2" role="presentation">εk2\varepsilon k^2 pairs (Vi,Vj)" role="presentation">(Vi,Vj)(V_i,V_j) , for every subsets A⊆Vi" role="presentation">A?ViA\subseteq V_i and B⊆Vj" role="presentation">B?VjB\subseteq V_j with |A|≥ε|Vi|" role="presentation">|A|≥ε|Vi||A|\geq\varepsilon|V_i| and |B|≥ε|Vj|" role="presentation">|B|≥ε|Vj||B|\geq \varepsilon|V_j| , we have |e(A,B)|A|⋅|B|−e(Vi,Vj)|Vi|⋅|Vj||<ε" role="presentation">|e(A,B)|A|?|B|?e(Vi,Vj)|Vi|?|Vj||<ε\mathsf{e}(A,B) is the number of edges having one end vertex in A and one end vertex in B.
哲学的说，Szemeredi regularity lemma告诉我们，完全混乱是不可能的。对于一个非常混乱复杂的网络，他一定满足非常简单的规律。有多简单呢？对于一个复杂网络，我们可以相当快的 ( O(n^2) )得到它几乎所有的性质。Szemeredi本人也由于这个lemma（以及后续应用这个lemma得到的定理）获得了2012年的Abel奖。
所以从数学角度，最困难的问题其实是研究“稀疏”的网络。看起来复杂的东西其实都长一个样，看起来简单的反而各有各的不同。
至于看起来简单的，“稀疏”的网络，目前比较好的进展是Ben Green和陶哲轩证明的，如果这个稀疏网络长的和所有素数“差不多”，那么它满足和上面的“稠密的”复杂网络差不多的性质。Conlon, Fox, Zhao稍微推广了一下他们的结果。简单说，就是一个稀疏图的two-blow up要满足counting lemma。至于一般的稀疏图，目前还相当open。

看证明前：woc！？
看证明中：woc！！
看证明后：woc~
。
。
。
。
。
。
几个月后：trivial

Radon-Nikodym导数
如果测度 \mu 关于测度 \nu 绝对连续，那么存在一个函数 f 使得任意可测集 X
\mu(X)=\int_{X}fd\nu
且在测度\nu看来，f几乎处处唯一（即若两个函数都满足此条件，则他们几乎处处相等）
这个函数 f 称为\mu 对 \nu 的Radon-Nikodym导数，记作 \frac{d\mu}{d\nu} 。
对于学数学的同学来说，这个定理可能太简单了，没有什么奇怪的，但这个东西在物理上很不一般，因为物理上有很多密度，他们实际上都是Radon-Nikodym导数，这其中也包括概率密度，当然量子力学的波函数也是Radon-Nikodym导数，相当于概率密度开方再乘以相位。

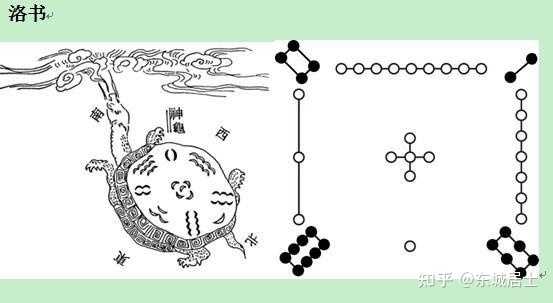
洛书，古称龟书，由于在古代传说中有神龟出于洛水，其甲壳上有此图象而得名。洛书的结构是戴九履一，左三右七，二四为肩，六八为足，以五居中.

洛书
虽然古人将洛书说得神乎其神，其实说白了洛书就是一个三阶幻方.

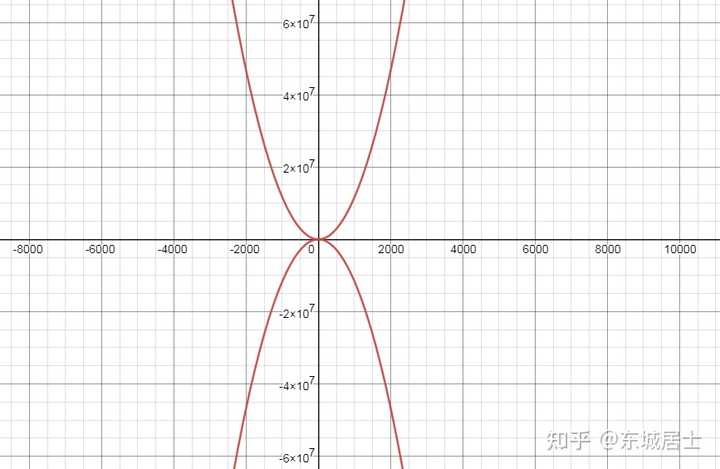
最简单的三阶幻方
若这个幻方从 9 开始，按顺时针每两个数字组成一个数，则可以得到 8 个数，分别为：
~~~~~~92,~27,~76,~61,~18,~83,~34,~49.
若这个幻方从 9 开始，按逆时针每两个数字组成一个数，也可以得到 8 个数，分别为：
~~~~~~94,~43,~38,~81,~16,~67,~72,~29.
这两组数满足
~~~~92+27+76+61+18+83+34+49
=94+43+38+81+16+67+72+29.
其实这并没有什么神奇的，因为这两组数的各位数和十位数都是 1,2,3,4,6,7,8,9 . 但是令人意想不到的是这两组数还满足
~~~~92^2+27^2+76^2+61^2+18^2+83^2+34^2+49^2
=94^2+43^2+38^2+81^2+16^2+67^2+72^2+29^2.
更令人惊讶的是
~~~~92^3+27^3+76^3+61^3+18^3+83^3+34^3+49^3
=94^3+43^3+38^3+81^3+16^3+67^3+72^3+29^3.
所以这是一组非常神奇的数字！但是
~~~~92^4+27^4+76^4+61^4+18^4+83^4+34^4+49^4
\ne94^4+43^4+38^4+81^4+16^4+67^4+72^4+29^4.
那是否还有具有类似性质的数呢？答案是：有！比如下面这两组数
~~~~~~~~~~~~1 ,~ 19 ,~ 20,~ 51 ,~ 57 ,~ 80,~ 82
~~~~~~~~~~~~2,~12,~31,~40,~69,~71,~85.
它们满足
~~~~1 + 19 + 20 + 51 + 57 + 80+ 82
=2 + 12 + 31 + 40 + 69 + 71 + 85,
~~~~1^2 + 19^2 + 20^2 + 51^2 + 57^2 + 80^2+ 82^2
=2^2 + 12^2 + 31^2 + 40^2 + 69^2 + 71^2 + 85^2,
~~~~1^3 + 19^3 + 20^3+ 51^3 + 57^3 + 80^3+ 82^3
=2^3 + 12^3 + 31^3 + 40^3 + 69^3 + 71^3 + 85^3,
~~~~1^4 + 19^4 + 20^4+ 51^4 + 57^4 + 80^4+ 82^4
=2^4 + 12^4 + 31^4 + 40^4 + 69^4 + 71^4 + 85^4,
~~~~1^5 + 19^5 + 20^5+ 51^5 + 57^5 + 80^5+ 82^5
=2^5 + 12^5 + 31^5 + 40^5 + 69^5 + 71^5 + 85^5,
~~~~1^6 + 19^6 + 20^6+ 51^6 + 57^6 + 80^6+ 82^6
=2^6 + 12^6 + 31^6 + 40^6 + 69^6 + 71^6 + 85^6.
第一次看到这么神奇的数时，我简直被震撼到了！数学也太好玩太美了！
其实上述两组数都是所谓的等幂和问题的解. 等幂和问题也叫 Prouhet-Tarry-Escott 问题，即对任意的正整数 n ，要找两组不同的整数
~~~~~a_1,~a_2,\cdot\cdot\cdot, ~a_m,~~~~~~b_1,~b_2,\cdot\cdot\cdot, ~b_m.
使得当 1\leq k\leq n 时，有
~~~~~~~~~~~~~~~~~~~~~\sum_{i=1}^{m}{a_{i}^{k}}=\sum_{i=1}^{m}{b_{i}^{k}}.
1935 年，数学家 Wright 猜测：对任意的正整数 n ，都存在两组不同的整数
~~~~a_1,~a_2,\cdot\cdot\cdot, ~a_{n+1},~~~~~~b_1,~b_2,\cdot\cdot\cdot, ~b_{n+1}.
使得当 1\leq k\leq n 时，有
~~~~~~~~~~~~~~~~~~~~~\sum_{i=1}^{n+1}{a_{i}^{k}}=\sum_{i=1}^{n+1}{b_{i}^{k}}.
对于等幂和问题，一般来说 n 越大越困难. 1999 年，Kuosa, Meyrignac 和陈漱文借助计算机第一次解决了 n=11 的等幂和问题，他们找到了两组数
1, 12, 25, 66, 91, 130, 174,213, 238, 279, 292, 303,
4, 6, 31, 58, 105, 117, 187,199, 246, 273, 298, 300.
使得当 1\leq k\leq11 时，满足
~~~1^k+12^k+25^k+66^k+91^k+130^k+174^k+213^k+238^k+279^k+292^k+303^k
=4^k+6^k+31^k+58^k+105^k+117^k+187^k+199^k+246^k+273^k+298^k+300^k.
这是目前能解决的 n 最大的等幂和问题，显然这两组数同时加上一个整数，得到的两组数仍然满足上述结论，这样的解称为是等价的. 对于 n=11 ，等幂和问题等价的解显然有无穷多组，但是否还有不等价的解呢？2007 年英国数学家 Broadhurst 运用中国剩余定理找到了第二组不等价的解. 由于这样的解要满足太多的等式，所以我们可能会很自然地想这样的解肯定十分稀少. 但令人意想不到的是，2008 年，Chouhdry 和 Wroblewski 借助椭圆曲线证明了 n=11 的等幂和问题有无穷多个不等价的解！这个看似与椭圆曲线毫无关系的问题，最后却是用椭圆曲线解决的，这让人觉得不可思议！下面我们一起看看这一精彩的解答方法.
首先，当 k=2,4,6,8,10 时，若有
~~~~~~~~~~~~~~~~~~\sum_{i=1}^{6}{A_{i}^{k}}=\sum_{i=1}^{6}{B_{i}^{k}}.
则数组
\{\pm A_1,\pm A_2,\cdot\cdot\cdot, \pm A_6\},~~~\{\pm B_1,\pm B_2,\cdot\cdot\cdot, \pm B_6\}.
满足方程
~~~~~~~~~~\sum_{i=1}^{12}{a_{i}^{k}}=\sum_{i=1}^{12}{b_{i}^{k}}~~(1\leq k\leq11).
即我们仅需求方程
~~\sum_{i=1}^{6}{A_{i}^{k}}=\sum_{i=1}^{6}{B_{i}^{k}}~~~(k=2,4,6,8,10)
的整数解. 设
A_1 = 2xy + xz + 2yz ? 7z^2, ~~~B_1 = 2xy + 2xz + yz ? 7z^2,
A_2 = 2xy ? xz ? 2yz ? 7z^2, ~~B_2 = 2xy ? 2xz ? yz ? 7z^2,
A_3 = 2xy ? 2xz + yz + 7z^2, ~~B_3 = 2xy ? xz + 2yz + 7z^2,
A_4 = 2xy + 2xz ? yz + 7z^2, ~~B_4 = 2xy + xz ? 2yz + 7z^2,
A_5 = 3xz + 5yz, ~~~~~~~~~~~~~~~~~~~~~~B_5 = 5xz + 3yz,
A_6 = 5xz ? 3yz, ~~~~~~~~~~~~~~~~~~~~~~B_6 = 3xz ? 5yz.
我们记
~~~~~~~~~~~~~~S_k=\sum_{i=1}^{6}{A_{i}^{k}}-\sum_{i=1}^{6}{B_{i}^{k}}.
经过复杂的计算可得
S_2=S_4=0,
S_6 = 4320xyz^4(x ? y)(x + y)f(x,y,z),
S_8 = 5376xyz^4(x ? y)(x + y)f(x,y,z)(8x^2y^2 + 37x^2z^2 + 37y^2z^2 + 98z^4)
S_{10} = 10080xyz^4(x ? y)(x + y)f(x,y,z)(665y^4z^4 + 248x^2y^4z^2 + 32x^4y^4+
~~~~~~~~~~~3038y^2z^6 + 2384x^2y^2z^4 + 248x^4y^2z^2 + 4802z^8+ 3038x^2z^6 + 665x^4z^4)
其中
f(x,y,z)=8x^2y^2 ? 17x^2z^2 ? 17y^2z^2+ 98z^4.
故问题转化为求方程 f(x,y,z)=0 的整数解. 我们令
~~~~~~~~~~~x=Uz,~~~~~~y=\frac{Vz}{8U^2-17}.
带入方程 f(x,y,z)=0 ，可得
~~~~~~V^2=136U^4-1073U^2+1666.

曲线 V^2=136U^4-1073U^2+1666
由于当 U=\pm1 时，
V^2=136-1073+1666=729=27^2.
从而可知曲线
~~~~~~V^2=136U^4-1073U^2+1666
有有理点
(1,27),~(1,-27),~(-1,27),~(-1,-27).
我们又令
X=\frac{251X+3Y-206690}{89X+3Y-36410},
Y=\frac{243X^3-766260X^2+312978600X-9256500Y+59116365000}{(89X+3Y-36410)^2}.
带入方程
~~~~~~V^2=136U^4-1073U^2+1666,
得椭圆曲线
E:Y^2 = X^3 + X^2 ? 1290080X + 556370100.

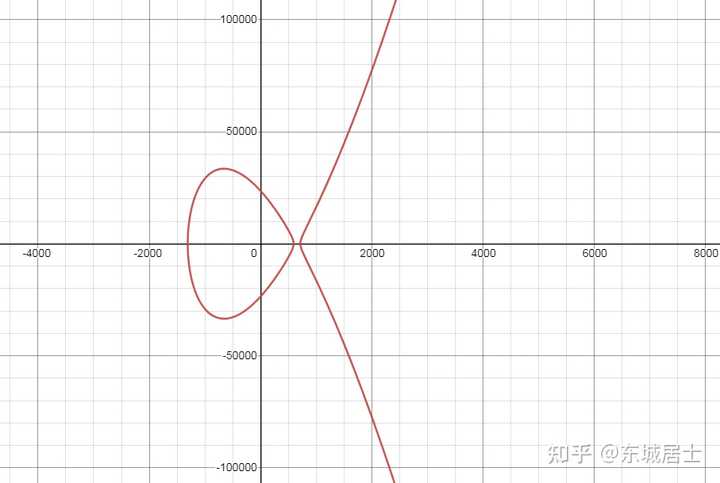
椭圆曲线 Y^2 = X^3 + X^2 ? 1290080X + 556370100
可以验证曲线
~~~~~~V^2=136U^4-1073U^2+1666
上的有理点 (1,-27) 对应椭圆曲线 E 上的有理点
~~~~~~~~~~~~~~P=\left( \frac{9460}{9},\frac{514250}{27} \right).
则由 Nagell-Lutz 定理知 P 为椭圆曲线 E 的无限阶有理点，从而可得 E 上有无穷多个有理点. 椭圆曲线 E 上的每一个有理点，都对应着方程
~~\sum_{i=1}^{6}{A_{i}^{k}}=\sum_{i=1}^{6}{B_{i}^{k}}~~~(k=2,4,6,8,10)
的一组整数解.
如椭圆曲线 E 上的有理点 P 对应着
~~~~~~~~~~~~~~x=1,~~y=3,~~z=1.
从而可得方程
~~\sum_{i=1}^{6}{A_{i}^{k}}=\sum_{i=1}^{6}{B_{i}^{k}}~~~(k=2,4,6,8,10)
的一组整数解
(6,-8,14,12,18,-4),~~(4,-6,18,8,14,-12).
容易看出这是一组平凡解. 为了得到非平凡解，我们取椭圆曲线 E 上的有理点
~~~~~~~~~2P=\left( \frac{163579}{225},-\frac{6090292}{3375} \right).
这个点对应着
~~~~~~~~~U=-\frac{457}{353},~~~V=-\frac{1968867}{124609}.
而这又对应着
x=-101911,~y=346293,~z=78719.
从而可得方程
~~\sum_{i=1}^{6}{A_{i}^{k}}=\sum_{i=1}^{6}{B_{i}^{k}}~~~(k=2,4,6,8,10)
的一组整数解
(1019171,774217,712866,447858,428496,102257),
(1018599,795069,652598,570049,264662,224448).
Chouhdry 和 Wroblewski 用这种方法一共找到了 113 组解，其中较小的 5 组解见下表.

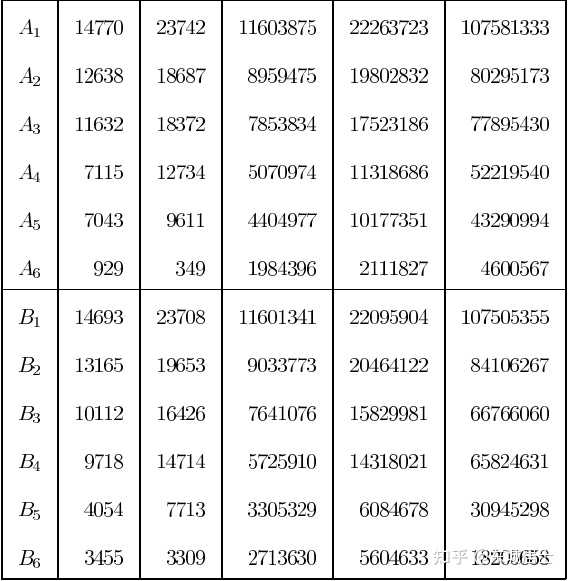
Chouhdry 和 Wroblewski 得到的 5 组较小的解
如由表中的第一组解
(14770,12638,11632,7115,7043,929),
(14693,13165,10112,9718,4054,3455).
可得方程
~~~~~~~~~\sum_{i=1}^{12}{a_{i}^{k}}=\sum_{i=1}^{12}{b_{i}^{k}}~~~~(1\leq k\leq11).
的一组整数解
(\pm14770,\pm12638,\pm11632,\pm7115,\pm7043,\pm929),
(\pm14693,\pm13165,\pm10112,\pm9718,\pm4054,\pm3455).
若这组解的每个数都加 14771 ，则可得方程
~~~~~~~~~\sum_{i=1}^{12}{a_{i}^{k}}=\sum_{i=1}^{12}{b_{i}^{k}}~~~~(1\leq k\leq11).
的一组正整数解
(1,2133,3139,7656,7728,13842,15700,21814,21886,26403,27409,29541),
(78,1606,4659,5053,10717,11316,18226,18825,24489,24883,27936,29464).
用计算机验证结果如下：

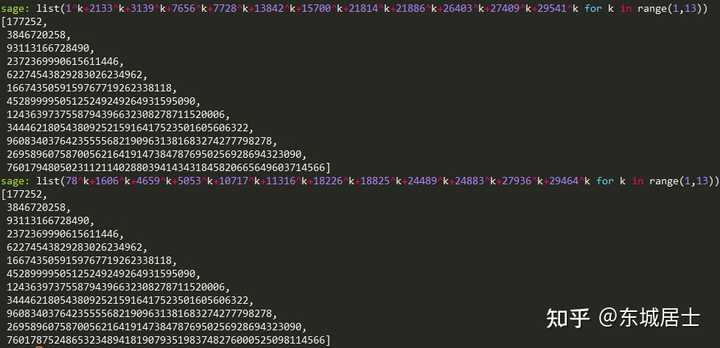
可知确实为方程的解！

说一个众所周知
对于巴塞尔问题（Basel problem）的Euler首个证明，事实上他对这个问题是给出过严谨的证明，但是由于第一个证明实在是太优秀了,只是幂级数同有限的多项式相联系。
已知 sin(x)= \sum_{n=0}^\infty \frac{(-1)^nx^{2n+1}}{(2n+1)!}=x?\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...
从而得 \frac{sin(x)}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\cdots
但是 \frac{sin(x)}{x} 的根集为 x=n\cdot\pi (n=\pm1,\pm2\cdots)
故而可以假定 \frac{sin(x)}{x} =\left( 1-\frac{x}{\pi} \right)\left( 1+\frac{x}{\pi} \right)\left( 1-\frac{x}{2\pi} \right)\left( 1+\frac{x}{2\pi} \right)\left( 1-\frac{x}{3\pi} \right)\left( 1+\frac{x}{3\pi} \right)...=\left( 1-\frac{x^2}{\pi^2} \right)\left( 1-\frac{x^2}{4\pi^2} \right)\left( 1-\frac{x^2}{9\pi^2} \right)\cdots
稍有数学背景的人立刻意识到，咦这个不是《数学分析》里的无穷乘积嘛
\frac{sin(x)}{x} =\prod_{n=1}^{\infty}cos\frac{x}{2^n} 没错就是这个它不过Euler并没有证明这个无穷积，而是百余年后的Weierstrass 的Weierstrass factorization theorem 。
然后Euler对这个无穷乘积的 x^2 项进行研究
-\left( 1-\frac{x^2}{\pi^2} + 1-\frac{x^2}{4\pi^2} +1-\frac{x^2}{9\pi^2} \right)\cdots=-\frac{1}{\pi^2}\sum_{n=1}^{\infty}{\frac{1}{n^2}}
-\frac{1}{6}=-\frac{1}{\pi^2}\sum_{n=1}^{\infty}{\frac{1}{n^2}} 整理一下就是 \sum_{n=1}^{\infty}{\frac{1}{n^2}}=\frac{\pi^2}{6} 不过这个证明过程是有问题的，至少是不严谨的。但是Euler 真神了！
\sum_{n=1}^\infty \frac{1}{n^2} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots=\frac{\pi^2}{6}\approx1.644934 \cdots 这是多么震撼的

在我看来，数学的魅力主要来自于优秀的数学家们可以不断的给人们带来惊喜，将原本杂乱无章的世界解释的井井有条。
拿动力系统来说，Sinai和Kolmogorov发现了一个基本的不变量，熵（entropy），使人们对动力系统的本质有了更深的理解。而对于一般群作用下的动力系统，entropy并不能自然的推广。其中最著名的例子是Ornstein和Weiss在1980年代举出的，他们举出的例子说明如果把entropy的定义简单的推广到自由群作用上，就会出现一个动力系统的因子的熵比原动力系统的熵还大的现象。这个疑惑经过了20多年，终于由Lewis Bowen在2008年左右解决。他对于一般的群作用动力系统定义了一种全新的熵，我们现在称为sofic entropy，这是群作用动力系统的一个基本的不变量，用sofic entropy，我们可以区分很多过去区分不了的动力系统，对于群作用的动力系统也有了崭新的研究角度。
我的PhD导师有一次跟我说，世界之所以这么美，不是因为它原本美，是因为我们的眼睛和大脑把它呈现得很美。数学的美也是一样，主要来自于数学家们对数学深刻的理解和天才的创造，将复杂的现象用简单的语言和公式呈现出来。

[收藏本文] 【下载本文】

自然科学最新文章

海南一村民被眼镜王蛇咬死，多名消防员和村

有哪些不起眼的牢底坐穿兽？

美国耕地面积比中国大，可为什么粮食产量不

如何看待同济大学2024国家科技三大奖颗粒无

加:2024-02-28 16:07:46 更:2024-02-29 11:06:47

股票涨跌实时统计涨停板选股分时图选股跌停板选股 K线图选股成交量选股均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

网站联系: qq:121756557 email:121756557@qq.com 天天财汇