| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 600 个人站一排,每次随机杀掉一个奇数位的人,几号最安全? -> 正文阅读 |
|
|
[时尚穿搭]600 个人站一排,每次随机杀掉一个奇数位的人,几号最安全? |
| [收藏本文] 【下载本文】 |
|
最安全参考两种定义方式: 杀死需要的次数的期望值最大。 成为最后一个被杀死的概率最大。 |
|
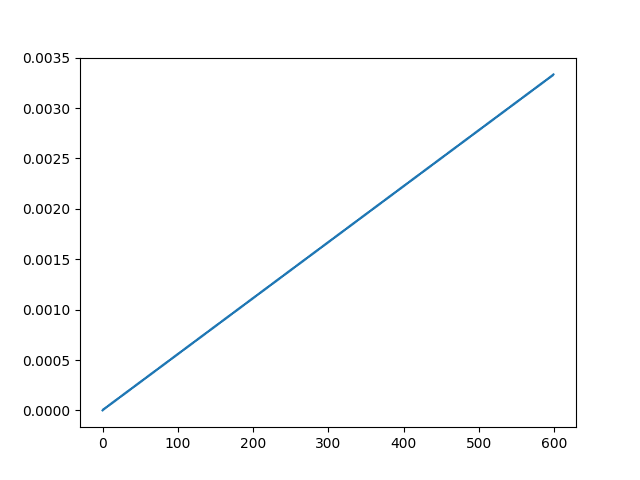
修正之后的结论:存活回合数期望最大的应该是2,但最可能成为最后一个存活的人的是600。 我们来研究M个人杀N次的情况下,每个位置被杀的概率P(k;M,N)。 可以用递推法计算。首先2个人杀一次的情况下,2一定是最好的,P(1;2,1) = 1,P(2;2,1) = 0。M个人杀一次的情况下,偶数被杀概率为0,奇数被杀概率相等:P(2k; M, 1) = 0,P(2k+1; M, 1) = \frac{1}{\lceil\frac{M}{2}\rceil} 考虑M+1个人杀N+1次的情况,则很容易得到: P(2k; M+1, N+1) = \frac{k}{\lceil \frac{M + 1}{2} \rceil} P(2k-1; M, N) + (1-\frac{k}{\lceil \frac{M + 1}{2} \rceil}) P(2k; M, N) P(2k + 1; M+1, N+1) = \frac{1}{\lceil\frac{M + 1}{2}\rceil} + \frac{k}{\lceil \frac{M + 1}{2} \rceil} P(2k; M, N) + (1-\frac{k + 1}{\lceil \frac{M + 1}{2} \rceil}) P(2k+1; M, N) 我们定性分析一下这个式子,无论奇数还是偶数,都从(M,N)的情况中,继承自己和前一项的“阵亡”概率,同时补上自己是奇数(有被杀概率)或者是偶数(无被杀概率)的修正值。k越小,前一项加权越小,后一项加权越大。奇数项有额外的加成。这样,k比较小的情况下,奇数项和偶数项的差异越来越大;而k越大,由于前后两项平均、甚至前项比例超过后项的效果,奇数项和偶数项的差距变得越来越小。 迭代下去的结果大致是一个上下波动然后衰减的样式:1的被杀概率最大,2最小,3又变大但小于1,4又变小但大于2,依次类推。M和N都比较大的时候,靠后位置的奇数位置、偶数位置差异变得很小,因为它们经常相互转换。而1永远是奇数;2只有很小的概率会转换成1。N越大,存活概率的绝对值都变小,但存活概率与前后位置的关系变得更大,2的相对安全优势也越明显。如果考虑最后一个存活的人的比例的话,N很大的情况下,2的优势会很明显。 ==================================================================== 事实证明全凭臆想是不好的……这里忽略了一件事,一开始在2,和最后几轮在2,意义是完全不同的。一开始奇数多,每个奇数被杀概率比较小,而最后几轮被杀概率严重提高,而一开始在2的,很容易就滑到1去了。还是老老实实算一下递推式…… 存活概率: |
|
|
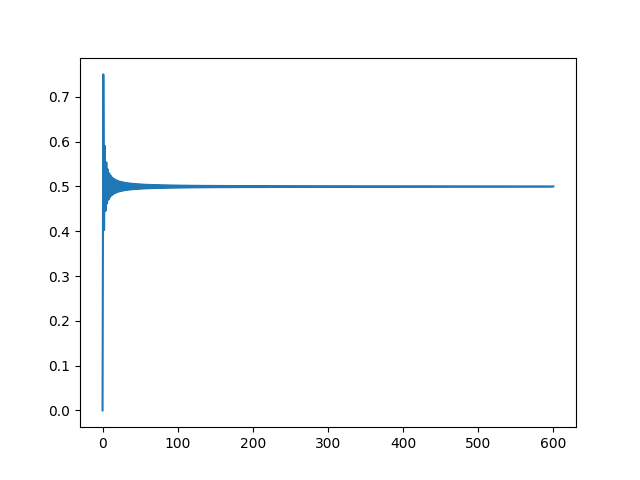
杀至最后一人的存活概率。这也太直了吧! 但其实并不是完美直线,而是奇数偶数一组跳变的,1的存活概率是0,(2,3)的存活概率几乎一样,(4,5)的存活概率几乎一样,依次类推,所以最后存活概率最大的是600,它存活的概率几乎就是1/300。 实际上似乎有P(2k;M,M−1)=P(2k+1;M,M−1)=1−k⌈M2⌉⌈M−12⌉" role="presentation">P(2k;M,M?1)=P(2k+1;M,M?1)=1?k?M2??M?12?P(2k; M, M-1) = P(2k+1; M, M-1) = 1 - \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil} 我们代回去检验一下: P(2k;M+1,M)=k⌈M+12⌉P(2k−1;M,M−1)+(1−k⌈M+12⌉)P(2k;M,M−1)" role="presentation">P(2k;M+1,M)=k?M+12?P(2k?1;M,M?1)+(1?k?M+12?)P(2k;M,M?1)P(2k; M+1, M) = \frac{k}{\lceil \frac{M + 1}{2} \rceil} P(2k-1; M, M - 1) + (1-\frac{k}{\lceil \frac{M + 1}{2} \rceil}) P(2k; M, M - 1) =k⌈M+12⌉(1−k−1⌈M2⌉⌈M−12⌉)+(1−k⌈M+12⌉)(1−k⌈M2⌉⌈M−12⌉)" role="presentation">=k?M+12?(1?k?1?M2??M?12?)+(1?k?M+12?)(1?k?M2??M?12?)= \frac{k}{\lceil \frac{M + 1}{2} \rceil} (1 - \frac{k - 1}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil}) + (1-\frac{k}{\lceil \frac{M + 1}{2} \rceil})(1 - \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil}) =1−k⌈M2⌉⌈M−12⌉+k⌈M2⌉⌈M−12⌉⌈M+12⌉" role="presentation">=1?k?M2??M?12?+k?M2??M?12??M+12?= 1 - \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil} + \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil\lceil \frac{M + 1}{2} \rceil} =1−(⌈M+12⌉−1)k⌈M2⌉⌈M−12⌉⌈M+12⌉" role="presentation">=1?(?M+12??1)k?M2??M?12??M+12?= 1 - \frac{(\lceil \frac{M + 1}{2} \rceil - 1)k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil\lceil \frac{M + 1}{2} \rceil} =1−⌈M−12⌉k⌈M2⌉⌈M−12⌉⌈M+12⌉" role="presentation">=1??M?12?k?M2??M?12??M+12?= 1 - \frac{\lceil \frac{M - 1}{2} \rceil k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil\lceil \frac{M + 1}{2} \rceil} =1−k⌈M2⌉⌈M+12⌉" role="presentation">=1?k?M2??M+12?= 1 - \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M + 1}{2} \rceil} P(2k+1;M+1;M)=1⌈M+12⌉+k⌈M+12⌉P(2k;M,N−1)+(1−k+1⌈M+12⌉)P(2k+1;M,N−1)" role="presentation">P(2k+1;M+1;M)=1?M+12?+k?M+12?P(2k;M,N?1)+(1?k+1?M+12?)P(2k+1;M,N?1)P(2k + 1; M+1; M) = \frac{1}{\lceil\frac{M + 1}{2}\rceil} + \frac{k}{\lceil \frac{M + 1}{2} \rceil} P(2k; M, N-1) + (1-\frac{k + 1}{\lceil \frac{M + 1}{2} \rceil}) P(2k+1; M, N-1) =1⌈M+12⌉+(1−1⌈M+12⌉)(1−k⌈M2⌉⌈M−12⌉)" role="presentation">=1?M+12?+(1?1?M+12?)(1?k?M2??M?12?)= \frac{1}{\lceil\frac{M + 1}{2}\rceil} + (1-\frac{1}{\lceil \frac{M + 1}{2} \rceil}) (1 - \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil}) =1⌈M+12⌉+⌈M−12⌉⌈M+12⌉(⌈M2⌉⌈M−12⌉−k⌈M2⌉⌈M−12⌉)" role="presentation">=1?M+12?+?M?12??M+12?(?M2??M?12??k?M2??M?12?)= \frac{1}{\lceil\frac{M + 1}{2}\rceil} + \frac{\lceil \frac{M - 1}{2} \rceil}{\lceil \frac{M + 1}{2} \rceil}(\frac{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil - k}{\lceil \frac{M}{2} \rceil\lceil \frac{M-1}{2} \rceil}) =1−k⌈M2⌉⌈M+12⌉" role="presentation">=1?k?M2??M+12?= 1 - \frac{k}{\lceil \frac{M}{2} \rceil\lceil \frac{M + 1}{2} \rceil} 这提示我们也许应该用存活概率来表示递推式,改写一下,用Q(k; M, N)来表示存活概率: Q(2k;M+1,N+1)=k⌈M+12⌉Q(2k−1;M,N)+(1−k⌈M+12⌉)Q(2k;M,N)" role="presentation">Q(2k;M+1,N+1)=k?M+12?Q(2k?1;M,N)+(1?k?M+12?)Q(2k;M,N)Q(2k; M+1, N+1) = \frac{k}{\lceil \frac{M + 1}{2} \rceil} Q(2k-1; M, N) + (1-\frac{k}{\lceil \frac{M + 1}{2} \rceil}) Q(2k; M, N) Q(2k+1;M+1,N+1)=k⌈M+12⌉Q(2k;M,N)+(1−k+1⌈M+12⌉)Q(2k+1;M,N)" role="presentation">Q(2k+1;M+1,N+1)=k?M+12?Q(2k;M,N)+(1?k+1?M+12?)Q(2k+1;M,N)Q(2k + 1; M+1, N+1) = \frac{k}{\lceil \frac{M + 1}{2} \rceil} Q(2k; M, N) + (1-\frac{k + 1}{\lceil \frac{M + 1}{2} \rceil}) Q(2k+1; M, N) 的确可以去掉那个常数项,改写成齐次的递推式。 在N不为M-1的时候,得到的结果跟之前的分析基本一致(Q(600,300)): |
|
|
|
|
|
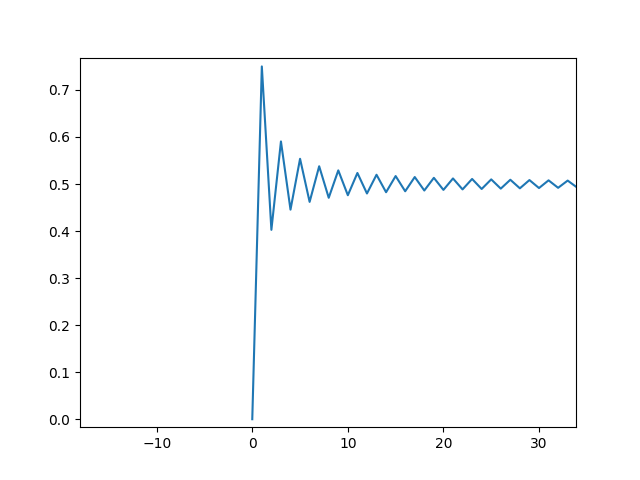
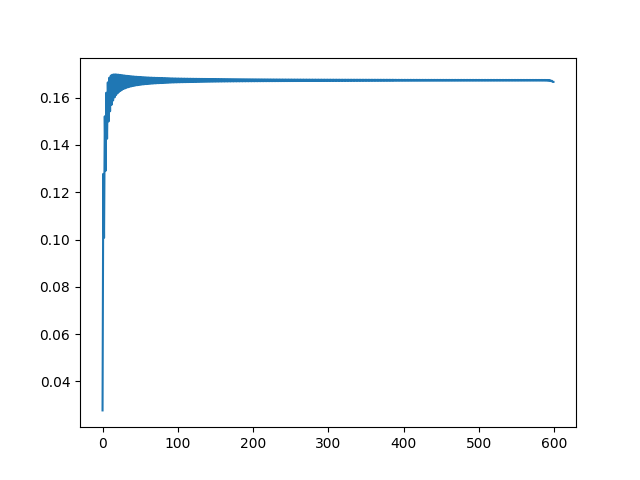
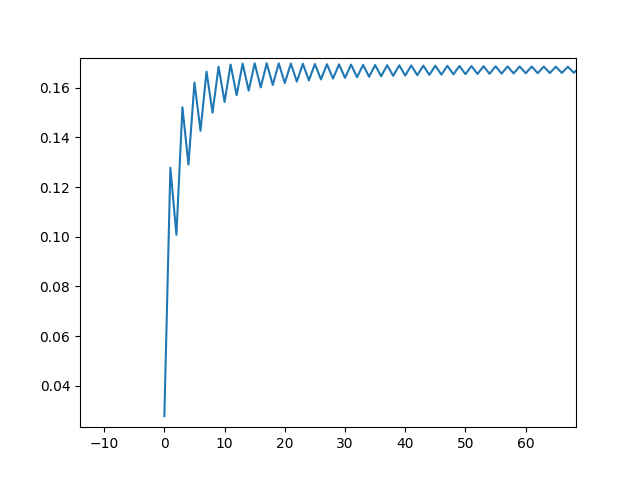
(0实际上是1) 当N增大的时候,这个图也有变化,下图是Q(600,500): |
|
|
|
|
|
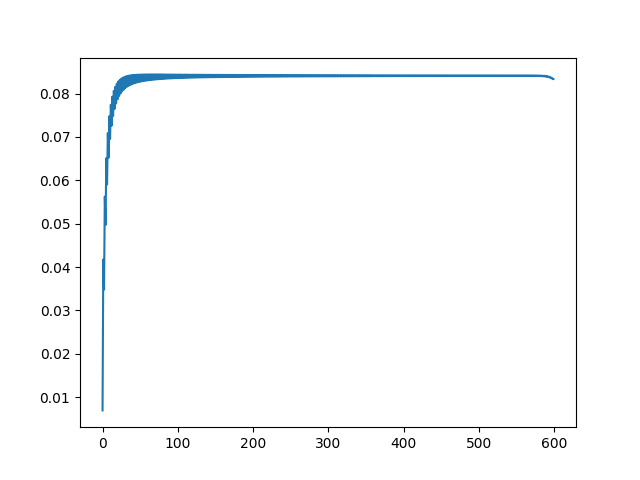
最安全的已经不是2了,而是向后移动,但并没有移动到非常远的地方。 进一步增大的时候(Q(600,550)): |
|
|
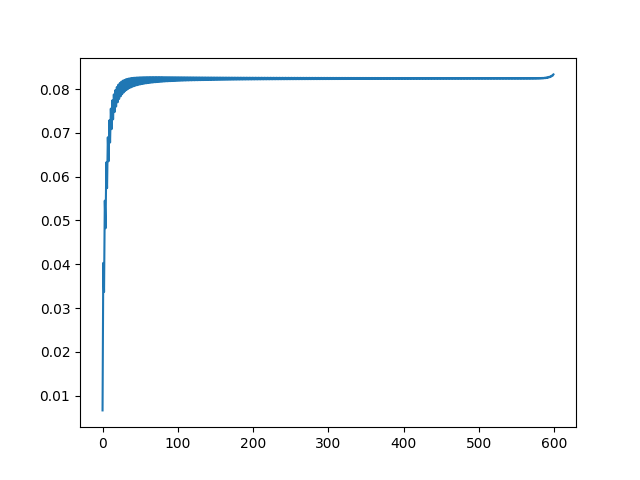
中间大部分地方都变平了,但是注意看那个尾巴,会下降一些,原因不明,但应该不是计算误差,因为随着N增大,这个尾巴变得越来越明显,以至于到599的时候,尾巴变成了整条直线。 更有趣的是这个尾巴的朝向跟N的奇偶性密切相关(Q(600,551)): |
|
|
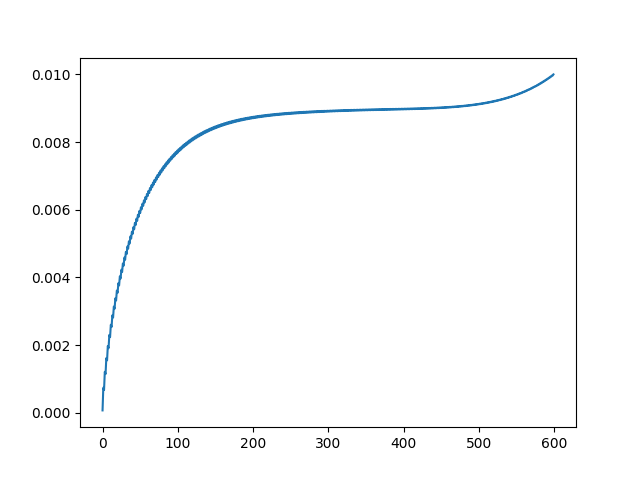
尾巴变成向上了。 N接近于599的时候: Q(600,595) |
|
|
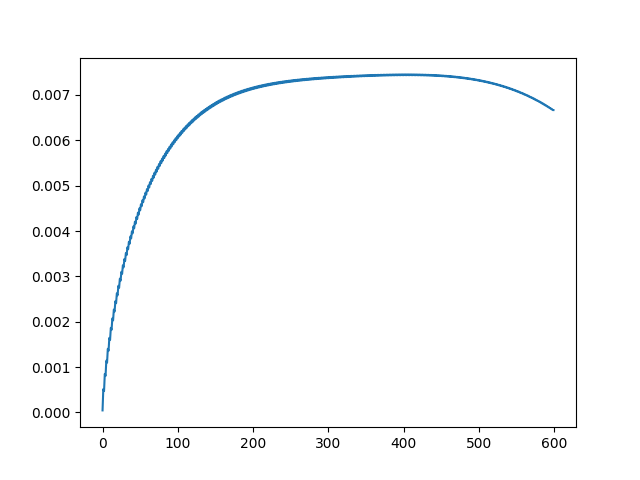
波动越来越不明显,而尾巴越来越明显。 Q(600,596) |
|
|
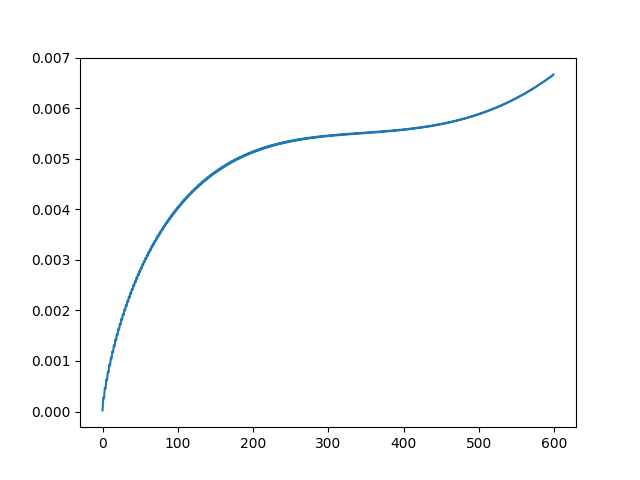
Q(600,597) |
|
|
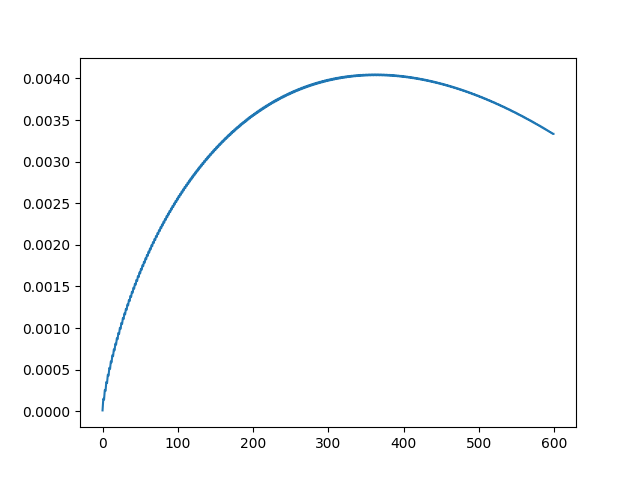
Q(600,598) |
|
|
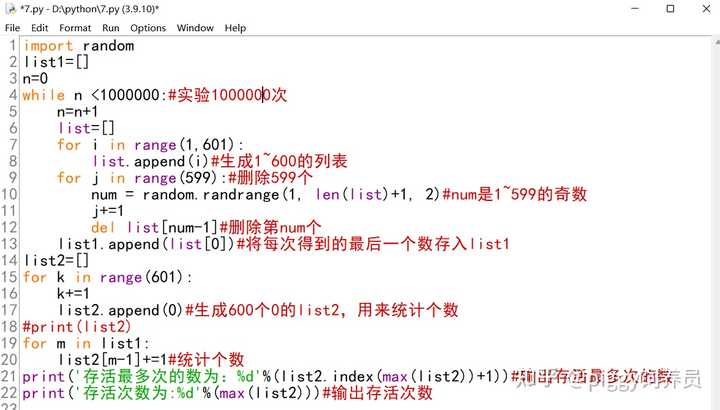
变成了一个这样的奇怪曲线…… 然后599就突变成了直线。只能说,数学真是太奇妙了。 附Python代码: 如果考虑存活回合数的期望值的话,由于N很大的时候存活概率本身就比较小,最后的确应该是2的平均存活回合数比较有优势吧。 解释一下当N比较大的时候,为什么随着N的奇偶性变化,最后一段的概率忽大忽小呢? 因为我们的M = 600是个偶数,当杀奇数人的时候,最后一轮排在最后一个位置的人不会被杀,而杀偶数人时,最后这一轮排在最后一个位置的人可能被杀,而就是这一点点差别导致了差异;杀奇数人时,最后一段很容易成为最后一个人,所以存活概率变大了,在杀599人的时候,甚至这是唯一的存活可能性;杀偶数人时,反而是成为倒数第二个人比较划算,所以最后一小段反而概率下降了。 猜一猜,598那个曲线的极值点在什么位置? 在[0,600]的黄金分割点上。 |
|
|
结案了,一百万次总够了吧 |

|
|
电脑都快跑冒烟了 |
|
这是一个递归问题。 题目所说的情况,我们且称为“600人局”,杀掉一人后,变为“599人局”,以此类推。 我们现在从2人局开始往上推。 2人局:1必死,2存活。存活率是(0,1)。 3人局:有1/2概率杀掉1,留下 [2, 3] 进入2人局,按照2人局的结论,就是2死3活;还有1/2概率杀掉3,留下 [1, 2] 进入2人局,1死2活。这样看,1还是必死,2和3分别有1/2概率存活,存活率是(0,1/2,1/2)。 4人局:有1/2概率进入 [2, 3, 4],2死,3和4各有1/2概率存活(3人局的结论);有1/2的概率进入[1, 2, 4],1死,2和4各有1/2概率存活。最终存活率为(0,1/4,1/4,1/2)。 5人局:各有1/3概率进入 [2, 3, 4, 5]、[1, 2, 4, 5]、[1, 2, 3, 4]。套用4人局的结论,2在第一个情况必死,在后两个情况的存活率各为 1/4,总体存活率为 (1/3)x(0) + (2/3)x(1/4) = 1/6,3的存活率也是1/6,4是 (2/3)x(1/4) + (1/3)x(1/2) = 1/3,5是 (2/3)x(1/2) + (1/3)x0 = 1/3。最终,全体的存活率为(0,1/6,1/6,1/3,1/3)。 6人局:各有1/3概率进入 [2, 3, 4, 5, 6]、[1, 2, 4, 5, 6]、[1, 2, 3, 4, 6]。重复上面的计算过程,全体的存活率为(0,1/9,1/9,2/9,2/9,1/3)。 当然,你可以一直推导到600人局。不过算到这里,已经能看出规律了。我们把存活率改为存活比例来看。 2人局的存活比例是 0:1 3人局 0:1:1 4人局 0:1:1:2 5人局 0:1:1:2:2 6人局 0:1:1:2:2:3 以此类推,600人局的存活比例为 0:1:1:2:2:3:…:299:299:300 600号的存活率最高,为 300/(1+1+2+2+3+…+299+299+300) = 300/90000 = 1/300 剩余人数为奇数时,最后两个人的存活率并列最高;剩余人数为偶数时,最后一个人的存活率最高。 用代数来表示的话,在M人局中求N号选手的存活率 分子是 N//2 分母是 (M//2) * (M//2 + M%2) 注:A//B表示 “A除以B,取整数”;A%B表示 “A除以B,取余数”。 存活率是 (N//2) / [(M//2) * (M//2 + M%2)] 可以试试用这个公式去计算上面列举的2-6人局中各个位置的存活率,会发现结果相符 |
|
一开始凭直觉我选2,因为选2的话,只要1不死,你就不可能死,因为你一直是偶数,而排在队尾的人会不断变化奇偶,一直有死亡的风险... 然后我就写代码模拟了一下,测试了十万次,看几号活下来的次数最多,结果如下: 前面是号码,后面是活下来的次数。 [(597, 359), (576, 355), (598, 354), (586, 352), (587, 348), (573, 347), (578, 347), (600, 346), (560, 337), (565, 337), (585, 335), (589, 335), (583, 334), (554, 333), (564, 333), (595, 333), (577, 332), (580, 332), (596, 332), (592, 331), (599, 325), (563, 324), (568, 324), (591, 324), (562, 323), (574, 322), (546, 321), (550, 319), (551, 318), (579, 318), (567, 317), (581, 316), (584, 316), (588, 316), (557, 315), (558, 315), (522, 314), (570, 314), (566, 313), (532, 312), (548, 312), (582, 312), (547, 311), (524, 310), (525, 310), (552, 310), (555, 310), (514, 309), (559, 309), (541, 308), (507, 307), (571, 306), (515, 305), (504, 304), (527, 304), (517, 302), (538, 302), (509, 301), (518, 301), (526, 301), (553, 301), (544, 300), (542, 299), (561, 299), (520, 298), (569, 298), (536, 297), (572, 297), (492, 296), (543, 296), (516, 295), (471, 294), (497, 294), (590, 294), (594, 294), (510, 293), (528, 293), (530, 293), (549, 292), (593, 292), (485, 291), (511, 291), (470, 290), (534, 290), (540, 290), (512, 289), (496, 286), (529, 286), (513, 285), (539, 285), (556, 285), (535, 283), (483, 281), (490, 281), (506, 281), (508, 281), (533, 281), (489, 279), (457, 278), (521, 278), (545, 278), (450, 277), (479, 277), (519, 277), (523, 277), (449, 276), (495, 276), (503, 275), (537, 275), (438, 273), (494, 273), (475, 272), (531, 272), (491, 271), (502, 271), (481, 270), (501, 270), (476, 269), (477, 269), (575, 269), (484, 267), (493, 267), (417, 264), (478, 264), (432, 263), (458, 263), (498, 263), (499, 263), (452, 262), (482, 262), (460, 261), (466, 261), (486, 261), (505, 261), (454, 260), (473, 259), (440, 258), (469, 258), (443, 257), (468, 257), (451, 256), (488, 256), (409, 255), (447, 255), (422, 251), (465, 251), (436, 250), (442, 250), (385, 249), (474, 249), (480, 249), (403, 248), (406, 248), (429, 248), (472, 248), (424, 247), (448, 247), (456, 247), (462, 246), (467, 246), (384, 245), (386, 245), (416, 245), (464, 245), (431, 244), (453, 243), (500, 243), (401, 242), (463, 242), (415, 241), (445, 241), (420, 240), (414, 239), (411, 238), (444, 238), (461, 238), (412, 237), (427, 237), (446, 237), (455, 237), (399, 236), (433, 235), (435, 234), (392, 232), (423, 232), (425, 232), (459, 232), (372, 231), (419, 231), (434, 231), (387, 229), (437, 229), (404, 228), (421, 228), (487, 228), (428, 227), (439, 227), (375, 226), (398, 226), (405, 226), (391, 225), (441, 225), (389, 223), (396, 223), (377, 222), (383, 222), (366, 220), (430, 220), (347, 219), (350, 217), (341, 216), (364, 216), (382, 216), (395, 216), (407, 216), (408, 216), (357, 215), (380, 215), (390, 214), (332, 213), (367, 213), (368, 211), (410, 211), (370, 210), (374, 210), (324, 209), (426, 208), (314, 207), (358, 207), (376, 206), (381, 205), (413, 205), (361, 204), (397, 203), (349, 202), (379, 202), (402, 202), (400, 200), (343, 199), (353, 199), (362, 198), (316, 197), (371, 197), (290, 196), (356, 196), (360, 195), (373, 195), (393, 195), (388, 194), (394, 194), (418, 194), (328, 192), (345, 192), (333, 191), (344, 191), (378, 191), (325, 190), (289, 189), (327, 189), (335, 189), (340, 189), (352, 189), (354, 189), (355, 189), (319, 186), (322, 186), (326, 186), (334, 186), (329, 185), (348, 185), (287, 184), (338, 184), (369, 183), (309, 181), (320, 181), (321, 181), (301, 180), (330, 180), (346, 180), (365, 180), (311, 179), (315, 179), (268, 178), (293, 178), (363, 178), (331, 177), (272, 176), (298, 175), (342, 175), (339, 173), (302, 172), (305, 172), (359, 170), (303, 169), (308, 169), (318, 169), (288, 168), (295, 168), (274, 167), (312, 167), (286, 166), (299, 166), (336, 166), (292, 165), (310, 164), (313, 164), (351, 163), (256, 162), (294, 162), (232, 161), (276, 160), (306, 160), (291, 159), (317, 158), (337, 158), (262, 157), (278, 157), (283, 156), (300, 156), (304, 156), (323, 154), (264, 153), (270, 152), (275, 152), (296, 152), (265, 151), (282, 151), (277, 150), (307, 149), (273, 148), (279, 148), (238, 147), (263, 147), (237, 146), (261, 145), (281, 144), (297, 144), (244, 143), (255, 143), (247, 142), (248, 142), (249, 142), (267, 142), (218, 141), (280, 141), (254, 140), (266, 140), (271, 139), (284, 139), (191, 138), (240, 138), (258, 138), (211, 136), (241, 136), (253, 136), (239, 135), (235, 133), (246, 133), (245, 132), (213, 131), (242, 131), (257, 130), (190, 129), (217, 129), (250, 129), (260, 129), (269, 128), (285, 128), (231, 127), (233, 127), (197, 126), (220, 126), (223, 125), (224, 125), (226, 125), (228, 124), (252, 124), (221, 123), (207, 122), (215, 122), (216, 121), (227, 121), (210, 120), (193, 119), (225, 119), (230, 119), (251, 119), (234, 118), (236, 118), (195, 117), (208, 117), (196, 116), (199, 116), (259, 116), (219, 115), (229, 114), (243, 113), (203, 112), (200, 111), (212, 110), (222, 108), (163, 105), (204, 105), (175, 104), (184, 104), (202, 104), (156, 102), (189, 102), (206, 102), (209, 102), (214, 102), (188, 101), (192, 99), (194, 99), (150, 98), (177, 98), (167, 97), (181, 97), (183, 95), (186, 95), (140, 94), (168, 93), (187, 93), (205, 93), (176, 92), (173, 91), (160, 90), (169, 90), (171, 90), (178, 90), (201, 90), (172, 89), (174, 89), (198, 89), (185, 88), (164, 87), (182, 87), (158, 86), (141, 85), (149, 85), (134, 83), (161, 83), (179, 83), (127, 82), (180, 82), (157, 81), (159, 81), (165, 81), (170, 81), (145, 80), (147, 80), (162, 80), (139, 79), (155, 79), (115, 78), (142, 78), (130, 77), (152, 76), (126, 75), (131, 75), (137, 75), (146, 75), (122, 74), (133, 74), (148, 73), (154, 73), (153, 72), (151, 71), (166, 71), (120, 70), (129, 70), (118, 69), (135, 69), (119, 68), (143, 67), (144, 67), (109, 66), (124, 66), (132, 66), (138, 66), (114, 65), (110, 64), (111, 63), (113, 63), (116, 63), (136, 62), (104, 61), (100, 60), (91, 59), (98, 59), (103, 59), (121, 59), (123, 59), (128, 58), (107, 57), (112, 57), (95, 56), (105, 56), (125, 56), (97, 54), (78, 53), (99, 53), (89, 52), (88, 51), (94, 51), (96, 51), (106, 49), (117, 49), (79, 48), (108, 47), (102, 46), (69, 45), (73, 45), (80, 43), (85, 43), (86, 43), (92, 43), (59, 41), (81, 41), (74, 40), (93, 40), (101, 40), (72, 39), (75, 39), (84, 39), (87, 39), (90, 39), (58, 38), (64, 38), (70, 38), (51, 37), (68, 37), (76, 36), (82, 36), (48, 35), (65, 35), (41, 34), (40, 33), (56, 33), (61, 33), (49, 32), (62, 32), (71, 32), (83, 32), (46, 31), (67, 31), (77, 31), (55, 30), (60, 30), (52, 29), (63, 29), (57, 28), (45, 27), (47, 27), (50, 27), (54, 27), (66, 27), (53, 25), (39, 23), (44, 23), (37, 22), (38, 22), (33, 21), (34, 21), (36, 21), (42, 21), (43, 21), (27, 18), (28, 18), (22, 17), (26, 16), (35, 16), (24, 15), (30, 14), (31, 14), (18, 13), (20, 13), (16, 12), (17, 12), (32, 12), (19, 11), (29, 11), (15, 10), (11, 9), (25, 9), (8, 7), (12, 7), (14, 7), (21, 7), (23, 7), (13, 6), (7, 5), (9, 5), (10, 4), (6, 3), (5, 2), (3, 1), (4, 1), (1, 0), (2, 0)] 可以看出有点反直觉,号码越大活下来的次数越多,2反而一次都没有幸存过...讲道理2应该是有机会的,当且仅当1号和2号是最后两个幸运儿的情况下,2号能活到最后;只要前面1死了,2必死,因为2号变成奇数了,且永远是奇数... 然后我又换了一个思路,不是找出最后一个活下来的人,而是找每个位置被干掉时的平均轮次,期望最大的位置就是在"杀死X人后就停止游戏"模式下,最该选的位置。这种情况下,2才是最优解,10W次平均下来可以活334轮。 [(2, 334.85462), (4, 324.15324), (6, 318.03607), (8, 314.53773), (10, 312.15009), (12, 310.24678), (14, 309.83584), (16, 308.15376), (20, 308.08513), (24, 306.97496), (22, 306.91657), (18, 306.56934), (26, 305.27079), (34, 305.20893), (30, 305.12727), (28, 304.86014), (38, 304.68987), (36, 304.61869), (40, 304.20346), (60, 304.09304), (72, 304.05492), (46, 304.00212), (48, 303.77202), (56, 303.73308), (32, 303.70517), (68, 303.44412), (44, 303.40699), (76, 303.28368), (54, 303.27495), (58, 303.27351), (136, 303.22399), (52, 303.18093), (64, 303.16217), (92, 303.15471), (88, 303.12217), (94, 302.9876), (106, 302.94762), (74, 302.91037), (50, 302.88765), (356, 302.88328), (42, 302.83717), (102, 302.83614), (62, 302.81658), (124, 302.79908), (208, 302.6461), (100, 302.63596), (80, 302.58573), (146, 302.53383), (128, 302.40043), (182, 302.37766), (66, 302.37435), (340, 302.34032), (84, 302.31475), (78, 302.31181), (206, 302.29824), (70, 302.2765), (150, 302.26535), (108, 302.25733), (236, 302.2203), (116, 302.20057), (188, 302.185), (186, 302.17129), (126, 302.16539), (272, 302.14484), (408, 302.12267), (138, 302.0991), (282, 302.09234), (104, 302.08849), (202, 302.08609), (130, 302.05452), (454, 302.04717), (230, 302.03887), (260, 302.0247), (196, 302.01771), (348, 302.00776), (270, 302.00579), (110, 301.9752), (496, 301.9628), (90, 301.96193), (120, 301.95368), (192, 301.93925), (244, 301.93474), (468, 301.93351), (597, 301.92656), (536, 301.90763), (564, 301.90078), (416, 301.8996), (228, 301.89672), (118, 301.86935), (98, 301.86074), (220, 301.85789), (504, 301.84736), (506, 301.84461), (164, 301.83767), (82, 301.83346), (592, 301.81593), (172, 301.77913), (112, 301.77641), (160, 301.77316), (166, 301.74413), (414, 301.72875), (144, 301.72661), (156, 301.70811), (132, 301.70281), (86, 301.68918), (96, 301.68302), (342, 301.67392), (530, 301.67366), (224, 301.66795), (404, 301.66377), (152, 301.65855), (218, 301.65), (190, 301.64822), (378, 301.64469), (440, 301.64003), (276, 301.61927), (533, 301.61603), (238, 301.61226), (392, 301.59841), (596, 301.57546), (168, 301.57143), (546, 301.56303), (538, 301.55457), (248, 301.55388), (410, 301.55265), (411, 301.55163), (444, 301.53787), (364, 301.52839), (178, 301.52693), (302, 301.52463), (520, 301.52462), (290, 301.52014), (266, 301.50517), (434, 301.50079), (354, 301.49918), (422, 301.46459), (114, 301.46379), (540, 301.45644), (344, 301.45233), (306, 301.44755), (194, 301.44695), (162, 301.44612), (268, 301.44602), (365, 301.43923), (586, 301.43489), (517, 301.43298), (300, 301.43164), (296, 301.42878), (358, 301.42858), (148, 301.42713), (544, 301.4258), (522, 301.42288), (559, 301.41682), (284, 301.41189), (226, 301.41026), (245, 301.40577), (170, 301.40057), (502, 301.39821), (255, 301.3975), (396, 301.38399), (332, 301.37851), (395, 301.37768), (330, 301.36072), (334, 301.35544), (232, 301.34294), (320, 301.34237), (280, 301.34097), (198, 301.33406), (254, 301.3305), (294, 301.32553), (122, 301.31871), (438, 301.31805), (584, 301.31456), (242, 301.31203), (355, 301.30953), (516, 301.3093), (557, 301.30846), (214, 301.30454), (560, 301.30396), (367, 301.29951), (316, 301.29472), (451, 301.29425), (570, 301.29393), (500, 301.29097), (420, 301.28634), (590, 301.28286), (368, 301.27778), (324, 301.27618), (328, 301.27546), (574, 301.26491), (140, 301.25926), (134, 301.2452), (292, 301.23012), (336, 301.22657), (585, 301.2259), (389, 301.21997), (382, 301.21696), (154, 301.2139), (484, 301.21227), (448, 301.20634), (158, 301.19844), (258, 301.18464), (200, 301.18353), (209, 301.18135), (402, 301.18134), (431, 301.18078), (413, 301.1788), (433, 301.17544), (400, 301.17209), (541, 301.15425), (318, 301.154), (418, 301.15282), (486, 301.15154), (531, 301.14597), (216, 301.13614), (554, 301.13358), (142, 301.12922), (321, 301.12583), (212, 301.11879), (390, 301.10947), (436, 301.10221), (511, 301.10068), (494, 301.09707), (250, 301.09331), (518, 301.08564), (534, 301.08267), (361, 301.08264), (478, 301.08014), (394, 301.07468), (370, 301.06988), (460, 301.06917), (210, 301.06875), (376, 301.06304), (308, 301.05279), (446, 301.05051), (333, 301.04586), (412, 301.03631), (598, 301.03513), (563, 301.03156), (476, 301.02515), (338, 301.02069), (437, 301.01551), (293, 301.01252), (526, 301.00239), (452, 300.9889), (319, 300.98299), (491, 300.97416), (543, 300.96583), (213, 300.95534), (426, 300.95481), (524, 300.95458), (514, 300.94796), (331, 300.94793), (277, 300.94549), (532, 300.943), (415, 300.93183), (492, 300.92734), (303, 300.92573), (222, 300.91827), (582, 300.91764), (589, 300.91628), (346, 300.91307), (398, 300.90946), (561, 300.90728), (456, 300.90014), (473, 300.8869), (269, 300.87927), (594, 300.87904), (366, 300.86993), (278, 300.8503), (385, 300.85025), (499, 300.84888), (204, 300.84674), (295, 300.84209), (581, 300.84142), (335, 300.84045), (240, 300.83815), (443, 300.83061), (191, 300.82292), (469, 300.81836), (479, 300.80903), (464, 300.79993), (472, 300.7917), (264, 300.78885), (322, 300.77927), (428, 300.77142), (483, 300.76892), (545, 300.76889), (474, 300.76517), (558, 300.76212), (314, 300.76016), (509, 300.75938), (515, 300.75781), (176, 300.75518), (271, 300.74916), (482, 300.74316), (508, 300.73768), (566, 300.73678), (234, 300.73599), (391, 300.73318), (562, 300.73216), (591, 300.73121), (362, 300.72655), (384, 300.72311), (576, 300.71459), (430, 300.71153), (305, 300.71115), (184, 300.70853), (593, 300.70736), (447, 300.69003), (288, 300.68323), (573, 300.68065), (381, 300.67603), (547, 300.67531), (449, 300.67492), (231, 300.66485), (363, 300.65597), (180, 300.65275), (461, 300.65101), (357, 300.64421), (553, 300.63929), (374, 300.63756), (252, 300.6323), (372, 300.63123), (439, 300.62922), (599, 300.6264), (588, 300.62502), (343, 300.62028), (466, 300.61701), (253, 300.61201), (442, 300.60987), (583, 300.60926), (195, 300.6068), (137, 300.60063), (326, 300.5997), (291, 300.58589), (345, 300.58361), (174, 300.58266), (380, 300.57932), (388, 300.57581), (155, 300.57217), (490, 300.56931), (550, 300.56738), (256, 300.56594), (595, 300.55435), (298, 300.55192), (251, 300.54332), (279, 300.53939), (350, 300.53105), (397, 300.52598), (568, 300.51707), (327, 300.51672), (221, 300.50989), (312, 300.50501), (481, 300.50204), (246, 300.49963), (470, 300.49424), (274, 300.49282), (175, 300.49146), (493, 300.48546), (262, 300.48466), (432, 300.48236), (580, 300.48222), (425, 300.47463), (498, 300.47326), (205, 300.46869), (406, 300.4636), (552, 300.46066), (463, 300.45809), (459, 300.45588), (556, 300.4549), (488, 300.45307), (471, 300.45128), (360, 300.44997), (199, 300.44032), (371, 300.43315), (310, 300.43292), (485, 300.42953), (261, 300.42819), (197, 300.42151), (373, 300.41495), (229, 300.41198), (549, 300.41091), (179, 300.40888), (424, 300.40664), (267, 300.40607), (501, 300.39616), (419, 300.39156), (505, 300.39052), (578, 300.38601), (352, 300.3855), (457, 300.38335), (525, 300.37539), (542, 300.37402), (587, 300.36838), (551, 300.36684), (219, 300.35185), (329, 300.34586), (287, 300.31599), (393, 300.31475), (572, 300.30156), (503, 300.29912), (462, 300.29822), (225, 300.29569), (401, 300.29498), (453, 300.28758), (286, 300.28053), (565, 300.27658), (487, 300.27087), (510, 300.26524), (215, 300.25942), (187, 300.24968), (325, 300.24773), (407, 300.24371), (455, 300.24088), (309, 300.24075), (435, 300.2252), (512, 300.21649), (480, 300.20573), (121, 300.20046), (263, 300.19342), (353, 300.17889), (281, 300.17533), (313, 300.16192), (337, 300.1587), (301, 300.15462), (528, 300.14869), (421, 300.14814), (257, 300.14513), (265, 300.14151), (445, 300.13972), (507, 300.12832), (185, 300.12465), (495, 300.12329), (579, 300.12283), (529, 300.11603), (386, 300.11102), (151, 300.10925), (147, 300.109), (283, 300.10339), (387, 300.09651), (519, 300.09216), (243, 300.08065), (441, 300.07654), (539, 300.07124), (304, 300.07028), (349, 300.06374), (317, 300.06314), (429, 300.06219), (383, 300.05543), (289, 300.05132), (307, 300.04174), (341, 300.03723), (239, 300.03528), (569, 300.03361), (351, 300.02632), (521, 300.02154), (417, 300.01192), (87, 300.00977), (233, 300.00346), (475, 300.00001), (297, 299.99073), (207, 299.98205), (275, 299.97973), (299, 299.97962), (227, 299.97895), (241, 299.9688), (167, 299.96139), (458, 299.96044), (399, 299.95369), (323, 299.94672), (489, 299.94414), (477, 299.93875), (427, 299.92628), (101, 299.91787), (359, 299.91516), (403, 299.90618), (347, 299.90604), (377, 299.90005), (467, 299.88917), (450, 299.8821), (223, 299.88204), (193, 299.86918), (513, 299.86296), (177, 299.86112), (211, 299.84474), (135, 299.8035), (339, 299.79921), (125, 299.78395), (235, 299.77181), (117, 299.75825), (75, 299.75066), (247, 299.73311), (237, 299.72333), (217, 299.72253), (311, 299.72026), (315, 299.71387), (83, 299.70629), (405, 299.70574), (119, 299.69708), (107, 299.67938), (123, 299.67543), (523, 299.67115), (143, 299.66293), (165, 299.65608), (369, 299.64671), (273, 299.64108), (548, 299.63931), (577, 299.63193), (555, 299.62696), (465, 299.62355), (127, 299.60852), (189, 299.5903), (169, 299.58894), (171, 299.58804), (129, 299.58694), (423, 299.57174), (153, 299.55087), (379, 299.52913), (375, 299.51333), (535, 299.49967), (99, 299.49609), (259, 299.4762), (575, 299.46397), (133, 299.43983), (163, 299.43769), (97, 299.40723), (109, 299.38855), (79, 299.38415), (113, 299.3819), (409, 299.36965), (161, 299.36586), (103, 299.353), (139, 299.35158), (149, 299.34188), (600, 299.31958), (567, 299.3134), (571, 299.30483), (105, 299.2486), (203, 299.23775), (537, 299.22636), (159, 299.22043), (115, 299.20518), (173, 299.2027), (77, 299.20109), (181, 299.1776), (497, 299.12781), (131, 299.10014), (145, 299.03574), (285, 298.96359), (201, 298.92008), (73, 298.91003), (157, 298.88791), (249, 298.86193), (51, 298.82815), (85, 298.80862), (95, 298.78778), (141, 298.73618), (111, 298.67207), (65, 298.66168), (81, 298.62885), (63, 298.59343), (91, 298.5899), (71, 298.51837), (527, 298.48054), (183, 298.38007), (55, 298.37794), (69, 298.35309), (67, 298.34512), (61, 298.13855), (93, 298.12835), (57, 297.92559), (47, 297.89605), (59, 297.84499), (89, 297.59511), (41, 297.59318), (45, 297.30668), (49, 297.28242), (53, 296.87487), (43, 296.86956), (39, 296.25656), (37, 296.21923), (33, 295.94278), (31, 295.75378), (29, 295.58077), (35, 295.33364), (25, 295.22599), (27, 294.75609), (23, 294.59502), (19, 293.31695), (21, 292.99069), (17, 291.126), (13, 290.13547), (15, 289.9777), (11, 286.66999), (9, 283.27233), (7, 278.32448), (5, 270.91142), (3, 253.54469), (1, 201.54989)] |
|
看大家讨论的热火朝天,申明一个自己的观点吧: 因为这是只有一个人幸存的游戏,所以我认为安全的定义只有一个,就是活到最后。这也是为什么我只跑了这一个程序。 试想一个极端情况:即使一个人在一局游戏里活的时间很长,但他仍然必死,那还叫安全嘛? 或者问下自己,让你站2号或者600号,你选哪个? =====更新前内容===== 简单写了个程序,执行了测试一百万次,记录每次最后存活的人的编号,一百万次后计数最多的编号即为最安全编号。 结果如图: |

|
|
|
|
谢邀?~? 按照题主的描述,这个问题分为两问: 两问的答案分别为600号和2号 一、简单的数据打表以及初步分析&答案给出 (1)活到最后一个的那个人,几号概率最大 反对有好多人以如下原因说是2号:除非1号死了,否则2号不会死——但是1号必死无疑,之后2号就成了1号,于是2号能活下来,当且仅当1号能活到“决赛”,这个概率是很小的。 反对有好多人纯“臆断”512号,或是“中间某个号”,“偶数比奇数安全”之类的答案,其实只要前面某个人一死,后面的奇偶性就会全部改变,并且初期死亡概率其实很小(平均下来每个人会有99%+的最终死掉,而初期那几轮那怕一直是奇数也只占百分之几的概率,并不足以产生什么影响),所以初始状态是奇数或是偶数并不会对这个问题产生本质性的影响。 对于“这就一道数学题,那些mark了去写代码的是傻逼么?”的回答,我想文明用语。对于一眼看不出答案的问题,编程猜出答案后数学验证是最为严谨的做法。最主要的,这种方法省时间。此类题只要知道结果了,用数学归纳法分分钟就证毕。 编程结果是:越往后存活概率越大 1<2=3<4=5<6=7...以此类推,并且1,3,5,7...它们存活的概率是以0为首项的等差数列 下面是600个人时的概率打表(因为表太长了,所以只打了表头和表尾 怀疑结论正确性的可以拿n比较小的时候手算验证(比如n=2,3之类的 |

|
|
|

|
|
猜出了结论时候对n用数学归纳法不难从数学层面证明。 (2)活的轮数的数学期望,谁最大 如诸位所愿,这次变成了2号,但是领先优势并没有臆想里那么霸道。并且除了位置靠前的几个倒霉蛋存活期望值不太稳定之外,号大的朋友几乎都能期望活300轮左右(其实除了1号比较倒霉平均少活100轮意外,其他人都是“差不多”平均活300轮,只不过2号能稍微多活微不足道的几轮罢了) |

|
|
|

|
|
至于这一问的数学解释应该蛮难给的,通项公式都未必能很简单的写出来。 二、深入分析以及评论区“答疑” 1.对于上述规律的数学证明 成为“唯一幸存者”的概率 的 等差数列规律(并且很容易分奇偶给出通项公式活的轮数的数学期望值:奇数位递增,且趋近于总轮数的1/2;偶数位递减,且趋近于总轮数的1/2;1号大约是总轮数的1/3,2号大约是总轮数的5/9...(这里甚至可以给出任何一位的期望值是总轮数的百分之多少,用到一点高中组合知识即可证明) 上述结论的证明极其简单,且毫无意义。故略 (有兴趣的看官可以用数学归纳法自行证明,用到知识不超过高中课本范围) 2.“怎么模拟随机过程?不是伪随机吗?” 知道计算机是“伪随机”是好的,但是你还应该知道取time作为seed之后就无限趋近于真随机了(如果你能精确到毫秒按鼠标的话它依然是伪随机,否则就是真的)这里并没有模拟随机过程,只是用到了一点高中数列知识来递推(原理和排名第二的答案是一样的,就不详述了) 3.“请问具体的代码可以分享一下吗?” 实在抱歉。因为搞数学竞赛遍地写ijk的缘故,循环控制变量用的满地ijk,美观性不忍直视,所以就不分享了。关心算法的朋友可以去学习其他的答案分享的代码,大家的算法都是几乎一样的 4.“没给方差不幸福” 因为我并没有模拟随机,所以方差数据是给不出来的但是理论推导,应该是越往前方差越小,越往后方差越大(只是大致趋势,有没有2号=3号,或是等差数列等规律暂未知) 5.“不理解为什么活的轮数最多的人反而最后活下来的几率倒数第二……难道最后活下来的人不是活的轮数最多的吗?” 因为2号位的方差小啊你可以理解成:活到最后一个是“变成千万富翁”,活多少轮就是手里有多少钱。2号位是办理财,600号位是买彩票。那么2号位平均能拿到的钱自然比600号位多,但是他却几乎没有可能变成千万富翁,相比之下600号位还是有一些机会的。 |
|
看了一圈,懂了 2号平均最长命,因为一号不死它就安全,但是一号一死,自己就成了一号,每轮都要抽签,死的飞快。也就是两条命,但闪避清零。 600号最可能活到最后,因为它是最后一个,只要前面死人了就会改变奇偶性,在奇数号的时候没死下一轮就是安全的。也就是带50%额外闪避 总结:如果这是场必败的Boos战,二号就是躲在主T背后的奶妈,600号就是混在人堆里的盗贼。 既然是必败,那剧情十有八九是这样的,一分钟死个人,300分钟,主T咯屁了,350分钟,奶妈咯屁了,接着大家各凭本事,最后盗贼隐身瑟瑟发抖。 |
|
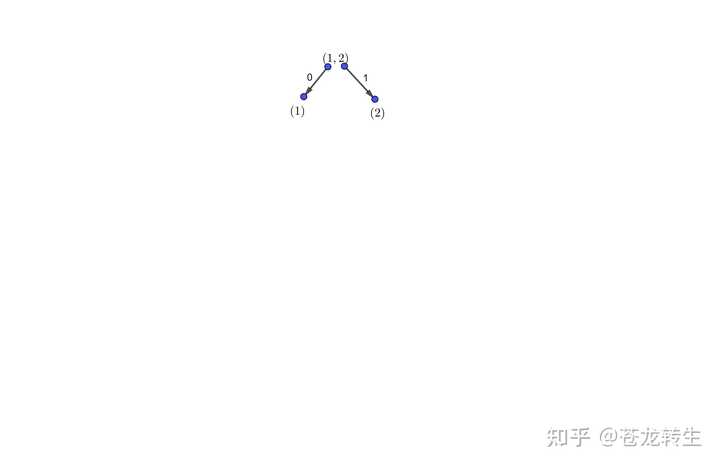
谢邀。 将排成一排的600个人按1到600编号。由题目可知,剩余1人时,共进行了599轮筛选,进行到倒数第一轮时,也就是只剩2个人时,共进行了598轮筛选。下面先看几种情况。 一、暴力计算几种特殊情况1.1、1号最后留下的概率 显然1号最后留下的概率为0。记 p_1=0 1.2、2号最后留下的概率 2号最后能否留下来,取决于1号是否能留到倒数第一轮。也就是倒数第一轮的两人是1号和2号,则2号最后留下来。1号能留到倒数第一轮的概率为: p(1号留到倒数第一轮)=\frac{299}{300}\times\frac{299}{300}\times\frac{298}{299}\times\frac{298}{299}\times……\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{300^2} 因此2号最后留下来的概率为: p_2=p(2号最后留下来)=p(1号留到倒数第一轮)=\frac{299}{300}\times\frac{299}{300}\times\frac{298}{299}\times\frac{298}{299}\times……\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{300^2} 1.3、3号最后留下的概率 3号最后能否留下来,取决于1号或2号能否留到倒数第一轮,也就是倒数第一轮的两人是1号和3号,或者是2号和3号。又因为若1号能留到倒数第一轮,则2号必定能留到倒数第一轮。因此若最后3号留下来,倒数第一轮时只有可能是2号和3号。倒数第一轮是2号和3号的概率为: p(倒数第一轮是2号和3号)=\frac{299}{300}\times\frac{299}{300}\times\frac{298}{299}\times\frac{298}{299}……\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{300^2} 因此: p_3=p(倒数第一轮是2号和3号)=\frac{299}{300}\times\frac{299}{300}\times\frac{298}{299}\times\frac{298}{299}……\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{300^2} 1.4、600号最后留下的概率 600号只需要在前598轮筛选中都没有被选中最后即可留下来,概率为: p_{600}=p(600号最后留下来)=\frac{300}{300}\times\frac{299}{300}\times\frac{299}{299}\times\frac{298}{299}\times\frac{298}{298}\times\frac{297}{298}\times……\times\frac{2}{2}\times\frac{1}{2}=\frac{300!299!}{300!300!}=\frac{1}{300} 1.5、599号最后留下的概率 599号满足以下条件才能在最后留下:在前598轮筛选中都没有被选中,并且600号在前598轮被选中。因此筛选过程为前598轮中有一轮选中600号,597轮选中1到598号中的597人。因此概率为: p_{599}=p(599号最后留下来)=C_{299}^{1}\frac{299!299!}{\left( 300\times299\times298\times……\times2\right)\left( 300\times299\times298\times……\times2\right)}=\frac{299}{300^2} 1.6、598号最后留下的概率 598号满足以下条件才能在最后留下:在前598轮筛选中都没有被选中,并且600号和599号在前598轮被选中。因此筛选过程为前598轮中有两轮选中600号和599号,596轮选中1到597号中的596人。因此概率为: p_{598}=p(598号最后留下来)=\left( 2-1+4-1+6-1+……+598-1 \right)\times\frac{1}{300}\times\frac{1}{300}\times\frac{1}{299}=\frac{299}{300^2} 1.7、597号最后留下的概率 597号满足以下条件才能在最后留下:在前598轮筛选中都没有被选中,并且600号、599号和598号在前598轮被选中。因此筛选过程为前598轮中有三轮选中600号、599号和598号,595轮选中1到596号中的595人。因此概率为: p_{597}=p(597号最后留下来)=\\\left\{ \left[ 1\times2+2 \right]+\left[ \left( 3+1 \right)\times2+\left( 4+2 \right) \right] +\left[ \left( 5+3+1 \right)\times2+\left( 6+4+2 \right) \right]+……+\\\left[ \left( 595+593+……+1 \right)\times2+\left( 596+594+……+2 \right) \right]\right\}\frac{298!298!}{300!300!}\\=2\left[ \left( 1^2+2^2+3^2+……+ 298^2\right)+\left( 1+3+6+10+……+\frac{299\times298}{2} \right) \right]\frac{298!298!}{300!300!}\\=2\left[ \frac{298\times299\times300}{6}+\frac{298\times299\times597}{6} \right]\frac{298!298!}{300!300!}=\frac{298}{300^2} 1.8、结论 经过暴力计算,得出 p_1:p_2:p_3:p_{597}:p_{598}:p_{599}:p_{600}=0:\frac{1}{300^2}:\frac{1}{300^2}:\frac{298}{300^2}:\frac{299}{300^2}:\frac{299}{300^2}:\frac{300}{300^2}=0:1:1:298:299:299:300 至此,可以猜测600号最后留下来的概率最大。然而还是没有得出每个人最后留下来的概率的通项公式。 二、参加游戏的人数从2到5的情况2.1、2人参加游戏 游戏过程如下图所示。 \left( 1,2 \right) 表示开始时的人员。 \left( 1 \right) 和 \left( 2 \right) 表示经过一轮筛选后剩下的人员。 0 和 1 分别表示经过这一轮筛选后人员组成的概率。即\left( 1,2 \right)一轮筛选后留下\left( 1 \right)的概率为0,即\left( 1,2 \right)一轮筛选后留下\left( 2 \right)的概率为1。 |
|
|
容易知道:p_1:p_2=0:1 2.2、3人参加游戏 游戏过程如下图: |

|
|
容易知道: p_1:p_2:p_3=0:\frac{1}{2}:\frac{1}{2}=0:1:1 2.3、4人参加游戏 采用与2人和3人参加游戏时的相同算法,容易验证: p_1:p_2:p_3:p_4=0:\frac{1}{4}:\frac{1}{4}:\frac{1}{2}=0:1:1:2 2.4、5人参加游戏 采用与2人、3人和4人参加游戏时的相同算法,容易验证: p_1:p_2:p_3:p_4:p_5=0:\frac{1}{6}:\frac{1}{6}:\frac{1}{3}:\frac{1}{3}=0:1:1:2:2 2.5、猜测 根据2、3、4、5人参加游戏时最后留下人员的概率以及一中的几种情况,可以猜测有下述规律: 设p_1:p_2:……:p_{2l}:p_{2l+1}:……:p_{2k}:p_{2k+1}\\=0:\frac{1}{\left( k \right)\left( k+1 \right)}:……:\frac{l}{\left( k \right)\left( k+1 \right)}:\frac{l}{\left( k \right)\left( k+1 \right)}:……\frac{k}{\left( k \right)\left( k+1 \right)}:\frac{k}{\left( k \right)\left( k+1 \right)} p_1:p_2:……:p_{2l}:p_{2l+1}:……:p_{2k}\\=0:\frac{1}{k^2}:……:\frac{l}{k^2}:\frac{l}{k^2}:……:\frac{k}{k^2} 三、使用数学归纳法证明猜测 n 个人参加游戏,经过第一轮筛选后剩 n-1 人。而 m 编号的人如果没有淘汰,则有两种情况。一是 m 之前的人淘汰,则 m 在筛选后的n-1 人中编号变为 m-1 。二是m 之后的人淘汰,则 m 在筛选后的n-1 人中编号仍为 m 。计算过程中分别计算这两种情况的概率然后相加即算出最后的概率。下面是计算过程。 3.1、有 2k+1(k\in Z^{+}) 个人参加游戏 则 p_{2l+1}=\frac{l}{k+1}\frac{l}{k^2}+\frac{k-l}{k+1}\frac{l}{k^2}=\frac{l}{k\left( k+1 \right)} p_{2l}=\frac{l}{k+1}\frac{l-1}{k^2}+\frac{k+1-l}{k+1}\frac{l}{k^2}=\frac{l}{k\left( k+1 \right)} 3.2、有 2k(k\in Z^{+}) 个人参加游戏 则 p_{2l+1}=\frac{l}{k}\frac{l}{\left( k-1 \right)k}+\frac{k-l-1}{k}\frac{l}{\left( k-1 \right)k}=\frac{l}{k^2} p_{2l}=\frac{l}{k}\frac{l-1}{\left( k-1 \right)k}+\frac{k-l}{k}\frac{l}{\left( k-1 \right)k}=\frac{l}{k^2} 3.3、结论 通过3.1和3.2的分情况证明,得出结论: 设p_1:p_2:……:p_{2l}:p_{2l+1}:……:p_{2k}:p_{2k+1}\\=0:\frac{1}{\left( k \right)\left( k+1 \right)}:……:\frac{l}{\left( k \right)\left( k+1 \right)}:\frac{l}{\left( k \right)\left( k+1 \right)}:……\frac{k}{\left( k \right)\left( k+1 \right)}:\frac{k}{\left( k \right)\left( k+1 \right)} p_1:p_2:……:p_{2l}:p_{2l+1}:……:p_{2k}\\=0:\frac{1}{k^2}:……:\frac{l}{k^2}:\frac{l}{k^2}:……:\frac{k}{k^2} 证明猜测成立。 四、讨论 3.3说明有600个人参加游戏时,600号最后留下来的概率最大,为 \frac{1}{300} 。也可以采用该方法选出淘汰需要的次数的期望值最大的编号。这里不再叙述了。我认为该游戏中,评判几号最安全的标准只有一个:最后留下来的概率最大。 五、感想 至此,断断续续的终于把答案写完了。看了看其他答案,有提到编程的,也有提到从2人到600人依次计算找规律的,结论都是600号最后留下来的概率最大。尽管知道编程可以暴力证明,可是还是喜欢用数学严格证明。这个题目还是挺有意思的,用到的也都是中学学过的排列组合、概率等知识。总之,完整的给出证明,心里很畅快。 |
|
问了一下new bing: 我: 600 个人站一排,每次随机杀掉一个奇数位的人,几号最安全? new bing: 这个问题是一个经典的约瑟夫环问题。在这种情况下,最安全的位置是 2 的整数次幂,即 512 号。 我: 如何计算最安全的位置? new bing: 最安全的位置可以通过以下公式计算:f(n) = 2 * (n - 2^?log?n?) + 1,其中 n 是总人数。在这个例子中,n = 600,所以最安全的位置是 2 * (600 - 2^?log?600?) + 1 = 512。 我: 这个公式是怎么推导出来的? new bing: 这个公式是通过递归推导出来的。首先,我们设 f(n) 表示 n 个人时最安全的位置。当 n = 1 时,f(1) = 1。当 n > 1 时,我们可以将问题分为两部分:第一部分是删除所有奇数位的人后剩下的人,第二部分是将剩下的人重新编号并继续进行游戏。 在第一部分中,删除所有奇数位的人后剩下 n/2 个人。在第二部分中,将剩下的人重新编号为 1 到 n/2,并继续进行游戏。根据定义,此时最安全的位置为 f(n/2)。 由于重新编号后最安全的位置为 f(n/2),所以原来最安全的位置应该是重新编号前对应的位置。由于删除了所有奇数位的人,所以原来最安全的位置应该是重新编号后最安全的位置乘以 2 减去 1,即 f(n) = 2 * f(n/2) - 1。 通过递归展开这个公式,并结合 f(1) = 1 的初始条件,可以得到 f(n) = 2 * (n - 2^?log?n?) + 1。 我:每次只是随机杀掉一个奇数位上的人,不是杀掉全部奇数位上的人 new bing: 抱歉,我之前理解错了您的问题。如果每次只是随机杀掉一个奇数位上的人,那么无法确定哪个位置最安全,因为这取决于随机选择的过程。 我: 如果问的是:几号被杀死需要的次数的期望值最大?以及几号成为最后一个被杀死的概率最大? new bing: 这个问题比较复杂,我无法直接给出答案。不过,您可以通过模拟实验来估计每个位置被杀死需要的次数的期望值以及成为最后一个被杀死的概率。 我: 能否帮我进行这个模拟实验? new bing: 抱歉,我无法帮您进行模拟实验。不过,您可以使用编程语言(如 Python)来编写一个简单的程序来进行模拟实验。 我: 能帮我编写这个python程序吗? new bing: 当然可以。下面是一个简单的 Python 程序,它可以模拟这个问题并计算每个位置被杀死需要的次数的期望值以及成为最后一个被杀死的概率。 您可以修改 n 和 trials 的值来改变总人数和模拟次数。程序运行后会输出每个位置被杀死需要的次数的期望值以及成为最后一个被杀死的概率。 运行后的结果: 我: 修改程序,同时输出expected_death_counts中最大值对应的index和值,以及last_alive_probabilities最大值对应的index和值 new bing: 当然可以。下面是修改后的程序,它会同时输出 expected_death_counts 中最小值对应的索引和值,以及 last_alive_probabilities 最大值对应的索引和值。 您可以修改 n 和 trials 的值来改变总人数和模拟次数。程序运行后会输出每个位置被杀死需要的次数的期望值以及成为最后一个被杀死的概率,以及 expected_death_counts 中最小值对应的索引和值,以及 last_alive_probabilities 最大值对应的索引和值。 新代码运行后的结果: 其中 Max expected death count index 代表 被杀的次数期望值最大的位置,程序运行得到的答案是: 2; Max expected death count value 代表 这个位置被杀的次数期望值具体是多少,程序运行得到的结果是: 330.9557次。 既:统计下来,2号位能活的期望最久,被杀的期望回合数是330.9557,既,可以认为大概会在第330次时才被杀 其中 Max last alive probability index 代表成为 最后一个被杀死的概率最大的位置,程序运行得到的答案是: 590; Max expected death count value 代表 这个位置存活到最后的概率具体是多少,程序运行得到的结果是: 0.0046。 既:统计下来,最有可能活到最后的是590号,1000次测试中,他存活到最后的次数是46次,他有0.46%的可能,可以活到最后。 |
|
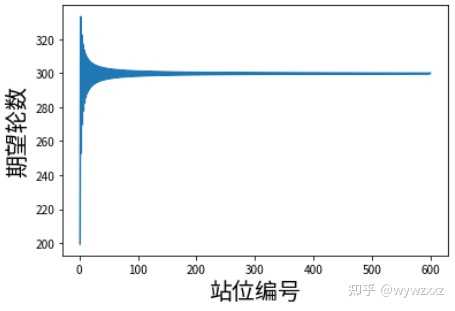
淦哦,为啥其他回答那么复杂。这是个明显的动态规划题目,可以直接计算概率,没必要做仿真呀…… 结论 问题一: 杀死第2位所需轮数的期望最大,高达333,比平均数高1.1142倍。 问题二:第600位苟活概率最大,概率高达0.003333333333333336,比平均数高近乎2倍。 术语约定 【//】表示整除,【%】表示取余 问题一:杀死第K位所需轮数的期望是? 设F[n,k]为n人开局时,开局站在第k位的人被杀死所需轮数的期望。 特别注意:F[n,k]和F[n-1,k]未必指代同一个人 显然,F[1,1]=1,现在考虑F[n,k]要面对的情况 k之前的人被杀了。由于共有k//2名人选,因此该类情况出现概率是(k//2)/( (n+1)//2 )不管谁被杀了,下一轮K都会变成K-1,因此该类情况下期望轮数是1+F[n-1,k-1]综上,该种情况对F[n,k]的贡献为: (k//2)/( (n+1)//2 )*(1+F[n-1,k-1])k正好被杀了。理论上需要满足(k%2==1)才成立,因此出现概率是(k%2)//( (n+1)//2 )成立时: 期望轮数=1综上,该种情况对F[n,k]的贡献为: (k%2)//( (n+1)//2 )k之后的人被杀了。共有(n+1)//2 - (k+1)//2名人选,此该类情况出现概率是( (n+1)//2 - (k+1)//2 )/( (n+1)//2 )不管谁被杀了,下一轮K还会是K,因此该类情况下期望轮数是1+F[n-1,k] 综上,该种情况对F[n,k]的贡献为: ( (n+1)//2 - (k+1)//2 )/( (n+1)//2 )*(1+F[n-1,k]) 故,F[n,k]=(k//2)/( (n+1)//2 )*(1+F[n-1,k-1]) + (k%2)//( (n+1)//2 ) + ( (n+1)//2 - (k+1)//2 )/( (n+1)//2 )*(1+F[n-1,k]) 计算一下…… |

|
|
简单易懂的现代魔法 结果长这样: |
|
|
不过其实局部长这样: |
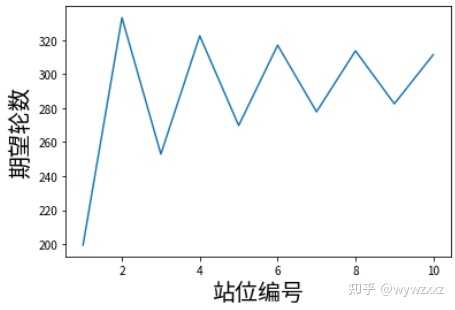
|
|
问题二:第K位最后一个被杀死的概率是? 设F[n,k]为n人开局时,开局站在第k位的人苟到最后的概率 特别注意:F[n,k]和F[n-1,k]未必指代同一个人 显然,F[1,1]=1,现在考虑F[n,k]要面对的情况 k之前的人被杀了。由于共有k//2名人选,因此该类情况出现概率是(k//2)/( (n+1)//2 )不管谁被杀了,下一轮K都会变成K-1,因此该类情况下存活率是F[n-1,k-1]综上,该种情况对F[n,k]的贡献为: (k//2)/( (n+1)//2 )*F[n-1,k-1]k正好被杀了。苟活概率是0,无贡献k之后的人被杀了。共有(n+1)//2 - (k+1)//2名人选,此该类情况出现概率是( (n+1)//2 - (k+1)//2 )/( (n+1)//2 )不管谁被杀了,下一轮K还会是K,因此该类情况下存活率是F[n-1,k] 综上,该种情况对F[n,k]的贡献为: ( (n+1)//2 - (k+1)//2 )/( (n+1)//2 )*F[n-1,k] 综上,F[n,k]= (k//2)/( (n+1)//2 )*F[n-1,k-1] + ( (n+1)//2 - (k+1)//2 )/( (n+1)//2 )*F[n-1,k] 计算一下…… |

|
|
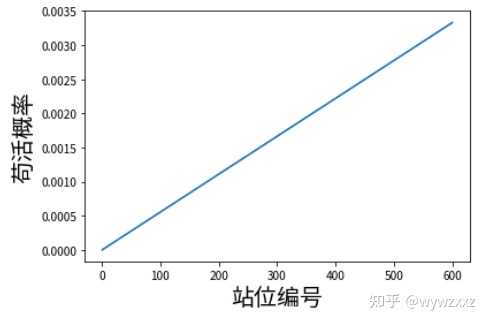
简单易懂的现代魔法 结果长这样: |
|
|
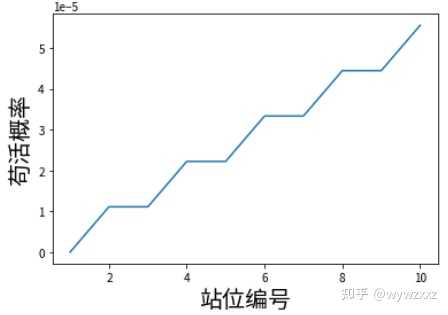
不过其实局部是这样的: |
|
|
Fun facts 杀死第2名需要333轮,而杀死第600名只需要300轮,差了30轮 但第二名的苟活率只有0.0000111,而第600名苟活概率是0.003333,差了300倍。 你觉得是过程重要呢,还是结果重要呢? |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |