| |
|
|
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 自然科学 -> 洛必达法则为何成为禁术？ -> 正文阅读 |
|
|
[自然科学]洛必达法则为何成为禁术？ |
| [收藏本文] 【下载本文】 |
|
如题，高考用会扣分，大学微积分考试还明令禁止使用洛必达法则 （我个人还是好喜欢洛必达法则） [图片] 疑惑产生于大一半期考试之前，刚刚学极限没多久的时… |
|
洛必达法则当然你在大学阶段可以使用。但是只要有水平的出题老师，可以做到让你在大学考试的时候不想用洛必达法则，逼迫你去使用其他的方法求解。 我个人并不反对使用洛必达，甚至非常建议在求极限已经化简比较简单的时候，使用洛必达法则。 一、使用洛必达法则的一些建议基本上大的工作已经处理完毕（使用等价无穷小、泰勒展开、加减凑项、确定项代值）后，发现用其他办法不如洛必达稳定。本身就是比较简单的极限问题，并且求导你很有把握。（大学老师如果禁止你使用洛必达法则，多半有可能是题目太简单了，用洛必达法则可以很稳求解出来）（慎重考虑）发现其他方法并不好做，并且在确定已经有足够的时间下，使用洛必达法则，暴力计算出来。二、为什么我们通常不使用洛必达法则求极限的方法有多种多样，绝大多数问题都可以通过等价替代、泰勒展开、加减凑项、幂指代换等搞定。我们经常高估了我们的计算能力，很多函数求导本身过分就很复杂，求导之后的结构更加复杂，见例题1。但是有一些题目，虽然求导很复杂，但是我们可以保留求导符号使用洛必达法则，见例题3。有时候判断极限是否是0/0型和 ∞/∞" role="presentation">∞/∞\infty/\infty 型也不容易，一旦判断错误，这道题直接就错了。有一些题目，使用洛必达法则，会有着意想不到的效果，见例题2。三、与洛必达法则有关经典极限例题（选自专栏微积分每日一题） 微积分每日一题?www.zhihu.com/column/c_1310152472963874816 例题1：不适合使用洛必达法则 求极限：limx→0(3+x)x−3xx2." role="presentation">求极限：求极限：limx→0(3+x)x?3xx2. \large\bbox[#EFF,50px, border:1px solid 1] {\displaystyle\text{求极限：}\lim_{x\rightarrow 0} \frac{\left( 3+x \right) ^x-3^x}{x^2}. } 比如这道看上去很简单的问题，你可以看出几种方法进行对比，洛必达法则相比而言是比较复杂的： |
|
|
不适合使用洛必达法则的例题例题2：非常适合使用洛必达法则 求极限：limx→0e(1+x)1x−(1+x)exx2." role="presentation">求极限：求极限：limx→0e(1+x)1x?(1+x)exx2.\large\bbox[#EFF,50px, border:1px solid 1] {\displaystyle{ \text{求极限：}\lim_{x\rightarrow 0} \frac{\mathrm{e}^{\left( 1+x \right) ^{\frac{1}{x}}}-\left( 1+x \right) ^{\frac{\mathrm{e}}{x}}}{x^2}.} } 这道题应该来说是一道知乎名题，使用洛必达法则可能是最容易的求解方法了： |
|
|
适合使用洛必达法则的例题例题3：适合使用洛必达法则，但是不需要把求导结果展开 求极限：limx→0(1+x)1x−e⋅ln⁡(1+x)xx2." role="presentation">求极限：求极限：limx→0(1+x)1x?e?ln?(1+x)xx2. \large\bbox[#EFF,50px, border:1px solid 1] {\displaystyle\text{求极限：}\lim_{x\rightarrow 0} \frac{\left( 1+x \right) ^{\frac{1}{x}}-\mathrm{e}\cdot \frac{\ln \left( 1+x \right)}{x}}{x^2}. } 比如这一道题的解法2，就是一个洛必达法则的妙用，但是我们需要有强大的功底，知道这样使用洛必达法则也是可以的，铺垫见紫色文字： |
|
|
适合使用洛必达法则，但是我们不需要把求导结果展开的例题例题4：适合使用洛必达法则，但需要联合其他技巧 求极限：limx→1(1+1x)x(1+x)1x−4(x−1)2." role="presentation">求极限：求极限：limx→1(1+1x)x(1+x)1x?4(x?1)2.\large\bbox[#EFF,50px, border:1px solid 1] {\displaystyle{ \text{求极限：}\lim_{x\rightarrow 1} \frac{\left( 1+\frac{1}{x} \right) ^x\left( 1+x \right) ^{\frac{1}{x}}-4}{\left( x-1 \right) ^2}.} } 这道题虽然洛必达法则不是最重要的求解技巧，但是在拉格朗日中值定理处理完极限之后，还是要考察求导的基本功（洛必达法则）了： |
|
|
适合使用洛必达法则，但需要联合其他技巧的例题例题5：非常适合使用洛必达法则的极限题 求极限：L=limx→1(1−x)(1−x3)⋅⋯⋅(1−xn)(1−x)n−1." role="presentation">求极限：求极限：L=limx→1(1?x)(1?x3)???(1?xn)(1?x)n?1.{ \bbox[#EFF]{\boxed {\displaystyle { \text{求极限：}L=\lim_{x\rightarrow 1} \frac{\left( 1-\sqrt{x} \right) \left( 1-\sqrt[3]{x} \right) \cdot \cdots \cdot \left( 1-\sqrt[n]{x} \right)}{\left( 1-x \right) ^{n-1}}. } }}} 这道题我采用了两种方法求解，第一种方法巧妙地将极限写成多个乘积极限的形式，并对每个极限采用洛必达法则，得到极限后，利用极限四则运算法则即可得到答案。如果采用换元技巧，则难度上大得多了： |
|
|
非常适合使用洛必达法则的极限题四、与洛必达法则有关的证明题例题1：中间过程运用洛必达得到题目暗示结构 设f(x)是定义区间(0,+∞)内的具有二阶连续导数的函数，且|f″(x)+2xf′(x)+(x2+1)f(x)|⩽1.证明：limx→+∞f(x)=0." role="presentation">设是定义区间内的具有二阶连续导数的函数，且证明：设f(x)是定义区间(0,+∞)内的具有二阶连续导数的函数，且|f″(x)+2xf′(x)+(x2+1)f(x)|?1.证明：limx→+∞f(x)=0.\large \color{}{ \bbox[#EFF]{\boxed {\displaystyle \text{设}f\left( x \right) \text{是定义区间}\left( 0,+\infty \right) \text{内的具有二阶连续导数的函数，且} \\ \left| f''\left( x \right) +2xf'\left( x \right) +\left( x^2+1 \right) f\left( x \right) \right|\leqslant 1. \\ \text{证明：}\lim_{x\rightarrow +\infty} f\left( x \right) =0. }}} 这道题洛必达法则起到了中间过程的作用，目的是求构造函数的导数从而得到题意中的结构： |
|
|
洛必达法则作为证明题的中间过程例题2：先利用洛必达法则一次后，再利用其他手段求解 求极限：L=limx→0tan⁡(ex−1)−etan⁡x+1x4." role="presentation">求极限：求极限：L=limx→0tan?(ex?1)?etan?x+1x4.\large \color{}{ \bbox[#EFF]{\boxed {\displaystyle {\text{求极限：}L=\lim_{x\rightarrow 0} \frac{\tan \left( \mathrm{e}^x-1 \right) -\mathrm{e}^{\tan x}+1}{x^4}.} }}} 这道题先利用洛必达法则一次之后，再利用其他手段巧妙进行求解。本质上这是因为我们对3阶的无穷小量更加熟悉了： |
|
|
先利用洛必达法则一次后，再利用其他手段求解五、含有变限积分的极限问题 很多含有变限积分的极限问题，第一步往往需要洛必达法则打开变限积分（复杂的问题往往需要先换元简化被积函数），之后再利用其他的办法求解。 例题1：直接利用洛必达法则求解含有变上限积分的极限 求极限：L=limx→0(1+∫0xet2dtex−1−1sin⁡x)." role="presentation">求极限：求极限：L=limx→0(1+∫0xet2dtex?1?1sin?x).{ \bbox[#EFF]{\boxed {\displaystyle { \text{求极限：}L=\lim_{x\rightarrow 0} \left( \frac{1+\int_0^x{\mathrm{e}^{t^2}}\mathrm{d}t}{\mathrm{e}^x-1}-\frac{1}{\sin x} \right) .} }}} 这道题你做的时候就会发现，直接洛必达来做最方便，如果你要判断是否拆开来分别求极限时，反而容易出错： |
|
|
直接利用洛必达法则求解含有变上限积分的极限 此外，下面是一些变限积分收录的问题，可以阅读与洛必达法则相关的问题： MathHub：变限积分类问题习题荟萃--微积分每日一题特别版35 赞同 · 0 评论文章 |
|
|
看完这些之后，你是否对洛必达法则有了一定新的认识呢？ |
|
|
|
|
之前正好写过文章说洛必达这事。 对于高中生而言，不一定可以用，而且没必要，详见如下文章。 【洛必达】一篇文章，给高中生讲清楚洛必达7477 赞同 · 377 评论文章 |
|
|
对于大学生而言，记得之前有人说过“数院的学生不需要洛必达”。[1] 但是，这么好用的求极限的工具，为什么不用？ 但凡是求极限，只要是不定式（ 00" role="presentation">00\dfrac{0}{0} 或 ∞∞" role="presentation">∞∞\dfrac{\infty}{\infty} 的形式），并且极限存在，就直接洛。 不过，这么好用的东西，也有很多小问题。 首先，很多人根本没有看清是不是不定式，比如 limx→0ex−1x+1" role="presentation">limx→0ex?1x+1\lim_{x\to 0}\dfrac{\mathrm{e}^x-1}{x+1} ，这时候用洛必达，用一个错一个。用错之后还有人会上知乎提问，为什么洛必达失效了？ 除此之外，还有很多比洛必达更好用的求极限的方法，比如等价无穷小或是泰勒展开式。比如 limx→0tan⁡x−sin⁡xx3" role="presentation">limx→0tan?x?sin?xx3\lim_{x\to 0}\dfrac{\tan x-\sin x}{x^3} ，用洛必达也可以，但是用等价无穷小就方便得多，只要注意到 tan⁡x−sin⁡xx3=sin⁡x(1−cos⁡x)x3cos⁡x∼x⋅12x2x3=12." role="presentation">tan?x?sin?xx3=sin?x(1?cos?x)x3cos?x～x?12x2x3=12.\dfrac{\tan x-\sin x}{x^3}=\dfrac{\sin x(1-\cos x)}{x^3\cos x}\sim\dfrac{x\cdot\dfrac{1}{2}x^2}{x^3}=\dfrac{1}{2}. 还有一些比较奇怪的题目，用洛必达估计会洛出一口血。比如 limx→0sin⁡tan⁡x−sin⁡sin⁡xx3" role="presentation">limx→0sin?tan?x?sin?sin?xx3\lim_{x\to 0}\dfrac{\sin\tan x-\sin\sin x}{x^3} ，这时候根据拉格朗日中值定理，存在 ξ∈(sin⁡x,tan⁡x)" role="presentation">ξ∈(sin?x,tan?x)\xi\in(\sin x,\tan x) ，使得 sin⁡tan⁡x−sin⁡sin⁡x=cos⁡ξ⋅(tan⁡x−sin⁡x)," role="presentation">sin?tan?x?sin?sin?x=cos?ξ?(tan?x?sin?x),\sin\tan x-\sin\sin x=\cos\xi\cdot(\tan x-\sin x), 并且当 x→0" role="presentation">x→0x\to 0 时， ξ→0" role="presentation">ξ→0\xi\to 0 ， cos⁡ξ→1" role="presentation">cos?ξ→1\cos\xi \to 1 ，再应用上面的结论即可。 所以，个人建议，遇到复杂的不容易求导的极限，应该优先考虑用等价无穷小、泰勒展开或是Stolz定理[2]等方法，做题会更快一些。 实在没有办法，再用洛必达来做，并且还要注意一定要是不定式。 不过，“洛必达”并不是什么要禁止的东西，都是求极限的工具，总是用得上的。 参考^出处忘了，知道的话可以评论区提醒一下我^懒得举例了 |
| 高考阅卷组：我们为什么不鼓励你用超纲解法答题62.8 万播放 · 333 赞同视频 |
|
|
? 大学的高等数学里不让用洛必达法则可能是命题老师为了考查大家对「极限」这个数学工具的理解和应用，也有可能是像其他答主那样讲的命题老师水平有问题，这个我不做评论； 高考当中我们不鼓励用类似于「洛必达法则」这类超纲知识的原因还是非常明确的：主要出于公平性考虑。 利益相关： 实际上教育部考试中心对于超纲知识在高考当中的态度，简单来说可以被归结为3句话：教材内容不引导，教学过程不延伸，阅卷标准不鼓励。 我们之所以对超纲内容采用如此谨慎的态度，其实有一个价值观层面的原因：在一场全国范围内标准化的考试中如果鼓励超纲解法，违背了考试的公平性原则。 01 公平：高考阅卷为什么不鼓励超纲解法？ 关于「什么是公平」这个问题当然是见仁见智，如果大家未来去了解人类政治思想史的话，关于这个问题的答案就是左派和右派的主要分歧。 右派一般主张能者多劳，多劳多得，这就是公平，具体到高考上，那就是我会用洛必达法则这是我的本事，我的老师能教我那是他的本事。 我的老师凭本事教，我有本事学会，所以大家凭本事得分，你没本事学这种东西得不着分，那是你活该。 可是同学们，咱们在这儿停一下，我来问你：你能在高中就学到洛必达法则，这真的完全是你个人能力的体现吗？ 今天中国的教育资源是非常不平等的，深圳龙华区教师招聘都是985硕士起步，耶鲁和普林斯顿的博士也上不封顶，这些老师当然是有能力教你洛必达法则的； 但，贵州革命老区的乡村中学呢？ 那里的乡村教师有很多甚至是中专毕业，那里的孩子学会链式法则就已经很不容易了，如果我们在阅卷过程中鼓励、甚至放任大家开始无限制地用这种超纲解法往下卷，你的解题工具越来越高级，我的题目出的越来越难，那偏远山区的孩子怎么办？ 到时候上了考场，你用了洛必达法则，他用了泰勒三阶展开，我交了白卷，咱仨都有光明的未来？ 你凭借自己朴素的情感，来告诉我：这合理吗？ 从公平性角度出发，我到底能不能在阅卷过程里鼓励这种倾向？ 02 统一：高中教材为什么不直接教大学洛必达法则？ 其实，同学们以后在问「考场上能不能用洛必达法则」这种问题时，你不如换个角度问一问：高中教材里能不能讲洛必达法则？ 其实我在《应试数学：命题人想考什么》这本书的序言里就说过，在高考这场游戏里，教材编委、高考命题组还有高考阅卷组这三拨人其实是行动一致的。大家提到一些超纲解法时总说：这个方法用起来既正确、又方便，凭什么你们评分细则不鼓励？ 如果事情真像你说的那么简单，洛必达法则真这么好用，那教材直接讲了那多好。 为什么教材不讲？那是因为就中国目前的现实国情来说，你在高中普及性地推广这么高难度的知识，教育贫瘠地区的老师是教不动的，学生也是学不懂的。你把这些东西纳入高考，就几乎直接宣判了这些地区考生的落榜。 03 选拔：不鼓励超纲考法是否违背高考「为国选材」的作用？ 我知道有些同学会说：那高考不是为国选材嘛？你这种放着高端知识不用，那我们怎么选拔最优秀的人才以后去搞科研呀？ 这个问题问的很好，但是你所谓的那种「最优秀的人才」，不是我们高考真正要筛选的人，实际上高考只需要筛选出一般优秀的人就可以了，公平性还是最重要的。 如果你觉得自己很厉害，高中这种常规的知识显不出自己的能耐，那么出门左转，中科大有少年班，大部分985高校都有强基计划，你甚至还可以去参加高水平的各类竞赛保送，那里才是你的舞台。你到了那个地方，洛必达法则随便用，不过你要学的东西，也肯定绝对不止洛必达法则这么简单。 所以，我们其实不鼓励同学们在高考这么一个全国统一的标准化考试里，拿着一个半懂不懂的洛必达法则对贫困山区那些教育资源不如你的孩子降维打击；强基计划、高端竞赛，那里有更广阔的天地可以让你施展拳脚。 如果同学们觉得自己够厉害，在中国的考试制度设计里为你留出了竞争空间，你可以去金字塔顶尖竞争； 但是如果你觉得自己能力有限，选择了参加高考，那到了考场上，就要按照《课程标准》的要求，老老实实做人，认认真真答题。 |
|
你这张图不行 太low了，有本事让你们老师把下面这张图ban了。 |
|
|
|
|
虽然有些电子包浆， 但这几张梗图我还是收下了： |
|
|
|
|
|
|
|
|
|
|
|
|
|
只说大学，但凡不让用洛必达的考试，都是因为出题者水平低下，或者态度不端正，连一道用不了洛必达的题都编不出来。只要做求极限的题做的多了，让你用洛必达你都不敢用，直接自己就把洛必达封印了，要么就是洛个五分钟也洛不完，要么就是根本洛不了，逼你用泰勒，拉格朗日，导数定义等等去做。 现在这些高校的老师，一个个在教学工作上都懒得要死，年年考试卷都是往年试题的排列组合，改个数就完事了，想考察泰勒公式求极限，甚至都懒得出一道不用泰勒公式就没法做的题，纯纯的耍流氓 |
|
挺搞笑的 这法则就是为了方便才被发现的 结果现在因为太过方便而不给用了 而且居然还要减分和ban掉？ 我直接骂出题人偷懒 我上大学的时候洛是洛不动的，考试时洛一道题那后面的题就别想了，反而夹逼准则之类的更方便迅速，用这种方式不比直接禁了的有更好的学习效果？ 建议查一查是不是出题人在摸鱼 |
|
高考我不太好做评价。我单纯从大学数学的角度揣测一下。 我认为这一规定可能是为了考察你对极限的定义的理解，尤其是 \epsilon,\delta 版本的定义，而不是说去考察你能把能把某个极限算出来。 一个很相似的问题是：用黎曼分割法求出 \int_{x=0}^1 x^2dx 。 做过这类题的同学都知道这个过程有多麻烦。先将0到1切成n小份，每份长度是1／n。在每一个1/n的小区间里，取x^2的最大值再乘以1/n。然后将n个乘积加起来。最后再让n趋近于无穷，得出的极限就是这个定积分的值了。 一个很自然的问题是：为啥要搞这些？弄一个微积分第二基本定理，都不用笔十秒钟就出来了。 后来我学的越来越深的时候才明白：微积分第二定理很多时候只是一个计算的捷径，黎曼求和才是积分的实质啊----前面的那个问题就是为了考察你是不是理解了定积分究竟是什么。 这个真心不是脱裤子放屁。你越往下学，要面对的积分就越复杂，你可能就再也没有微积分第二定理这种简单的公式可以代入了。这个时候就需要你利用黎曼和这样的方法来处理问题了（你以后或许会接触到蒙特卡洛）。甚至你要用黎曼和来探讨积分是不是存在的。 或者这么说：微积分第二基本定理只是一套功法的某一招式，黎曼求和、积分的定义才是这套功法的真义。万变不离其宗。 我觉得极限-洛必达法则和微积分第二定理-黎曼求和是一样的关系。不让用洛必达法则这个要求应该是想要告诉你极限的 \epsilon,\delta 定义也是必须掌握的，不能只知道计算的捷径。 当然，我也不知道这么搞是不是真的有用----毕竟很多同学刚一碰微积分的课本就弃疗了。 权当这个是老师的执着吧。 再补充一下，我觉得如果说是一个负责任的高数老师，即便是让学生用洛必达，也绝对不会是让学生无脑套公式轻松得分的那种。 高数这门课的意义有二。一，让学生掌握一些所有理工科都需要基本的微积分概念。二，让学生对于高等数学的严谨性有一定的了解。 很多理工科的学生即便不怎么用写证明，以后也是要进行很多推导的。所以这门课应该要告诉学生什么样的推导是没有瑕疵的。 其中想传达的一个重要信息是：定理不能无脑用；必须检查先决条件。 所以，如果说高数里面出一道大题，允许学生使用洛必达，那么学生一定要先强调 \frac{f(x)}{g(x)} 是符合 \frac{0}{0} 或者 \frac{\infty}{\infty} 这一要求的。或许题目还会简单要求学生回答一下函数趋近于 \infty 的定义是什么。 如果说你不检查这个先决条件直接套用洛必达，我觉得要扣掉相当的分数。 这就是高等数学，除了得数，更重要的是让你知其然还要知其所以然。 那你说我就想无脑用行不行。这个呢，在考试中也就是丢点分。在以后的工作中，你要是想当然漏算了一些点，造成的结果可能是灾难性的。这里其他学科，尤其是工科，和纯数学截然不同；你搞的东西是要在现实生活中直接产生影响的。 |
|
看见题，洛不洛？洛了再说！ 此刻我就是小曹植 ，《洛神赋》写起走 |
|
|
然后就出现了一大批反洛斗士 |
|
|
|
当然少不了我们的葛军giegie |
|
|
|
|
|
|
|
|
然而，我们有以下定理，证明洛必达确实是万能之法。 |
|
|
12.17更新，等答主考完四级会回来补上面的那道多重根号求极限的题目。 12.18 四级考完了，来更新啦 除了L'hospital法则，答主就只想到用Taylor公式了，于是就做起了数学民工，一层一层的硬算捏。 因为第一题和第二题思路一模一样，为了减轻答主的吐血程度，下面只写了第二题 |
|
|
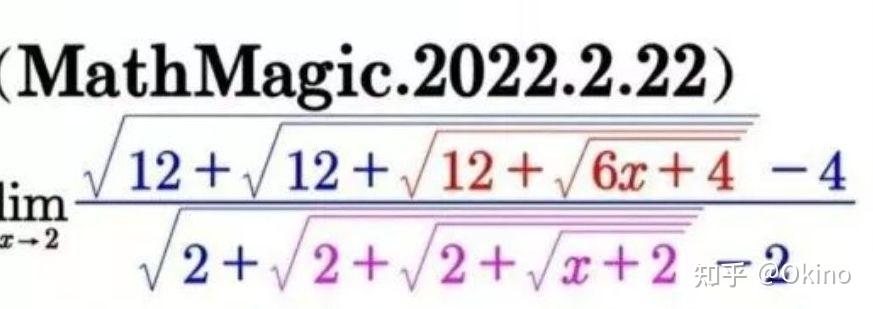
懒得用公式编辑器，就写在纸上了 |
|
|
评论区有朋友 @乱舞春秋 指出用这样的方法 |
|
|
看了以后，对那个重复代换的步骤，我感觉有点怪怪的，于是就用反证法证明了一下，发现这样做是不行的。 |
|
|
令人沮丧的是，我只是证明了这个方法的错误，但是说不清它的错误的原因在哪。如果有dalao路过的话，可以解释一下它错在哪了吗 12.25更新 大家圣诞节快乐！ 有朋友 @九云 给出了另外一种解法，我觉得很巧妙，在这里贴出来啦。 |
|
|
运用了一个如下的等价替换： 当x\rightarrow0时，有\sqrt{x+1}-1\sim x/2 成立 运算思路与平常相反，不是从内层到外层，而是从外层到内层。 还有重要的一点是，每当算完一次外层的根号，再通过恒等变换可构造出一个与上一步形式相同的式子，也就是每一步都可以构造出上面的那个等价替换，进而大大减少计算量。 这也让我对上面那个另外一个朋友的做法产生了一点思考。第一个朋友是从内层到外层进行恒等变换的，虽然我还是没有弄懂他哪错了，但是从内层到外层运算也是可行的。运用以下这个等价变换: \sqrt{x+1}\sim x/2+1 从内层到外层。 |
|
|
| [收藏本文] 【下载本文】 |
| 自然科学 最新文章 |
| 海南一村民被眼镜王蛇咬死，多名消防员和村 |
| 有哪些不起眼的牢底坐穿兽？ |
| 美国耕地面积比中国大，可为什么粮食产量不 |
| 如何看待同济大学2024国家科技三大奖颗粒无 |
| 假如航母被蓝鲸全速前进撞一下会怎么样？ |
| 你见过最狠的SCI评论是什么? |
| 你在实验室最惊险的瞬间是什么？ |
| 牛顿生活在中国，会有什么成就？ |
| 虎鲸为什么不吃人？ |
| 数学为什么这么可笑？ |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |