| |
|
|
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 自然科学 -> 1+0.1+0.01+0.001+0.0001... 一直下去会在实际中到达 2 吗？ -> 正文阅读 |
|
|
[自然科学]1+0.1+0.01+0.001+0.0001... 一直下去会在实际中到达 2 吗？ |
| [收藏本文] 【下载本文】 |
|
1+0.1+0.01+0.001+0.0001... 一直下去会在实际中到达 2 吗？ 关注问题?写回答 [img_log] 数学 物理学 1+0.1+0.01+0.001+0.0001... 一直下去会在实际中到达 2 吗？ |
|
你去问拼多多呀，这个他最懂了！拼多多玩剩下的。 |
|
|
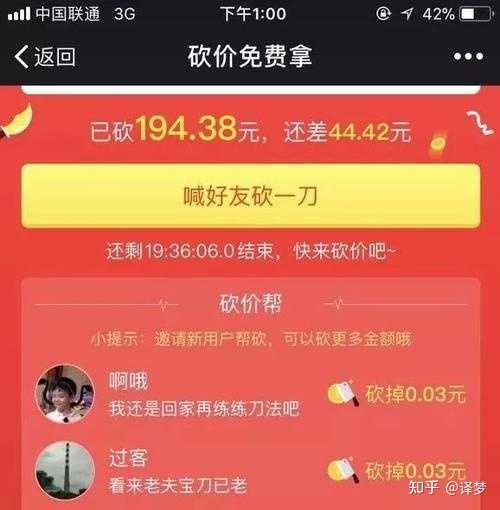
一个200的红包，先给你199.9元，拉10个人即可提现。 你拉了9个人，凑到199.9元，然后拉一个人0.01元，10个人0.1元。 你又拉了9个人，凑到199.99元，然后拉1个人给1个金币，10个金币0.01元。 你又拉了9个人，凑到199.99元加9个金币，然后拉1个人给1个银币，10银币等于1金币。 你又拉了9个人，凑到了199.99元加9金币9银币，然后拉1个人给1个铜币，10铜币等于1银币。 你又拉了9个人，凑到了199.99元加9金币9银币9铜币，然后拉1个人给1铁币，10铁币等于1铜币。 。。。。。。 最后你挂了，200块你还是没拿到！ |
|
|
所以，1+0.1+0.01+0.001+0.0001... 能等于2吗？我也不知道啊！ |
|
如果限于小学数学，有： 0.1=1−0.8−0.1" role="presentation">0.1=1?0.8?0.10.1 = 1 - 0.8 - 0.1 0.01=0.1−0.08−0.01" role="presentation">0.01=0.1?0.08?0.010.01 = 0.1 - 0.08 - 0.01 0.001=0.01−0.008−0.001" role="presentation">0.001=0.01?0.008?0.0010.001 = 0.01 - 0.008 - 0.001 往下以此类推，每行公式右式的最右项，都可以被下一行公式的最左项抵消。 以此代入原式得到： 1+0.1+0.01+0.001+0.0001…=2−0.8−0.08−0.008−0.0008…" role="presentation">1+0.1+0.01+0.001+0.0001…=2?0.8?0.08?0.008?0.0008…1+0.1+0.01+0.001+0.0001\ldots =2 - 0.8 - 0.08 - 0.008 - 0.0008 \ldots 也就是说原式跟2的差距至少是0.8，所以不能达到2。 |
|
一个公比为十分之一的等比数列求和就给兄弟们难住了？ 看到有兄弟说求和公式不适用无限项，宁把最后一项当an，然后就可以得到一个新函数，证明这个函数恒＜2就行了，兄弟们不会高中导数也忘了吧 |
|
嗯，这种问题能成热搜，自证985/211不是平均水平，平均水平显然处于买菜阶段。 小学生解法：把求和结果写成1.111111…，连1.2都不到，再聪明点可以知道1.111111…=10/9 中学生解法：把求和式子看做无穷递缩等比数列求和，套公式，和为1/(1-0.1)=10/9 大学生解法：数列 {1 , 1.1 , 1.11 , 1.111 ...} 显然收敛于10/9 脑经急转弯解法：在二进制，1.111111…=10，相当于十进制的2（进制杂糅） 所以原则上来讲，但凡上过学的稍微动动脑筋都可以知道答案。 九年义务强制教育，我想各位小学肯定上过，但有的人就是不肯动脑筋。 毕竟高考完之后，太多人都累了，智力反弹到幼儿园水平。 这样简单的问题能上热搜，就是信息时代的悲哀，因为信息时代大家脑子被不停刷新的信息塞满，没时间动脑筋。 越反智的话题越有受众，越反智的话题越上热搜。 拼嘻嘻骗的也就这类人（拼嘻嘻砍一刀，越砍数字越小，你砍到地老天荒也就那样） 现在你还敢说学数学只能买菜了吗？ 请您欣赏： |
|
|
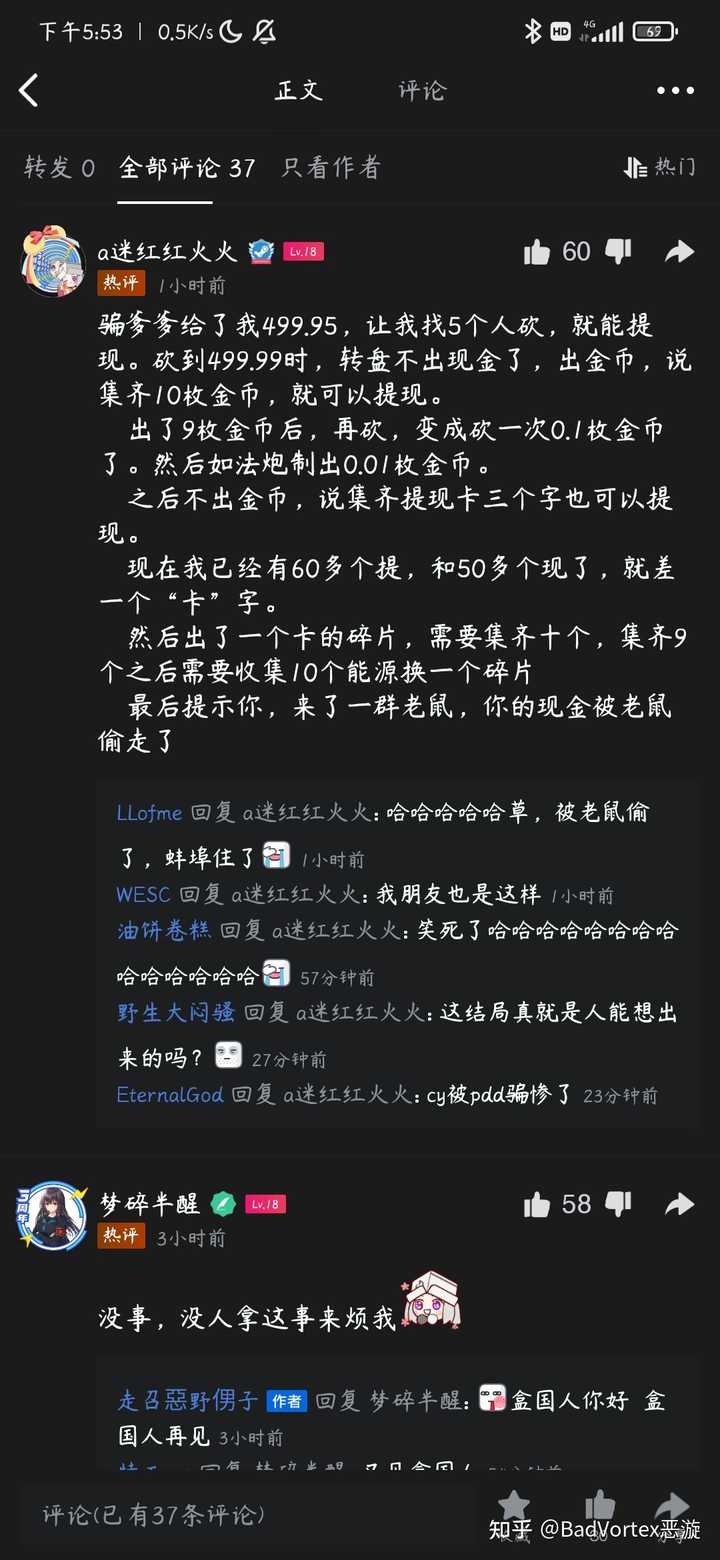
此图感谢网友提供，侵删 更新： 看到评论区有人提出语文解法：庄子好基友惠子的“一尺之捶，日取其半，万世不竭”。 首先我肯定这种具象思维。 但是，具象思维不一定正确。 尤其是在物理世界，宏观层面的具象思维，不能推广到微观层面。 宏观上我们觉得一尺之捶可以无限分下去，微观上却只能分到夸克（目前）。 所以建议大家，数学问题就用数学逻辑思考，避免形象思维的臆测。 |
|
鉴于等比数列求和一般是高中内容，题主可能是初中生，甚至很有求知欲望的小学生，我尽量用简单一点的方法来解释。 设想你手上有两个苹果，记做S=2， 现在挑一个苹果，均匀切五瓣，丢掉四瓣，现在你还剩下一个完整苹果，一个五分之一苹果，S=1.2， 再把刚才那一瓣挑出来，对半切，其中一半均匀切五瓣，丢掉四瓣，现在你还剩下一个完整苹果，一个十分之一苹果，一个十分之一苹果的五分之一，S=1.12 再把刚才最小那一瓣挑出来，对半切，其中一半均匀切五瓣，丢掉四瓣，现在你还剩下一个完整苹果，一个十分之一苹果，一个百分之一苹果，一个百分之一苹果的五分之一，S=1.112 ...... 反复操作之后，你会得到一系列苹果（和渣），也就是一个完整苹果，一个十分之一苹果，一个百分之一苹果，一个千分之一苹果，一个万分之一苹果......，S=1.11111111... 现在，你想想，你已经丢掉了这么多苹果，剩下的苹果有两个苹果这么多么？ |
|
这种事你应该问拼多多啊，他玩儿的贼6 |
|
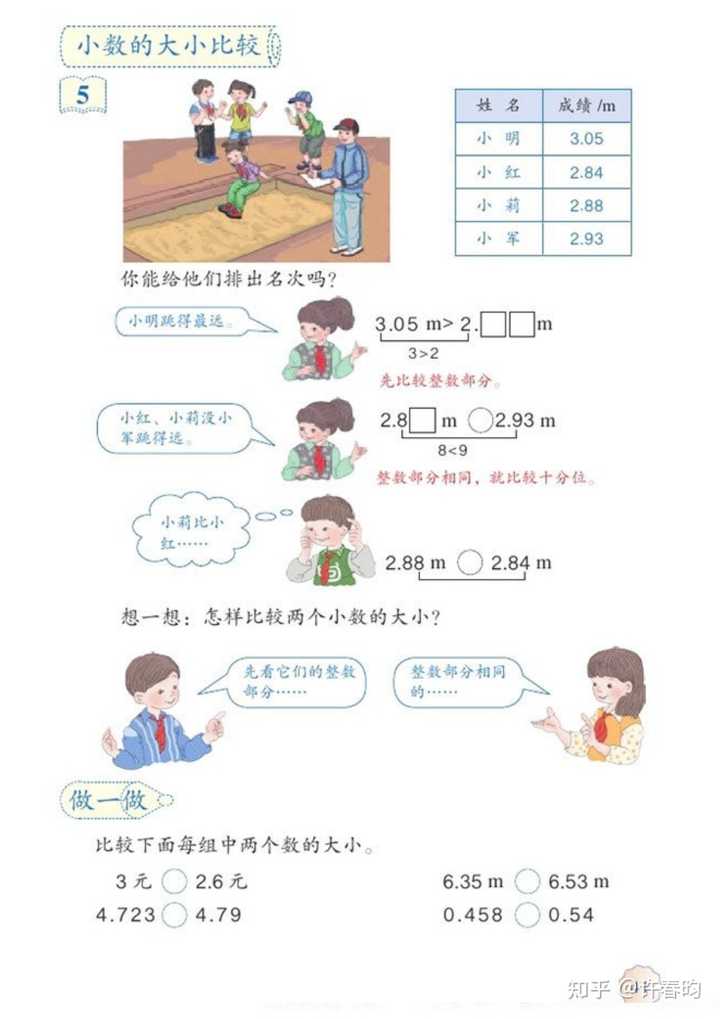
惊呆了，这不是一道小学数学的题目吗？题目如果是 1+0.9+0.09+0.009+0.0009... 和 2 比较那还差不多，而竟然是 1+0.1+0.01+0.001+0.0001...，就是 1.1111111111... 啊，也太夸张了吧，1.2、1.1111111112、1.3、1.4、1.5 都没到，怎么可能到达 2。看来得给题主补补小学数学了。请翻开人教版数学四年级下册课本 35 页和 41 页，好好复习复习。 ① 小数的表示 打开 35 页（见图1)，“做一做”中习题看到没，这就是小数各数位组成的概念，对于题目的： 1+0.1+0.01+0.001+0.0001..." role="presentation">1+0.1+0.01+0.001+0.0001...1+0.1+0.01+0.001+0.0001... 就是1个一，1个十分之一，1个百分之一，1个千分之一，1个万分之一...的和，这正是无限小数各数位的组成，即： 1.1˙=1.111111...=1+0.1+0.01+0.001..." role="presentation">1.1˙=1.111111...=1+0.1+0.01+0.001...1.\dot{1}=1.111111... =1+0.1+0.01+0.001... 显然，这是一个循环小数。 1.1˙" role="presentation">1.1˙1.\dot{1} 和 2" role="presentation">22 谁更大呢，也就是 1.1111111111... 和 2 比较谁大谁小，你会判断了吗？ ② 小数的大小比较 方法一（直接比较）： 翻到 41 页（见图2），复习怎么比较小数大小，先比较整数部分，整数部分相同就比较十分位，十分位相同就比较百分位，依此类推。 题目要比较1.1˙" role="presentation">1.1˙1.\dot{1} 和 2" role="presentation">22 的大小关系，显然整数部分 1 比 2 要小，而且十分位的数字 1 比 9 小[注：因为1.111...为循环小数，我们要再判断此小数下一位是不是数字9]，故 1.1˙<2。" role="presentation">。1.1˙<2。0.0\dot{1}\leq0.1， 得 1.1˙=1.1+0.01˙≤1.1+0.1=1.2<2。" role="presentation">。1.1˙=1.1+0.01˙≤1.1+0.1=1.2<2。\pi的具体数值为3.1415926..." role="presentation">3.1415926...3.1415926...，那么3.1415926...<4" role="presentation">3.1415926...<43.1415926...和4" role="presentation">44之间的一个数字吗？如何用上面的证明方法证明3.1415926...<4" role="presentation">3.1415926...<40.\dot{9} 和 1" role="presentation">11 比较的情况呢？ 别急，请打开人教版五年级下册课本第 77 页（见图3），复习怎么将小数转为分数，然后再比较大小。 我们继续拿 1.1˙" role="presentation">1.1˙1.\dot{1} 和 2" role="presentation">22 比较作例子说明： 由19=0.1˙" role="presentation">19=0.1˙\frac{1}{9}=0.\dot{1} ，得 1.1˙=1+19=109<2，" role="presentation">，1.1˙=1+19=109<2，0.\dot{9} 如何转化为分数和 1" role="presentation">11 比较呢？ |
|
|
图1 小数的表示和数位组成 |
|
|
图2 小数的大小比较 |
|
|
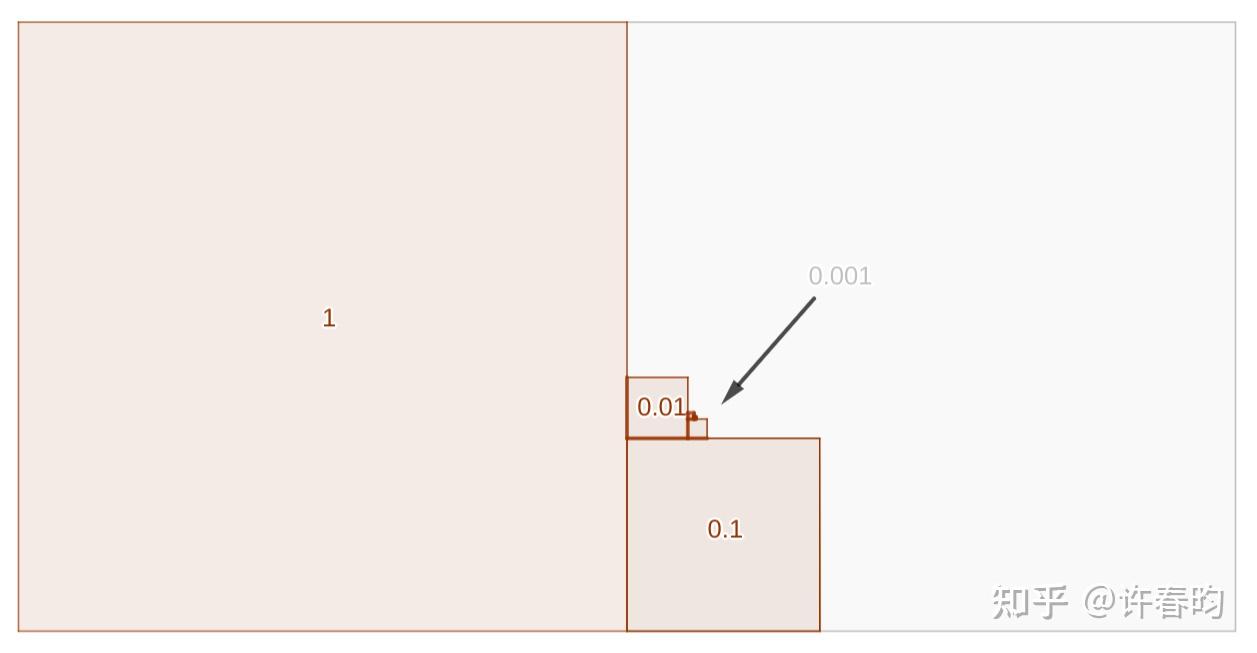
图3 分数和小数的相互转化 ③ 拓展内容（小学超纲知识，可跳过，若感兴趣可进一步钻研） （1）如何严谨证明 0.9˙" role="presentation">0.9˙0.\dot{9} 和 1" role="presentation">11相等 上面提到的用分数论证 0.9˙" role="presentation">0.9˙0.\dot{9} 和 1" role="presentation">11相等的证明方法是对的吗？有没有更严谨的证明方法呢？请参见知乎上已有的详细解答：为什么 0.9 的循环等于 1？，如何严谨地证明 0.9999…=1？。这里不再赘述。 注：数学证明各有不同的严谨性、背景假设和目标受众。对于非数学研究人员来说，将 0.9˙" role="presentation">0.9˙0.\dot{9} 转化为分数相乘等于1的形式，或将整体看作一个未知变量乘10之后求差得到未知变量为1的证明形式，均是正确的证明方法；而对于基础数学研究来说，对 0.9˙" role="presentation">0.9˙0.\dot{9} = 1" role="presentation">11 最严谨的论证则需要用到实数理论。 这些论证形式在奥数教材或数学期刊中都有给出过，维基词条上更是有词条 「0.999...」（ https://en.wikipedia.org/wiki/0.999... ），从最简单到最复杂的近十种证明，都全部列出来，本词条上也强调这些证明都是正确的，只是严谨性和受众目标各不同而已。法国数学家 Jean-Paul Delahaye 也发表过文章《0.999...=1?》（0.999...= 1？），系统性地介绍了从初等数学到高等数学的各种论证形式。 （2）用图形直观表示 1.1˙" role="presentation">1.1˙1.\dot{1} 如图4所示，最大的正方形面积为单位1，小一点是0.1（边长等于单位1对应正方形边长的 110" role="presentation">110\frac{1}{\sqrt{10}} ），再小一点的是0.01（边长等于0.1对应正方形边长的 110" role="presentation">110\frac{1}{\sqrt{10}} ），依次画下去，全部粉红色部分就代表小数1.1˙" role="presentation">1.1˙1.\dot{1}的大小。 白色部分则是第二个单位1的正方形剩下的空间，从直观上看 1.1˙" role="presentation">1.1˙1.\dot{1}比 2" role="presentation">22 小得多，而且越到后面的正方形越挤到下面箭头位置的角落中，1.1˙" role="presentation">1.1˙1.\dot{1}也无法收敛于 2" role="presentation">22 ，毕竟中间还有 1.112，1.12，1.2，1.2˙，1.9˙" role="presentation">，，，，1.112，1.12，1.2，1.2˙，1.9˙1.112，1.12，1.2，1.\dot{2}，1.\dot{9} 等等数字。 |
|
|
图4 用图形表示1.111... |
|
本人是一个高中生，故根据高中所学知识作以回答。 我们可以将其看做是一个以1为首项，0.1为公比的等比数列，得到数列{a_n}通项公式为： a_n=(0.1)^n 故可以得到数列之和为 S_n=a_1(1-q^n)/1-q S_n=10/9(1-0.1^n) 取极限可得S_n=10/9. 以上。 |
|
不会。 limn→+∞an=L" role="presentation">limn→+∞an=L\lim_{n\to +\infty}a_n=L 这个式子的意思是啥？ 或者说，「数列 {an}" role="presentation">{an}\{a_n\} 的极限是 L" role="presentation">LL 」这句话，到底是啥意思？ 题主估计会说：「 an" role="presentation">ana_n 会越来越接近于 L" role="presentation">LL 。」 但是我们举个简单的例子： an=110n" role="presentation">an=110na_n=\dfrac{1}{10^n} 。显然有 limn→+∞an=0" role="presentation">limn→+∞an=0\lim_{n\to+\infty}a_n=0 。 但是如果按照题主的说法，「 an" role="presentation">ana_n 会越来越接近于 L" role="presentation">LL 」，那我是不是也能说 limn→+∞an=−1" role="presentation">limn→+∞an=?1\lim_{n\to+\infty}a_n=-1 ？ 毕竟，随着 n" role="presentation">nn 的增大， an" role="presentation">ana_n 和 −1" role="presentation">?1-1 的距离即 an+1" role="presentation">an+1a_n+1 也会越来越小，那 an" role="presentation">ana_n 不也是越来越接近于 −1" role="presentation">?1-1 嘛qwq。 所以我们又加了一条限制，就是这个看上去不太好理解的句子： 对任意的 0">ε>0" role="presentation">ε>0\varepsilon>0 ，均存在一个 n∈Z+" role="presentation">n∈Z+n\in \mathbb Z_+ ，使得 |an−L|<ε" role="presentation">|an?L|<εL 为 {an}" role="presentation">{an}\{a_n\} 的极限。 这个意思就是， an" role="presentation">ana_n 和 L" role="presentation">LL 之间不只是越来越近，而且还是「想多近就能多近」！ 有了这个限制之后，如果我们再说 limn→+∞110n=−1" role="presentation">limn→+∞110n=?1\lim_{n\to+\infty}\dfrac{1}{10^n}=-1 ，那么取 ε=1145141919810" role="presentation">ε=1145141919810\varepsilon=\dfrac{114514}{1919810} ，可以发现，由于 1">|an−(−1)|=an+1>1" role="presentation">|an?(?1)|=an+1>1|a_n-(-1)|=a_n+1>1 ，故此时并不存在 n∈Z+" role="presentation">n∈Z+n\in \mathbb Z_+ ，使得 |an−(−1)|<ε" role="presentation">|an?(?1)|<εL=0 ，那么就可以取 n=6" role="presentation">n=6n=6 ，此时 |a6−0|=11000000<1145141919810" role="presentation">|a6?0|=11000000<1145141919810-1 并不是这个数列的极限， 0" role="presentation">00 才是。 现在再看看那句话：「只要一直无穷无尽地、不断地加下去，总会越来越大。」 嗯，笑一笑就好啦qwq。 最后，考虑数列 an=∑k=0n110k=1+0.1+0.01+⋯" role="presentation">an=∑k=0n110k=1+0.1+0.01+?a_n=\sum_{k=0}^n\dfrac{1}{10^k}=1+0.1+0.01+\cdots ，就是题目中的数列。 如果你还认为 limn→+∞an=2" role="presentation">limn→+∞an=2\lim_{n\to +\infty}a_n=2 ，我取一个 ε=0.8" role="presentation">ε=0.8\varepsilon=0.8 ，好啦，请你找到一个 n∈Z+" role="presentation">n∈Z+n\in \mathbb Z_+ ，使得 |an−2|<ε=0.8" role="presentation">|an?2|<ε=0.8\lim_{n\to \infty}a_n=\dfrac{10}{9} ，并不是 2" role="presentation">22 。 |
|
这不是一个数学问题， 而是一个 NLP（自然语言处理）或者脑科学的问题。 为什么在知乎，这个问题可以成为热门问题，这说明， 是怎样的感知让人容易产生这种错觉，才是值得思考的。 2021.4.30 补充：由于很多人质疑，既然这不是一个数学问题那么它难道是××问题吗 —— 其实我的意思是：如果从数学的角度看，这个问题根本就是平凡、缺乏意义的，因为只要了解一点有关于无穷级数求和的知识，就可知显然这个级数和的极限值根本就不是 2。 ～ 完 ～ |
|
这个式子小于1.2看不出来？ |
|
相当于你不停地写： 1.1111111 ... 第一位已经是1了，之后只是不停往小数点后面填数。由小学算术知识可知，当各位始终为1时，这个数永远不可能大于等于2 易得，经过无穷的时间，这个数最终会收敛在10/9这个值上 |
|
我们来算一下这个数列求和的精确解. \begin{align} A&=1+0.1+0.01+0.001+\cdots\\&=\sum_{a=0}^{-\infty}{10^a} \end{align} 咦, 这个数列好像是我们高中学过的等比数列呀. 那我们用一下等比数列求和公式? {\displaystyle a+ar+ar^{2}+ar^{3}+\cdots +ar^{n}=\sum _{k=0}^{n}ar^{k}=a\left({\frac {1-r^{n+1}}{1-r}}\right)} 所以 \begin{align} A&=1+0.1+0.01+0.001+\cdots\\&=\sum_{a=0}^{-\infty}{10^a}\\ &=\lim_{a\to-\infty}1\cdot\frac{1-(\frac{1}{10})^{-a}}{1-\frac1{10}}\\ &=\frac{1-0}{\frac{9}{10}}\\ &=\frac{1}{\frac9{10}}\\ &=\frac{10}9\\ &=1.1111111111111111111111111111111 \\ \\ &<2 \end{align} \begin{align} \end{align} 所以啦, 用高中的知识(和一点点极限的知识), 我们就能证明这个数列的极限是 \frac{10}{9} . 是肯定达不到 2 的啦. 另外注意哦, 并不是一直加一个大于零的数就一定会达到某个值. 就比如说这个数列, 就达不到 2 也不是后一项比前一项小就一定会趋于某个值. 比如说 B=\sum_{a=1}^{+\infty}{\frac1a} 就会加到正无穷去, 虽然后一项永远比前一项小. |
|
我说为啥今天这么多人赞我，都两个多月过去了，原来是这个问题又上热榜了，我愿称其为吃饱了撑的 原回答： 究竟是道德的沦丧，还是人性的扭曲，会让一个1.1111111……会不会等于2的问题登上知乎热榜第三 |
|
|
|
|
确实，如果是在二进制中。这样的话有 (1.111\cdots)_2=\left(\sum_{i=0}^\infty{1\times2^{-i}}\right)_{10}=\left(\frac{1-2^{-\infty}}{1-2^{-1}}\right)_{10}=(2)_{10}=(10)_2 不过一般情况下我们说的都是十进制，这样的话这个答案应该是1.111...，也就是10/9。 好吧，不用上图这个花里胡哨的式子，简单点：对于序列2^0,2^{-1},2^{-2}\cdots ，也就是 (1)_2,(0.1)_2,(0.01)_2,\cdots 怎么求和？ 令s=2^0+2^{-1}+2^{-2}+\cdots\\ \\ \ \ \ \ \ 则2^{-1}s=\ \ \ \ \ \ \ \ \ \ 2^{-1}+2^{-2}+2^{-3}+\cdots\\ 相减，得\left(1-2^{-1}\right)s=2^0-2^{-\infty}\\ 即得s=\frac{2^0-2^{-\infty}}{1-2^{-1}}=2 大功告成。 |
|
|
| [收藏本文] 【下载本文】 |
| 自然科学 最新文章 |
| 海南一村民被眼镜王蛇咬死，多名消防员和村 |
| 有哪些不起眼的牢底坐穿兽？ |
| 美国耕地面积比中国大，可为什么粮食产量不 |
| 如何看待同济大学2024国家科技三大奖颗粒无 |
| 假如航母被蓝鲸全速前进撞一下会怎么样？ |
| 你见过最狠的SCI评论是什么? |
| 你在实验室最惊险的瞬间是什么？ |
| 牛顿生活在中国，会有什么成就？ |
| 虎鲸为什么不吃人？ |
| 数学为什么这么可笑？ |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |