| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 现代数学和理论物理已经发展到怎样一个令人震惊的水平了? -> 正文阅读 |
|
|
[时尚穿搭]现代数学和理论物理已经发展到怎样一个令人震惊的水平了? |
| [收藏本文] 【下载本文】 |
|
现代数学和理论物理已经发展到怎样一个令人震惊的水平了? 关注问题?写回答 [img_log] 数学 物理学 理论物理 现代物理学 现代数学 现代数学和理论物理已经发展到怎样一个令人震惊的水平了? |
|
来简单说一下当前可以确认的理论物理的高度。我们最早的理论物理是为实验服务的。在那个年代,我们依然处于做大量的实验,然后总结规律的阶段。所以在这一阶段涌现出了一系列比较初等的定律,比如 热力学第n定律Snell 定律(光的折射定律)万有引力定律Coulomb 定律(静电相互作用)Faraday 定律 (电磁感应定律) 等等。这个时候物理学理论和其它任何科学分支的理论没有本质上的差别。 后来,我们开始发现不同的定律之间有一些相同之处,尤其是发现电学和磁学之间的巨大相似性,进而发现原来电和磁是同一样东西。于是我们开始做抽象,把电学和磁学(以及一部分波动光学)的规律都吸收到了一套理论中,这就是 Maxwell 的电磁理论。这一阶段的画风是这样的 一切电磁相关的现象均可被 Maxwell 电磁理论描述一切引力相关的现象均可被 Einstein 引力理论描述一切热学相关的现象均可被 统计理论描述 ………… 再接下来,我们还发现不同的理论之间还有一些相同之处。于是我们开始了进一步的抽象,创造了所谓的 theory generator,或者说是一种通用的,用于生产理论的方法。典型的案例包括 Lagrange 动力学,Hamiltonian 力学等等。这一阶段的画风是这样的 一切经典理论均可由如下原理生成: \delta S = 0, \ \ \ \text{where}\ \ \ S = \int\mathcal L 这里面 S 是作用量, \mathcal L 被称为 Lagrangian。为了得到 Maxwell 电磁理论,你只需要\mathcal L = F^2 / 4 ,为了得到广义相对论,你只需要\mathcal L = R 。是的,你只要指定一个 Lagrangian,然后上述原理就可以自动给你生成一个理论。 这看上去好像用处不是非常大。事实上在牛顿那个年代之后不久,这种方法的雏形就已经出现了。不过真正让它焕发光彩的是 1918 年(正好100年前)的一件大事:著名数学物理学家 Emmy Noether 提出了 Noether 定理,这一定理利用上述原理证明了 Lagrangian 的对称性可以导致守恒量。 这是非常强大的一条数学定理。要知道,物理学的对称性几乎就等同于普适性,而普适性是一套理论作为科学理论的底线级要求。所以,这条定理几乎就是在说任何物理理论里均存在守恒量,并且只要你写出 Lagrangian,我们就能用一套标准流程把这些守恒量找出来! 一个重要的例子就是能量。能量是与时间对称性绑定的一个守恒量,或者换句话说,我们会把能量定义为与时间对称性相关联的那个守恒量。更具体一点,我们写出一个具有时间对称性的 Lagrangian,Noether 定理就能给出一个对应的守恒量,而这个量就被定义为能量。自此,能量守恒便不再是所谓的经验定律,而是一条有严格证明的定理。 除了上述的两个经典的 theory generator,现在我们熟知的量子力学(当然你得把 Schroedinger 方程写成 \mathrm i\partial_t\psi = \mathcal H\psi 这样的抽象形式),量子场论,以及曾经火过两回的弦理论,都是 theory generators。它们当中都有类似于 Lagrangian 或 Hamiltonian 这一类的抽象的量,在给定这些量的情况下,就自动生成理论。 总结来说,我们最早根据实验得到了一些定律,然后发现定律之间有共同点,于是把这些定律抽象成了理论,然后又发现理论之间也有共同点,于是又抽象成了 theory generator。反过来,给定 theory generator 里面所需要的量,它就会自动给我们生成理论,将理论应用于不同的情景,我们又可以获得具体的一些定律。 其实现在 theory generators 的威力还远不止于此。不过这已经涉及到目前最前沿的理论物理。你点个赞,我看看要不要继续写。 感谢大家的热情,那我更一波。不过这些内容可能就未必像之前那么好懂,也未必如 Noether 定理一般精彩,不过我会尽量写得通俗易懂一些。 一般的 Lagrangian 是某个动力学变量(比如粒子的位置 x 或者某个场 \varphi(x) )以及它的导数(比如速度 \dot{x} 或者场的梯度 \partial_\mu\varphi )的函数。我们通常把含导数的项称为动能项,其余的称为势能项。 先来看动能项。我们发现无论是哪一种理论,动能项往往能够被写成一阶导数的平方,比如通常经典力学里的动能项 mv^2/2 就是速度的平方,再比如标量场的动能项 \partial_\mu\varphi\partial^\mu\varphi 也是一阶导数的平方。个别例子中有出现仅仅是一阶导数,没有平方,比如 Dirac 场的动能项。不过无论如何,我们基本没有见过动能项中含有超过两个求导算子的情况。这并不是偶然,因为如果动能项中含有超过两个求导算子,就会造成一种被称为 Ostrogradsky Instability 的现象。 具体来说,就是这样的理论会允许物理系统可以有一直到负无穷的能量。为了理解这一点,我们需要 Hamiltonian。Hamiltonian 是 Lagrangian 经过一个简单的变换生成的,它的主要作用是告诉你这个系统的能量可以取哪些值。举个例子,一个经典的自由粒子的 Hamiltonian 是 p^2/2m ,其中 p 是动量, m 是质量。动量可以从 -\infty 一直取到 +\infty ,此时 Hamiltonian 可以取 [0,+\infty) ,也就告诉你自由粒子的能量一定是 \geqslant0 的。 但是如果你的 Lagrangian 中含有超过两个求导算子,那么我们可以证明,Hamiltonian 会出现如下的形式 H = P_1X_2 + \cdots 其中 P_1 是某种动量(术语上叫广义动量), X_2 是某个坐标。这个时候我们发现如果 P_1 可以随意在 (-\infty,+\infty) 中取值,那么 Hamiltonian 的范围也是 (-\infty,+\infty) 。这就造成了一个严重的问题,如果能量没有下界,那么这个系统(或者其中一部分)就会无止境地向能量较低的状态去演化,从而造成强烈的不稳定性,这是不可接受的。 因此,现在主流的基本理论都只含有两个一下的求导算子。含超过两个求导算子的理论其实也存在,比如用于解决某些特定问题的宇宙学模型。不过在这种情况下,我们会被迫引入一系列约束条件来消除 Ostrogradsky instability。如果你希望你的理论具有一定的普适性,这么做其实得不偿失。不过针对某些特定问题有时候还是有点用。 再来看势能项。势能项只包含我们的动力学变量(比如坐标 x 或者某个场 \varphi(x) ),因此我们可以将其进行展开(类似于微积分里面的 Taylor 展开)。展开之后具有幂级数的形式 V(x) = C_0 + C_1 x + C_2x^2 + C_3 x^3 + \cdots 每一个 x^n 之前都会有一个系数 C_n ,这个系数控制了对应的相互作用的强度。比如,我们知道弹簧系统的势能项是 V(x) = \frac{1}{2}kx^2 这并不意味着其它的项前面的系数都是0,它们可能只是很小,从而使得相应的相互作用很弱因而被忽略。 这个系数的量纲是一个很值得说道的东西。在这之前我们需要知道自然单位制,没见过的同学看文末[1]。在量子场论中,这个系数并不是标准的“常数”,而是一个会随系统能标(可以是系统总能量,或者其中某个实体的能量)而变化的一个量。也就是说,相互作用的强度会随着能标而变化。 如果某个项的系数具有正的质量量纲,比如标量场论中,系数是 m^2/2 ,质量量纲是+2,那么它的强度会随着能标的下降而上升,这种项被称为 relevant;反过来,如果系数具有负的质量量纲,比如引力常量 G ,那么它的强度会随着能标的下降而下降,这种项被称为 irrelevant。而没有量纲的被称为 marginal。 这个事情有什么用呢?通常情况下我们的能标是较低的,至少我们目前还不能做到让一个系统达到任意能标。在较低能标的情况下,所有 relevant 的项具有较高的强度,所有 irrelevant 的项具有较低的强度。因此我们只需要考虑 relevant 的项即可。 在场论中,Lagrangian 的量纲是+4,标量场 \varphi 是+1,因此 \varphi^4 的项就是 marginal 了, \varphi^5 及以上就是 irrelevant 了。于是低能情况下我们只需要考虑至多3个项。这个结论对于很多理论均适用,也即 relevant 的项总是有限个,因此低能下只需要考虑有限个势能项。 所以这是不是意味着我们通常是见不到这些 irrelevant 的项的作用呢?并不是。在高能标下,一切都要倒过来,也即 relevant 项会很弱,而 irrelevant 项很强。要获得高能标,除了注入能量以外还可以注入质量。所以在注入足够多质量以后,我们发现了 irrelevant 项的作用 —— 这就是引力。引力相互作用的系数是引力常量 G ,具有负的质量量纲。 就先讲这么多,希望大家可以感受到现代理论物理工具的强大。通过 theory generators,我们可以高屋建瓴地做一些判断,可以得到一些对许多理论都适用的结论。我们不需要知道Lagrangian 太多的细节,就可以根据 Noether 定理断言守恒量的存在。对于量子场论甚至弦理论这样的 generators 也一样。我们现在对弦理论依然知之甚少,不过已经足以让我们推测量子引力和量子纠缠很可能是一回事(所谓的 ER=EPR)。我们可以对 Lagrangian 进行细致的分析,从而判断出怎样的形式会带来怎样的结果。因此,对于现在的理论物理学家来说,与其说我们是在从现实中寻找规律从而创立理论,不如说我们在尝试设计一些理论。正如我们提到的,Lagrangian 不是可以随便写的,否则就要出问题。这些探索的经验让我们知道,这个自然界之所有有这些规律,这些规律之所以是这些形式,都是有更深层次的原因的。这也是为什么理论物理吸引了如此多的顶级智力为之工作。 [1] 在自然单位制下, c = \hbar = 1 。也就是说,我们把长度单位定义为光在1秒内走过的距离,这样光速的值就是1。这样一来我们有 [\text{time}] = [\text{length}] ,也就是说从量纲角度上讲,长度和时间的量纲是一样的。同理根据 \hbar = 1 我们有 [\text{mass}] = [\text{length}]^{-1} 。这个故事就是告诉你长度,时间,质量三个量纲,现在我们只需要一个,这里我们选质量。 |
|
数学已经发展到不会让普通人震惊的水平了——因为根本看不懂。绝大部分数学论文的题目,对普通人来说每个字都不认识,连在一起更不认识。连论文里研究的基本对象是什么都不知道,连对象具有的某个性质是什么意思都不懂,哪里还会震惊啊。 |

|
|
理论物理已经发展到跟数学一样“艰深晦涩”的水平。但得益于科普,有些论文题目中好歹能遇到一两个媒体反复提到的热词,能够让普通人“望文生义”一下,虽然想当然式的理解与理论物理中实际概念可能是天壤之别,至少表现得比数学“亲民”一点。不过大部分人面对理论物理可能是这个状态: |

|
|
|
|
数学学得不太专业,我只说物理。 丛观整个物理学史,我认为真正令人震惊的不是公式变得有多复杂(地心说搞得也挺复杂的。。。),而是物理学已经越来越脱离直观了。 牛顿时期: 老祖宗牛顿真是开了个好头啊,为了建立物理理论自己先搞出来了微积分,算是数学和物理结合的最初典范,简简单单的三个公式上能预测天体运动下能解释斜坡上的小滑块,真是让人不服不行。 牛顿力学的基本物理量是空间坐标x,时间t,质量m,还有能量,这几个量正常人都能很直观地理解是什么意思,在自然语言中也经常使用。 而且微积分这个东西直观性也非常好,想想我们解高数题的时候用到了很多形象思维,比如说我们可以把微分理解为小量,把积分理解为求和,仔细想想和初等数学差别不大。 后牛顿时期: 牛顿之后就是统计力学,麦克斯韦电磁学,分析力学这些了。虽然这些理论一定程度上独立于牛顿力学,但是和牛顿力学没有根本世界观上的矛盾。而且这些理论需要的数学也不过就是初等数学+微积分。 其中电磁学的基本物理量是电场和磁场,统计力学引入了熵,热这些量,总的来说直观性还是杠杠的。而分析力学比较微妙,虽然理论体系和牛顿力学完全等价,但是却以拉格朗日量和哈密顿量为基本物理量,之所以定义这两个量完全出于数学上的考量,没有直观性。后来证明这兄弟俩在现代物理中发挥了极其重要的作用。 爱因斯坦时期: 自从爱因斯坦降临于世,物理学就开始向变态的方向发展了。。。 在牛顿时期,是先有物理学的直观,然后才发展出了所需要的数学。而爱因斯坦时期恰恰相反,有一些之前数学家随便瞎玩的东西,本来没觉得和现实世界有任何关系,在这一时期却被引入了物理学,具体来说指的是微分流形,群论等。 狭义相对论告诉我们,时间空间地位相当,都是四维时空矢量的分量,切换惯性系实际上是在对四维时空进行旋转,我们可以类比三维旋转来理解。而动量,波矢,电磁场这些物理量都可以找到相应的四维协变形式。 广义相对论告诉我们,时空不是平坦的而是拧在一起的,我们之所以感觉是平坦的完全是因为我们周围没有密度特别大的东西所以时空弯曲效应不明显(当然这是在把地球造成的时空弯曲解释为引力的前提下说的),时间和空间第一次在物理学里发生了如此深刻的关联!真正描述时空的不是欧式几何而是黎曼几何(怒打康德脸)。总的来说,爱因斯坦用微分流形的语言取代了正常人对时空naive的理解,我们发现直观上想当然是对的东西不一定真是对的(如几何学里的平行线公理在现实世界就不对)。不过我们还是可以用可直观的二维三维空间弯曲来理解四维时空的弯曲。除了强调时空几何以外,相对论并没有比牛顿力学多引入任何基本物理量,只是把物理量整理成Lorentz协变的形式。 然后再说量子力学,尽管这家伙用到的数学没有广义相对论复杂,但真是太反直观了。 1. 它沿袭了分析力学里面哈密顿量,广义坐标的概念。 2. 牛顿力学里面用坐标和速度来描述一个粒子的状态,而量子力学不认为一个粒子有确定的坐标和速度,因此用波函数来表征粒子的状态,波函数的模方正是粒子的概率密度分布。除了坐标和动量以外,其他物理量也是概率性的。 3. 量子力学不认为物理量是个数,而是算符,或者说是线性代数里面的线性变换(Hermite的),(所以公式里两个物理量的位置就不能像以前那样按照乘法交换律随意交换),代数第一次在物理学里面被提到这么高的地位! 4. 它用的线性代数还不是大多数本科生学的实数域上的线代,而是复数域上的。没错,量子力学基本方程薛定鄂方程里面含有虚数!和电动力学里那种为了计算方便而引入的虚数不同,量子力学理论本身就需要复数结构!看上去不可能有物理意义的虚数居然出现在基本方程里面,这是何等的疯狂! 量子场论时期: 场论是现代物理的基本语言。其中基本物理量叫做场算符,包括标量场,矢量场和旋量场。Free theory的标量场定义为这样: \hat{\phi}(\vec{x},t)=\int \frac{d^3k}{(2\pi)^3}\frac{1}{\sqrt{2\omega_k}}[e^{ikx}\hat{a}_k^\dagger+e^{-ikx}\hat{a}_k] 。如果说量子力学里面的波函数还可以通过概率密度来建立直观,那现在这个场算符就真的一点直观都没有了(实际上应该理解为一大堆谐振子的叠加,但是这样想对我来说很难受,谁关心谐振子啊。。orz),这样定义的一个很大的好处是它在Lorentz变换下的变换性质和普通的标量场一样。 学狭义相对论的时候我们一般把Lorentz变换理解为一些固定的四维矩阵,但是场论里自旋(spin)的概念让我们认识到,真正最重要的不是那个Lorentz矩阵,而是矩阵背后的Lie代数,或者说是Lorentz群。那个矩阵只不过是Lorentz群的一个四维表示(representation)而已,而像旋量这种二维的东西是按照二维的表示进行变换的。试问在相对论性量子力学建立之前,无论是数学家还是普通人,谁能想到群论这种高度抽象的东西能和自然界有这么深刻的联系? 场论对何谓粒子的理解也是高度抽象的,不是我们平常脑子里想的一个个小球,我引用Schwartz教材里的话: Particles transform under irreducible unitary representations of the Poincare group. This statement can even be interpreted as the definition of what a particle is. 很多人总是好奇反粒子到底是啥东西,其实在场论里,对反粒子的定义也是纯粹抽象的,没人能直观地告诉你为啥存在反粒子。 另外,场论把对称性的重要性提到了前所未有的高度,一个拉格朗日量之所以是其所是的样子,通常就是出于对对称性(包括Lorentz不变性)的考虑。很显然这是一个数学的理由而不是一个直观的理由。 再之后就是弦论,我暂时还不懂就不说了。 总结: 可以说整个物理学史是有从直观向抽象发展的趋势的。数学和物理如此深度的统一,在物理学之外的任何自然科学,社会科学,工科,商科都不曾出现过,这就是理论物理对我来说最令人震惊的地方。基于这个原因,数学和物理的统一体在我心中是人类文明最闪耀的两颗巨星中的一颗。 —————————————————————————————————————— 我昨天发现了一篇讲数学物理关系的一篇文章:《数学与物理桥梁下的鸟瞰》 ,一开篇就讲共形场论和弦论。。反正我是看不懂orz。。如果看我写的这篇答案不过瘾可以继续看他这篇文章。 |
|
我老板是德国人,做微分几何的。他常常提醒我们要多学点微分几何以外的数学,起码要知道不同领域的基本语言;他当初在波恩读PhD的时候,因为德国的教育体制过于追求专业,不同数学方向之间不怎么交流,他基本没学过微分几何以外的数学——比如代数几何。对现代数学有点了解的人应该知道波恩/马普所也算是代数几何和数论的重镇之一吧,我老板就是个在这种地方读博出来的对代数几何一窍不通的数学家。不仅不懂代数几何,他基本也不懂sheaf theory,而且很反感范畴论——他不知道这种语言在他自己领域的研究中有什么用。他做的数学,用数学界的标准来衡量算是非常具体的数学,很大一部分都在构造满足各种曲率条件的度量的例子,有些都能写出显式表达式。 所以我说这些是想表达什么呢?外行人可能以为纯数学只是个小圈子。其实这种想法并不是很准确,不同方向的数学家可能对对方的工作完全不能理解,甚至有时候说是看天书也不过分。这种现象在其他行业好像不是那么普遍,就算有,程度也没这么重吧。做计算机软件和硬件的不至于无法在专业方面沟通吧;不同科室的医生对对方擅长的领域或多或少知道一些基础常识吧。而我老板在代数几何方面基本属于搞不清Zariski topology甚至不一定知道Noether正规化定理的水准。。 所以这就是现代数学发展到的现状。高度精专,不同方向都是隔行如隔山;具体到每个小领域,具体研究的问题,整个世界上可能真的只有十几个人能搞懂证明细节。理论物理其实也差不多。我们系的Ron Donagi教授年年都开数学物理的PhD课。去年我老板心血来潮也想了解这帮搞数学物理的到底在研究些什么,去听了第一节课,以后就再也没去过了。。 |
|
重发个以前写的水文! 现代理论物理学最令人震惊的事实是理论物理学实际上出人意料的简单。你可以在一张餐巾纸上写下整个宇宙的设计。 \begin{align*} S &= \int \mathrm{d}x \sqrt{g} \left [ \frac{1}{G} R + \frac{1}{g^2}F^2 +\bar{\psi}D\mkern-10.5mu/ \psi + (D \varphi) ^2 + V(\varphi) + \bar{\psi}\varphi \psi \right ]\\ Z &= \int \mathscr{D}[field] \Large e^{\large \frac{i}{\hbar}S}\\ \end{align*}\\ 简单解释一下图中符号, S 是我们称之为作用量的东西, R 代表引力场的作用, F^2 代表另外三种相互作用, \psi 代表夸克、轻子场, \varphi 是Higgs标量场, Z 是路径积分。我在这里省略了许多细节性的东西。 上面所写的公式基本上和大多数物理学家认为的差不多,有些物理学家可能会加上超对称性。我们对于物理学的探索可以归结为寻找一个简单的公式。当物理学家梦想在一张餐巾纸上写下关于整个宇宙的全部物理学时,指的是要写下宇宙的作用量。 经典的物理学总是遵循 \delta S = 0 , 大自然喜欢按照最简单的方式运行。 \delta S =0 被叫做最小作用量原理。神奇的量子力学除了 \delta S = 0 所确定的 S_{\textbf{极值}} 路径外,也可以选择其他偏离的路径。这是我们上面第二公式叫做路径积分的原因。 当然上面的公式并不是真正的终极公式。首先 S 的第一项描述万有引力部分 \int \mathrm{d} x \sqrt{g} R 不能和下面的 Z 路径积分相容和;其次剩下的那些项即标准模型部分只是简单的拼凑在一起,并没有真正的统一起来,我们需要三个群 SU(3) 、 SU(2) 、 U(1) , 19个自由的参数微调才能让实验数据和理论相符合。 理论物理学的高级部分和你在高中、大学低年级学到的物理学最主要的区别在于美学的使用。这里以电磁学为例子。最开始的静电学是对牛顿万有引力的模仿,库伦公式 \displaystyle\frac{Q_1Q_2}{r^2} 和万有引力公式 \displaystyle\frac{m_1m_2}{r^2} 一模一样,除了电荷的符号是可正可负,质量的符号总是正的。后来奥斯特偶然发现了电流能产生磁力 \displaystyle\mathrm{d} \mathbf{B} = \frac{I\mathrm{d}\mathbf{l}\times \mathbf{r}}{\mathbf{r}^3} ,到法拉第发现电磁感应现象 \displaystyle\oint_l \mathbf{E}\mathrm{d}\mathbf{l} = - \frac{\mathrm{d}\Phi}{\mathrm{d}t} ,最后天才的麦克斯韦把法拉第关于场的思想数学化,最终完成了电磁学。 麦克斯韦方程组,如下 \begin{align*} & \int\!\!\!\!\!\int_S\mkern-26mu \bigcirc \space\mathbf{E}\cdot \mathrm{d}\mathbf{S} = \iiint_V 4\pi \rho \mathrm{d} V\\ & \int\!\!\!\!\!\int_S\mkern-26mu \bigcirc\space \mathbf{B}\cdot \mathrm{d}\mathbf{S} = 0 \\ & \oint_l \mathbf{E}\cdot\mathrm{d}\mathbf{l} = - \iint_S \frac{\partial \mathbf{B}}{\partial t}\cdot\mathrm{d}\mathbf{S} \\ &\oint_l \mathbf{B}\cdot \mathrm{d}\mathbf{l} = \iint_S 4\pi \mathbf{J}\cdot\mathrm{d}\mathbf{S} + \iint_S \frac{\partial \mathbf{E}}{\partial t} \cdot\mathrm{d} \mathbf{S} \end{align*}\\ 方程组各个方 程排列的顺序大致反映了电磁学发展的过程,人们从发现某些现象开始、不断的探索和实验、最后经由很多人才归纳总结出了物理规律。 麦克斯韦方程组的积分形式在这里不是很方便,我把它改成微分形式 \begin{align*} &\nabla \cdot \mathbf{E}= 4\pi \rho \\ & \nabla \cdot \mathbf{B} = 0 \\ & \nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t} \\ & \nabla \times \mathbf{B} = \frac{\partial \mathbf{E}}{\partial t} + 4\pi \mathbf{J} \end{align*}\\ 我们可以使用一些数学技巧来改写麦克斯韦方程组,注意第二个方程 \nabla \cdot \mathbf{B} = 0 ,根据数学关系 \nabla \cdot (\nabla \times \mathbf{A} )= 0 , 得到 \mathbf{B} = \nabla \times \mathbf{A} ;再将 \mathbf{B} = \nabla \times \mathbf{A} 带入第三个方程,得到 \nabla \times (\mathbf{E} + \frac{\partial \mathbf{A}}{\partial t}) = 0 ,根据数学关系 \nabla \times \nabla \varphi =0 , 得到 \mathbf{E} = - \nabla \varphi - \frac{\partial \mathbf{A}}{\partial t} 。最后让我们把新得到 \mathbf{B} 和 \mathbf{E} 的表达式代入剩余的方程,得到 \begin{align*} &\frac{\partial^2 \varphi}{\partial t^2} - \nabla^2 \varphi -\frac{\partial }{\partial t}(\frac{\partial \varphi}{\partial t} + \nabla \cdot \mathbf{A}) = 4\pi \rho \\ & \frac{\partial^2 \mathbf{A}}{\partial t^2} - \nabla^2 \mathbf{A} + \nabla (\frac{\partial \varphi}{\partial t}+ \nabla \cdot \mathbf{A}) = 4\pi \mathbf{J} \end{align*}\\ \mathbf{B} = \nabla \times \mathbf{A} 和 \mathbf{E} = - \nabla \varphi - \frac{\partial \mathbf{A}}{\partial t} 初看上去非常不一样,但是仔细观察它们的分量 \begin{align*} &B^1 = \frac{\partial A^3}{\partial x^2} - \frac{\partial A^2}{\partial x^3}, \quad E^1 = - \frac{\partial \varphi}{\partial x^1} - \frac{\partial A^1}{\partial t}\\ &B^2 = \frac{\partial A^1}{\partial x^3} - \frac{\partial A^3}{\partial x^1},\quad E^2 = - \frac{\partial \varphi}{\partial x^2} - \frac{\partial A^2}{\partial t}\\ &B^3 = \frac{\partial A^2}{\partial x^1} - \frac{\partial A^1}{\partial x^2}, \quad E^3 = - \frac{\partial \varphi}{\partial x^3} - \frac{\partial A^3}{\partial t} \end{align*} \\ 为了让你看的更清楚,我们引入一些记号 A^{\mu} = (\varphi, \mathbf{A}) = (\varphi, A^1, A^2, A^3) , A_\mu = (\varphi, - \mathbf{A}) = (\varphi, -A^1, - A^2, -A^3) \partial_\mu =(\frac{\partial}{\partial t}, \nabla)= (\frac{\partial}{\partial t}, \frac{\partial}{\partial x^1},\frac{\partial}{\partial x^2},\frac{\partial}{\partial x^3}) , \partial^\mu =(\frac{\partial}{\partial t}, -\nabla)= (\frac{\partial}{\partial t}, -\frac{\partial}{\partial x^1},-\frac{\partial}{\partial x^2},-\frac{\partial}{\partial x^3}) 现在很容易发现 \mathbf{B} 和 \mathbf{E} 的关系 \begin{align*} &B^1 = \partial^3 A^2 - \partial^2 A^3, \quad E^1 = \partial^1 A^0 - \partial^0 A^1\\ &B^2 = \partial^1 A^3 - \partial^3 A^1, \quad E^2 = \partial^2 A^0 - \partial^0 A^2\\ &B^3 = \partial^2 A^1 - \partial^1 A^2, \quad E^3 = \partial^3 A^0 - \partial^0 A^3\\ \end{align*} \\ 我们定义 F^{\mu\nu} := \partial^\mu A^\nu - \partial^\nu A^\mu , \mathbf{B} = (-F^{23},- F^{31},- F^{12}) , \mathbf{E} = (F^{10}, F^{20}, F^{30}) 最终我们发现 \mathbf{B} 和 \mathbf{E} 是矩阵 (F^{\mu\nu}) 的元素 \begin{align*} (F^{\mu\nu}) = \begin{pmatrix} 0 & - E^1 & -E^2 & -E^3 \\ E^1 & 0 & -B^3 & B^2 \\ E^2 & B^3 & 0 & -B^1 \\ E^3 & -B^2 & B^1 & 0 \end{pmatrix} \end{align*} \\ 在我们的新记号下,麦克斯韦方程组的第一个和第四个方程 \begin{align*} &\frac{\partial^2 \varphi}{\partial t^2} - \nabla^2 \varphi -\frac{\partial }{\partial t}(\frac{\partial \varphi}{\partial t} + \nabla \cdot \mathbf{A}) = 4\pi \rho \\ & \frac{\partial^2 \mathbf{A}}{\partial t^2} - \nabla^2 \mathbf{A} + \nabla (\frac{\partial \varphi}{\partial t}+ \nabla \cdot \mathbf{A}) = 4\pi \mathbf{J} \end{align*} \\ 就成一个方程 \Box A^\mu - \partial^\mu(\partial_v A^v) =4\pi J^\mu\\ \Box := \partial_\mu \partial^\mu = \frac{\partial^2}{\partial t^2} - \nabla^2 是达朗贝尔算符, J^\mu := (\rho, \mathbf{J}) 。我们还可以得到更简单的形式,因为 \begin{align*} &\Box A^\mu - \partial^\mu(\partial_\nu A^\nu) =4\pi J^\mu \Rightarrow \partial_\nu \partial^\nu A^\mu -\partial^\mu(\partial_\nu A^\nu) = 4\pi J^\mu \\ &\Rightarrow \partial_\nu(\partial^\nu A^\mu - \partial^\mu A^\nu) = 4\pi J^\mu \Rightarrow \partial_\nu F^{\nu\mu} = 4\pi J^\mu \end{align*} \\ 麦克斯韦方程组的第二个方程 \nabla \cdot \mathbf{B} = 0\\ 我们带入 \mathbf{B} 的新的表示 \partial^1 F^{23} + \partial^2 F^{31} + \partial^3 F^{12} = 0\\ 第三个方程 \nabla \times \mathbf{E}+ \frac{\partial \mathbf{B}}{\partial t} = 0\\ 带入 \mathbf{B} 和 \mathbf{E} ,得到 \begin{align*} & \partial_2 F^{30} - \partial_3 F^{20} - \partial_0 F^{23} =0 \\ & \partial_3 F^{10} - \partial_1 F^{30} - \partial_0 F^{31} =0 \\ & \partial_1 F^{20} - \partial_2 F^{10} - \partial_0 F^{12} =0 \end{align*} \\ 把偏导数的下标调整为上标,并改变排列顺序 \begin{align*} & \partial^2 F^{30} + \partial^3 F^{02} + \partial^0 F^{23} =0 \\ & \partial^3 F^{10} + \partial^1 F^{03} + \partial^0 F^{31} =0 \\ & \partial^1 F^{20} + \partial^2 F^{01} + \partial^0 F^{12} =0 \end{align*} \\ 我们发现麦克斯韦方程组的中间两个方程可以写成 \partial^\mu F^{\nu \rho} + \partial^\nu F^{\rho \mu} + \partial^\rho F^{\mu\nu} = 0\\ 我们为什么要花很大的篇幅来改写麦克斯韦方程组呢?原因是最开始的方程形式并不方便我们理解电磁学的实质,电场 \mathbf{E} 和和磁场 \mathbf{B} 是割裂的,没有一个统一的图像。实际上麦克斯韦方程组完成后就给当时的物理学家带来了巨大的困扰,因为麦克斯韦方程组不符合伽利略的相对论性原理。这个困扰直到1905年才被瑞士伯尔尼专利局的一个小职员解决,你一定听说过这个小职员。我们得到的方程 \begin{align*} & \partial_\mu F^{\mu\nu} = 4\pi J^\nu \\ &\partial^{\mu}F^{\nu \rho} +\partial^{\nu}F^{\rho \mu}+\partial^\rho F^{\mu\nu} = 0 \end{align*} \\ 正是狭义相对论下麦克斯韦方程的张量形式。麦克斯韦方程组更加简洁的形式是 \begin{align*} & \delta F = 4\pi J \\ &\mathrm{d} F = 0 \end{align*} \\ 还有什么更简单的办法来理解电磁场呢?那就是美学的思想,物理学的美通常和对称性联系在一起,现在来介绍这种用美学的思想来建立物理学的方法。 我们知道狭义相对论和量子力学是所有物理学都要遵守的规则,这里暂时把广义相对论放一边。相对论是一个容易让人误解的名词,有点讽刺的是相对论实际上是某种“绝对论”,绝对的东西是什么呢?那就是在所有参考系中,我们对于光速的看法都是一致的。光速的不变性为我们提供一把很好的尺子用来度量时空。利用人类自古巴比伦时代就知道的知识,它在西方被叫做毕达哥拉斯原理在中国叫做勾股原理。我们知道时空中的距离是 s^2 =( x^0)^2 + (x^1)^2+(x^2)^2 +(x^3)^2\\ 有一点特殊的是表示时间的坐标是一个虚数 x^0 = ic t 。对于光子 s^2 = 0 总是成立的,即光速是c。而其它粒子 -(x^0)^2 + (x^1)^2 +(x^2)^2+(x^3)^2\quad(\text{大多数加号})\\ 或者 (x^0)^2 - (x^1)^2 -(x^2)^2 -(x^3)^2 \quad(\text{大多数减号})\\ x^0 = ct 。所有的符合相对论的场都是满足 E^2 - (p^1)^2 -(p^2)^2 -(p^3)^2 = m^2\\ 当和量子力学结合后,狭义相对论下的波动方程失去了非相对论的薛定谔方程 i\hbar \frac{\partial \psi}{\partial t} = \hat{H}\psi\\ 的波函数意义,需要进行二次量子化。 我们回到正题,所有满足狭义相对论的自由场(不参与相互作用)的方程都是类似克莱因-戈登方程 (\Box +m^2)\phi = 0\\ 我们上面的电磁场的波动方程 \Box A^\mu - \partial^\mu(\partial_\nu A^\nu) = 0 \quad(\text{真空无电荷})\\ 可以取洛伦兹规范 \partial_\mu A^\mu = 0\\ 变为 \Box A^\mu = 0 。类似的线性引力场方程 \Box \bar{h}_{\mu\nu} -\partial_\mu \partial^\rho \bar{h}_{\rho\nu} -\partial_\nu \partial^\rho \bar{h}_{\rho \mu} + \partial_\mu \partial_\nu \bar{h}^\rho{}_\rho = 0 \\ 取无迹条件 \eta^{\mu\nu}\bar{h}_{\mu\nu} = 0\\ 和洛伦兹规范 \partial^\mu \bar{h}_{\mu\nu} = 0\\ 得到 \Box \bar{h}_{\mu\nu} = 0\quad(\text{线性引力波})\\ 费米子场方程 (i\partial\mkern-10.5mu/ - m)\psi =0\\ 看上去不是很像,我们乘上 i\partial\mkern-10.5mu/ +m\\ 得到 (\Box +m^2)\psi = 0 打开克莱因-戈登方程 \left [\left (\frac{\partial}{\partial x^0} \right )^2-\left (\frac{\partial}{\partial x^1} \right )^2 -\left (\frac{\partial}{\partial x^2} \right )^2-\left (\frac{\partial}{\partial x^3} \right )^2 +m^2 \right ] \phi =0\\ 对于平面波解 \phi \sim e^{i(Et -\mathbf{p}\cdot \mathbf{x})} ,得到 [-E^2 +(p^1)^2 +(p^2)^2 +(p^3)^2 + m^2]e^{i(Et - \mathbf{p}\cdot \mathbf{x})}=0\\ 恰恰就是 E^2 = \mathbf{p}^2 +m^2 。实际上这些波动方程就是通过 E \rightarrow i\hbar\frac{\partial}{\partial t} , \mathbf{p} = -i\hbar\nabla\\ 替换而构造成的。电磁场除了遵守狭义相对论的不变形式外,还存在一种内部的对称性。 在得到 \mathbf{B} = \nabla \times \mathbf{A}\\ 和 \mathbf{E} = - \nabla \varphi - \frac{\partial \mathbf{A}}{\partial t}\\ 过程中,我们使用了 \nabla \times \nabla \varphi =0\\ 我们可以定义一个新的 \mathbf{A}^\prime = \mathbf{A} + \nabla \phi\\ 新定义下的磁场 \mathbf{B}^\prime = \nabla \times \mathbf{A}^\prime = \nabla \times \mathbf{A} +\nabla \times \nabla \phi= \mathbf{B}\\ 是不变的。要想保持 \mathbf{E}^\prime = -\nabla \varphi^\prime - \frac{\partial \mathbf{A}^\prime}{\partial t}= -\nabla( \varphi -\frac{\partial \phi}{\partial t} )- \nabla \left (\frac{\partial \phi}{\partial t}\right ) - \frac{\partial \mathbf{A}}{\partial t} = \mathbf{E}\\ 是不变的, \varphi^\prime = \varphi - \frac{\partial \phi}{\partial t} 。这样我们便知道 A^\mu 加上任意函数 \partial^\mu\phi ,并不会改变电场和磁场 F^{\mu\nu} 。 A^{\prime \mu} = A^\mu - \partial^\mu \phi 叫做规范变换。让我们来看看电子的场在规范变换 e^{-ie\theta(x)} 下的样子,如下 \begin{align*} \mathcal{L}^\prime &= \bar{\psi}e^{ie\theta(x)}i\gamma^\mu \partial_\mu(e^{-ie\theta(x)}\psi) - m\bar{\psi}\psi \\ &=\bar{\psi}i\gamma^\mu \partial_\mu \psi -m \bar{\psi}\psi - e\bar{\psi}\gamma^\mu\psi\partial_\mu \theta(x)\\ &\neq \bar{\psi}i\gamma^\mu \partial_\mu \psi -m \bar{\psi}\psi = \mathcal{L} \end{align*} \\ 要想消除上式中的 -e\bar{\psi}\gamma^\mu \psi \partial_\mu \theta(x) 。我们可以加上电磁场 A_\mu ,用 D_\mu = \partial_\mu +ieA_\mu 取代普通的偏导数,得到 \begin{align*} \mathcal{L}^\prime &= \bar{\psi}e^{ie\theta(x)}i\gamma^\mu D^\prime_\mu (e^{(-ie\theta(x))}\psi) -m\bar{\psi}\psi \\ & = \bar{\psi}i\gamma^\mu \partial_\mu \psi -m \bar{\psi}\psi - e\bar{\psi}\gamma^\mu\psi(\partial_\mu \theta(x)+A^\prime_\mu) \\ &=\bar{\psi}i\gamma^\mu \partial_\mu \psi -m \bar{\psi}\psi -e\bar{\psi}\gamma^\mu \psi A_\mu \\ &= \bar{\psi}i\gamma^\mu D_\mu\psi - m\bar{\psi}\psi = \mathcal{L} \end{align*} \\ \mathcal{L}^\prime = \mathcal{L} 的关键是 A^{\prime}_\mu = A_\mu -\partial_\mu \theta(x) ,正是我们上面得到的规范变换。我们发现用 D_\mu 取代 \partial_\mu 后,作用量的形式在规范变换下是不变的。和自由场的情况相比唯一的不同是多了一项 -e\bar{\psi}\gamma^\mu\psi A_\mu ,这个就是电子与电磁场的相互作用项 A_\mu J^\mu ,电流 J^\mu 是 -e\bar{\psi}\gamma^\mu\psi (电子带负电荷)。 电子场和电磁场的作用量就是 \begin{align*} \mathcal{L} &=- \frac{1}{4}F_{\mu\nu}F^{\mu\nu} +\bar{\psi}(iD\mkern-10.5mu/ -m)\psi \\ &=\begin{matrix}\\ \underbrace{\color{red}{-\frac{1}{4} F_{\mu\nu}F^{\mu\nu}} } \\ \textbf{电磁场}\end{matrix} +\begin{matrix}\\ \underbrace{\color{blue}{\bar{\psi}(i\partial\mkern-10.5mu/ -m)\psi }} \\ \textbf{电子场}\end{matrix} +\begin{matrix} \textbf{电流}\color{blue}{J^\mu} \\ \underbrace{\overbrace{\color{blue}{-e\bar{\psi}\gamma^\mu\psi}} \color{red}{A_\mu}} \\ \textbf{相互作用项}\end{matrix} \end{align*} \\ 我们将目光转向另一个美丽的理论,广义相对论。广义相对论几乎是由爱因斯坦一个人建立的。 |

|
|
年轻时期的老爱 促成爱因斯坦扩展相对论的动机之一是牛顿引力论和狭义相对论不相容。狭义相对论里有一最大的速度即光速,但是牛顿引力却是超距作用。牛顿引力场方程是 \Delta \phi = 4\pi \rho ,没有时间变化的项。所有满足狭义相对论的场方程都类似于 (\Box + m^2) \phi = 0 ,对于无静质量的场例如电磁场 \Box A^\mu =4 \pi J^\mu 。第二个原因是狭义相对论只对惯性参考系成立,惯性参考系是一种很特殊的参考系,从物理学规律的普适性角度来说需要把狭义相对论拓展到一般参考系。爱因斯坦注意到经典物理学中一个巧合即惯性质量和引力质量成比例。惯性质量是由牛顿第二定律 F = m_Ia 定义的质量,引力质量是万有引力定律 F = - \frac{m_1m_2}{r^2} 定义的,其实引力质量类似于静电学的电荷 。引力质量和惯性质量逻辑上来说是完全不同的两个概念。大家耳熟能详的比萨斜塔实验(有可能伽利略压根没有做过)说在塔顶同时放开两个球,只要初速相同,不管球的质量、成分、大小如何(忽略空气阻力),球必然同时落地。 爱因斯坦发现可以用一个匀加速的参考系来代替均匀的引力场,这便是等效原理。爱因斯坦设计了一个思想实验,有一个以加速度a下落的电梯,电梯外水平方向有一个发光装置。发光装置发出水平方向的光束,电梯里垂直方向有一标尺记录光斑位置。电梯外的观察者看到的光的路径是直线,但是电梯里的人根据标尺记录的光斑的位置却得出光不是直线传播的结论。根据等效原理,均匀引力场的情况下光线的路径也是弯曲的。我们知道光总是走光程最少的路径,真空中光走直线传播。电梯外的观察者的参考系(无加速度)观察到的光的路径是直线,直线是平直空间里最短的路径。反过来说有引力场情况下,因为光线的路径是弯曲的,而光总是走最短的路径,所以时空不是平直时空。一旦知道时空是弯曲的,剩下的就是要寻找能描述弯曲时空的数学。爱因斯坦向大学的同学格拉斯曼寻求帮助,两人发现黎曼开创,里奇和西维塔等人发展起来的流形分析恰好是描述弯曲时空的数学工具。爱因斯坦在格拉斯曼的帮助下,使用黎曼等人开创发展起来的微分几何经过艰辛的努力,花了近10年时间最终完成了广义相对论,找到了引力场方程 R_{\mu\nu} -\frac{1}{2}g_{\mu\nu}R= 8\pi T_{\mu\nu} \\ 广义相对论是物理学里的维纳斯,它是从简单的原理(等效原理)出发,满足美学和物理规律普适性的要求,通过数学方法构造出来的理论。美学上广义相对论无可挑剔,有着漂亮的几何结构,物理规律的普适性上,广义相对论里所有的参考系都是平权的,谁也不比谁优越,物理学规律在所有参考系都有者相同的形式(强等效原理)。 |

|
|
断臂的维纳斯 场方程的左边是纯粹的几何结构,Einstein张量 G_{\mu\nu}:=R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R\\ 在所有黎曼流形上都存在,它是由 \partial \partial = 0 这个拓扑学定理所保证的(详细的讨论参见MTW的巨著《Gravitation》15章BIANCHI IDENTITIES AND THE BOUNDARY OF A BOUNDARY)。由比安基第二恒等式 R^{\alpha}{}_{\beta[\gamma\delta;\epsilon]} = 0\\ 可以诱导出 (R^{\mu\nu} - \frac{1}{2}g^{\mu\nu}R)_{;\nu} = 0\\ 狭义相对论的能量守恒定律 T^{\mu\nu}{}_{,\nu} = 0\\ 推广到一般时空是 T^{\mu\nu}{}_{;\nu} = 0\\ 两相比较得到 R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R+\Lambda g_{\mu\nu} = \kappa T_{\mu\nu}\\ 把 \Lambda g_{\mu\nu} 吸收到 T_{\mu\nu} 中去(原因后面再讲)。你会发现几何学几乎完全决定了方程的形式,除了常数 \kappa 没有确定。要得到 \kappa ,要把场方程退化到牛顿引力场。由牛顿第二定律 \ddot{\mathbf{r}} = - \nabla \phi\\ 分量是 \displaystyle\frac{\mathrm{d}^2 x^i}{\mathrm{d}t^2} = - \partial_i \phi\\ 和广义相对论里的测地线方程 \displaystyle\frac{\mathrm{d}^2x^\mu}{\mathrm{d}\tau^2}+\Gamma^{\mu}{}_{\nu\rho}\frac{\mathrm{d}x^\nu}{\mathrm{d}\tau}\frac{\mathrm{d}x^\rho}{\mathrm{d}\tau} = 0\\ 比较,使用弱场近似得到 \Gamma^i{}_{00} = \partial_i \phi,\quad R_{00} = \partial_i \Gamma^i{}_{00} = \Delta \phi\\ Einstein方程化为 \Delta \phi = \frac{1}{2}\kappa \rho\\ 和牛顿引力场方程 \Delta \phi = 4\pi \rho\\ 比较,得到 \kappa = 8\pi 。通过场方程,比安基第二恒等式保证能量守恒定律是自动成立的。 和方程左边的简洁性相比,方程的右边 T_{\mu\nu} 称之为能量-动量-应力张量的东西让人一言难尽,不同的物质有着不同的形式。例如电磁场的能量动量应力张量是 \frac{1}{4\pi}(F_{\mu\rho}F_{\nu}{}^\rho - \frac{1}{4}g_{\mu\nu}F_{\rho\sigma}F^{\rho\sigma})\\ 标量场的是 \partial_\mu \phi \partial_\nu\phi - \frac{1}{2}g_{\mu\nu}(\partial_\rho\phi \partial^\rho\phi +m^2\phi^2)\\ 理想流体是 (\rho +p)u_\mu u_\nu + pg_{\mu\nu}\\ 对于场方程右边的美学上的不满意把爱因斯坦导向了统一场论之路,爱因斯坦想要像广义相对论一样用美妙的几何学把引力场和电磁场统一起来(那时候还不知道弱力和强力),但是这几乎是不可能完成的任务。 |

|
|
老爱的最后 20 年远离主流物理学,投入到统一场论的宏伟蓝图中,不过没能复刻广义相对论的奇迹。今天爱因斯坦的精神被弦理论学家所继承! 要想理解广义相对论,你必须首先搞明白张量的概念。在本文中你已经不止一次见过它。比如 A^\mu 和 A_\mu , \partial_\mu 和 \partial^\mu , F^{\mu\nu} 和 J^\mu 等等。张量可以简化物理学的方程和公式,正如上面我们所演示的。你也许注意到我们写的叫做张量的量都带有上标或下标,但是并不是带有上标或下标的量都是张量,必须满足一定的法则。就物理学来说,我们希望写下的方程和公式能够有普适性和不变性。我们可以从这方面来理解张量,张量是在坐标变换下不变的量 \mathbf{T} =\overbrace{ \sum_{a_1} \ldots \sum_{b_n} }^{\text{m+n个}}T^{a_1...a_m}_{b_1...b_n} \overbrace{ \partial_{a_1}\otimes\ldots\otimes \partial_{a_m}}^{\text{m个}}\otimes \underbrace{ \\ \mathrm{d}x^{b_1}\otimes\ldots\otimes \mathrm{d}x^{b_n}}_{\text{n个}}\\ 我们可以省略掉求和号因为 T^{...a...} 里面每出现一个上标 a ,必定有一个下标 a 出现在 \partial \otimes \ldots \otimes \partial 中,同样的 T_{...b...} 里面每出现一个下标 b ,必定有一个上标 b 出现在 \mathrm{d}x \otimes \ldots \otimes \mathrm{d}x 中,重复指标求和是爱因斯坦最先使用的,所以也叫爱因斯坦约定。张量 \mathbf{T} 如下,我们加了一些说明 \mathbf{T} =T^{a_1...a_m}_{b_1...b_n} \overbrace{ \partial_{a_1}\otimes\ldots\otimes \partial_{a_m}}^{\text{m个}}\otimes \underbrace{ \\ \mathrm{d}x^{b_1}\otimes\ldots\otimes \mathrm{d}x^{b_n}}_{\text{n个}}\\ 我们可以进行坐标变换 x \to x^\prime , \frac{\partial}{\partial x^{\prime\mu}} = \frac{\partial x^\nu}{\partial x^{\prime\mu}}\frac{\partial}{\partial x^\nu} , \mathrm{d}x^{\prime \mu} = \frac{\partial x^{\prime \mu}}{\partial x^\nu} \mathrm{d}x^\nu 。你会发现 \partial 按 \frac{\partial x}{\partial x^\prime} 这样变换, dx 按 \frac{\partial x^\prime}{\partial x} 变换,一共有 m 个 \frac{\partial x}{\partial x^\prime} 和 n 个 \frac{\partial x^\prime}{\partial x} ,要想保持 \mathbf{T} 不变, \mathbf{T} 必须按 m 个 \frac{\partial x^\prime}{\partial x} ,n 个 \frac{\partial x}{\partial x^\prime} 这样变换, 具体请看 \begin{align*} \mathbf{T} &=T^{\prime a^\prime_1...a^\prime_m}_{b^\prime_1...b^\prime_n} \overbrace{ \partial^{\prime}_{a^\prime_1}\otimes\ldots\otimes \partial^{\prime}_{a^\prime_m}}^{m\text{个}}\otimes \underbrace{ \mathrm{d}x^{\prime b^\prime_1}\otimes\ldots\otimes \mathrm{d}x^{\prime b^\prime_n}}_{n\text{个}} \\ & ={\color{red}{ \underbrace{ \frac{\partial x^{\prime a^\prime_1}}{\partial x^{a_1}}\ldots \frac{\partial x^{\prime a^\prime_m}}{\partial x^{a_m}} }_{\text{m个要抵消下面}\partial\text{ 的变换}} }} T^{ a_1...a_m}_{b_1...b_n} \color{blue}{\overbrace{ \frac{\partial x^{ b_1}}{\partial x^{\prime b^{\prime}_{1}}}\ldots\frac{\partial x^{b_n}}{\partial x^{\prime b^{\prime}_n}}}^{\text{n个要抵消下面}\mathrm{d}x\text{的变换}}}\\ & \qquad \color{red}{\overbrace{ \frac{\partial x^{ a_1}}{\partial x^{\prime a^{\prime}_1}}\ldots\frac{\partial x^{a_m}}{\partial x^{\prime a^{\prime}_m}}}^{\text{m个来自}\partial\text{的变换}}} \color{blue}{\underbrace{ \frac{\partial x^{\prime b^{\prime}_1}}{\partial x^{ b_{1}}}\ldots\frac{\partial x^{\prime b^{\prime}_n}}{\partial x^{b_n}}}_{\text{n个来自}\mathrm{d}x\text{的变换}}} \\ &\qquad \overbrace{ \partial_{a_1}\otimes\ldots\otimes \partial_{a_m}}^{m\text{个}}\otimes \underbrace{\mathrm{d}x^{b_1}\otimes\ldots\otimes \mathrm{d}x^{b_n}}_{n\text{个}}\\ &=T^{a_1...a_m}_{b_1...b_n} \overbrace{ \partial_{a_1}\otimes\ldots\otimes \partial_{a_m}}^{m\text{个}}\otimes \underbrace{ \mathrm{d}x^{b_1}\otimes\ldots\otimes \mathrm{d}x^{b_n}}_{n\text{个}} \end{align*} \\ 我们可以使用分量 T^{a_1...a_m}_{b_1...b_n} 来代替完整的张量形式只需记住分量是按 m 个 \frac{\partial x^\prime}{\partial x} ,n 个 \frac{\partial x}{\partial x^\prime} 变换的。根据 \partial 和 \mathrm{d}x 的数量,来区分张量的类型, \mathbf{T} 叫做 \begin{pmatrix}m\\ n\end{pmatrix} 型混合张量,全是 \partial 的我们叫做逆变张量,全是 \mathrm{d}x 的叫做协变张量。张量的普通微分并不是张量,原因是它不满足我们上面形式。我们可以使用类似电磁场的方法 D_\mu = \partial_\mu +ie A_\mu ,用新的协变微分 \nabla 代替普通的微分 \mathrm{d} ,要求 \nabla \mathbf{T} 也是一个张量,当 \nabla 作用在分量 T 时就像普通微分一样;当 \nabla 作用于 \partial 时,产生一个 \Gamma ;当 \nabla 作用于 \mathrm{d}x ,产生一个 -\Gamma 。 \Gamma 类似于 A 的作用,用来补偿普通微分作用于分量 T 变换时带来的变化。我们可以把 \nabla 当作一个生产 \Gamma 的机器,张量 \mathbf{T} 是一个工厂, \partial 和 \mathrm{d}x 是原材料,分量 T 是指导生产的手册 \partial \otimes \ldots\otimes \mathrm{d}x 是流水线。 下面是 \nabla 机器在张量工厂 \mathbf{T} 生产的过程 \begin{align*} \nabla \mathbf{T} &= \partial_{\color{red}{\star}} T^{a_1...a_m}_{b_1...b_n} \overbrace{\partial_{a_1} \otimes \ldots \otimes \partial_{a_m}}^{\textbf{m个}}\otimes \underbrace{\mathrm{d}x^{b_1}\otimes\ldots \otimes \mathrm{d}x^{b_n}}_{n个}\otimes \color{red}{\mathrm{d}x^{\star}} \\ & +T^{\overbrace{a_1..{\color{green}{a_i}}..a_m}^{\text{指}{\color{green}{\Downarrow}}\text{令}}}_{b_1...b_n} \overbrace{\partial_{a_1} \otimes \ldots \otimes\underbrace{\color{green}{ (\Gamma^{\bullet}{}_{a_i\color{red}\star})} \otimes\partial_{{\color{green}{\bullet}}}}_{(\nabla\partial){\color{green}{\Uparrow}} \Longrightarrow}\otimes\ldots\otimes \partial_{a_m}}^{\partial \text{流水线,方向 }a_1\Longrightarrow a_m,\text{ 机器位置}{\color{green}{\Uparrow}}, \text{生产m个}\Gamma} \otimes\underbrace{\mathrm{d}x^{b_1}\otimes\ldots \otimes \mathrm{d}x^{b_n}}_{n个}\otimes\color{red}{\mathrm{d}x^{\star}}\\ &+T^{a_1...a_m}_{\underbrace{b_1..{\color{blue}{b_j}}..b_n}_{\text{指}{\color{blue}{\Uparrow}}\text{令}}} \overbrace{\partial_{a_1} \otimes \ldots \otimes \partial_{a_m}}^{\textbf{m个}}\otimes \underbrace{\mathrm{d}x^{b_1}\otimes\ldots \otimes \overbrace{ \color{blue}{(-\Gamma^{b_j}{}_{\bullet\color{red}{\star}})}\otimes \mathrm{d}x^{\color{blue}{\bullet}}}^{(\nabla \mathrm{d}x){\color{blue}{\Downarrow}}\Longrightarrow} \otimes\ldots \otimes \mathrm{d}x^{b_n}}_{\mathrm{d}x\text{流水线,方向}b_1\Longrightarrow b_n,\text{机器位置} \color{blue}{\Downarrow},\text{生产n个}-\Gamma}\otimes\color{red}{\mathrm{d}x^{\star}} \\ & =\left (\underbrace{{\color{red}{\partial_{\star}}}T^{a_1...a_m}_{b_1...b_n} +\overbrace{\color{green}{\Gamma^{a_i}{}_{\bullet\color{red}\star}} T^{a_1..\color{green}{\bullet}..a_m}_{b_1...b_n}}^{\text{m个}} -\overbrace{\color{blue}{\Gamma^{\bullet}{}_{b_j\color{red}{\star}}} T^{a_1...a_m}_{b_1..\color{blue}{\bullet}..b_n}}^{\text{n个}}}_{\text{最终的产品,T分量的变换规则}}\right )\\ &\qquad \overbrace{\partial_{a_1} \otimes \ldots \otimes \partial_{a_m}}^{\text{m个}}\otimes \underbrace{\mathrm{d}x^{b_1}\otimes\ldots \otimes \mathrm{d}x^{b_n}\otimes\color{red}{\mathrm{d}x^{\star}} }_{n+1\text{个}} \end{align*} 观察上面的公式,你会发现 \nabla \mathbf{T} 是 \begin{pmatrix} m \\ n +1\end{pmatrix} 型张量,就物理学上的要求来说,我们希望不要改变张量的类型, 最好能消掉多出来的 \mathrm{d}x 。你应该发现 \partial 和 \mathrm{d}x 和你大学学过的微分的公式一样 \mathrm{d}f = \frac{\partial f}{\partial x^i}\mathrm{d}x^i , 我们使用 :=\partial_i f"><\partial_i,df>:=\partial_i f ,这样当 f=x^j 时, =\delta^j_i"><\partial_i, dx^j>=\delta^j_i , i=j 时 \delta 的值为 1,其它情况为 0。 我们可以使用 X:=X^a\partial_a 通过 "><\bullet,\bullet> 来消除额外的 \mathrm{d}x ,这样可以定义一个新的张量 "><\mathbf{X}, \nabla \mathbf{T}> , 这个张量记做 \nabla_{\mathbf{X}}\mathbf{T} 和 \mathbf{T} 是同一类型的张量, \nabla_{\mathbf{X}} 是一台保证张量类型不变的机器。 \nabla_{\mathbf{X}} 将在我们接下来的讨论占据重要位置。 广义相对论一个美好的地方就是物理学规律在所有参考系里都是相同的。我们知道在惯性参考系中,光在真空中传播是走直线的。通过前面的爱因斯坦电梯实验,我们知道在加速参考系里光线是弯曲的。如果光走直线是一条物理规律,那么加速参考系中光线弯曲岂不是和我们所说的物理学规律在所有参考系这个说法相矛盾吗?要解决这个矛盾,我们必须搞清楚什么是直线? 我们这里举一个好玩的例子来说明什么是直线。 有一个二维的圆盘世界,一群二维生物生活在圆盘里。为了叙述方便,我们把它们称为“人”,借用现实世界的人名来区分二维世界的生物。按照讲故事的套路,很久很久以前,圆盘里有一位贤人叫欧几里德发现圆盘里的几何最后可以归结为五条公理,前四条公理都好理解,但是最后一条公理有点复杂,那就是在圆盘世界里过直线外的点可以做无数条直线和这个直线平行(不相交)。圆盘里的数学家都想证明第五条公理和前四条公理不是独立的。他们尝试了很多种方法,都不能证明第五公设。圆盘里的时间慢慢过去了2000年,有一个叫鲍耶的年轻人发现了一种新的几何叫做平面几何,在平面几何里,过直线外一点只能做一条直线和这个直线平行。鲍耶怀着激动的心情找到圆盘世界里的数学权威高斯,希望得到高斯的认可,高斯听了鲍耶的关于新几何的介绍,淡淡回复说这个平面几何其实他二十前就发现了。鲍耶郁闷的离去,整个圆盘里的数学家没有人理他,最后鲍耶郁郁而终。又过了很多年,有一个叫罗巴切夫斯基的数学家也发现了平面几何,圆盘世界的人们这才慢慢发现了鲍耶发现的价值。圆盘世界高斯的学生黎曼发现除了平面几何之外,还有一种几何过直线外一点找不到不相交的直线,叫做球面几何。黎曼总结了前人的成果并加以推广,提出了黎曼几何。圆盘里的物理学家洛伦兹发现越靠近圆盘边缘,长度在缩短,但是圆盘里的人们感觉不到这种变化,因为同样的尺子也在变短,他提出的圆盘世界的洛伦兹变换。最后圆盘世界里的一个年轻人爱因斯坦发现了圆盘里的相对论,并且通过方程发现圆盘世界的几何其实共形于平面几何,圆盘世界是个负的二维常曲率空间。我们例子里的圆盘世界是著名的庞加莱圆盘,和圆盘边界垂直的圆弧是圆盘世界里的直线。圆盘世界里的三角形内角和小于180度。 |

|
|
庞加莱圆盘的例子是为了让你知道直线并不如你肉眼所见的那样直观而是依赖于背后的几何。在加速参考系中的“直线”其实弯曲的。广义相对论里的“直线”可以用 \nabla_{\mathbf{X}}\mathbf{X}=0 来定义的, \mathbf{X} 是沿着曲线 x^\mu(\tau) 的切矢量场,根据上面的张量公式得到 \begin{align*} \nabla_{\mathbf{X}}\mathbf{X} = \frac{\mathrm{d}^2x^\mu}{\mathrm{d}\tau^2} +\Gamma^{\mu}{}_{\nu\rho} \frac{\mathrm{d}x^\nu}{\mathrm{d}\tau} \frac{\mathrm{d}x^\rho}{\mathrm{d}\tau} =0 \end{align*}\\ 物理学上它表示一个自由下落物体的时空曲线。牛顿力学里的直线是不受力的物体的运动轨迹 \begin{align*} \frac{\mathrm{d}^2x^i}{\mathrm{d}t^2} = 0 \end{align*}\\ 我们把 \begin{align*} \nabla_{\mathbf{X}}\mathbf{X} = 0 \end{align*}\\ 写成物理学家常用的形式 \begin{align*} \frac{\mathrm{D}^2x^\mu}{\mathrm{d}\tau^2} = 0 \end{align*}\\ 你会发现"直线"的规律仍然相同。使用 \nabla_{\mathbf{X}} 可以构造两个很重要的张量 \mathbf{T} 挠率,完整形式如下 \begin{align*} \mathbf{T}= T^a{}_{bc}\partial_a\otimes\mathrm{d}x^b\otimes\mathrm{d}x^c \end{align*}\\ 通过下式 \begin{align*} \mathbf{T}(\mathbf{X},\mathbf{Y}):=\nabla_{\mathbf{X}}\mathbf{Y}-\nabla_{\mathbf{Y}}\mathbf{X}-[\mathbf{X},\mathbf{Y}] \end{align*}\\ 定义和 \mathbf{R} 曲率,完整形式如下 \begin{align*} \mathbf{R}=R^a{}_{bcd}\partial_a\otimes\mathrm{d}x^b\otimes\mathrm{d}x^c\otimes\mathrm{d}x^d \end{align*}\\ 通过下式 \begin{align*} \mathbf{R}(\mathbf{X},\mathbf{Y}):=[\nabla_{\mathbf{X}},\nabla_{\mathbf{Y}}]-\nabla_{[\mathbf{X},\mathbf{Y}]} \end{align*}\\ 定义。我们可以计算得到 \mathbf{R} 的分量 R^a{}_{bcd} ,把 \mathbf{R}(\mathbf{X},\mathbf{Y}) 作用于 \mathbf{Z} 上 \begin{align*} \mathbf{R}(\color{red}{\mathbf{X}},\color{blue}{\mathbf{Y}})\color{green}{\mathbf{Z} } &=\nabla_{\color{red}{\mathbf{X}}}\nabla_{\color{blue}{\mathbf{Y}}}{\color{green}{\mathbf{Z}}}-\nabla_{\color{blue}{\mathbf{Y}}}\nabla_{\color{red}{\mathbf{X}}}{\color{green}{\mathbf{Z}}} -\nabla_{[\color{red}{\mathbf{X}},\color{blue}{\mathbf{Y}}]}\color{green}{\mathbf{Z}} \\ & = \color{red}{X^a\partial_a[\color{blue}{Y^b(\partial_b\color{green}Z^{\color{green}c}+\Gamma^{\color{green}c}{}_{bd} \color{green}Z^d)}]}\color{green}{\partial_c}\\ &\quad+\color{red}{X^a\Gamma^{\color{green}c}{}_{a\color{blue}e}[\color{blue}{Y^b(\partial_b\color{green}Z^e+\Gamma^{e}{}_{bd} \color{green}Z^d)}]}\color{green}{\partial_c}\\ &\quad-\color{blue}{Y^b\partial_b[\color{red}{X^a(\partial_a\color{green}Z^{\color{green}c}+\Gamma^{\color{green}c}{}_{ad} \color{green}Z^d)}]}\color{green}{\partial_c}\\ &\quad-\color{blue}{Y^b\Gamma^{\color{green}c}{}_{b\color{red}e}[\color{red}{X^a(\partial_a\color{green}Z^e+\Gamma^{e}{}_{ad} \color{green}Z^d)}]}\color{green}{\partial_c}\\ &\quad-[X,Y]^b(\partial_bZ^c+\Gamma^{c}{}_{bd}Z^d)\partial_c\\\end{align*} \begin{align*} &\quad\qquad\qquad=\overbrace{\color{red}{X^a\partial_a}\color{blue}{Y^b(\partial_b\color{green}{Z^c}+\Gamma^{c}{}_{bd} \color{green}Z^d)} \color{green}{\partial_c}}^{(\mathbf{X}Y)^b\nabla_b\mathbf{Z}(卒)}\\ &\qquad\qquad\qquad+\overbrace{\color{red}{X^a}\color{blue}{Y^b}(\color{red}{\partial_a}\color{blue}{\partial_b}\color{green}{Z^c} +\color{red}{\Gamma^{\color{green}c}{}_{a\color{blue}e}} \color{blue}{\partial_b\color{green}Z^e}+\color{blue}{\Gamma^{\color{green}c}{}_{bd}\color{red}{\partial_a}\color{green}Z^d})\color{green}{\partial_c}}^{\color{brown}正(亡)}\\ &\qquad\qquad\qquad+\overbrace{(\color{red}{\partial_a}\color{blue}{\Gamma^{\color{green}c}{}_{bd}}+\color{red}{\Gamma^{\color{green}c}{}_{a\color{blue}e}}\color{blue}{\Gamma^{e}{}_{bd}})\color{red}{X^a}\color{blue}{Y^b}\color{green}Z^{\color{blue}d}\color{green}{\partial_c}}^{\color{red}活} \end{align*} \begin{align*}&\qquad\qquad\qquad\overbrace{-\color{blue}{Y^a\partial_a}\color{red}{X^b(\partial_b\color{green}{Z^c}+\Gamma^{c}{}_{bd} \color{green}Z^d)}\color{green}{\partial_c}}^{-(\mathbf{Y}X)^b\nabla_b\mathbf{Z}(卒)}\\ &\qquad\qquad\qquad\overbrace{-\color{red}{X^a}\color{blue}{Y^b}(\color{red}{\partial_a}\color{blue}{\partial_b}\color{green}{Z^c} +\color{red}{\Gamma^{\color{green}c}{}_{ad}}\color{blue}{\partial_b\color{green}Z^{\color{red}d}} +\color{blue}{\Gamma^{\color{green}c}{}_{b\color{red}e}}\color{red}{\partial_a}\color{green}Z^{\color{red}e})\color{green}{\partial_c}}^{\color{brown}负(亡)}\\ &\qquad\qquad\qquad\overbrace{-(\color{blue}{\partial_b}\color{red}{\Gamma^{\color{green}c}{}_{ad}}+\color{blue}{\Gamma^{\color{green}c}{}_{b\color{red}e}}\color{red}{\Gamma^{e}{}_{ad}})\color{red}{X^a}\color{blue}{Y^b}\color{green}Z^{\color{red}d}\color{green}{\partial_c}}^{\color{red}活} \\ &\qquad\qquad\qquad\overbrace{-[X,Y]^b(\partial_bZ^c+\Gamma^{c}{}_{bd}Z^d)\partial_c}^{卒} \end{align*} 换个行(达到知乎latex公式编辑器的长度限制了) \begin{align*} \mathbf{R}(\color{red}{\mathbf{X}}, \color{blue}{\mathbf{Y}})\color{green}{\mathbf{Z}} =(\color{red}{ \partial_a}\color{blue}{\Gamma^{\color{green}c}{}_{b\color{black}d}} -\color{blue}{\partial_b}\color{red}{\Gamma^{\color{green}c}{}_{a\color{black}d}} +\color{red}{\Gamma^{\color{green}c}{}_{a\color{blue}e}}\color{blue}{\Gamma^{e}{}_{b\color{black}d}} -\color{blue}{\Gamma^{\color{green}c}{}_{b\color{red}e}}\color{red}{\Gamma^{e}{}_{a\color{black}d}}) \color{red}{X^a}\color{blue}{Y^b}\color{green}{Z^{\color{black}d}}\color{green}{\partial_c} \end{align*} R^a{}_{bcd}=\partial_c\Gamma^{a}{}_{bd}-\partial_d\Gamma^{a}{}_{bc}+\Gamma^{a}{}_{ec}\Gamma^{e}{}_{bd}-\Gamma^{a}{}_{ed}\Gamma^{e}{}_{bc} 是曲率张量在坐标基下的分量, 即 \mathbf{R}(\mathrm{d}x^a, \partial_b,\partial_c,\partial_d) 。 同样的,得到 \begin{align*} \mathbf{T}(\mathbf{X},\mathbf{Y}) &= \nabla_{\mathbf{X}}\mathbf{Y}-\nabla_{\mathbf{Y}}\mathbf{X} -[\mathbf{X},\mathbf{Y}]\\ &=X^a(\partial_aY^b+\Gamma^b{}_{ac}Y^c)\partial_b-Y^b(\partial_bX^a+\Gamma^a{}_{bc}X^c)\partial_a\\ &\quad-(X^a\partial_aY^b-Y^a\partial_aX^b)\partial_b\\ &=(\Gamma^{c}{}_{ab}-\Gamma^{c}{}_{ba})X^aY^b\partial_c \end{align*} \\ T^c{}_{ab} = \Gamma^{c}{}_{ab}-\Gamma^{c}{}_{ba} 是挠率张量在坐标基下的分量, 即 \mathbf{T}(\mathrm{d} x^c,\partial_a,\partial_b) 。 \nabla_{\mathbf{X}} 、 \mathbf{R}(\mathbf{X},\mathbf{Y}) 和 \mathbf{T}(\mathbf{X},\mathbf{Y}) 都是数学家喜欢使用的抽象符号,它适用于任何仿射几何。物理学里的时空几何是一种度量几何,也就是说存在距离的概念。我们之前说狭义相对论里,自由粒子在时空中运动的距离是 \mathrm{d}s^2= -(\mathrm{d}x^0)^2+(\mathrm{d}x^1)^2+(\mathrm{d}x^2)^2+(\mathrm{d}x^3)^2\\ 广义相对论里是 \mathrm{d}s^2 = \mathbf{g}=g_{\mu\nu}\mathrm{d}x^\mu\otimes\mathrm{d}x^\nu\\ 使用 \mathbf{g} 可以把逆变矢量( X^a\partial_a )和协变矢量( Y_b\mathrm{d}x^b )等同起来。比如你有时看到这样的爱因斯坦方程 R^{\mu\nu}-\frac{1}{2}g^{\mu\nu}R=8\pi T^{\mu\nu}\\ 有时看到是 R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R=8\pi T_{\mu\nu}\\ 这些写法都是正确的,并不会影响它的物理意义。使用 \mathbf{g} 还定义一个新的 \Gamma ,使得挠率消失。这样的 \Gamma 就是无挠联络 \Gamma^c{}_{ab}=\frac{1}{2}g^{cd}(\partial_{a}g_{db}+\partial_{b}g_{ad}-\partial_dg_{ab})\\ 这样的联络是唯一的,同时关于 \mathbf{g} 的协变微分为 0,即 \nabla\mathbf{g} = 0 或 g_{ab;c} = 0 。 以上就是广义相对论使用的优雅、美丽、稍稍有点抽象称之为微分几何的数学,和大多数人印象中的初等几何(就是你在初中和高中学到的)不同,我们并不需要做图、画辅助线、证明各种命题。有下面几个概念被推广到微分几何中,勾股定理(毕达哥拉斯定理)对应于 \mathbf{g} 或 \mathrm{d}s^2=g_{\mu\nu}\mathrm{d}x^\mu\otimes\mathrm{d}x^\nu ,直线对应于 \nabla_{\mathbf{X}}\mathbf{X}=0 ,广义相对论的灵魂蕴含在 \mathbf{R} 中,和狭义相对论的空架子相比, R^{a}{}_{bcd} 不全为0的时空才是灵动的、好玩的,你会在这里面发现黑洞、虫洞、白洞等魔幻的让人着迷的玩意儿,你也会发现Godel的神奇旋转宇宙,甚至是M理论里各种高维的延展体。所有这些都只需要 \mathbf{g} 、 \nabla_{\mathbf{X}} 、 \mathbf{R} ,可能需要 \mathbf{T} (超引力的引力微子场可以当作挠率),而这些量在所有维度都有着相同的形式,要扩展到高维度,只需要把指标取值扩大到相应的维度。我们列出下列关系作为广义相对论的总结。 下图是网络上经常用来吓唬人的标准模型作用量展开式,一大坨冗长枯燥的数学公式很符合大众对于物理学的成见 \begin{align*} \mathcal{L}_{SM} &=-\frac{1}{2}\partial_\nu g^a_\mu \partial_\nu g^a_\mu -g_s f^{abc}\partial_\mu g^a_\nu g^b_\mu g^c_\nu -\frac{1}{4}g_s^2f^{abc}f^{ade}g^b_\mu g^c_\nu g^d_\nu g^e_\nu\\ &\quad - \partial_\nu W^+\partial_\nu W^- -M^2 W^+_\mu W^-_\mu \\ &\quad-\frac{1}{2}\partial_\nu Z^0_\mu \partial_\nu Z^0_\mu -\frac{1}{2c^2_w}M^2 Z^0_\mu Z^0_\mu \\ &\quad-\frac{1}{2}\partial_\mu A_\nu \partial_\mu A_\nu \\ &\quad -igc_w\Big[\partial_\nu Z^0_\mu(W^+_\mu W^-_\nu -W^+_\nu W^-_\mu) -Z^0_\nu(W^+_\mu \partial_\nu W^-_\mu -W^-_\mu \partial_\nu W^+_\mu)\\ &\qquad\qquad +Z^0_\mu(W^+_\nu \partial_\nu W^-_\mu -W^-_\nu \partial_\nu W^+_\mu)\Big] \\ &\quad -igs_w\Big[ \partial_\nu A_\mu (W^+_\mu W^-_\nu - W^+_\nu W^-_\mu) - A_\nu(W^+_\mu \partial_\nu W^-_\mu - W^-_\mu \partial_\nu W^+_\mu) \\ &\qquad\qquad + A_\mu(W^+_\nu \partial_\nu W^-_\mu - W^-_\nu \partial_\nu W^+_\mu)\Big]\\ &\quad-\frac{1}{2}g^2W^+_\mu W^-_\mu W^+_\nu W^-_\nu +\frac{1}{2}g^2W^+_\mu W^-_\nu W^+_\mu W^-_\nu\\ &\quad +g^2c^2_w(Z^0_\mu W^+_\mu Z^0_\nu W^-_\nu - Z^0_\mu Z^0_\mu W^+_\nu W^-_\nu)\\ &\quad + g^2s^2_w(A_\mu W^+_\mu A_\nu W^-_\nu -A_\mu A_\mu W^+_\nu W^-_\nu)\\ &\quad + g^2s_wc_w\Big[A_\mu Z^0_\nu(W^+_\mu W^-_\nu - W^+_\nu W^-_\mu)-2A_\mu Z^0_\mu W^+_\nu W^-_\nu \Big]\\\end{align*} \begin{align*} \qquad&\quad-\frac{1}{2}\partial_\mu H \partial_\mu H -\frac{1}{2}m_h^2 H^2 \\ &\quad-\partial_\mu \phi^+ \partial_\mu \phi^+ -M^2\phi^+\phi^- \\ &\quad-\frac{1}{2}\partial_\mu \phi^0 \partial_\mu \phi^0 -\frac{1}{2c^2_w}M^2 \phi^0\phi^0\\ &\quad - \beta_h \Big[\frac{2M^2}{g^2}+\frac{2M}{g}H+\frac{1}{2}(H^2+\phi^0\phi^0+2\phi^+\phi^-)\Big]\\ &\quad+\frac{2M^4}{g^2}\alpha_h -g\alpha_h M(H^3+H\phi^0 \phi^0 +2H\phi^+\phi^-)\\ &\quad-\frac{1}{8}g^2\alpha_h \Big[H^4 + (\phi^0)^4 +4(\phi^+\phi^-)^2 + 4(\phi^0)^2\phi^+\phi^- \\ &\qquad\qquad\qquad+ 4H^2\phi^+\phi^- + 2(\phi^0)^2 H^2\Big]\\ &\quad - gM W^+_\mu W^-_\mu H -\frac{1}{2}g\frac{M}{c^2_w}Z^0_\mu Z^0_\mu H \\ &\quad -\frac{1}{2}ig\Big[W^+_\mu(\phi^0\partial_\mu \phi^- -\phi^- \partial_\mu \phi^0) - W^-_\mu(\phi^0\partial_\mu \phi^+ - \phi^+\partial_\mu \phi^0)\Big]\\ &\quad +\frac{1}{2}g\Big[W^+_\mu(H\partial_\mu \phi^- -\phi^-\partial_\mu H)+ W^-_\mu(H\partial_\mu \phi^+-\phi^+\partial_\mu H)\Big]\\ &\quad + \frac{1}{2}g\frac{1}{c_w}Z^0_\mu(H\partial_\mu \phi^0 -\phi^0 \partial_\mu H) -ig\frac{s^2_w}{c_w}MZ^0_\mu(W^+_\mu\phi^- -W^-_\mu\phi^+) \\ &\quad+ igs_w M A_\mu(W^+_\mu\phi^- - W^-_\mu \phi^+) -ig\frac{1-2c_w^2}{2c_w}Z^0_\mu(\phi^+\partial_\mu \phi^- - \phi^-\partial_\mu \phi^+)\\ &\quad+igs_w A_\mu(\phi^+\partial_\mu \phi^- -\phi^-\partial_\mu \phi^+) -\frac{1}{4}g^2W^+_\mu W^-_\mu \Big[H^2+(\phi^0)^2+2\phi^+\phi^-\Big]\\ &\quad -\frac{1}{8}g^2\frac{1}{c_w^2}Z^0_\mu Z^0_\mu \Big[H^2+(\phi^0)^2+2(2s_w^2-1)^2\phi^+\phi^-\Big]\\ &\quad -\frac{1}{2}g^2\frac{s_w^2}{c_w}Z^0_\mu \phi^0(W^+_\mu\phi^-+W^-_\mu\phi^+) -\frac{1}{2}ig^2\frac{s_w^2}{c_w}Z^0_\mu H(W^+_\mu \phi^- - W^-_\mu\phi^+)\\ &\quad +\frac{1}{2}g^2s_w A_\mu \phi^0(W^+_\mu\phi^-+W^-_\mu\phi^+) +\frac{1}{2}ig^2s_w A_\mu H(W^+_\mu \phi^- - W^-_\mu\phi^+)\\ &\quad - g^2\frac{s_w}{c_w}(2c_w^2-1)Z^0_\mu A_\mu \phi^+\phi^- -g^2s_w^2 A_\mu A_\mu \phi^+\phi^- \\ &\quad + \frac{1}{2}ig_s\lambda^a_{ij}(\bar q_i^\sigma \gamma^\mu q^\sigma_j)g_\mu^a \\\end{align*} \begin{align*} \qquad&\quad -\bar e^\lambda(\gamma\partial+m_e^\lambda)e^\lambda -\bar \nu^\lambda \gamma\partial \nu^\lambda -\bar u_j^\lambda(\gamma\partial+m_u^\lambda)u_j^\lambda -\bar d_j^\lambda(\gamma\partial+m_d^\lambda)d_j^\lambda\\ &\quad+igs_w A_\mu\Big[-(\bar e^\lambda \gamma^\mu e^\lambda) + \frac{2}{3}(\bar u_j^\lambda\gamma^\mu u_j^\lambda) -\frac{1}{3}(\bar d_j^\lambda\gamma^\mu d_j^\lambda)\Big]\\ &\quad+\frac{ig}{4c_w}Z^0_w \Big[\bar \nu^\lambda \gamma^\mu(1+\gamma^5)\nu^\lambda +\bar e^\lambda \gamma^\mu(4s_w^2-1-\gamma^5)e^\lambda \\ &\qquad\qquad\quad + \bar d_j^\lambda\gamma^\mu(\frac{4}{3}s_w^2-1-\gamma^5)d_j^\lambda +\bar u_j^\lambda\gamma^\mu(1-\frac{8}{3}s_w^2+\gamma^5)u_j^\lambda\Big]\\ &\quad +\frac{ig}{2\sqrt 2}W^+_\mu\Big[\bar\nu^\lambda\gamma^\mu(1+\gamma^5)e^\lambda +\bar u_j^\lambda \gamma^\mu(1+\gamma^5)C_{\lambda\kappa}d_j^\kappa\Big]\\ &\quad + \frac{ig}{2\sqrt 2}W^-_\mu\Big[\bar e^\lambda \gamma^\mu(1+\gamma^5)\nu^\lambda +\bar d_j^\kappa C^\dagger_{\kappa\lambda}\gamma^\mu(1+\gamma^5)u_j^\lambda\Big]\\ &\quad +\frac{ig}{2\sqrt 2}\frac{m_e^\lambda}{M}\Big[-\phi^+\bar\nu^\lambda(1-\gamma^5)e^\lambda +\phi^-\bar e^\lambda(1+\gamma^5)\nu^\lambda\Big]\\ &\quad -\frac{g}{2}\frac{m_e^\lambda}{M}\Big[H(\bar e^\lambda e^\lambda)+i\phi^0(\bar e^\lambda\gamma^5 e^\lambda)\Big]\\ &\quad+\frac{ig}{2M\sqrt 2}\phi^+\Big[-m_d^\kappa\bar u_j^\lambda C_{\lambda\kappa}(1-\gamma^5)d_j^\kappa +m_u^\lambda\bar u_j^\lambda C_{\lambda\kappa}(1+\gamma^5)d_j^\kappa\Big]\\ &\quad +\frac{ig}{2M\sqrt 2}\phi^-\Big[m_d^\lambda\bar d_j^\lambda C^\dagger_{\lambda\kappa}(1+\gamma^5)u_j^\kappa -m_u^\kappa\bar d_j^\lambda C^\dagger_{\lambda\kappa}(1-\gamma^5)u_j^\kappa\Big]\\ &\quad -\frac{g}{2}\frac{m_u^\lambda}{M}H(\bar u_j^\lambda u_j^\lambda) -\frac{g}{2}\frac{m_d^\lambda}{M}H(\bar d_j^\lambda d_j^\lambda) \\ &\quad +\frac{ig}{2}\frac{m_u^\lambda}{M}\phi^0(\bar u_j^\lambda\gamma^5 u_j^\lambda) -\frac{ig}{2}\frac{m_d^\lambda}{M}\phi^0(\bar d_j^\lambda\gamma^5 d_j^\lambda)\\ \end{align*} \begin{align*} \qquad&\quad+\bar G^a\partial^2G^a+g_sf^{abc}\partial_\mu \bar G^a G^b g^c_\mu +\bar X^+(\partial^2-M^2)X^++\bar X^-(\partial^2 - M^2)X^-\\ &\quad+\bar X^0(\partial^2-\frac{M^2}{c_w^2})X^0+\bar Y\partial^2 Y \\ &\quad+igc_w W^+_\mu(\partial_\mu \bar X^0 X^- - \partial_\mu \bar X^+X^0)+igs_w W^+_\mu(\partial_\mu\bar YX^--\partial_\mu\bar X^+Y)\\ &\quad+igc_w W^-_\mu(\partial_\mu\bar X^-X^0-\partial_\mu\bar X^0X^+)+igs_w W^-_\mu(\partial_\mu\bar X^-Y-\partial_\mu\bar YX^+)\\ &\quad+igc_w Z^0_\mu(\partial_\mu\bar X^+X^+-\partial_\mu\bar X^-X^-)+igs_w A_\mu (\partial_\mu\bar X^+X^+-\partial_\mu\bar X^-X^-)\\ &\quad-\frac{1}{2}gM(\bar X^+X^+H+\bar X^-X^-H+\frac{1}{c_w^2}\bar X^0X^0H)\\ &\quad+\frac{1-2c_w^2}{2c_w}igM(\bar X^+X^0\phi^+-\bar X^-X^0\phi^-) +\frac{1}{2c_w}igM(\bar X^0X^-\phi^+-\bar X^0X^+\phi^-)\\ &\quad+igMs_w(\bar X^0X^-\phi^+-\bar X^0X^+\phi^-)+\frac{1}{2}igM(\bar X^+X^+\phi^0-\bar X^-X^-\phi^0) \end{align*} 标准模型预言的粒子,如下图 |

|
|
我们不需要写出全部的细节,只需知道上帝如何设计宇宙,标准模型需要三个群 SU(3)_C 、 SU(2)_L 和 U(1)_Y \begin{align*} \mathcal{L}_{SM} = & - \frac{1}{4}G^{a\mu\nu}G^a{}_{\mu\nu} - \frac{1}{4}W^{i\mu\nu}W^i{}_{\mu\nu} - \frac{1}{4}B^{\mu\nu}B_{\mu\nu} \\ & + i\bar{L}D\mkern-10.5mu/ L+i\bar{R}D\mkern-10.5mu/ R +(D_\mu \Phi)^\dagger D^\mu \Phi - V(\Phi) \\ & - \Gamma \bar{L} \Phi R - \Gamma' \bar{L} \tilde{\Phi}R +h.c. \end{align*} 规范场包括(8个胶子 、3个中间玻色子、1个光子) \begin{align*} & G^a{}_{\mu\nu} = \partial_\mu G^a{}_\nu -\partial_\nu G^a{}_\mu + \lambda^a{}_{bc}G^b{}_\mu G^c{}_\nu \\ & W^i{}_{\mu\nu} = \partial_\mu W^i{}_\nu -\partial_\nu W^i{}_\mu +\epsilon^i{}_{jk}W^j{}_\mu W^k{}_\nu \\ & B_{\mu\nu} = \partial_\mu B_\nu - \partial_\nu B_\mu \end{align*} 左手费米子 SU(2)_L 群双重态 \begin{align*} L = \begin{pmatrix} \nu_e \\ e \end{pmatrix}_L , \begin{pmatrix} \nu_\mu \\ \mu \end{pmatrix}_L , \begin{pmatrix} \nu_\tau \\ \tau \end{pmatrix}_L , \begin{pmatrix} u \\ \tilde{d} \end{pmatrix}_L, \begin{pmatrix} c \\ \tilde{s} \end{pmatrix}_L, \begin{pmatrix} t \\ \tilde{b} \end{pmatrix}_L \end{align*} 右手费米子 SU(2) 单态 R = e_R, \mu_R,\tau_R, \nu_{eR},\nu_{\mu R} , \nu_{\tau R} , u_R,d_R,c_R, s_R, t_R,b_R 轻子的协变导数 \begin{align*} & D_\mu \begin{pmatrix} \nu_l \\ l \end{pmatrix}_L = (\partial_\mu - ig \frac{\tau}{2}W_\mu -ig^\prime \frac{Y}{2}B_\mu)\begin{pmatrix} \nu_l \\ l \end{pmatrix}_L \\ & D_\mu l_R = (\partial_\mu -ig^\prime \frac{Y}{2}B_\mu)l_R , \qquad l = e, \mu, \tau \\ & D_\mu \nu_{lR} = \partial_\mu \nu_{lR} \end{align*} 夸克的协变导数 \begin{align*} &D_\mu \begin{pmatrix} u \\ \tilde{d} \end{pmatrix}_L = (\partial_\mu -ig_C \frac{\lambda}{2}G_\mu -ig\frac{\tau}{2}W_\mu -ig^\prime \frac{Y}{2}B_\mu)\begin{pmatrix} u \\ \tilde{d}\end{pmatrix}_L \\ & D_\mu q_R = (\partial_\mu - ig_C\frac{\lambda}{2}G_\mu -ig^\prime \frac{Y}{2}B_\mu)q_R \end{align*} 希格斯玻色子 \begin{align*} \Phi &= \begin{pmatrix} \phi^\dagger \\ \phi^0 \end{pmatrix} , \quad\tilde{\Phi} = i\tau_2\Phi^*,\quad V(\Phi)=-\mu^2\Phi^\dagger\Phi +\lambda(\Phi^\dagger\Phi)^2\\ D_\mu \Phi &= (\partial_\mu - ig\frac{\tau}{2}W_\mu -ig^\prime \frac{Y}{2}B_\mu)\Phi \end{align*} 标准模型稍稍有点复杂的地方是大自然和我们玩了些小把戏,尽管拉格朗日量是对称的,但是真空确是不对称的,这导致了对称性破缺。标准模型的费米子是左右不对称的,如果你观察我们上面写的作用量,会发现 L 和 R 不一样,标准模型的费米子像是一个精神分裂症患者,身体的一半参加弱相互作用,另一部分不参加。标准模型有三代费米子,性质完全一样,但是质量差距很大。最后标准模型漏掉了引力相互作用。所以标准模型并不是物理学家要找的终极理论。 |

|
|
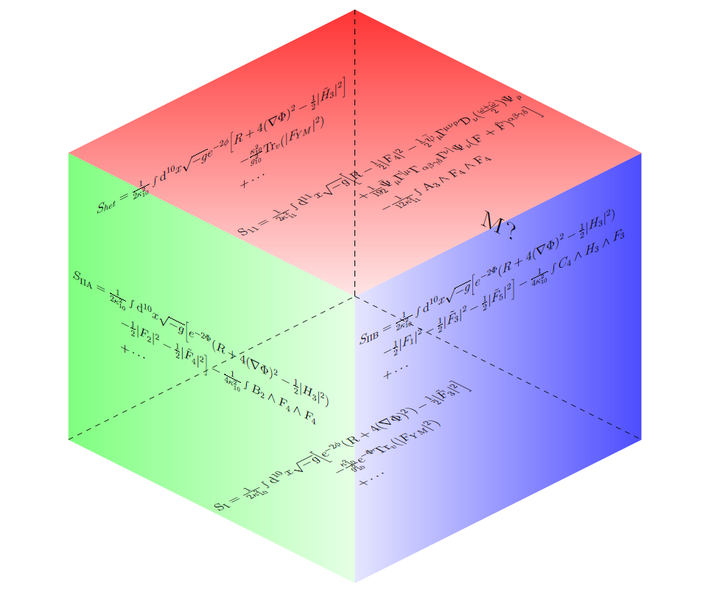
一个有希望的候选者是弦论,弦论的想法很简单,那就是我们的基本粒子都是弦振动产生的。弦只有两种构型: 闭弦 X^\mu (\tau, \sigma) = X^\mu(\tau, \sigma +2\pi) \begin{align*} &X^\mu(\tau, \sigma) = X^\mu{}_L(\tau+\sigma) + X^\mu{}_R(\tau-\sigma) \\ &X^\mu{}_L = \frac{x^\mu}{2} + \frac{p^\mu}{4\pi T}(\tau+\sigma) + \frac{i}{\sqrt{4\pi T}}\sum_{k\ne 0}{\frac{\bar{\alpha}^\mu_k}{k}e^{-ik(\tau+\sigma)}}\\ &X^\mu{}_R = \frac{x^\mu}{2} + \frac{p^\mu}{4\pi T}(\tau-\sigma) + \frac{i}{\sqrt{4\pi T}}\sum_{k\ne 0}{\frac{\alpha^\mu_k}{k}e^{-ik(\tau-\sigma)}} \end{align*} \\ 开弦 X^{\prime \mu} (\tau, \sigma) | _{\sigma =0, \pi}= 0 (Neumann边界条件) \begin{align*} X ^\mu(\tau, \sigma) = x^\mu +\frac{p^\mu \tau}{\pi T} + \frac{i}{\sqrt{\pi T}}\sum_{k \ne 0}{\frac{\alpha^\mu_k}{k}\cos(k\sigma)} \end{align*}\\ 更妙的是在弯曲时空背景下,我们能从弦的量子化过程中重新发现Einstein方程,弦在一般背景下的Polyakov作用量是 \begin{align*} S_p = \frac{1}{4\pi \alpha^\prime} \int_\Sigma \mathrm{d}^2\xi \left [ \sqrt{g}g^{ab}G_{\mu\nu}(X) +\epsilon^{ab}B_{\mu\nu}(X) \right ]\partial_a X^\mu \partial_b X^\nu \\ + \frac{1}{4\pi}\int_\Sigma \mathrm{d}^2\xi \sqrt{g}R^{(2)}\Phi(X) \end{align*} \\ 这个作用量未量子化时有共形不变性 \begin{align*} T^a{}_a =g^{ab}\frac{4\pi\alpha^\prime}{\sqrt{g}} \frac{\delta S_P}{\delta g^{ab}} = 0 \end{align*}\\ 量子化后 }">\mathbf{<} T^a{}_a\mathbf{>} 一般不为0,存在反常。 \begin{align*} T^a{}_a= \frac{\beta_\Phi}{2\pi}\sqrt{g}R^{(2)} + \frac{1}{2\pi}(\beta^G_{\mu\nu}\sqrt{g}g^{ab} +\beta^B_{\mu\nu}\epsilon^{ab})\partial_aX^\mu \partial_bX^\nu \end{align*} \\ 这些 \beta 函数可以通过微扰论来计算, \begin{align*} & \frac{\beta^G_{\mu\nu}}{\alpha^\prime} = R_{\mu\nu} +2\nabla_\mu \nabla_\nu \Phi - \frac{1}{4}H_{\mu\rho\sigma}H_\nu{}^{\rho\sigma} +\mathcal{O}(\alpha^\prime),\\ &\frac{\beta^B_{\mu\nu}}{\alpha^\prime} =-\frac{1}{2}\nabla^\rho H_{\rho\mu\nu} +\nabla^\rho \Phi H_{\rho\mu\nu}+ \mathcal{O}(\alpha^\prime), \\ &\beta^\Phi = \frac{D -26}{6} +\alpha^\prime [ 2(\nabla \Phi)^2 -2 \Box \Phi -\frac{1}{2}R+ \frac{1}{24}H^2] + \mathcal{O}(\alpha^{\prime2}) \end{align*} \\ 其中 H_{\mu\nu\rho} = \partial_\mu B_{\nu\rho} + \partial_\nu B_{\rho\mu} + \partial_\rho B_{\mu\nu} ,D 是时空维度。 当这些 \beta = 0 时,反常消失。我们可以从这些 \beta 函数里发现 Einstein 方程 \begin{align*} \frac{\beta^G_{\mu\nu}}{\alpha^\prime} +G_{\mu\nu}\frac{\beta^\Phi }{\alpha^\prime}=(R_{\mu\nu} - \frac{1}{2}G_{\mu\nu}R) - T^{matter}_{\mu\nu} = 0 \end{align*} \\ 我们也可以从下面的作用量里得出上面的 Einstein 方程 \begin{align*} S = \frac{1}{2\kappa_{26}^2}\int \mathrm{d}^{26}x \sqrt{-G}e^{-2\Phi}\left [R +4(\nabla\Phi)^2 -\frac{1}{12} H^2 + \mathcal{O}(\alpha^\prime) \right ] \end{align*} \\ 世界叶上的共形不变性可以给出背景时空的动力学,弦论可以绕开通常引力量子化中的困难,广义相对论可以认为是弦论的低能有效理论,S 是弦的低能有效作用量。一件有意思的事情是在弦论的情况下,理论的自洽性要求这些 \beta 为0, 更一般的情况下,这些 \beta 函数满足重整化群方程 \begin{align*} \mu \frac{\partial G_{\mu\nu}}{\partial \mu} = \beta^G_{\mu\nu} \end{align*}\\ 它在数学上的版本是 Hamilton 的 Ricci 流方程 \begin{align*} \frac{\partial g_{ij}}{\partial t} = -2R_{ij} \end{align*}\\ 佩雷尔曼在证明庞加莱猜想的首篇论文《The entropy formula for the Ricci flow and its geometric applications》里写到 这是一个极好的例子显示理论物理学和纯数学之间存在着某种神奇的联系,尽管两个理论大相径庭。 玻色弦要求背景时空必须是 26 维,同时还存在超光速粒子。物理学家不是科幻小说家,不喜欢超光速粒子这种玩意儿,因为它会导致真空的不稳定。 解决问题的办法是加入费米子弦、引入超对称。一个局域 N=1 的超弦作用量 \begin{align*} S_P = \frac{1}{4\pi \alpha^\prime} \int_\Sigma \mathrm{d}^2\xi \sqrt{g} \left [ g^{ab}\partial_a X^\mu \partial_b X_\mu + \frac{i}{2} \psi^\mu \partial \mkern-10.5mu/ \psi_\mu + \frac{i}{2}(\chi_a \gamma^b \gamma^a \psi^\mu)(\partial_b X_\mu - \frac{i}{4}\chi_b\psi_\mu) \right ] \end{align*} \\ 在超对称下是不变的 \begin{align*} &\delta g_{ab} = i\epsilon(\gamma_a\chi_b + \gamma_b\chi_a) , \quad\delta\chi_a = 2\nabla_a \epsilon, \\ &\delta X^\mu = i\epsilon\psi^\mu, \quad \delta \psi ^\mu = \gamma^a(\partial_a X^\mu - \frac{i}{2}\chi_a\psi^\mu)\epsilon , \quad\delta \bar{\psi}^\mu = 0 \end{align*} \\ 超弦的模代数 \begin{align*} &[L_m, L_n] = (m -n)L_{m+n} + \frac{c}{12}(m^3-m)\delta_{m+n,0} \\ & \{ G_r,G_s \} = 2L_{r+s}+\frac{c}{12}(4r^2 -1)\delta_{r+s,0} \\ & [L_m , G_r] = \frac{m-2r}{2}G_{m+r} \end{align*} \\ 超共形生成元 \begin{align*} & L_m = \frac{1}{2}\sum_{n\in \mathbf{Z}}{{}^\circ_\circ \alpha^\mu_{m-n}\alpha_{\mu n}{}^\circ_\circ} +\frac{1}{4}\sum_{r\in \mathbf{Z}+\nu}{(2r-m){}^\circ_\circ\psi^\mu_{m-r}\psi_{\mu r}{}^\circ_\circ} +a^m\delta_{m,0}\\ &G_r = \sum_{n \in \mathbf{Z}}{\alpha^\mu_n \psi_{\mu}{}_{r-n}} \end{align*} \\ 让人意外的是物理学家找到不只一种超弦理论,而是找到了5种自洽的超弦理论,对于一个终极理论候选者来说可不是好事情。物理学家发现这五种弦论存在着比对称性更高的关系,那就是对偶性。要了解对偶性,我们要从超弦的低能有效作用量开始。正如我们已经介绍的玻色弦类似,每一种超弦理论都有自己的低能有效理论,这些低能有效理论在超弦理论未发现之前就已经被物理学家发现了,它们就是超引力理论,广义相对论的超对称版本。为了简单我们只写出玻色场部分 \mathrm{IIA} 型 \begin{align*} \mathbf{S}_{\mathrm{IIA}} = \frac{1}{2\kappa^2_{10}}\int \mathrm{d}^{10}x \sqrt{-G}&[ e^{-2\Phi} \Big (R + 4(\nabla\Phi)^2 - \frac{1}{2} |H_3|^2 \Big)\\ & -\frac{1}{2}|F_2|^2-\frac{1}{2} |\widetilde{F}_4|^2] -\frac{1}{4\kappa^2_{10}} \int B_2 \wedge F_4\wedge F_4 \end{align*}\\ \mathrm{IIB} 型 \begin{align*}\mathbf{S}_{\mathrm{IIB}} = \frac{1}{2\kappa^2_{10}}\int \mathrm{d}^{10}x \sqrt{-G}&[ e^{-2\Phi} (R + 4(\nabla\Phi)^2 - \frac{1}{2} |H_3|^2 )-\frac{1}{2}|F_1|^2 \\ &-\frac{1}{2} |\widetilde{F}_3|^2 -\frac{1}{2} |\widetilde {F}_5| ] -\frac{1}{4\kappa^2_{10}} \int C_4 \wedge H_3\wedge F_3\end{align*}\\ \mathrm{I} 型 \begin{align*} \mathbf{S}_{\mathrm{I}} &= \frac{1}{2\kappa^2_{10}}\int \mathrm{d}^{10}x \sqrt{-G}[ e^{-2\Phi}\left (R + 4(\nabla\Phi)^2 \right )\\ & - \frac{1}{2} |\tilde{F}_3|^2-\frac{\kappa^2_{10}}{g^2_{10}}e^{-\Phi}Tr_v(|F_{YM}|^2)] \end{align*} \\ 杂化型两种 SO(32) 和 E_8 \times E_8 \begin{align*} \mathbf{S}_{het} &= \frac{1}{2\kappa^2_{10}}\int \mathrm{d}^{10}x \sqrt{-G}e^{-2\Phi} [ R + 4(\nabla\Phi)^2 \\ &- \frac{1}{2} |\widetilde{H}_3|^2-\frac{\kappa^2_{10}}{g^2_{10}}Tr_v(|F_{YM}|^2) ] \end{align*} \\ 这些超引力理论可以互相转换,它们有一个共同的起源那就是11维超引力 \begin{align*} \mathbf{S}_{11} &= \frac{1}{2\kappa_{11}^2} \int \mathrm{d}^{11}x\sqrt{-G} \{ R - \frac{1}{2} |F_4|^2 - \frac{1}{2}\overline{\Psi}_{\mu}\Gamma^{\mu\nu\rho}\mathcal{D}_{\nu} ( \frac{\omega + \hat{\omega}}{2} )\Psi_\rho \\ &+\frac{1}{192}\overline{\Psi}_\mu\Gamma^{[\mu}\Gamma_{\alpha\beta\gamma\delta}\Gamma^{\nu ]}\Psi_\nu ( F^{\alpha\beta\gamma\delta} + \hat{F}^{\alpha\beta\gamma\delta} ) \}\\ &- \frac{1}{12\kappa_{11}^2}\int A_3 \wedge F_4 \wedge F_4 \end{align*} \\ |
|
|
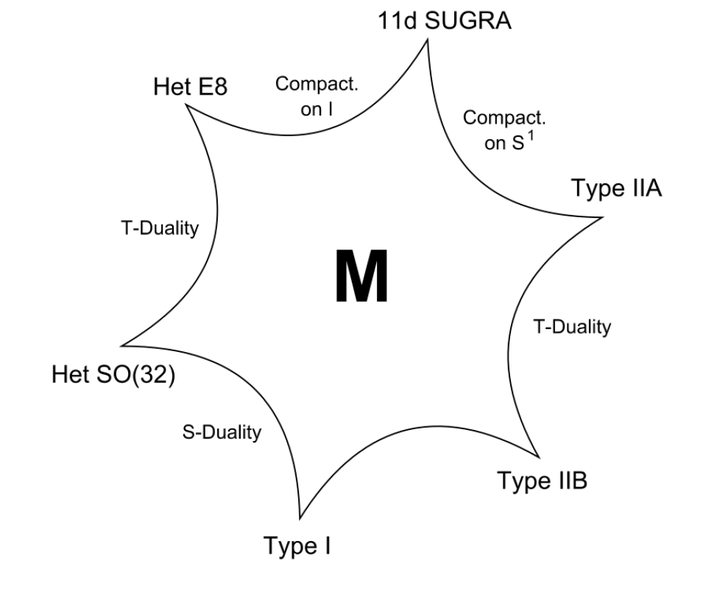
Einstein 的广义相对论和 Maxwell 的电磁场数学上有一个有趣的关系, 如果我们把广义相对论扩展到 5 维即 \begin{align*} S = \int \mathrm{d}^5x\sqrt{-g}R \end{align*}\\ 我们把第5维给卷起来即 x^4 \sim x^4 + 2\pi R ,电磁场 A_\mu 形式上就产生了。5维的时空线元 \begin{align*} \mathrm{d}s^2 = g^{(5)}_{MN}\mathrm{d}x^M\mathrm{d}x^N = g^{(4)}_{\mu\nu}\mathrm{d}x^\mu \mathrm{d}x^\nu + g^{(4)}_{44}(\mathrm{d}x^4 + A_\mu \mathrm{d}x^\mu)^2 \end{align*}\\ 我们把 g^{(4)}_{44} 写作 e^{2\phi} . 5维的 Ricci 标量曲率可以分解为 \begin{align*} R^{(5)} = R^{(4)} - 2e^{-\phi}\nabla^2e^\phi - \frac{1}{4}e^{2\phi}F_{\mu\nu}F^{\mu\nu} \end{align*}\\ 其中 \begin{align*} F_{\mu\nu} = \partial_\mu A_\nu -\partial_\nu A_\mu \end{align*}\\ 和 \begin{align*} g^{(4)}_{\mu\nu} = g^{(5)}_{\mu\nu} - e^{-2\phi}A_\mu A_\nu \end{align*}\\ 我们就可以得到 \begin{align*} S &= \frac{1}{16\pi G_5} \int_{M^4 \times S^1} \mathrm{d}^5x\sqrt{-g^{(5)}}R^{(5)}\\ & =\frac{1}{16\pi G_4} \int_{M^4}\mathrm{d}^4x \sqrt{-g^{(4)}}\left (R^{(4)} - \frac{3}{2}\partial_\mu \phi \partial^\mu \phi -\frac{1}{4}e^{3\phi}F_{\mu\nu}F^{\mu\nu}\right ) \end{align*} \\ 牛顿引力常数有 \frac{2\pi R}{G_5} = \frac{1}{G_4} 。这种把某个时空维度卷起来的方法最早是卡鲁查和克莱因发现。 11 维超引力和 \mathrm{IIA} 超引力也可以这样玩,我们可以把第十一个维度卷起来 x^{10}\sim x^{10} +2\pi R 类似的 \begin{align*} G^{11}_{MN} \mathrm{d}x^M\mathrm{d}x^N = e^{-\frac{2}{3}\Phi}G^{10}_{\mu\nu}\mathrm{d}x^\mu \mathrm{d}x^\nu +e^{\frac{4}{3}\Phi}\left (dx^{10} + A_\mu \mathrm{d} x^\mu \right )^2 \end{align*}\\ 这里不展示详细的过程。我们上面说过10维时空的每一种超弦理论都有相对应的超引力理论作为其低能有效理论,反过来说11维超引力理论也是某个理论的低能有效理论,但是自洽的弦论只能出现在10维或26维,所以这个理论不可能是弦论,这个未知的理论叫做M理论,我们目前只能通过11维超引力理论来理解它的一些性质。M理论和10维的超弦理论组成了一张对偶关系网 |
|
|
看起来M理论就是物理学家心中的那个可以写在纸上的终极理论,M理论有很多有意思的东西,比如D-branes、AdS /CFT 、黑洞熵的统计力学解释、弦宇宙学等等,暂时写到这里 。。。 |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |