天天财汇 购物 网址 万年历 小说 | 三峰软件 小游戏 视频
TxT小说阅读器
↓小说语音阅读,小说下载↓ 		一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓ 		图片批量下载器
↓批量下载图片,美女图库↓ 		图片自动播放器
↓图片自动播放,产品展示↓
首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行]
股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事
商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏--
  天天财汇 -> 自然科学 -> 如何看待 DeepMind 新发布的 AlphaGeometry? -> 正文阅读

[自然科学]如何看待 DeepMind 新发布的 AlphaGeometry?

[收藏本文] 【下载本文】
Deepmind 声称在几何问题求解方面接近国际数学奥林匹克竞赛(IMO)金牌水平. Deepmind blog: AlphaGeometry: An…
先贴一下我在隔壁的自问自答，极简总结了一下论文的主要想法，以及二作吴宇怀对文章的的精彩总结。
这里主要谈谈它到底多大程度上拓展了LLM范式的能力，跟所谓“AGI”有什么关系，它是否值得一场狂欢。
首先它代表了一类“LLM+足够好的数据等价于足够好的智能”的观点。但是正像Lecun等人常提到的，LLM对数据的利用效率实在堪忧，它在一亿量级的数据上训练，其中对任务起到关键作用的带辅助线数据达到了900w个，显然这和人类的训练方式有很大不同。一种可能的辩护是，人类认知能力的先验要比随机初始化的LLM强很多，尽管我们并不知道它们，那么如果更大的数据量能够让从零起步的网络自行学到这些先验，我们不妨以此范式作为通向更高智能的标准解决方案。但是alphageometry似乎也让我们看到，此范式甚至并不是一种“在无限资源下”“数学上理想的”可行解，因为几何问题空间的分布比较狭窄，而通用数学任务的构造非常丰富。
以一般的定理证明任务为例，Lean Mathlib目前有5w+条已被形式化的定理，这些定理分布广泛，充分涵盖了数学的各个领域，每一个定理的证明构造方式都几乎是“单例的”，或者用LLM术语叫few-shot，如果用alphageometry的范式估算大概需要5w*900w的数据量级才能实现mathlib所涵盖的比较初等的数学问题的自动证明。我们可能需要反思人类是如何在单例上实现数学学习的，例如前段时间火的神秘的q-star，需要强化学习和LLM的某种融合。
但是另一方面，在LLM范式内部，经过symbolic system生成verified data会显著提高LLM性能，已经是OpenAI以及Google的共识。数学恰好就是容易verify的领域，大胆预言数学+LLM会成为下一阶段的学术热点。
至于所谓AGI，我当下依旧认为我们讨论它还为时尚早。LLM是强大的模式捕捉器不假，它可以在许多任务上给logic engine提供接近“人类直觉”的指导，很符合system1和system2的框架。但是人类似乎还具备许多更深刻的能力，例如几何直观，更强的组合泛化能力，封装概念的能力等等。
总之我还是很敬佩一作trieu能用整个博士生涯肝出一篇Nature这样强大的动手能力和毅力的，诚如yuhuai所说，整个工作思路很直接但是细节非常的不平凡，我对这么solid且sound的工作只能叹服了。
本回答包含了作者自己的看法的介绍，本人对于AlphaGeometry的看法与本人实际运行的测试。欢迎读者阅读。论文的介绍，可见其他回答，如 如何看待1.17Nature论文《无需人类示例即可解决奥赛几何问题》发布AlphaGeometry？
作者自己对于alphageometry方法学的评价
按照论文，简单说下alphageometry的想法，按照作者在文章方法部分的总结，alphageometry的想法可以概括如下，而且作者也探讨了，这套框架移植到其他领域，如组合问题的可能性：
Our paper shows that language models can learn to come up with auxiliary constructions from synthetic data, in which problem statements and auxiliary constructions are randomly generated together and then separated using the traceback algorithm to identify the dependency difference. Concretely, the AlphaGeometry framework requires the following ingredients:
(1) An implementation of the domain’s objects and definitions.
(2) A random premise sampler.
(3) The symbolic engine(s) that operate within the implementation (1).
(4) A traceback procedure for the symbolic engine.
Using these four ingredients and the algorithm described in the main text, one can generate synthetic data for any target domain. As shown in our paper, there are non-trivial engineering challenges in building each ingredient. For example, current formalizations of combinatorics are very nascent, posing challenges to (1) and (2). Also, building powerful symbolic engines for different domains requires deep domainexpertise, posing challenges to (3) and (4). We consider applying this framework to a wider scope as future work and look forward to further innovations that tackle these challenges.
翻译为：
我们的研究表明，语言模型可以学习从合成数据中构造辅助线，其中问题陈述和辅助线是一起随机生成的，然后使用回溯算法分离出来，以识别依赖差异。具体来说，AlphaGeometry框架需要以下要素:
(1)对一个领域的对象和定义的实现 （译者注，这个可以见作者的def.txt文件）。
(2)随机前提采样器（译者注，这个作者没有提供相关代码，相关细节也写的不是那么详细，但这也是一个非常关键的步骤）。
(3)在实现(1)中运行的符号引擎（译者注，作者的DD+AR引擎，非常牛逼）。
(4)符号引擎的追踪过程（译者注，新版代码是可以画图的）。
使用这四种成分和正文中描述的算法，可以为任何目标领域生成合成数据。正如我们的论文所示，在构建每个成分时都存在重大的工程挑战。例如，目前组合数学的形式化还处于初期，对(1)和(2)提出了挑战。此外，为不同领域构建强大的符号引擎需要深入的领域专业知识，对(3)和(4)提出了挑战。我们考虑将该框架应用于更广泛的范围，作为未来的工作，并期待进一步的创新来应对这些挑战。
期待作者未来的工作吧。
看法
利用机器证明数学定理的想法可以追踪到莱布尼茨，可行的方案则是从布尔和康托尔，罗素开始，在二战后随着计算机和人工智能的兴起逐渐成为一个很活跃的领域，在其中的子领域，平面几何题证明方面，我国的著名学者吴文俊院士做出过非常牛逼的贡献，世人称为吴方法。这也是AlphaGeometry论文中用来比较的一个方法之一。近年来，在利用大语言模型证明数学问题方面，国人也和老前辈一样没有落后时代，例如好未来开发的MathGPT（评论区说好未来的这个有争议）


AI4math与AI4Science之间的最大区别在于，AI4math在理解问题、开发和验证过程中的非人力成本相对较低。因此，利用AI4math来研究AI的推理能力，既适合大型公司，也适合小型团队。这一赛道具有广泛的应用前景和巨大的潜力，值得投入更多的资源和精力进行深入探索。
此外，其他回答提到了作者使用的合成数据。我觉得非常牛逼的一点是，作者使用了大量的算力的来生成合成数据，而且庞大的合成数据中，并没有包含IMO的数据（自然也没有大模型一直被诟病的数据污染问题），
After running this process on 100,000 CPU workers for 72 h, we obtained roughly 500 million synthetic proof examples. We reformat the proof statements to their canonical form (for example, sorting arguments of individual terms and sorting terms within the same proof step, etc.) to avoid shallow deduplication against itself and against the test set. At the end, we obtain 100 million unique theorem–proof examples. A total of 9 million examples involves at least one auxiliary construction. We find no IMO-AG-30 problems in the synthetic data. On the set of geometry problems collected in JGEX, which consists mainly of problems with moderate difficulty and well-known theorems, we find nearly 20 problems in the synthetic data.This suggests that the training data covered a fair amount of common knowledge in geometry, but the space of more sophisticated theorems is still much larger.
这提示了平面几何难题的空间还是很大的，可能人力穷极一生，也很难把这么多难题做完。而且，alphageometry会有所谓玄乎的涌现能力吗，我个人略持怀疑态度。因为有些漂亮的证明，像alphageometry似乎是很难生成的。


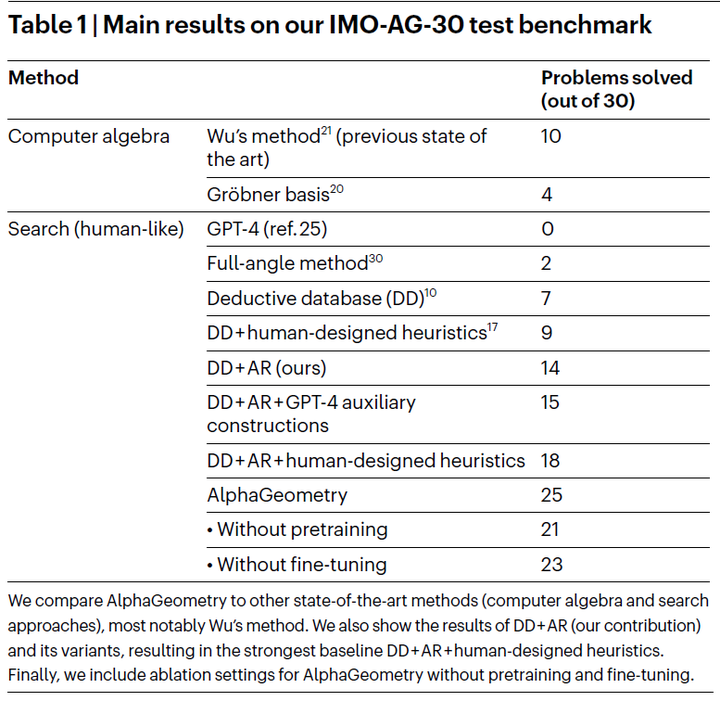
所以IMO，CMO高联这样的比赛还是可以暂时一直比下去，暂时不会像围棋一样。
初步测试
----2024.01.20 更新----
这一部分初步测试部分，使用了简单的参数，不怎么占计算资源。但是如果要达到作者的效果，如下图，需要调整参数，作者在github上的代码是阉割过的，没有并行的功能，所以实际上可能还得在工程上做些调整。
我们用默认参数，Beam size =2 ,serach depth = 2, batch_size = 2只解决了13道imo题目。再更一步的测试中，我们Beam size =4 ,serach depth = 4, batch_size = 4，可以解决15道IMO题目


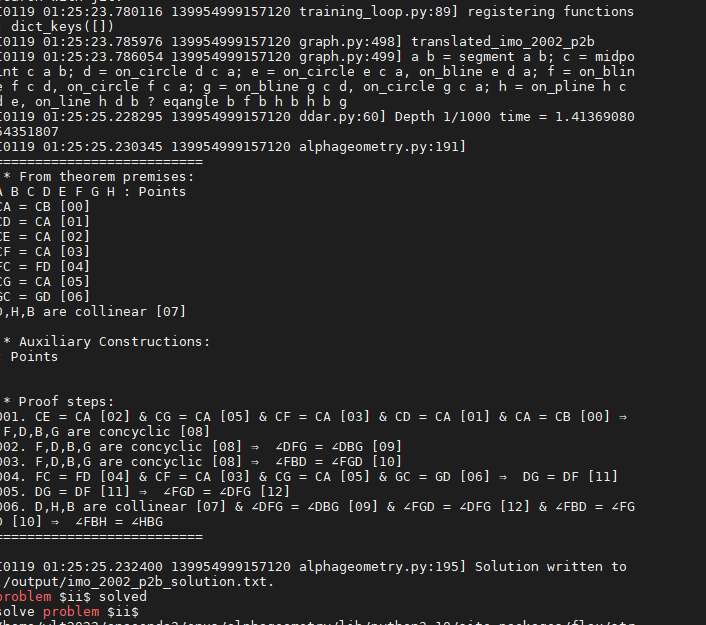
输入
作者团队提供了alphafold的使用代码https://github.com/google-deepmind/alphageometry，我们按照官网教程安装了alphageometry所需要包，对其进行了测试
总的来说，作者提供的代码是已经训练好的模型，可以直接根据将转换成文本的几何问题生成证明。而且不是特别占用计算资源，可能就和利用训练好的lora模型生成图片一样。
我们对于作者提供的30个IMO几何题进行遍历；几何题在文件imo_ag_30.txt中，我们选择前几个给大家看一眼：

translated_imo_2000_p1
a b = segment a b; g1 = on_tline g1 a a b; g2 = on_tline g2 b b a; m = on_circle m g1 a, on_circle m g2 b; n = on_circle n g1 a, on_circle n g2 b; c = on_pline c m a b, on_circle c g1 a; d = on_pline d m a b, on_circle d g2 b; e = on_line e a c, on_line e b d; p = on_line p a n, on_line p c d; q = on_line q b n, on_line q c d ? cong e p e q
translated_imo_2000_p6
a b c = triangle a b c; h = orthocenter h a b c; t1 t2 t3 i = incenter2 t1 t2 t3 i a b c; h1 = foot h1 a b c; h2 = foot h2 b c a; h3 = foot h3 c a b; x1 = reflect x1 h1 t1 t2; x2 = reflect x2 h2 t1 t2; y2 = reflect y2 h2 t2 t3; y3 = reflect y3 h3 t2 t3; z = on_line z x1 x2, on_line z y2 y3 ? cong i z i t1
translated_imo_2002_p2a
b c = segment b c; o = midpoint o b c; a = on_circle a o b; d = on_circle d o b, on_bline d a b; e = on_bline e o a, on_circle e o b; f = on_bline f o a, on_circle f o b; j = on_pline j o a d, on_line j a c ? eqangle e c e j e j e f
translated_imo_2002_p2b
b c = segment b c; o = midpoint o b c; a = on_circle a o b; d = on_circle d o b, on_bline d a b; e = on_bline e o a, on_circle e o b; f = on_bline f o a, on_circle f o b; j = on_pline j o a d, on_line j a c ? eqangle c e c j c j c f

代码
我们遍历的代码如下：

#!/bin/bash
DATA=ag_ckpt_vocab

MELIAD_PATH=meliad_lib/meliad
#mkdir -p $MELIAD_PATH
#git clone https://github.com/google-research/meliad $MELIAD_PATH
export PYTHONPATH=$PYTHONPATH:$MELIAD_PATH

DDAR_ARGS=(
  --defs_file=$(pwd)/defs.txt \
  --rules_file=$(pwd)/rules.txt \
);

BATCH_SIZE=2
BEAM_SIZE=2
DEPTH=2

SEARCH_ARGS=(
  --beam_size=$BEAM_SIZE
  --search_depth=$DEPTH
)

LM_ARGS=(
  --ckpt_path=$DATA \
  --vocab_path=$DATA/geometry.757.model \
  --gin_search_paths=$MELIAD_PATH/transformer/configs \
  --gin_file=base_htrans.gin \
  --gin_file=size/medium_150M.gin \
  --gin_file=options/positions_t5.gin \
  --gin_file=options/lr_cosine_decay.gin \
  --gin_file=options/seq_1024_nocache.gin \
  --gin_file=geometry_150M_generate.gin \
  --gin_param=DecoderOnlyLanguageModelGenerate.output_token_losses=True \
  --gin_param=TransformerTaskConfig.batch_size=$BATCH_SIZE \
  --gin_param=TransformerTaskConfig.sequence_length=128 \
  --gin_param=Trainer.restore_state_variables=False
);

echo $PYTHONPATH

#INPUT_FILE=examples.txt
INPUT_FILE=imo_ag_30.txt

for ii in $(cat $INPUT_FILE | grep "translated"); 
do
    echo 'solve problem $ii$'
    python -m alphageometry \
        --alsologtostderr \
        --problems_file=$(pwd)/$INPUT_FILE \
        --problem_name=${ii} \
        --mode=alphageometry \
        --out_file=./output/${ii#"translated_"}_solution.txt \
        "${DDAR_ARGS[@]}" \
        "${SEARCH_ARGS[@]}" \
        "${LM_ARGS[@]}"
    echo 'problem $ii$ solved'
done

输出
然后中间的运行结果如下：


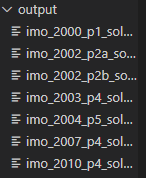
我们可以在output文件夹中看到相应问题的alphafold给出的证明：


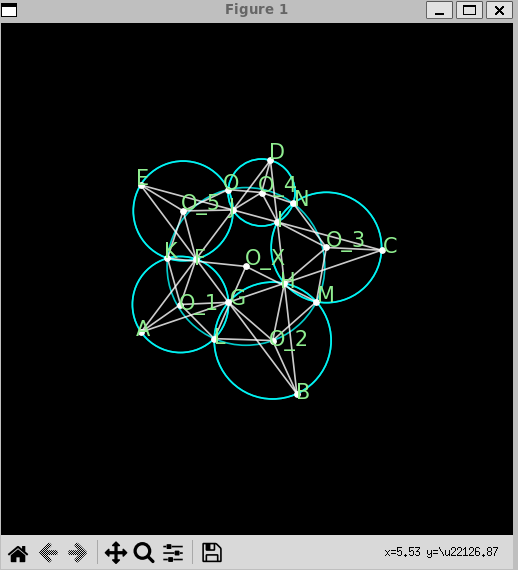
我们选择imo_2007_p4_solution.txt文件打开，这是问题imo_2007_p4的alphageometry给出的解：

==========================
 * From theorem premises:
A B C D E F G H I J K : Points
DB = DC [00]
DA = DB [01]
DE = DA [02]
EA = EB [03]
C,F,A are collinear [04]
FC = FA [05]
C,G,B are collinear [06]
GC = GB [07]
G,D,H are collinear [08]
C,H,E are collinear [09]
F,D,I are collinear [10]
C,E,I are collinear [11]
C,E,J are collinear [12]
FJ ? CE [13]
C,E,K are collinear [14]
CE ? KG [15]

 * Auxiliary Constructions:
: Points


 * Proof steps:
001. DB = DC [00] & GC = GB [07] ?  BC ? DG [16]
002. DA = DB [01] & DB = DC [00] ?  DC = DA [17]
003. DC = DA [17] & FC = FA [05] ?  AC ? DF [18]
004. C,F,A are collinear [04] & F,D,I are collinear [10] & G,D,H are collinear [08] & C,G,B are collinear [06] & BC ? DG [16] & AC ? DF [18] ?  ∠CFI = ∠HGC [19]
005. DB = DC [00] & DA = DB [01] & DE = DA [02] ?  D is the circumcenter of \Delta ECB [20]
006. DB = DC [00] & DA = DB [01] & DE = DA [02] ?  D is the circumcenter of \Delta ECA [21]
007. DB = DC [00] & DA = DB [01] & DE = DA [02] ?  DE = DC [22]
008. C,G,B are collinear [06] & GC = GB [07] ?  G is midpoint of CB [23]
009. D is the circumcenter of \Delta ECB [20] & G is midpoint of CB [23] ?  ∠DBE = ∠(DG-CE) [24]
010. DA = DB [01] & EA = EB [03] (SSS)?  ∠EAD = ∠DBE [25]
011. C,F,A are collinear [04] & FC = FA [05] ?  F is midpoint of CA [26]
012. D is the circumcenter of \Delta ECA [21] & F is midpoint of CA [26] ?  ∠EAD = ∠(CE-DF) [27]
013. C,E,I are collinear [11] & F,D,I are collinear [10] & G,H,D are collinear [08] & C,H,E are collinear [09] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠CIF = ∠GHC [28]
014. ∠CFI = ∠HGC [19] & ∠CIF = ∠GHC [28] (Similar Triangles)?  IC:HC = IF:HG [29]
015. F,D,I are collinear [10] & DF ? AC [18] ?  IF ? CA [30]
016. F is midpoint of CA [26] & IF ? CA [30] ?  IC = IA [31]
017. G,H,D are collinear [08] & DG ? BC [16] ?  HG ? CB [32]
018. G is midpoint of CB [23] & HG ? CB [32] ?  HC = HB [33]
019. C,E,J are collinear [12] & C,E,I are collinear [11] & C,E,K are collinear [14] & C,H,E are collinear [09] & FJ ? CE [13] & CE ? KG [15] ?  ∠FJI = ∠HKG [34]
020. F,D,I are collinear [10] & C,E,J are collinear [12] & C,E,I are collinear [11] & C,E,K are collinear [14] & C,H,E are collinear [09] & G,H,D are collinear [08] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠FIJ = ∠KHG [35]
021. ∠FJI = ∠HKG [34] & ∠FIJ = ∠KHG [35] (Similar Triangles)?  GK:FJ = GH:FI [36]
022. DE = DC [22] ?  ∠DEC = ∠ECD [37]
023. C,E,I are collinear [11] & C,H,E are collinear [09] & ∠DEC = ∠ECD [37] ?  ∠DEI = ∠HCD [38]
024. F,D,I are collinear [10] & C,E,I are collinear [11] & C,H,E are collinear [09] & G,H,D are collinear [08] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠DIE = ∠CHD [39]
025. ∠DEI = ∠HCD [38] & ∠DIE = ∠CHD [39] (Similar Triangles)?  ED:CD = EI:CH [40]
026. C,H,E are collinear [09] & C,E,I are collinear [11] & ∠DEC = ∠ECD [37] ?  ∠DEH = ∠ICD [41]
027. G,H,D are collinear [08] & C,H,E are collinear [09] & C,E,I are collinear [11] & F,D,I are collinear [10] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠DHE = ∠CID [42]
028. ∠DEH = ∠ICD [41] & ∠DHE = ∠CID [42] (Similar Triangles)?  ED:CD = EH:CI [43]
029. IC:HC = IF:HG [29] & IC = IA [31] & HC = HB [33] & GK:FJ = GH:FI [36] & ED:CD = EI:CH [40] & DE = DC [22] & ED:CD = EH:CI [43] ?  GK:FJ = EI:EH
==========================

输出的图
----2024.01.22 更新-----
通过对作者代码的仔细研读，我发现了一种快速根据题设生成题图的方法。已经提交了alphageometry下面的issue，这里分享给大家
前提是下载好代码以及安装好依赖包，然后运行如下的python代码，最后会调用matplotlib里的串口来画图，不过请注意，由于点的坐标随机生成，所以画图的时候要多试几次，已得到美观的结果，如果需要发表级别的图，还是建议用latex里的tkz-eculid手绘。

import unittest
from absl.testing import absltest
import dd
import graph as gh
import problem as pr

txt = 'f g h i j = pentagon f g h i j; a = intersection_ll a f j g h; b = intersection_ll b f g h i; c = intersection_ll c g h i j; d = intersection_ll d h i f j; e = intersection_ll e f g i j; o1 = circle o1 a f g; o2 = circle o2 b g h; o3 = circle o3 c h i; o4 = circle o4 d j i; o5 = circle o5 e j f; k = intersection_cc k o5 o1 f; l = intersection_cc l o1 o2 g; m = intersection_cc m o2 o3 h; n = intersection_cc n o3 o4 i; o = intersection_cc o o4 o5 j; ox = circle k l m ? cyclic k l m n'
defs = pr.Definition.from_txt_file('defs.txt', to_dict=True)
p = pr.Problem.from_txt(txt,translate=False)
g, _ = gh.Graph.build_problem(p, defs)
goal_args = g.names2nodes(p.goal.args)
gh.nm.draw(
      g.type2nodes[gh.Point],
      g.type2nodes[gh.Line],
      g.type2nodes[gh.Circle],
      g.type2nodes[gh.Segment])



----
在最新版的alphageometry中，作者提供了Display the graphical model的功能，该功能应该是通过调用matplotlib的画图设备实现的，注意到，作者在构造的过程，用的类似于尺柜作图的方式，因此，一些不必要的圆没有隐藏，而且还没有做到展示上的美观，不容易理解。因此，我们后期，还是用latex的tkz-euclid来做结果的可视化。


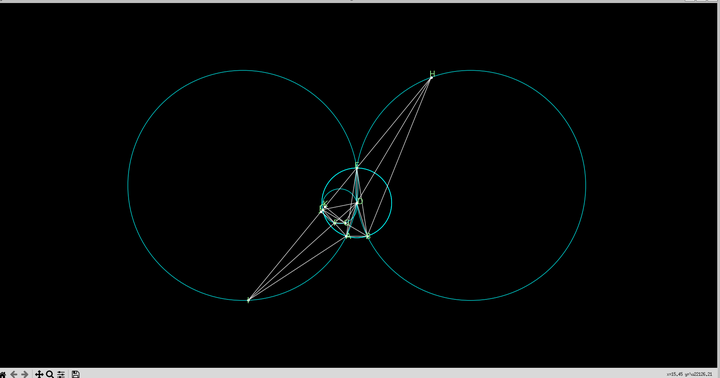
生成的图


放大版确认与核对
上面29步的证明，到底对不对呢？我们进行了检查。
首先，我们明确题目和对应的图：
根据IMO官网，2007P4原题为：
Problem 4. In triangle ABC the bisector of angle BCA intersects the circumcircle again at R, the perpendicular bisector of BC at P, and the perpendicular bisector of AC at Q. The midpoint of BC is K and the midpoint of AC is L. Prove that the triangles RPK and RQL have the same area.
作者对原输入做了调整：
translated_imo_2007_p4
a b c = triangle a b c; o = circle o a b c; r = on_circle r o a, on_bline r a b; l = midpoint l c a; k = midpoint k c b; p = on_line p o k, on_line p c r; q = on_line q o l, on_line q c r; l1 = foot l1 l c r; k1 = foot k1 k c r ? eqratio k k1 l l1 r q r p
而实际上，运行后alphageometry求解的问题为
a b c = triangle a b c; d = circle d a b c; e = on_circle e d a, on_bline e a b; f = midpoint f c a; g = midpoint g c b; h = on_line h d g, on_line h c e; i = on_line i d f, on_line i c e; j = foot j f c e; k = foot k g c e ? eqratio g k f j e i e h
这段机器码，换成中文就是：
已知,三角形ABC的外切圆的圆心为D（记为圆（D,A））。E是圆上一点，且E在AB的中垂线上。F，G分别是边AC，边BC的中点。FD交CE于I,DG交CE于H。FJ ? CE于J，KG ? CE与K。求证： GK:FJ = EI:EH
对应的图为：


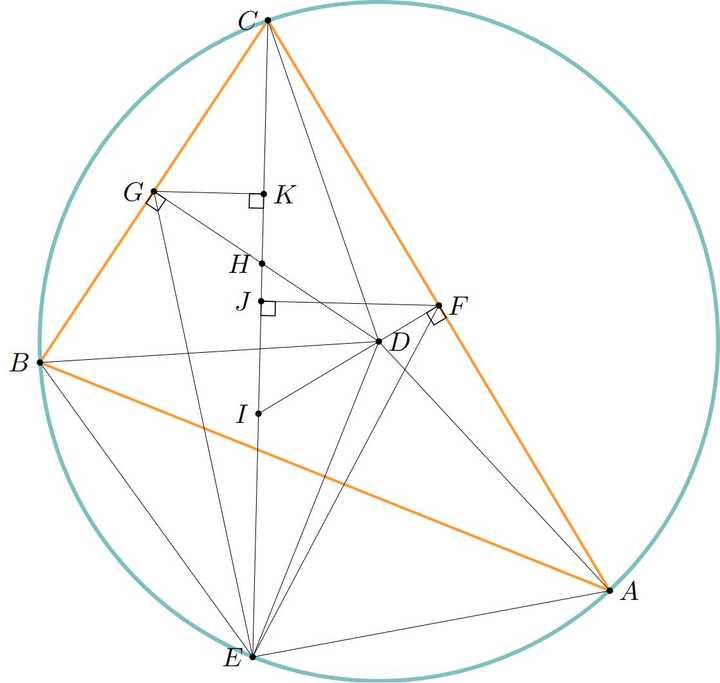
imo_2007_p4
我们现在来看机器生成的证明，我对一些步骤做了注释，确认是没有问题的

001. DB = DC [00] & GC = GB [07] ?  BC ? DG [16]
002. DA = DB [01] & DB = DC [00] ?  DC = DA [17]
003. DC = DA [17] & FC = FA [05] ?  AC ? DF [18]
004. C,F,A 共线 [04] & F,D,I 共线 [10] & G,D,H 共线 [08] & C,G,B 共线 [06] & BC ? DG [16] & AC ? DF [18] ?  ∠CFI = ∠HGC [19]
005. DB = DC [00] & DA = DB [01] & DE = DA [02] ?  D 是外接圆弧ECB对应的圆心 [20]
006. DB = DC [00] & DA = DB [01] & DE = DA [02] ?  D 是外接圆弧ECA对应的圆心 [21]
007. DB = DC [00] & DA = DB [01] & DE = DA [02] ?  DE = DC [22]
以上几步，在实际书写的时候是可以忽略的。

008. C,G,B 共线 [06] & GC = GB [07] ?  G是CB的中点 [23]
009. D 是外接圆弧ECB对应的圆心 [20] & G是CB的中点 [23] ?  ∠DBE = ∠(DG,CE) [24]
其中∠(DG,CE) 为方向角，即直线DG顺时针旋转到CE所需要的角度；
在alphageometyr的推理规则（rules.txt)文件里有，这么一条:
circle O A B C, midp M B C => eqangle A B A C O B O M
注意到，这就是圆周角定理
因此有∠DBE=∠DBA+∠EBA=90-∠BDE+∠ECA=90-2∠BCE+∠ECA=90-2∠BCE+∠BCE=90-∠BCE=  ∠(DG,CE) 

010. DA = DB [01] & EA = EB [03] (SSS)?  ∠EAD = ∠DBE [25]
011. C,F,A 共线 [04] & FC = FA [05] ?  F是CA的中点 [26]
012. D 是外接圆弧ECA对应的圆心 [21] & F是CA的中点 [26] ?  ∠EAD = ∠(CE-DF) [27]
同009。
∠EAD = ∠BAE + ∠BAD = ∠BCE + 90 - ∠ADE = ∠ACE + 90 - 2∠ACE = 90 - ∠ACE = ∠(CE-DF) 


013. C,E,I 共线 [11] & F,D,I 共线 [10] & G,H,D 共线 [08] & C,H,E 共线 [09] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠CIF = ∠GHC [28]
014. ∠CFI = ∠HGC [19] & ∠CIF = ∠GHC [28] (Similar Triangles)?  IC:HC = IF:HG [29]
015. F,D,I 共线 [10] & DF ? AC [18] ?  IF ? CA [30]
016. F是CA的中点 [26] & IF ? CA [30] ?  IC = IA [31]
017. G,H,D 共线 [08] & DG ? BC [16] ?  HG ? CB [32]
018. G是CB的中点 [23] & HG ? CB [32] ?  HC = HB [33]
019. C,E,J 共线 [12] & C,E,I 共线 [11] & C,E,K 共线 [14] & C,H,E 共线 [09] & FJ ? CE [13] & CE ? KG [15] ?  ∠FJI = ∠HKG [34]
020. F,D,I 共线 [10] & C,E,J 共线 [12] & C,E,I 共线 [11] & C,E,K 共线 [14] & C,H,E 共线 [09] & G,H,D 共线 [08] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠FIJ = ∠KHG [35]
021. ∠FJI = ∠HKG [34] & ∠FIJ = ∠KHG [35] (Similar Triangles)?  GK:FJ = GH:FI [36]

如果是人来写，这步不会这么繁琐。

022. DE = DC [22] ?  ∠DEC = ∠ECD [37]
023. C,E,I 共线 [11] & C,H,E 共线 [09] & ∠DEC = ∠ECD [37] ?  ∠DEI = ∠HCD [38]
024. F,D,I 共线 [10] & C,E,I 共线 [11] & C,H,E 共线 [09] & G,H,D 共线 [08] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠DIE = ∠CHD [39]
025. ∠DEI = ∠HCD [38] & ∠DIE = ∠CHD [39] (Similar Triangles)?  ED:CD = EI:CH [40]
026. C,H,E 共线 [09] & C,E,I 共线 [11] & ∠DEC = ∠ECD [37] ?  ∠DEH = ∠ICD [41]
027. G,H,D 共线 [08] & C,H,E 共线 [09] & C,E,I 共线 [11] & F,D,I 共线 [10] & ∠DBE = ∠(DG-CE) [24] & ∠EAD = ∠DBE [25] & ∠EAD = ∠(CE-DF) [27] ?  ∠DHE = ∠CID [42]
028. ∠DEH = ∠ICD [41] & ∠DHE = ∠CID [42] (Similar Triangles)?  ED:CD = EH:CI [43]
029. IC:HC = IF:HG [29] & IC = IA [31] & HC = HB [33] & GK:FJ = GH:FI [36] & ED:CD = EI:CH [40] & DE = DC [22] & ED:CD = EH:CI [43] ?  GK:FJ = EI:EH

这步因为 
ED:CD = EI:CH [40] & DE = DC [22] & ED:CD = EH:CI [43] 
	? HC=EI & IC = EH
IC:HC = IF:HG [29] & IC = IA [31] & HC = HB [33] & GK:FJ = GH:FI [36]
	? GK:FJ = HC:IC
	? GK:FJ = EI:EH

作者补充材料给出的结果
值得注意的事情是：
对照作者提供的补充材料，我们发现这个结果与补充的材料给出的结果的符号不太一样，这是因为alphageometry调整了点的符号。显然补充材料里，作者还是人为的对机器生成的证明做了整理。






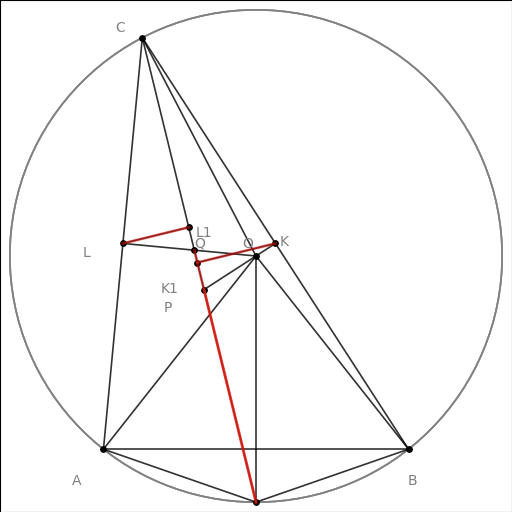
原论文的补充材料更进一步的测试说明
我们以参数BATCH_SIZE=4，BEAM_SIZE=4，DEPTH=4可以将表现提升到解决15道题


alphageometry给出的解
其中，imo_2000_p6，imo_2015_p3都是非常难的题（可见下面，alphageometry原论文的表），在这个参数下，alphageometry都能给出证明。我们这个参数下，对于2019_p6的求解失败了，可能提升参数与优化代码，情况会有改善。


IMO 2000 P6
我们简单的展示这两个问题，以及我们用alphageometry跑出来的证明


来自补充材料



alphageometry生成的证明：
==========================
 * From theorem premises:
A B C H E F G I J K L M N O P : Points
∠HCA = ∠BCH [00]
∠BAH = ∠HAC [01]
B,C,E are collinear [02]
BC ? HE [03]
F,C,A are collinear [04]
CA ? HF [05]
G,B,A are collinear [06]
GH ? AB [07]
BC ? IA [08]
B,C,I are collinear [09]
J,C,A are collinear [10]
CA ? JB [11]
B,A,K are collinear [12]
AB ? KC [13]
EI = EL [14]
FI = FL [15]
FJ = FM [16]
EJ = EM [17]
FJ = FN [18]
GJ = GN [19]
FK = FO [20]
GK = GO [21]
P,N,O are collinear [22]
P,M,L are collinear [23]

 * Auxiliary Constructions:
D Q R S : Points
AD ? BC [24]
BD ? AC [25]
H,B,Q are collinear [26]
QH = QB [27]
H,R,A are collinear [28]
RH = RA [29]
B,S,A are collinear [30]
SB = SA [31]

 * Proof steps:
001. F,C,A are collinear [04] & B,C,E are collinear [02] & AD ? BC [24] & BD ? AC [25] & CA ? HF [05] & BC ? HE [03] ?  ∠HFC = ∠CEH [32]
002. F,C,A are collinear [04] & B,C,E are collinear [02] & ∠HCA = ∠BCH [00] ?  ∠HCF = ∠ECH [33]
003. ∠HFC = ∠CEH [32] & ∠HCF = ∠ECH [33] (Similar Triangles)?  HF = HE [34]
004. ∠HFC = ∠CEH [32] & ∠HCF = ∠ECH [33] (Similar Triangles)?  CF = CE [35]
005. FJ = FM [16] & FJ = FN [18] ?  FN = FM [36]
006. FJ = FM [16] & FJ = FN [18] ?  F is the circumcenter of \Delta JNM [37]
007. FN = FM [36] ?  ∠FNM = ∠NMF [38]
008. FK = FO [20] & GK = GO [21] (SSS)?  ∠FKG = ∠GOF [39]
009. FK = FO [20] & GK = GO [21] ?  FG ? KO [40]
010. F,C,A are collinear [04] & G,B,A are collinear [06] & GH ? AB [07] & BD ? AC [25] & CA ? HF [05] ?  ∠HFA = ∠HGA [41]
011. ∠HFA = ∠HGA [41] ?  F,H,G,A are concyclic [42]
012. F,H,G,A are concyclic [42] ?  ∠FHA = ∠FGA [43]
013. FJ = FN [18] & GJ = GN [19] ?  JN ? FG [44]
014. J,C,A are collinear [10] & F,C,A are collinear [04] & BD ? AC [25] & JN ? FG [44] & CA ? HF [05] ?  ∠(FG-JN) = ∠HFJ [45]
015. FJ = FN [18] ?  ∠FNJ = ∠NJF [46]
016. ∠(FG-JN) = ∠HFJ [45] & ∠JNF = ∠FJN [46] ?  ∠GFH = ∠FNJ [47]
017. F,C,A are collinear [04] & AC ? FH [05] ?  AF ? FH [48]
018. H,R,A are collinear [28] & RH = RA [29] ?  R is midpoint of AH [49]
019. AF ? FH [48] & R is midpoint of AH [49] ?  HR = FR [50]
020. AF ? FH [48] & R is midpoint of AH [49] ?  AR = FR [51]
021. G,B,A are collinear [06] & GH ? AB [07] ?  HG ? GA [52]
022. HG ? GA [52] & R is midpoint of AH [49] ?  HR = GR [53]
023. HG ? GA [52] & R is midpoint of AH [49] ?  AR = GR [54]
024. HR = FR [50] & HR = GR [53] ?  RG = RF [55]
025. F,C,A are collinear [04] & G,B,A are collinear [06] & GH ? AB [07] & BD ? AC [25] & CA ? HF [05] ?  ∠HFA = ∠AGH [56]
026. F,C,A are collinear [04] & G,B,A are collinear [06] & ∠HAC = ∠BAH [01] ?  ∠HAF = ∠GAH [57]
027. ∠HFA = ∠AGH [56] & ∠HAF = ∠GAH [57] (Similar Triangles)?  HF = HG [58]
028. ∠HFA = ∠AGH [56] & ∠HAF = ∠GAH [57] (Similar Triangles)?  AF = AG [59]
029. RG = RF [55] & HF = HG [58] ?  GF ? RH [60]
030. B,S,A are collinear [30] & SB = SA [31] ?  S is midpoint of AB [61]
031. H,B,Q are collinear [26] & QH = QB [27] ?  Q is midpoint of BH [62]
032. S is midpoint of AB [61] & Q is midpoint of BH [62] ?  SQ ∥ AH [63]
033. B,S,A are collinear [30] & ∠FHA = ∠FGA [43] & G,B,A are collinear [06] & CA ? HF [05] & BD ? AC [25] & ∠GFH = ∠FNJ [47] & FG ? KO [40] & JN ? FG [44] & GF ? RH [60] & H,R,A are collinear [28] & QS ∥ AH [63] ?  ∠(FN-QS) = ∠ASQ [64]
034. ∠(FN-QS) = ∠ASQ [64] ?  FN ∥ SA [65]
035. GK = GO [21] (SSS)?  ∠GKO = ∠KOG [66]
036. J,C,A are collinear [10] & F,C,A are collinear [04] & ∠GKO = ∠KOG [66] & B,A,K are collinear [12] & G,B,A are collinear [06] & GF ? RH [60] & FG ? KO [40] & H,R,A are collinear [28] & ∠HAB = ∠CAH [01] & AH ∥ QS [63] ?  ∠(FJ-QS) = ∠(GO-QS) [67]
037. ∠(FJ-QS) = ∠(GO-QS) [67] ?  FJ ∥ GO [68]
038. J,C,A are collinear [10] & F,C,A are collinear [04] & ∠FKG = ∠GOF [39] & B,A,K are collinear [12] & G,B,A are collinear [06] & FN ∥ SA [65] & B,S,A are collinear [30] & FJ ∥ GO [68] ?  ∠NFO = ∠KFJ [69]
039. FJ = FN [18] & FK = FO [20] & ∠NFO = ∠KFJ [69] (SAS)?  ∠FNO = ∠KJF [70]
040. CA ? JB [11] & BD ? AC [25] & J,C,A are collinear [10] & B,A,K are collinear [12] & GH ? AB [07] & AB ? KC [13] ?  ∠BJC = ∠BKC [71]
041. ∠BJC = ∠BKC [71] ?  J,B,C,K are concyclic [72]
042. J,B,C,K are concyclic [72] ?  ∠JCB = ∠JKB [73]
043. FJ = FM [16] (SSS)?  ∠FJM = ∠JMF [74]
044. HF = HE [34] & CF = CE [35] ?  FE ? HC [75]
045. EJ = EM [17] & FJ = FM [16] ?  EF ? MJ [76]
046. EJ = EM [17] & FJ = FM [16] (SSS)?  ∠EMF = ∠FJE [77]
047. ∠FJM = ∠JMF [74] & J,C,A are collinear [10] & F,C,A are collinear [04] & FE ? HC [75] & FE ? JM [76] & ∠HCA = ∠BCH [00] ?  ∠(BC-JM) = ∠FMJ [78]
048. ∠(BC-JM) = ∠FMJ [78] ?  BC ∥ FM [79]
049. B,S,A are collinear [30] & P,N,O are collinear [22] & ∠FNO = ∠KJF [70] & J,C,A are collinear [10] & F,C,A are collinear [04] & ∠JCB = ∠JKB [73] & K,B,A are collinear [12] & BC ∥ FM [79] & FN ∥ SA [65] ?  ∠(FM-SA) = ∠(PN-SA) [80]
050. ∠(FM-SA) = ∠(PN-SA) [80] ?  FM ∥ PN [81]
051. P,N,O are collinear [22] & ∠FNM = ∠NMF [38] & FM ∥ PN [81] ?  ∠FNM = ∠MNP [82]
052. G,B,A are collinear [06] & GH ? AB [07] ?  HG ? GB [83]
053. HG ? GB [83] & Q is midpoint of BH [62] ?  HQ = GQ [84]
054. HG ? GB [83] & Q is midpoint of BH [62] ?  BQ = GQ [85]
055. HR = GR [53] & HQ = GQ [84] ?  HG ? RQ [86]
056. R is midpoint of AH [49] & Q is midpoint of BH [62] ?  RQ ∥ AB [87]
057. BC ? IA [08] & AD ? BC [24] & B,I,C are collinear [09] & J,C,A are collinear [10] & CA ? JB [11] & BD ? AC [25] ?  ∠AIB = ∠AJB [88]
058. ∠AIB = ∠AJB [88] ?  J,B,I,A are concyclic [89]
059. J,B,I,A are concyclic [89] ?  ∠JIB = ∠JAB [90]
060. EI = EL [14] (SSS)?  ∠ELI = ∠LIE [91]
061. EI = EL [14] & FI = FL [15] ?  IL ? EF [92]
062. F,C,A are collinear [04] & B,C,E are collinear [02] & AD ? BC [24] & BD ? AC [25] & CA ? HF [05] & BC ? HE [03] ?  ∠HFC = ∠HEC [93]
063. ∠HFC = ∠HEC [93] ?  F,H,C,E are concyclic [94]
064. F,H,C,E are concyclic [94] ?  ∠FHC = ∠FEC [95]
065. J,C,A are collinear [10] & F,C,A are collinear [04] & AC ? FH [05] ?  FJ ? FH [96]
066. FJ ? FH [96] & FE ? JM [76] ?  ∠FJM = ∠HFE [97]
067. J,C,A are collinear [10] & F,C,A are collinear [04] & ∠ELI = ∠LIE [91] & B,I,C are collinear [09] & B,C,E are collinear [02] & FE ? HC [75] & FE ? JM [76] & IL ? EF [92] & ∠FHC = ∠FEC [95] & CA ? HF [05] & BD ? AC [25] & ∠FJM = ∠HFE [97] ?  ∠FJM = ∠(LE-JM) [98]
068. ∠FJM = ∠(LE-JM) [98] ?  FJ ∥ LE [99]
069. B,I,C are collinear [09] & B,C,E are collinear [02] & ∠EMF = ∠FJE [77] & J,C,A are collinear [10] & F,C,A are collinear [04] & FJ ∥ LE [99] & FM ∥ BC [79] ?  ∠LEM = ∠JEI [100]
070. EI = EL [14] & EJ = EM [17] & ∠LEM = ∠JEI [100] (SAS)?  ∠ELM = ∠JIE [101]
071. P,M,L are collinear [23] & B,S,A are collinear [30] & ∠JIB = ∠JAB [90] & B,C,I are collinear [09] & J,C,A are collinear [10] & ∠ELM = ∠JIE [101] & B,C,E are collinear [02] & FJ ∥ LE [99] & F,C,A are collinear [04] & FJ ∥ GO [68] ?  ∠(PM-GO) = ∠(SA-GO) [102]
072. ∠(PM-GO) = ∠(SA-GO) [102] ?  PM ∥ SA [103]
073. P,M,L are collinear [23] & ∠FMN = ∠MNF [38] & HG ? RQ [86] & GH ? AB [07] & FN ∥ SA [65] & B,S,A are collinear [30] & QR ∥ AB [87] & PM ∥ SA [103] ?  ∠FMN = ∠NMP [104]
074. ∠FNM = ∠MNP [82] & ∠FMN = ∠NMP [104] (Similar Triangles)?  NF = NP [105]
075. NF = NP [105] & QG = QH [84] ?  NF:NP = QG:QH [106]
076. B,S,A are collinear [30] & J,C,A are collinear [10] & F,C,A are collinear [04] & ∠JCB = ∠JKB [73] & K,B,A are collinear [12] ?  ∠(SA-JK) = ∠(BC-FJ) [107]
077. G,B,A are collinear [06] & B,C,E are collinear [02] & AD ? BC [24] & GH ? AB [07] & BC ? HE [03] ?  ∠HGB = ∠HEB [108]
078. ∠HGB = ∠HEB [108] ?  G,H,B,E are concyclic [109]
079. G,H,B,E are concyclic [109] ?  ∠GHB = ∠GEB [110]
080. G,H,B,E are concyclic [109] ?  ∠GBH = ∠GEH [111]
081. HF = HE [34] & HF = HG [58] ?  HG = HE [112]
082. HF = HE [34] & HF = HG [58] ?  H is the circumcenter of \Delta FGE [113]
083. HG = HE [112] ?  ∠HGE = ∠GEH [114]
084. BQ = GQ [85] ?  ∠QGB = ∠GBQ [115]
085. B,S,A are collinear [30] & ∠GHB = ∠GEB [110] & B,C,E are collinear [02] & ∠HGE = ∠GEH [114] & BC ? HE [03] & AD ? BC [24] & ∠GBH = ∠GEH [111] & G,B,A are collinear [06] & ∠QGB = ∠GBQ [115] & H,B,Q are collinear [26] ?  ∠(SA-GQ) = ∠CBH [116]
086. ∠(SA-JK) = ∠(BC-FJ) [107] & ∠(SA-GQ) = ∠CBH [116] ?  ∠(FJ-HB) = ∠(JK-GQ) [117]
087. P,N,O are collinear [22] & H,B,Q are collinear [26] & ∠(FJ-HB) = ∠(JK-GQ) [117] & J,C,A are collinear [10] & F,C,A are collinear [04] & ∠FNO = ∠KJF [70] ?  ∠FNP = ∠GQH [118]
088. NF:NP = QG:QH [106] & ∠FNP = ∠GQH [118] (Similar Triangles)?  FN:FP = GQ:GH [119]
089. FN:FP = GQ:GH [119] & GH = EH [112] & FJ = FN [18] & HQ = GQ [84] & FH = HE [34] ?  FJ:FP = HQ:HF [120]
090. B,C,E are collinear [02] & BC ? EH [03] ?  BE ? EH [121]
091. BE ? EH [121] & Q is midpoint of BH [62] ?  HQ = EQ [122]
092. HQ = EQ [122] & HQ = GQ [84] ?  QG = QE [123]
093. QG = QE [123] & HG = HE [112] ?  GE ? QH [124]
094. GE ? QH [124] & H,B,Q are collinear [26] ?  EG ? BH [125]
095. FJ ? FH [96] & EG ? BH [125] ?  ∠(FJ-GE) = ∠FHB [126]
096. P,M,L are collinear [23] & P,N,O are collinear [22] & ∠FNM = ∠NMF [38] & HG ? RQ [86] & GH ? AB [07] & FN ∥ SA [65] & B,S,A are collinear [30] & QR ∥ AB [87] & PM ∥ SA [103] & FM ∥ PN [81] ?  ∠PMN = ∠MNP [127]
097. ∠PMN = ∠MNP [127] ?  PM = PN [128]
098. FN = FM [36] & PM = PN [128] ?  NM ? FP [129]
099. J,C,A are collinear [10] & F,C,A are collinear [04] & IL ? EF [92] & BD ? AC [25] & CA ? HF [05] & EF ? MJ [76] ?  ∠JFH = ∠(FE-JM) [130]
100. J,C,A are collinear [10] & F,C,A are collinear [04] & CA ? JB [11] & BD ? AC [25] ?  FJ ? JB [131]
101. F is the circumcenter of \Delta JNM [37] & FJ ? JB [131] ?  ∠BJN = ∠JMN [132]
102. ∠BJN = ∠JMN [132] & CA ? JB [11] & BD ? AC [25] & CA ? HF [05] ?  ∠(FH-JN) = ∠JMN [133]
103. ∠JFH = ∠(FE-JM) [130] & ∠(FH-JN) = ∠JMN [133] ?  ∠FJN = ∠(FE-MN) [134]
104. J,C,A are collinear [10] & F,C,A are collinear [04] & ∠FNJ = ∠NJF [46] & GF ? RH [60] & FG ? KO [40] & H,R,A are collinear [28] & JN ? FG [44] & ∠FJN = ∠(FE-MN) [134] & AH ∥ QS [63] ?  ∠(FE-MN) = ∠(FJ-QS) [135]
105. H is the circumcenter of \Delta FGE [113] & FJ ? FH [96] ?  ∠JFG = ∠FEG [136]
106. ∠(FE-MN) = ∠(FJ-QS) [135] & ∠GFJ = ∠GEF [136] ?  ∠(QS-FG) = ∠(MN-EG) [137]
107. JN ? FG [44] & FG ? KO [40] & GF ? RH [60] & H,R,A are collinear [28] & QS ∥ AH [63] ?  ∠(QS-FG) = ∠(FG-QS) [138]
108. ∠FJN = ∠(FE-MN) [134] & J,C,A are collinear [10] & F,C,A are collinear [04] & ∠JFG = ∠FEG [136] & FG ? KO [40] & JN ? FG [44] & GF ? RH [60] & H,R,A are collinear [28] & QS ∥ AH [63] ?  ∠FGE = ∠(QS-MN) [139]
109. ∠(QS-FG) = ∠(FG-QS) [138] & ∠FGE = ∠(QS-MN) [139] ?  ∠(QS-FG) = ∠(EG-MN) [140]
110. J,C,A are collinear [10] & F,C,A are collinear [04] & H,B,Q are collinear [26] & ∠(FJ-GE) = ∠FHB [126] & CA ? HF [05] & BD ? AC [25] & NM ? FP [129] & EG ? BH [125] & GE ? QH [124] & ∠(QS-FG) = ∠(MN-EG) [137] & FG ? KO [40] & JN ? FG [44] & GF ? RH [60] & H,R,A are collinear [28] & QS ∥ AH [63] & ∠(QS-FG) = ∠(EG-MN) [140] ?  ∠JFP = ∠FHQ [141]
111. FJ:FP = HQ:HF [120] & ∠JFP = ∠FHQ [141] (Similar Triangles)?  PJ:FQ = PF:FH [142]
112. FJ:FP = HQ:HF [120] & ∠JFP = ∠FHQ [141] (Similar Triangles)?  ∠FJP = ∠FQH [143]
113. FJ:FP = HQ:HF [120] & ∠JFP = ∠FHQ [141] (Similar Triangles)?  ∠JPF = ∠HFQ [144]
114. B,S,A are collinear [30] & H,R,A are collinear [28] & AH ∥ QS [63] & AB ∥ QR [87] ?  ∠ASQ = ∠QRA [145]
115. H,R,A are collinear [28] & QS ∥ AH [63] ?  ∠AQS = ∠QAR [146]
116. ∠ASQ = ∠QRA [145] & ∠AQS = ∠QAR [146] (Similar Triangles)?  AS = QR [147]
117. ∠ASQ = ∠QRA [145] & ∠AQS = ∠QAR [146] (Similar Triangles)?  QS = AR [148]
118. J,C,A are collinear [10] & CA ? JB [11] & BD ? AC [25] ?  AJ ? JB [149]
119. AJ ? JB [149] & S is midpoint of AB [61] ?  AS = JS [150]
120. AS = QR [147] & AS = JS [150] ?  JS = QR [151]
121. AR = FR [51] & QS = AR [148] ?  SQ = RF [152]
122. B,S,A are collinear [30] & J,C,A are collinear [10] & F,C,A are collinear [04] & ∠BAH = ∠HAC [01] & AH ∥ QS [63] ?  ∠ASQ = ∠(QS-FJ) [153]
123. AS = JS [150] ?  ∠SJA = ∠JAS [154]
124. AR = GR [54] & AR = FR [51] & AF = AG [59] (SSS)?  ∠GAR = ∠AFR [155]
125. J,C,A are collinear [10] & F,C,A are collinear [04] & ∠SJA = ∠JAS [154] & B,S,A are collinear [30] & ∠GAR = ∠AFR [155] & G,B,A are collinear [06] & H,R,A are collinear [28] & AH ∥ QS [63] ?  ∠(QS-FR) = ∠FJS [156]
126. ∠ASQ = ∠(QS-FJ) [153] & ∠(QS-FR) = ∠FJS [156] ?  ∠QSJ = ∠(SA-FR) [157]
127. ∠QSJ = ∠(SA-FR) [157] & B,S,A are collinear [30] & QS ∥ AH [63] & FN ∥ SA [65] & AB ∥ QR [87] ?  ∠JSQ = ∠FRQ [158]
128. JS = QR [151] & SQ = RF [152] & ∠JSQ = ∠FRQ [158] (SAS)?  QJ = FQ [159]
129. PJ:FQ = PF:FH [142] & HF = HE [34] & JQ = FQ [159] ?  JQ:JP = FH:FP [160]
130. J,C,A are collinear [10] & F,C,A are collinear [04] & BD ? AC [25] & JN ? FG [44] & CA ? HF [05] ?  ∠JFH = ∠(FG-JN) [161]
131. ∠BJN = ∠JMN [132] & CA ? JB [11] & BD ? AC [25] & CA ? HF [05] ?  ∠(FH-JM) = ∠JNM [162]
132. ∠JFH = ∠(FG-JN) [161] & ∠(FH-JM) = ∠JNM [162] ?  ∠FJM = ∠(FG-MN) [163]
133. ∠JFG = ∠FEG [136] & J,C,A are collinear [10] & F,C,A are collinear [04] & ∠FJM = ∠(FG-MN) [163] ?  ∠JMN = ∠FEG [164]
134. ∠HFE = ∠FJM [97] & ∠JMN = ∠FEG [164] ?  ∠(FH-GE) = ∠(FJ-MN) [165]
135. ∠(FH-GE) = ∠(FJ-MN) [165] & J,C,A are collinear [10] & F,C,A are collinear [04] & CA ? HF [05] & BD ? AC [25] & FJ ∥ GO [68] & NM ? FP [129] & EG ? BH [125] & GE ? QH [124] & ∠(QS-FG) = ∠(MN-EG) [137] & FG ? KO [40] & JN ? FG [44] & GF ? RH [60] & H,R,A are collinear [28] & QS ∥ AH [63] & ∠(QS-FG) = ∠(EG-MN) [140] & H,B,Q are collinear [26] ?  ∠(FH-GO) = ∠(FP-MN) [166]
136. QJ = FQ [159] ?  ∠QFJ = ∠FJQ [167]
137. ∠FJP = ∠FQH [143] & J,C,A are collinear [10] & F,C,A are collinear [04] & H,B,Q are collinear [26] & ∠QFJ = ∠FJQ [167] & FJ ∥ GO [68] & GE ? QH [124] & ∠(QS-FG) = ∠(MN-EG) [137] & FG ? KO [40] & JN ? FG [44] & GF ? RH [60] & H,R,A are collinear [28] & QS ∥ AH [63] & ∠(QS-FG) = ∠(EG-MN) [140] ?  ∠(GO-JQ) = ∠(MN-PJ) [168]
138. ∠(FH-GO) = ∠(FP-MN) [166] & ∠(GO-JQ) = ∠(MN-PJ) [168] ?  ∠HFP = ∠QJP [169]
139. JQ:JP = FH:FP [160] & ∠QJP = ∠HFP [169] (Similar Triangles)?  QJ:HF = QP:HP [170]
140. JQ:JP = FH:FP [160] & ∠QJP = ∠HFP [169] (Similar Triangles)?  ∠HPQ = ∠FPJ [171]
141. QJ:HF = QP:HP [170] & QJ = FQ [159] & HF = HE [34] ?  FQ:FH = PQ:PH [172]
142. ∠HPQ = ∠FPJ [171] & ∠JPF = ∠HFQ [144] & CA ? HF [05] & BD ? AC [25] ?  ∠QFH = ∠HPQ [173]
143. FQ:FH = PQ:PH [172] & ∠QFH = ∠HPQ [173] (Similar Triangles)?  HF = HP [174]
144. HF = HE [34] & HF = HP [174] ?  HP = HE
==========================

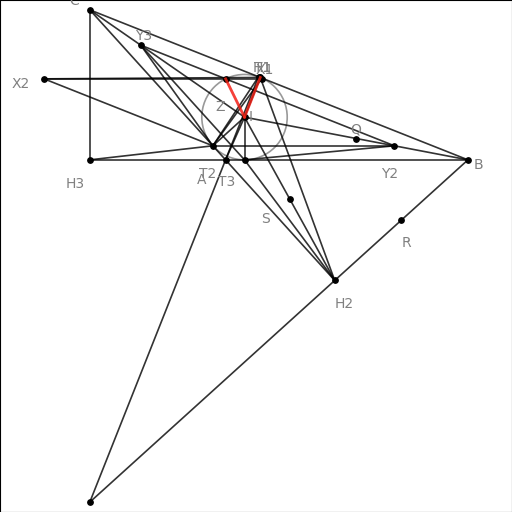
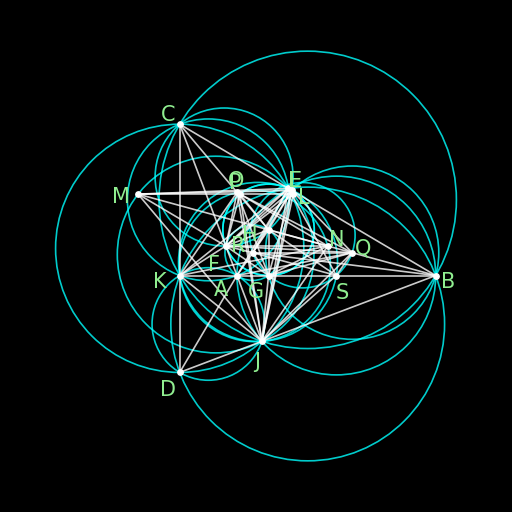
生成的图如下：圆还是让人眼花。。。还是需要我们自己用tkz来画。。如果有相关插件可能是个很不错的想法。


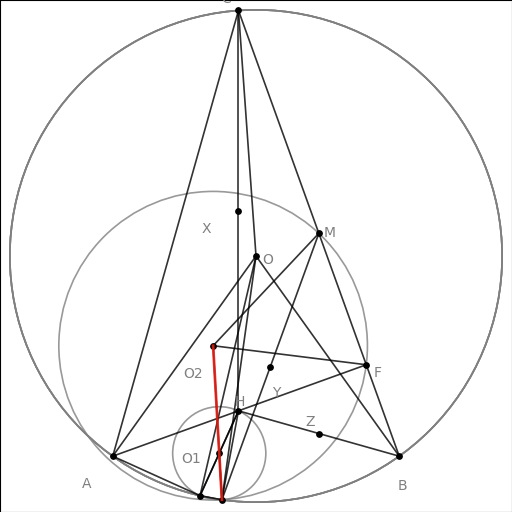
IMO 2015 P3




alphageometry生成的证明如下：

==========================
 * From theorem premises:
A B C D E F G H I J K : Points
AD ? BC [00]
BD ? AC [01]
C,B,E are collinear [02]
A,E,D are collinear [03]
C,B,F are collinear [04]
FB = FC [05]
GB = GC [06]
GA = GB [07]
AH ? DH [08]
GH = GA [09]
GI = GA [10]
DI ? HI [11]
JI = JH [12]
JH = JD [13]
CF:JH = CF:JH [14]
KE = KI [15]
KI = KF [16]

 * Auxiliary Constructions:
L M N : Points
B,A,L are collinear [17]
LB = LA [18]
C,A,M are collinear [19]
MC = MA [20]
∠NLF = ∠LFN [21]
∠NML = ∠MLN [22]
NL = NF [23]
NM = NL [24]

 * Proof steps:
001. GB = GC [06] & GA = GB [07] & GI = GA [10] & GH = GA [09] ?  C,A,I,H are concyclic [25]
002. C,I,A,H are concyclic [25] ?  ∠CAI = ∠CHI [26]
003. C,I,A,H are concyclic [25] ?  ∠CIA = ∠CHA [27]
004. GB = GC [06] & GA = GB [07] & GH = GA [09] ?  GH = GC [28]
005. C,A,I,H are concyclic [25] & GB = GC [06] & GA = GB [07] & GH = GA [09] ?  B,A,C,I are concyclic [29]
006. B,A,C,I are concyclic [29] ?  ∠CIA = ∠CBA [30]
007. C,A,I,H are concyclic [25] & B,A,C,I are concyclic [29] ?  C,I,H,B are concyclic [31]
008. C,I,H,B are concyclic [31] ?  ∠CIH = ∠CBH [32]
009. C,B,F are collinear [04] & FB = FC [05] ?  F is midpoint of CB [33]
010. B,A,L are collinear [17] & LB = LA [18] ?  L is midpoint of BA [34]
011. F is midpoint of CB [33] & L is midpoint of BA [34] ?  FL ∥ CA [35]
012. C,A,M are collinear [19] & MC = MA [20] ?  M is midpoint of CA [36]
013. M is midpoint of CA [36] & L is midpoint of BA [34] ?  ML ∥ CB [37]
014. GH = GC [28] ?  ∠GHC = ∠HCG [38]
015. GA = GB [07] & GH = GA [09] ?  GH = GB [39]
016. GH = GB [39] ?  ∠GHB = ∠HBG [40]
017. GB = GC [06] ?  ∠GCB = ∠CBG [41]
018. ∠GCB = ∠CBG [41] & LM ∥ BC [37] ?  ∠(CG-LM) = ∠(LM-BG) [42]
019. KE = KI [15] ?  ∠KIE = ∠IEK [43]
020. KI = KF [16] ?  ∠KIF = ∠IFK [44]
021. KI = KF [16] & KE = KI [15] ?  KE = KF [45]
022. KE = KF [45] ?  ∠KEF = ∠EFK [46]
023. ∠KEF = ∠EFK [46] & C,B,F are collinear [04] & C,B,E are collinear [02] & LM ∥ BC [37] ?  ∠(EK-LM) = ∠(LM-FK) [47]
024. NL = NF [23] & NM = NL [24] ?  NM = NF [48]
025. NM = NF [48] ?  ∠NMF = ∠MFN [49]
026. F is midpoint of CB [33] & M is midpoint of CA [36] ?  FM ∥ BA [50]
027. ∠NMF = ∠MFN [49] & FM ∥ AB [50] ?  ∠(MN-AB) = ∠(AB-FN) [51]
028. GI = GA [10] & GH = GA [09] ?  GH = GI [52]
029. GH = GI [52] & JI = JH [12] (SSS)?  ∠GHJ = ∠JIG [53]
030. JH = JD [13] & JI = JH [12] ?  J is the circumcenter of \Delta HDI [54]
031. DI ? HI [11] & AH ? DH [08] ?  ∠AHD = ∠HID [55]
032. J is the circumcenter of \Delta HDI [54] & ∠AHD = ∠HID [55] ?  HA ? JH [56]
033. HA ? JH [56] & AH ? DH [08] ?  J,D,H are collinear [57]
034. ∠GHJ = ∠JIG [53] & J,D,H are collinear [57] ?  ∠GHD = ∠JIG [58]
035. J,D,H are collinear [57] & JH = JD [13] ?  J is midpoint of HD [59]
036. M is midpoint of CA [36] & J is midpoint of HD [59] ?  MC:JD = CA:DH [60]
037. C,B,E are collinear [02] & A,E,D are collinear [03] & BC ? AD [00] ?  CE ? EA [61]
038. CE ? EA [61] & M is midpoint of CA [36] ?  CM = EM [62]
039. CE ? EA [61] & M is midpoint of CA [36] ?  AM = EM [63]
040. MC:JD = CA:DH [60] & CM = EM [62] & JH = JD [13] ?  EM:JH = CA:DH [64]
041. A,E,D are collinear [03] & C,B,E are collinear [02] & AD ? BC [00] ?  ∠AEC = ∠BED [65]
042. A,E,D are collinear [03] & BC ? AD [00] ?  CB ? AE [66]
043. BD ? AC [01] & CB ? AE [66] ?  ∠CAE = ∠DBC [67]
044. A,E,D are collinear [03] & C,B,E are collinear [02] & ∠CAE = ∠DBC [67] ?  ∠CAE = ∠DBE [68]
045. ∠AEC = ∠BED [65] & ∠CAE = ∠DBE [68] (Similar Triangles)?  CA:BD = AE:BE [69]
046. GA = GB [07] & GB = GC [06] ?  GC = GA [70]
047. GA = GB [07] & GB = GC [06] ?  G is the circumcenter of \Delta CBA [71]
048. GC = GA [70] & MC = MA [20] ?  CA ? GM [72]
049. C,B,E are collinear [02] & A,E,D are collinear [03] & C,A,M are collinear [19] & ∠CAE = ∠DBC [67] & CA ? GM [72] & BD ? AC [01] & AC ∥ FL [35] ?  ∠BEA = ∠GMA [73]
050. GC = GA [70] ?  ∠GCA = ∠CAG [74]
051. G is the circumcenter of \Delta CBA [71] & F is midpoint of CB [33] ?  ∠ACG = ∠(AB-FG) [75]
052. FB = FC [05] & GB = GC [06] ?  BC ? FG [76]
053. A,E,D are collinear [03] & C,A,M are collinear [19] & ∠GCA = ∠CAG [74] & FL ∥ AC [35] & ∠ACG = ∠(AB-FG) [75] & BC ? FG [76] & AD ? BC [00] & BC ∥ LM [37] ?  ∠BAE = ∠GAM [77]
054. ∠BEA = ∠GMA [73] & ∠BAE = ∠GAM [77] (Similar Triangles)?  EB:EA = MG:MA [78]
055. CA:BD = AE:BE [69] & EB:EA = MG:MA [78] & AM = EM [63] ?  EM:MG = CA:BD [79]
056. EM:JH = CA:DH [64] & EM:MG = CA:BD [79] ?  DH:BD = JH:MG [80]
057. GH = GA [09] ?  ∠GHA = ∠HAG [81]
058. ∠NLF = ∠LFN [21] & ∠NML = ∠MLN [22] & ∠CAI = ∠CHI [26] & ∠CIA = ∠CHA [27] & ∠CIA = ∠CBA [30] & ∠CIH = ∠CBH [32] & FL ∥ AC [35] & LM ∥ BC [37] & ∠GHC = ∠HCG [38] & ∠GHB = ∠HBG [40] & ∠GHA = ∠HAG [81] & ∠(CG-LM) = ∠(LM-BG) [42] & ∠(MN-AB) = ∠(AB-FN) [51] (Angle chase)?  FN ∥ AG [82]
059. FL ∥ AC [35] & AG ∥ FN [82] ?  ∠CAG = ∠LFN [83]
060. ∠NLF = ∠LFN [21] & ∠NML = ∠MLN [22] & ∠CAI = ∠CHI [26] & ∠CIA = ∠CBA [30] & ∠CIH = ∠CBH [32] & FL ∥ AC [35] & ∠GHC = ∠HCG [38] & ∠GHB = ∠HBG [40] & ∠(CG-LM) = ∠(LM-BG) [42] & ∠(MN-AB) = ∠(AB-FN) [51] (Angle chase)?  LN ∥ CG [84]
061. ∠NLF = ∠LFN [21] & ∠NML = ∠MLN [22] & ∠CAI = ∠CHI [26] & ∠CIA = ∠CBA [30] & ∠CIH = ∠CBH [32] & FL ∥ AC [35] & ∠GHC = ∠HCG [38] & ∠GHB = ∠HBG [40] & ∠(CG-LM) = ∠(LM-BG) [42] & ∠(MN-AB) = ∠(AB-FN) [51] (Angle chase)?  MN ∥ BG [85]
062. CG ∥ LN [84] & AG ∥ FN [82] ?  ∠CGA = ∠LNF [86]
063. ∠CAG = ∠LFN [83] & ∠CGA = ∠LNF [86] (Similar Triangles)?  CA:CG = LF:LN [87]
064. C,A,M are collinear [19] & C,B,F are collinear [04] & BC ∥ LM [37] & AC ∥ FL [35] ?  ∠CML = ∠LFC [88]
065. C,B,F are collinear [04] & LM ∥ BC [37] ?  ∠CLM = ∠LCF [89]
066. ∠CML = ∠LFC [88] & ∠CLM = ∠LCF [89] (Similar Triangles)?  CM = LF [90]
067. CM = LF [90] & CM = EM [62] ?  EM = LF [91]
068. G is the circumcenter of \Delta CBA [71] & L is midpoint of BA [34] ?  ∠ACB = ∠AGL [92]
069. G is the circumcenter of \Delta CBA [71] & L is midpoint of BA [34] ?  ∠BCA = ∠BGL [93]
070. ∠BCA = ∠LGA [92] & AC ∥ FL [35] ?  ∠(CB-LF) = ∠LGA [94]
071. CM = EM [62] ?  ∠MEC = ∠ECM [95]
072. ∠MEC = ∠ECM [95] & C,B,E are collinear [02] & C,A,M are collinear [19] & LM ∥ BC [37] & FL ∥ AC [35] ?  ∠LME = ∠ACB [96]
073. ∠ACB = ∠LGB [93] & ∠LME = ∠ACB [96] & LM ∥ BC [37] ?  ∠(CB-EM) = ∠LGB [97]
074. ∠(CB-LF) = ∠LGA [94] & ∠(CB-EM) = ∠LGB [97] ?  ∠(AG-FL) = ∠(BG-EM) [98]
075. ∠(BG-EM) = ∠(AG-FL) [98] & BG ∥ MN [85] & AG ∥ FN [82] ?  ∠NME = ∠NFL [99]
076. NM = NF [48] & EM = LF [91] & ∠NME = ∠NFL [99] (SAS)?  EN = LN [100]
077. CA:CG = LF:LN [87] & GI = GA [10] & GA = GB [07] & GB = GC [06] & EN = LN [100] & EM = LF [91] & HG = IG [52] ?  EM:LN = CA:HG [101]
078. EM:MG = CA:BD [79] & EM:LN = CA:HG [101] ?  BD:HG = MG:LN [102]
079. C,B,E are collinear [02] & A,E,D are collinear [03] & BC ? AD [00] ?  BE ? EA [103]
080. BE ? EA [103] & L is midpoint of BA [34] ?  AL = EL [104]
081. BE ? EA [103] & L is midpoint of BA [34] ?  BL = EL [105]
082. C,A,M are collinear [19] & BC ∥ LM [37] & AC ∥ FL [35] ?  ∠AML = ∠FLM [106]
083. B,A,L are collinear [17] & BC ∥ LM [37] & AB ∥ FM [50] ?  ∠ALM = ∠FML [107]
084. ∠AML = ∠FLM [106] & ∠ALM = ∠FML [107] (Similar Triangles)?  LA = MF [108]
085. AL = EL [104] & LA = MF [108] ?  MF = LE [109]
086. BL = EL [105] ?  ∠LBE = ∠BEL [110]
087. G is the circumcenter of \Delta CBA [71] & M is midpoint of CA [36] ?  ∠CBA = ∠CGM [111]
088. G is the circumcenter of \Delta CBA [71] & M is midpoint of CA [36] ?  ∠BCG = ∠(AB-GM) [112]
089. ∠LBE = ∠BEL [110] & B,A,L are collinear [17] & C,B,E are collinear [02] & LM ∥ BC [37] & ∠ABC = ∠MGC [111] ?  ∠MGC = ∠(CB-LE) [113]
090. ∠(CG-LM) = ∠(LM-BG) [42] & ∠BCG = ∠(AB-GM) [112] & LM ∥ BC [37] & AB ∥ FM [50] ?  ∠GMF = ∠CBG [114]
091. ∠MGC = ∠(CB-LE) [113] & ∠GMF = ∠CBG [114] ?  ∠(CG-EL) = ∠(FM-BG) [115]
092. ∠(CG-EL) = ∠(FM-BG) [115] & FM ∥ AB [50] & CG ∥ LN [84] & BG ∥ MN [85] ?  ∠NLE = ∠FMN [116]
093. NM = NL [24] & MF = LE [109] & ∠NLE = ∠FMN [116] (SAS)?  EN = FN [117]
094. BD:HG = MG:LN [102] & HG = IG [52] & EN = LN [100] & HG = CG [28] & AG = CG [70] & GA = GB [07] & EN = FN [117] & NL = NF [23] & NM = NL [24] ?  BD:BG = MG:MN [118]
095. CA ? GM [72] & BD ? AC [01] & AC ∥ FL [35] & BG ∥ MN [85] ?  ∠DBG = ∠GMN [119]
096. BD:BG = MG:MN [118] & ∠DBG = ∠GMN [119] (Similar Triangles)?  BD:DG = MG:NG [120]
097. BD:BG = MG:MN [118] & ∠DBG = ∠GMN [119] (Similar Triangles)?  ∠(BD-GM) = ∠DGN [121]
098. DH:BD = JH:MG [80] & BD:DG = MG:NG [120] ?  DH:JH = DG:NG [122]
099. ∠(BD-GM) = ∠DGN [121] & CA ? GM [72] & BD ? AC [01] & AC ∥ FL [35] ?  DG ∥ GN [123]
100. DG ∥ GN [123] ?  N,D,G are collinear [124]
101. DH:JH = DG:NG [122] & N,D,G are collinear [124] & J,D,H are collinear [57] ?  GH ∥ NJ [125]
102. GH ∥ JN [125] & J,D,H are collinear [57] & N,D,G are collinear [124] ?  DJ:JN = DH:HG [126]
103. F is midpoint of CB [33] & J is midpoint of HD [59] ?  FC:JD = CB:DH [127]
104. FC:JD = CB:DH [127] & JH = JD [13] ?  CF:JH = CB:DH [128]
105. MN ∥ BG [85] & LM ∥ BC [37] ?  ∠GBC = ∠NML [129]
106. LN ∥ CG [84] & LM ∥ BC [37] ?  ∠GCB = ∠NLM [130]
107. ∠GBC = ∠NML [129] & ∠GCB = ∠NLM [130] (Similar Triangles)?  BG:BC = MN:ML [131]
108. C,A,M are collinear [19] & C,B,F are collinear [04] & BC ∥ LM [37] & AC ∥ FL [35] ?  ∠AML = ∠LFB [132]
109. B,A,L are collinear [17] & C,B,F are collinear [04] & BC ∥ LM [37] ?  ∠ALM = ∠LBF [133]
110. ∠AML = ∠LFB [132] & ∠ALM = ∠LBF [133] (Similar Triangles)?  LA:BL = LM:BF [134]
111. BG:BC = MN:ML [131] & HG = IG [52] & HG = CG [28] & AG = CG [70] & GA = GB [07] & EN = FN [117] & NL = NF [23] & NM = NL [24] & LA:BL = LM:BF [134] & LB = LA [18] & FB = FC [05] & LN = EN [100] ?  CF:LN = CB:HG [135]
112. CF:JH = CB:DH [128] & CF:LN = CB:HG [135] ?  JH:LN = DH:HG [136]
113. DJ:JN = DH:HG [126] & JH = JD [13] & HG = IG [52] & JH:LN = DH:HG [136] & EN = LN [100] ?  JH:LN = JH:JN [137]
114. CF:JH = CF:JH [14] & JH:LN = JH:JN [137] ?  LN = JN [138]
115. LN = JN [138] & EN = LN [100] & EN = FN [117] & NL = NF [23] & NM = NL [24] ?  E,J,F,M are concyclic [139]
116. E,J,F,M are concyclic [139] ?  ∠EJF = ∠EMF [140]
117. E,J,F,M are concyclic [139] ?  ∠EFJ = ∠EMJ [141]
118. ∠EJF = ∠EMF [140] & FM ∥ AB [50] ?  ∠EJF = ∠(EM-AB) [142]
119. ∠EFJ = ∠EMJ [141] & C,B,F are collinear [04] & C,B,E are collinear [02] & LM ∥ BC [37] ?  ∠(LM-FJ) = ∠EMJ [143]
120. LN = JN [138] & NM = NL [24] ?  NM = NJ [144]
121. NM = NJ [144] ?  ∠NMJ = ∠MJN [145]
122. ∠NMJ = ∠MJN [145] & GH ∥ JN [125] ?  ∠NMJ = ∠(JM-GH) [146]
123. ∠NLF = ∠LFN [21] & ∠NML = ∠MLN [22] & ∠CAI = ∠CHI [26] & ∠CIA = ∠CHA [27] & ∠CIA = ∠CBA [30] & ∠CIH = ∠CBH [32] & FL ∥ AC [35] & ∠GHC = ∠HCG [38] & ∠GHB = ∠HBG [40] & ∠(CG-LM) = ∠(LM-BG) [42] & ∠(MN-AB) = ∠(AB-FN) [51] & ∠EML = ∠BCA [96] & ∠(LM-FJ) = ∠EMJ [143] & ∠NMJ = ∠(JM-GH) [146] (Angle chase)?  AH ? FJ [147]
124. GA = GB [07] & LB = LA [18] ?  AB ? GL [148]
125. AB ? GL [148] & AB ∥ FM [50] ?  LG ? FM [149]
126. CB ? FG [76] & LG ? FM [149] ?  ∠(BC-FM) = ∠FGL [150]
127. ∠(BC-FM) = ∠FGL [150] & LM ∥ BC [37] & FM ∥ AB [50] & ∠LBE = ∠BEL [110] & B,A,L are collinear [17] & C,B,E are collinear [02] ?  ∠(CB-LE) = ∠LGF [151]
128. ∠(CB-LF) = ∠LGA [94] & ∠(CB-LE) = ∠LGF [151] ?  ∠(FL-AG) = ∠(EL-FG) [152]
129. ∠(EL-FG) = ∠(FL-AG) [152] & AG ∥ FN [82] ?  ∠(LE-FG) = ∠LFN [153]
130. C,B,F are collinear [04] & C,B,E are collinear [02] & ∠LME = ∠ACB [96] & LM ∥ BC [37] & AC ∥ FL [35] ?  ∠FEM = ∠FLM [154]
131. ∠FEM = ∠FLM [154] ?  L,E,F,M are concyclic [155]
132. E,J,F,M are concyclic [139] & L,E,F,M are concyclic [155] ?  L,E,J,F are concyclic [156]
133. L,E,J,F are concyclic [156] ?  ∠JEL = ∠JFL [157]
134. ∠(LE-FG) = ∠LFN [153] & ∠JEL = ∠JFL [157] ?  ∠NFG = ∠FJE [158]
135. AH ? FJ [147] & AH ? DH [08] & J,D,H are collinear [57] & ∠NFG = ∠FJE [158] & FN ∥ AG [82] ?  ∠EJH = ∠FGA [159]
136. AH ? DH [08] & CB ? AE [66] ?  ∠HAE = ∠(DH-CB) [160]
137. C,B,F are collinear [04] & C,B,E are collinear [02] & A,E,D are collinear [03] & AH ? FJ [147] & AH ? DH [08] & J,D,H are collinear [57] & ∠HAE = ∠(DH-CB) [160] ?  ∠FEA = ∠FHA [161]
138. ∠FEA = ∠FHA [161] ?  A,E,F,H are concyclic [162]
139. A,E,F,H are concyclic [162] ?  ∠AEH = ∠AFH [163]
140. AH ? FJ [147] & AH ? DH [08] & J,D,H are collinear [57] & ∠AEH = ∠AFH [163] & A,E,D are collinear [03] & BC ? FG [76] & AD ? BC [00] & BC ∥ LM [37] ?  ∠EHJ = ∠GFA [164]
141. ∠EJH = ∠FGA [159] & ∠EHJ = ∠GFA [164] (Similar Triangles)?  JE:JH = GA:GF [165]
142. JE:JH = GA:GF [165] & GI = GA [10] & JI = JH [12] ?  GI:GF = JE:JI [166]
143. AH ? FJ [147] & AH ? DH [08] & J,D,H are collinear [57] & ∠GHJ = ∠JIG [53] & GH ∥ JN [125] ?  ∠NJI = ∠(JF-IG) [167]
144. NL = NF [23] & LN = JN [138] ?  NJ = NF [168]
145. NJ = NF [168] ?  ∠NJF = ∠JFN [169]
146. ∠FJE = ∠NFG [158] & ∠FJN = ∠NFJ [169] ?  ∠GFJ = ∠EJN [170]
147. ∠NJI = ∠(JF-IG) [167] & ∠GFJ = ∠EJN [170] ?  ∠IGF = ∠IJE [171]
148. GI:GF = JE:JI [166] & ∠IGF = ∠IJE [171] (Similar Triangles)?  ∠GIF = ∠IEJ [172]
149. AH ? DH [08] & ∠NLF = ∠LFN [21] & ∠NML = ∠MLN [22] & ∠CAI = ∠CHI [26] & ∠CIA = ∠CHA [27] & ∠CIA = ∠CBA [30] & ∠CIH = ∠CBH [32] & FL ∥ AC [35] & LM ∥ BC [37] & ∠GHC = ∠HCG [38] & ∠GHB = ∠HBG [40] & ∠(CG-LM) = ∠(LM-BG) [42] & ∠KIE = ∠IEK [43] & ∠KIF = ∠IFK [44] & ∠(EK-LM) = ∠(LM-FK) [47] & ∠(MN-AB) = ∠(AB-FN) [51] & ∠GHD = ∠JIG [58] & ∠EJF = ∠(EM-AB) [142] & ∠(LM-FJ) = ∠EMJ [143] & ∠NMJ = ∠(JM-GH) [146] & ∠GIF = ∠IEJ [172] (Angle chase)?  IJ ∥ IK [173]
150. IJ ∥ IK [173] ?  J,I,K are collinear
==========================

在自定义问题上的测试
结论：简单问题可以迅速得到结果，不是所有问题都能转化为alphageometry的输入。
圆幂定理
我们首先选择了一个比较简单的问题，圆幂定理的一种情形：
如图，ABCE为圆D上四点，且四边形ABCE的外接圆的圆心D在其内部，CE与BA不平行，CE交BA与F，则 FE\cdot FC=FA\cdot FB


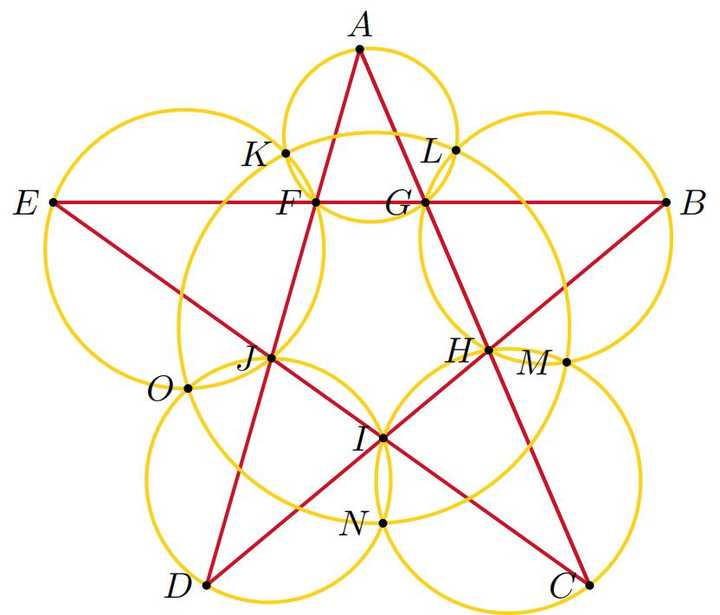
我们将其转换为alphageometry可以识别的输入：

a b c = triangle a b c; d = circle d a b c; e = on_circle e d a; f = intersection_ll f a e c b ? eqratio f e f b f c f a

这个问题很简单，我们直接就能看出来一堆相似三角形，同样，alphageometry在没有需要构造的情况下就给出了证明：

==========================
 * From theorem premises:
A B C D E F : Points
DA = DB [00]
DB = DC [01]
DE = DA [02]
E,A,F are collinear [03]
C,B,F are collinear [04]

 * Auxiliary Constructions:
: Points


 * Proof steps:
001. DA = DB [00] & DE = DA [02] & DB = DC [01] ?  C,E,B,A are concyclic [05]
002. C,E,B,A are concyclic [05] ?  ∠CBE = ∠CAE [06]
003. E,A,F are collinear [03] & C,B,F are collinear [04] & ∠CAE = ∠CBE [06] ?  ∠CAF = ∠FBE [07]
004. C,B,F are collinear [04] & E,A,F are collinear [03] ?  ∠CFA = ∠BFE [08]
005. ∠CAF = ∠FBE [07] & ∠CFA = ∠BFE [08] (Similar Triangles)?  CF:AF = EF:BF
==========================

五点共圆
这道题目非常有名。题目如下：
如图，五角星ABCDE的每个角对应的三角形的外接圆分别交于 K,L,M,N,O 求证 K,L,M,N,O 五点共圆。


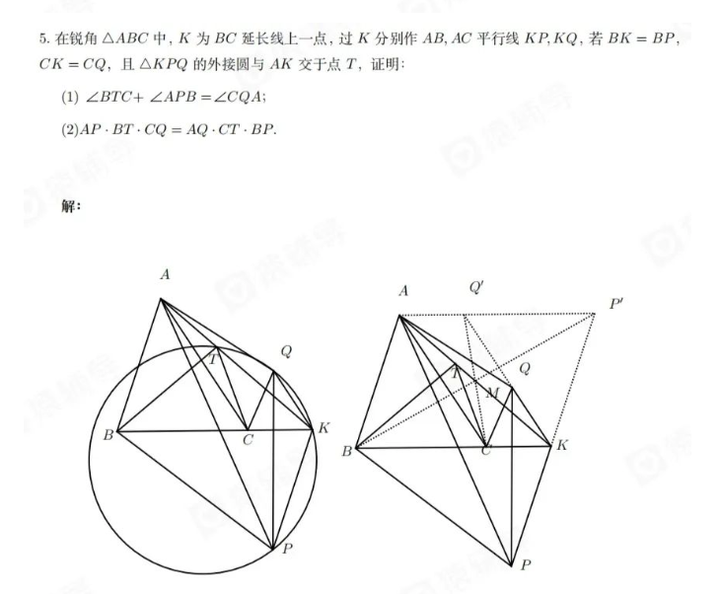
我们将其改写为alphageometry的输入，将原问题拆分为两个子问题，一个是 K,L,M,N 四点共圆，一个是 K，L，M，O

five_point_part1
f g h i j = pentagon f g h i j; a = intersection_ll a f j g h; b = intersection_ll b f g h i; c = intersection_ll c g h i j; d = intersection_ll d h i f j; e = intersection_ll e f g i j; o1 = circle o1 a f g; o2 = circle o2 b g h; o3 = circle o3 c h i; o4 = circle o4 d j i; o5 = circle o5 e j f; k = intersection_cc k o5 o1 f; l = intersection_cc l o1 o2 g; m = intersection_cc m o2 o3 h; n = intersection_cc n o3 o4 i; o = intersection_cc o o4 o5 j ? cyclic k l m n
five_point_part2
f g h i j = pentagon f g h i j; a = intersection_ll a f j g h; b = intersection_ll b f g h i; c = intersection_ll c g h i j; d = intersection_ll d h i f j; e = intersection_ll e f g i j; o1 = circle o1 a f g; o2 = circle o2 b g h; o3 = circle o3 c h i; o4 = circle o4 d j i; o5 = circle o5 e j f; k = intersection_cc k o5 o1 f; l = intersection_cc l o1 o2 g; m = intersection_cc m o2 o3 h; n = intersection_cc n o3 o4 i; o = intersection_cc o o4 o5 j ? cyclic k l m o

每个子问题大致花了三分钟，
第一部分的解：

==========================
 * From theorem premises:
A B C D E F G H I J K L M N O P Q R S : Points
C,B,F are collinear [00]
E,F,A are collinear [01]
C,B,H are collinear [02]
D,E,H are collinear [03]
D,I,C are collinear [04]
E,I,A are collinear [05]
D,J,E are collinear [06]
J,B,A are collinear [07]
KA = KB [08]
KF = KA [09]
LB = LC [10]
LG = LB [11]
MC = MD [12]
MH = MC [13]
NI = NE [14]
NE = ND [15]
OJ = OE [16]
OE = OA [17]
KA = KP [18]
OA = OP [19]
KB = KQ [20]
LB = LQ [21]
MC = MR [22]
LC = LR [23]
MD = MS [24]
ND = NS [25]

 * Auxiliary Constructions:
: Points


 * Proof steps:
001. KA = KB [08] & KF = KA [09] & KA = KP [18] ?  P,B,A,F are concyclic [26]
002. P,B,A,F are concyclic [26] & KA = KB [08] & KA = KP [18] & KB = KQ [20] ?  P,Q,B,F are concyclic [27]
003. P,Q,F,B are concyclic [27] ?  ∠PQB = ∠PFB [28]
004. MC = MR [22] & MC = MD [12] & MH = MC [13] & MD = MS [24] ?  D,C,S,H are concyclic [29]
005. D,C,S,H are concyclic [29] ?  ∠DSH = ∠DCH [30]
006. NI = NE [14] & NE = ND [15] & ND = NS [25] ?  D,I,S,E are concyclic [31]
007. D,I,S,E are concyclic [31] ?  ∠DSE = ∠DIE [32]
008. F,E,A are collinear [01] & C,B,H are collinear [02] & C,B,F are collinear [00] & ∠DSH = ∠DCH [30] & ∠DSE = ∠DIE [32] & D,I,C are collinear [04] & E,I,A are collinear [05] ?  ∠SEF = ∠SHF [33]
009. ∠SEF = ∠SHF [33] ?  H,S,E,F are concyclic [34]
010. OJ = OE [16] & OE = OA [17] & OA = OP [19] ?  E,P,J,A are concyclic [35]
011. E,P,J,A are concyclic [35] ?  ∠PEJ = ∠PAJ [36]
012. P,B,A,F are concyclic [26] ?  ∠PFB = ∠PAB [37]
013. C,B,H are collinear [02] & C,B,F are collinear [00] & D,E,H are collinear [03] & ∠PEJ = ∠PAJ [36] & D,J,E are collinear [06] & J,B,A are collinear [07] & ∠PFB = ∠PAB [37] ?  ∠PFH = ∠PEH [38]
014. ∠PFH = ∠PEH [38] ?  P,F,E,H are concyclic [39]
015. H,S,E,F are concyclic [34] & P,F,E,H are concyclic [39] ?  P,S,F,H are concyclic [40]
016. P,S,F,H are concyclic [40] ?  ∠PSH = ∠PFH [41]
017. ∠PQB = ∠PFB [28] & C,B,F are collinear [00] & ∠PSH = ∠PFH [41] & C,B,H are collinear [02] ?  ∠PSH = ∠PQB [42]
018. MC = MR [22] & MC = MD [12] & MH = MC [13] & MD = MS [24] & D,C,S,H are concyclic [29] ?  S,C,H,R are concyclic [43]
019. S,C,H,R are concyclic [43] ?  ∠SHC = ∠SRC [44]
020. LB = LQ [21] & LB = LC [10] & LG = LB [11] & LC = LR [23] ?  C,Q,R,B are concyclic [45]
021. C,Q,R,B are concyclic [45] ?  ∠RCB = ∠RQB [46]
022. ∠SHC = ∠SRC [44] & C,B,H are collinear [02] & ∠RCB = ∠RQB [46] ?  ∠RQB = ∠RSH [47]
023. ∠PSH = ∠PQB [42] & ∠RQB = ∠RSH [47] ?  ∠PSR = ∠PQR [48]
024. ∠PSR = ∠PQR [48] ?  Q,R,P,S are concyclic
==========================

第二部分的解：

==========================
 * From theorem premises:
A B C D E G H I J K L M N O P Q R T : Points
A,G,B are collinear [00]
C,G,D are collinear [01]
C,H,B are collinear [02]
E,H,D are collinear [03]
A,I,E are collinear [04]
C,I,D are collinear [05]
E,J,D are collinear [06]
A,J,B are collinear [07]
KA = KB [08]
LG = LB [09]
LB = LC [10]
MH = MC [11]
MC = MD [12]
NE = ND [13]
NI = NE [14]
OE = OA [15]
OJ = OE [16]
OA = OP [17]
KA = KP [18]
LB = LQ [19]
KB = KQ [20]
LC = LR [21]
MC = MR [22]
OE = OT [23]
NE = NT [24]

 * Auxiliary Constructions:
S : Points
ND = NS [25]

 * Proof steps:
001. LG = LB [09] & LB = LC [10] & LB = LQ [19] & LC = LR [21] ?  C,R,G,B are concyclic [26]
002. C,R,G,B are concyclic [26] ?  ∠CRG = ∠CBG [27]
003. MH = MC [11] & MC = MD [12] & MC = MR [22] ?  C,H,R,D are concyclic [28]
004. C,H,R,D are concyclic [28] ?  ∠CHD = ∠CRD [29]
005. E,J,D are collinear [06] & A,J,B are collinear [07] & A,G,B are collinear [00] & ∠CRG = ∠CBG [27] & ∠CHD = ∠CRD [29] & C,H,B are collinear [02] & E,H,D are collinear [03] ?  ∠RDJ = ∠RGJ [30]
006. ∠RDJ = ∠RGJ [30] ?  J,R,G,D are concyclic [31]
007. OA = OP [17] & OE = OA [15] & OE = OT [23] & OJ = OE [16] ?  A,E,J,T are concyclic [32]
008. A,E,J,T are concyclic [32] ?  ∠EAJ = ∠ETJ [33]
009. NE = ND [13] & ND = NS [25] & NE = NT [24] & NI = NE [14] ?  I,E,T,D are concyclic [34]
010. I,E,T,D are concyclic [34] ?  ∠EID = ∠ETD [35]
011. C,G,D are collinear [01] & A,J,B are collinear [07] & A,G,B are collinear [00] & ∠EAJ = ∠ETJ [33] & ∠EID = ∠ETD [35] & A,I,E are collinear [04] & C,I,D are collinear [05] ?  ∠GDT = ∠GJT [36]
012. ∠GDT = ∠GJT [36] ?  T,J,G,D are concyclic [37]
013. J,R,G,D are concyclic [31] & T,J,G,D are concyclic [37] ?  J,R,G,T are concyclic [38]
014. J,R,G,T are concyclic [38] ?  ∠JGR = ∠JTR [39]
015. OA = OP [17] & OE = OA [15] & OE = OT [23] & OJ = OE [16] ?  J,P,A,T are concyclic [40]
016. J,P,A,T are concyclic [40] ?  ∠JAP = ∠JTP [41]
017. ∠JGR = ∠JTR [39] & A,J,B are collinear [07] & A,G,B are collinear [00] & ∠JAP = ∠JTP [41] ?  ∠APT = ∠GRT [42]
018. LG = LB [09] & LB = LC [10] & LB = LQ [19] & LC = LR [21] & C,R,G,B are concyclic [26] ?  R,B,Q,G are concyclic [43]
019. R,B,Q,G are concyclic [43] ?  ∠RQB = ∠RGB [44]
020. KA = KP [18] & KA = KB [08] & KB = KQ [20] ?  A,Q,P,B are concyclic [45]
021. B,Q,P,A are concyclic [45] ?  ∠ABQ = ∠APQ [46]
022. ∠RQB = ∠RGB [44] & A,G,B are collinear [00] & ∠ABQ = ∠APQ [46] ?  ∠APQ = ∠GRQ [47]
023. ∠APT = ∠GRT [42] & ∠APQ = ∠GRQ [47] ?  ∠TPQ = ∠TRQ [48]
024. ∠TPQ = ∠TRQ [48] ?  P,Q,R,T are concyclic
==========================

注意到，作者提供的jgex_ag_231.txt数据集里，与我们的略有不同，也有另外一个五点共圆命题的构造方案：

examples/complete2/000/complete_004_6_GDD_FULL_81-109_106.gex
q4 q1 q3 q0 q2 = pentagon q4 q1 q3 q0 q2; p0 = on_line p0 q4 q1, on_line p0 q0 q2; p4 = on_line p4 q4 q1, on_line p4 q3 q0; p3 = on_line p3 q3 q0, on_line p3 q4 q2; p2 = on_line p2 q1 q3, on_line p2 q4 q2; p1 = on_line p1 q1 q3, on_line p1 q0 q2; o0 = circle o0 q0 p0 p4; o1 = circle o1 p1 q1 p0; o4 = circle o4 p4 p3 q4; o3 = circle o3 p3 p2 q3; o2 = circle o2 p1 p2 q2; m0 = on_circle m0 o0 q0, on_circle m0 o1 q1; m4 = on_circle m4 o0 q0, on_circle m4 o4 q4; m3 = on_circle m3 o4 q4, on_circle m3 o3 q3; m2 = on_circle m2 o3 q3, on_circle m2 o2 q2; m1 = on_circle m1 o2 q2, on_circle m1 o1 q1 ? cyclic m4 m3 m2 m1

对于这个输入，alphageometry也是能够给出解的：

==========================
 * From theorem premises:
A B C D E F G H I J K L M N O Q R S T : Points
B,A,F are collinear [00]
D,E,F are collinear [01]
D,C,G are collinear [02]
B,G,A are collinear [03]
D,C,H are collinear [04]
H,A,E are collinear [05]
I,A,E are collinear [06]
C,I,B are collinear [07]
D,J,E are collinear [08]
C,B,J are collinear [09]
KD = KF [10]
KF = KG [11]
LJ = LB [12]
LB = LF [13]
MH = MA [14]
MG = MH [15]
NI = NC [16]
NH = NI [17]
OJ = OI [18]
OI = OE [19]
KQ = KD [20]
MQ = MA [21]
MR = MA [22]
NR = NC [23]
NS = NC [24]
OS = OE [25]
LT = LB [26]
OT = OE [27]

 * Auxiliary Constructions:
P : Points
KP = KD [28]
LP = LB [29]

 * Proof steps:
001. KF = KG [11] & KD = KF [10] & KP = KD [28] ?  D,P,G,F are concyclic [30]
002. KP = KD [28] & KQ = KD [20] & KD = KF [10] & D,P,G,F are concyclic [30] ?  P,G,D,Q are concyclic [31]
003. KP = KD [28] & KQ = KD [20] & KD = KF [10] & D,P,G,F are concyclic [30] ?  P,G,F,Q are concyclic [32]
004. P,G,D,Q are concyclic [31] ?  ∠PDG = ∠PQG [33]
005. MH = MA [14] & MR = MA [22] & MG = MH [15] ?  H,R,G,A are concyclic [34]
006. MH = MA [14] & MQ = MA [21] & MG = MH [15] & H,R,G,A are concyclic [34] ?  R,H,G,Q are concyclic [35]
007. G,R,Q,H are concyclic [35] ?  ∠GQR = ∠GHR [36]
008. ∠PDG = ∠PQG [33] & D,C,G are collinear [02] & ∠GQR = ∠GHR [36] & D,C,H are collinear [04] ?  ∠HRQ = ∠DPQ [37]
009. NI = NC [16] & NR = NC [23] & NH = NI [17] ?  R,C,I,H are concyclic [38]
010. NI = NC [16] & NS = NC [24] & NR = NC [23] & R,C,I,H are concyclic [38] ?  C,I,H,S are concyclic [39]
011. NI = NC [16] & NS = NC [24] & NR = NC [23] & R,C,I,H are concyclic [38] ?  S,C,R,H are concyclic [40]
012. S,C,R,H are concyclic [40] ?  ∠SCH = ∠SRH [41]
013. C,I,H,S are concyclic [39] ?  ∠SCH = ∠SIH [42]
014. OJ = OI [18] & OI = OE [19] & OS = OE [25] ?  J,I,E,S are concyclic [43]
015. J,I,E,S are concyclic [43] ?  ∠EIS = ∠EJS [44]
016. D,E,J are collinear [08] & ∠SCH = ∠SIH [42] & D,C,H are collinear [04] & I,A,E are collinear [06] & H,A,E are collinear [05] & ∠EIS = ∠EJS [44] ?  ∠SJD = ∠SCD [45]
017. ∠SJD = ∠SCD [45] ?  D,C,J,S are concyclic [46]
018. D,P,G,F are concyclic [30] ?  ∠PFG = ∠PDG [47]
019. LJ = LB [12] & LP = LB [29] & LB = LF [13] ?  P,B,J,F are concyclic [48]
020. P,B,J,F are concyclic [48] ?  ∠BFP = ∠BJP [49]
021. C,B,J are collinear [09] & ∠PFG = ∠PDG [47] & B,G,A are collinear [03] & B,A,F are collinear [00] & D,C,G are collinear [02] & ∠BFP = ∠BJP [49] ?  ∠PJC = ∠PDC [50]
022. ∠PJC = ∠PDC [50] ?  D,C,J,P are concyclic [51]
023. D,C,J,S are concyclic [46] & D,C,J,P are concyclic [51] ?  S,P,C,D are concyclic [52]
024. S,P,C,D are concyclic [52] ?  ∠DPS = ∠DCS [53]
025. ∠SCH = ∠SRH [41] & D,C,H are collinear [04] & ∠DPS = ∠DCS [53] ?  ∠DPS = ∠HRS [54]
026. ∠HRQ = ∠DPQ [37] & ∠DPS = ∠HRS [54] ?  ∠PQR = ∠PSR [55]
027. ∠PQR = ∠PSR [55] ?  P,R,Q,S are concyclic [56]
028. P,G,F,Q are concyclic [32] ?  ∠PFG = ∠PQG [57]
029. R,H,G,A are concyclic [34] & R,H,G,Q are concyclic [35] ?  G,A,R,Q are concyclic [58]
030. G,A,R,Q are concyclic [58] ?  ∠GAR = ∠GQR [59]
031. ∠PFG = ∠PQG [57] & B,G,A are collinear [03] & B,A,F are collinear [00] & ∠GAR = ∠GQR [59] ?  ∠ARQ = ∠FPQ [60]
032. LJ = LB [12] & LT = LB [26] & LB = LF [13] ?  T,B,J,F are concyclic [61]
033. T,B,J,F are concyclic [61] & P,B,J,F are concyclic [48] ?  F,P,T,J are concyclic [62]
034. F,P,T,J are concyclic [62] ?  ∠FPT = ∠FJT [63]
035. D,E,J are collinear [08] & ∠FPT = ∠FJT [63] & D,E,F are collinear [01] ?  ∠PTJ = ∠(PF-DJ) [64]
036. OS = OE [25] & OT = OE [27] & OI = OE [19] & J,I,E,S are concyclic [43] ?  T,J,I,E are concyclic [65]
037. T,J,I,E are concyclic [65] ?  ∠EIT = ∠EJT [66]
038. D,E,J are collinear [08] & I,A,E are collinear [06] & H,A,E are collinear [05] & ∠EIT = ∠EJT [66] ?  ∠JTI = ∠(DJ-HI) [67]
039. ∠PTJ = ∠(PF-DJ) [64] & ∠JTI = ∠(DJ-HI) [67] ?  ∠(PF-HI) = ∠PTI [68]
040. T,B,J,F are concyclic [61] ?  ∠BFJ = ∠BTJ [69]
041. I,A,E are collinear [06] & ∠BFJ = ∠BTJ [69] & B,A,F are collinear [00] & D,E,J are collinear [08] & D,E,F are collinear [01] & ∠EIT = ∠EJT [66] ?  ∠AIT = ∠ABT [70]
042. ∠AIT = ∠ABT [70] ?  T,B,I,A are concyclic [71]
043. H,R,G,A are concyclic [34] ?  ∠GAR = ∠GHR [72]
044. R,C,I,H are concyclic [38] ?  ∠CIR = ∠CHR [73]
045. C,I,B are collinear [07] & ∠GAR = ∠GHR [72] & B,G,A are collinear [03] & D,C,H are collinear [04] & D,C,G are collinear [02] & ∠CIR = ∠CHR [73] ?  ∠BIR = ∠BAR [74]
046. ∠BIR = ∠BAR [74] ?  R,B,I,A are concyclic [75]
047. T,B,I,A are concyclic [71] & R,B,I,A are concyclic [75] ?  R,I,A,T are concyclic [76]
048. A,I,R,T are concyclic [76] ?  ∠AIT = ∠ART [77]
049. ∠(PF-HI) = ∠PTI [68] & I,A,E are collinear [06] & H,A,E are collinear [05] & ∠AIT = ∠ART [77] ?  ∠ART = ∠FPT [78]
050. ∠ARQ = ∠FPQ [60] & ∠ART = ∠FPT [78] ?  ∠RQP = ∠RTP [79]
051. ∠RQP = ∠RTP [79] ?  P,T,R,Q are concyclic [80]
052. P,R,Q,S are concyclic [56] & P,T,R,Q are concyclic [80] ?  Q,R,S,T are concyclic
==========================

补充说明；
我们在运行的过程中也遇到了一个之前有人遇到的bug，numericals.py出了bug，修复方式见https://github.com/google-deepmind/alphageometry/issues/20
CMO2023
正如作者说的，他们的几何命题形式化方案，能大概形式化75%的imo命题。有25%的他们的方案不太能形式化。
比如下面的这道CMO2023年的几何题，牵扯到角的和，与多个边的乘积，我想了半天也没有想出来能否用作者的规则将其转化为alphageometry的输入。


大家可以看这个解析，来看原问题如何解决。2023年第三十九届CMO试题及解析
我已经在github上提了相关的issuehttps://github.com/google-deepmind/alphageometry/issues/35#issue-2092501017，
蹲一个最新进展吧。。。
似乎还是以符号为主深度学习为辅，总之先占个坑看完再写
单论解决几何问题，确实是一种巧妙的方法，某种意义上其实和AlphaGo很像：符号引擎负责机械的推理，神经网络负责剪枝。只不过，这里剪枝的范围更大，可以说是有无限种分支
但是，正如作者自己承认的，AlphaGeometry想要推广到其它更复杂的领域，是极其困难的，至少需要满足4个条件：
An implementation of the domain’s objects and definitions.A random premise sampler.The symbolic engine(s) that operate within the implementation (1).A traceback procedure for the symbolic engine.
总结一下，这四个条件意味着在该领域必须可以建立一个符号逻辑引擎。然而，不用说现实世界，就算是中学考试题，建立这样的引擎也是极度困难的吧？就算能够建立，用户使用时将自然语言描述的问题转写为形式化语言也是一件麻烦事（当然这一步可以借助LLM），毕竟不是每个领域是都如同几何这样严格公理化的
总体来说，我会期待这类方法用于纯数学研究中的定理证明，但对在更日常的场景中的应用不抱希望。目前为止，人类的工具中，能应对真正广阔领域的task的仍然只有LLM
评论区提醒算不上无限种分支，因为构造的辅助线实际上仅限于生成器的几种动作。这样来看就更简化了
没有必要批评transformer的数据利用率低，“人类可不需要做过数百万道几何题才能学会”——人类的学习更接近prompt而非这篇文章的train from scratch。人类的预训练数据，则是从出生开始7*24的视觉听觉嗅觉触觉味觉，无论是质量还是数量，任何LLM的数据集都比不上
至于prompt的数据效率，这篇文章里GPT-4可是在prompt learning的情况下配合符号推理答对了15题，已经超过大多数人类了吧？没几个人敢说见过几个例子就能挑战奥赛题。prompt learning的数据效率并不差，真正的问题在于上限低
DeepMind真是nature的常客了。
对于agent，LLMs到底有什么用？读Deepmind论文FunSearch和AlphaGeometry有感
论文标题是Solving olympiad geometry without human demonstrations，但不易过度解读synthetic data在其它问题中的作用，因为这里需要很多条件才能工作。
AlphaGeometry的方法，基本限于欧几里得几何，暂时还不能拓展到数学，更不能拓展到AGI
[收藏本文] 【下载本文】
   自然科学 最新文章
海南一村民被眼镜王蛇咬死，多名消防员和村
有哪些不起眼的牢底坐穿兽？
美国耕地面积比中国大，可为什么粮食产量不
如何看待同济大学2024国家科技三大奖颗粒无
假如航母被蓝鲸全速前进撞一下会怎么样？
你见过最狠的SCI评论是什么?
你在实验室最惊险的瞬间是什么？
牛顿生活在中国，会有什么成就？
虎鲸为什么不吃人？
数学为什么这么可笑？
上一篇文章      下一篇文章      查看所有文章
加:2024-01-22 14:51:28  更:2024-01-22 14:53:24 
 
 
股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事
网站联系: qq:121756557 email:121756557@qq.com  天天财汇