| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 1992??和2001??哪个更大? -> 正文阅读 |
|
|
[时尚穿搭]1992??和2001??哪个更大? |
| [收藏本文] 【下载本文】 |
|
男朋友给我出的数学题,不让计算器。当年身为高中课代表的我,大学不学数学,现在看到数学题脑阔晕,可以ball ball各位小伙伴帮忙吗?阿里嘎多! |
|
没想到数学还能有上热搜的时候,之前我一直以为明星打喷嚏比较重要(doge) 199200与200199" role="presentation">与199200与200199{199^{200}与200^{199}} 同取对数后: 200ln⁡199与199ln⁡200" role="presentation">与200ln?199与199ln?200200\ln199与199\ln 200 同除以 199⋅200" role="presentation">199?200199\cdot200 : ln⁡199199与ln⁡200200" role="presentation">与ln?199199与ln?200200\frac{\ln 199}{199}与\frac{\ln 200}{200} 于是构造函数 f(x)=ln⁡xx" role="presentation">=f(x)=ln?xxf(x)=\frac{\ln x}{x} 利用单调性比大小 f′(x)=limΔx→0ln⁡(x+Δx)x+Δx−ln⁡xxΔx=limΔx→0xln⁡(1+Δxx)−Δxln⁡xxΔx(x+Δx)=limΔx→0Δx−Δxln⁡xxΔx(x+Δx)=1−ln⁡xx2" role="presentation">====f′(x)=limΔx→0ln?(x+Δx)x+Δx?ln?xxΔx=limΔx→0xln?(1+Δxx)?Δxln?xxΔx(x+Δx)=limΔx→0Δx?Δxln?xxΔx(x+Δx)=1?ln?xx2\begin{align} f'(x)=&\lim_{\Delta x\to0}\frac{\frac{\ln (x+\Delta x)} {x+\Delta x}-\frac{\ln x}{x}}{\Delta x}\\=&\lim_{\Delta x\to0}\frac{x\ln(1+\frac{\Delta x}{x})-\Delta x\ln x}{x\Delta x(x+\Delta x)}\\=&\lim_{\Delta x\to0}\frac{\Delta x-\Delta x\ln x}{x\Delta x(x+\Delta x)}\\=&\frac{1-\ln x}{x^2} \end{align} 199,200∈(e,+∞)减区间" role="presentation">减区间199,200∈(e,+∞)减区间199,200\in(e,+∞)减区间 因此: ln⁡199199>ln⁡200200199200>200199" role="presentation">>>ln?199199>ln?200200199200>200199\begin{align} \frac{\ln 199}{199}>\frac{\ln 200}{200} \\{199^{200}>200^{199}} \end{align} |
|
高赞怎么都是硬算的,我来个导数证明吧。 |

|
|
|
|
先说结论, 200^{199}">199200>200199" role="presentation">199200>200199199^{200}>200^{199} ,而且类似的情况 9999^{9998}">99989999>99999998" role="presentation">99989999>999999989998^{9999}>9999^{9998} 也同样成立 已知 e<a<b" role="presentation">e<a<ba^b>b^a 。 证明: b^a">ab>ba" role="presentation">ab>baa^b>b^a 等价于 e^{a*lnb}">eb∗lna>ea∗lnb" role="presentation">eb?lna>ea?lnbe^{b*lna}>e^{a*lnb},即 a*lnb">b∗lna>a∗lnb" role="presentation">b?lna>a?lnbb*lna > a*lnb 只需证明 a*lnb">b∗lna>a∗lnb" role="presentation">b?lna>a?lnbb*lna > a*lnb 即说明 b^a">ab>ba" role="presentation">ab>baa^b>b^a 。 令 f(x)=xlna−alnx" role="presentation">f(x)=xlna?alnxf(x)=xlna-alnx ,得 f(a)=0" role="presentation">f(a)=0f(a)=0 f′(x)=lna−ax" role="presentation">f′(x)=lna?axf'(x)=lna-\frac{a}{x} ,当 a<x<b" role="presentation">a<x<bf'(x)>0 , 故 f(x)" role="presentation">f(x)f(x) 在 [a,b]" role="presentation">[a,b][a,b] 上单调递增 由题得 a">b>a" role="presentation">b>ab>a ,故 f(a)=0">f(b)>f(a)=0" role="presentation">f(b)>f(a)=0f(b)>f(a)=0 ,即 0">f(b)>0" role="presentation">f(b)>0f(b)>0 所以 0">blna−alnb>0" role="presentation">blna?alnb>0blna-alnb>0 ,也就是 b^a">ab>ba" role="presentation">ab>baa^b>b^a 将a=199,b=200代入,可知 200^{199}">199200>200199" role="presentation">199200>200199199^{200}>200^{199} ,所以不管a,b取多少,只要满足大于e,就算是 500^{400}">400500>500400" role="presentation">400500>500400400^{500}>500^{400} 或者 9999^{9998}">99989999>99999998" role="presentation">99989999>999999989998^{9999}>9999^{9998} 也同样成立。 |
|
先说是什么 199²⁰⁰>200¹⁹⁹" role="presentation">2??>1??1992??>2001??1992??>2001?? 再问为什么 我就写初中同学也看得懂的解法吧 200¹⁹⁹199²⁰⁰" role="presentation">1??2??2001??1992??\frac{2001??}{1992??} 两数相除 如果>1则2001??大,<1则1992??大,=1则一样大 ∵ 200¹⁹⁹199²⁰⁰=200¹⁹⁹199¹⁹⁹×199=(200199)¹⁹⁹×1199" role="presentation">1??2??=1??1??=1??2001??1992??=2001??1991??×199=(200199)1??×1199\frac{2001??}{1992??}=\frac{2001??}{1991??×199}=\left( \frac{200}{199}\right)1??×\frac{1}{199} =(1+1199)¹⁹⁹×1199" role="presentation">=1??=(1+1199)1??×1199=\left( 1+\frac{1}{199} \right)1??×\frac{1}{199} <(1+12)(1+13)(1+14)....×(1+1199)×(1+1199)×1199" role="presentation"><<(1+12)(1+13)(1+14)....×(1+1199)×(1+1199)×1199<\left( 1+\frac{1}{2} \right)\left( 1+\frac{1}{3} \right)\left( 1+\frac{1}{4} \right)....×\left( 1+\frac{1}{199} \right)×\left( 1+\frac{1}{199} \right)× \frac{1}{199} 合并 =32×43×54....×200199×200199×1199" role="presentation">==32×43×54....×200199×200199×1199=\frac{3}{2}×\frac{4}{3}×\frac{5}{4}....×\frac{200}{199}×\frac{200}{199}×\frac{1}{199} 约分 =2002×200199×1199" role="presentation">==2002×200199×1199=\frac{200}{2}×\frac{200}{199}×\frac{1}{199} =20000199²" role="presentation">=2=200001992=\frac{20000}{1992} 又∵ 20000199²<1" role="presentation">2<200001992<1\frac{20000}{1992}<1 ∴ 199²⁰⁰>200¹⁹⁹" role="presentation">2??>1??1992??>2001??1992??>2001?? 其实呢 这种题一般只会出现在填空题 我们只要记住一条公式就行:在 n≥e的条件下,nⁿ⁺¹>(n+1)ⁿ" role="presentation">的条件下,??1>()?n≥e的条件下,n??1>(n+1)?n≥e的条件下,n??1>(n+1)? 释:e为自然对底数,是一个无限不循环小数,其值约等于2.718281828459… 祝大家牛年快乐 |

|
|
|
|
鉴于评论中有大量的回答是:取对数,构造函数。有必要先声明 取对数构造函数再求导的方法是最基本也是最容易想到的方法,就好比用方程解应用题一样。已经有很多答案详实地、不知疲倦地展示了这种方法,我就不再浪费时间于此了。我用均值不等式来做完全是因为看到答案里面没人用,而均值不等式又属于非常基础的但有一定技巧的方法,而且觉得用均值不等式最省墨,并不是说这种方法要比构造函数的方法好,更不是说我不会用其他方法。。。(8.2补) ------------------------------------------------------------------------------------------- 看了琳琅满目的回答,有用高等数学方法的,有用初中比商法放缩的,有用不完全归纳当填空题做的,还有各种抖机灵反智用数值计算侮辱数学的,真可谓百般红紫斗芳菲,叫人应接不暇!可翻看了这么多,居然没有用均值不等式的!怎么可以没有均值不等式?!于是我琢磨了一下 200199200=200198⋅100⋅2200<198×200+100+2200<199×200200=199" role="presentation">200199200=200198?100?2200<198×200+100+2200<199×200200=199\frac{a_{1}+a_{2}+a_{3}+......+a_{n}}{n}\geq\sqrt[n]{a_{1}a_{2}a_{3}......a_{n}} ,算术平均值大于等于几何平均值, a1=a2=a3=......=an" role="presentation">a1=a2=a3=......=ana_{1}=a_{2}=a_{3}=......=a_{n} 时等号成立 ====================【7.24更】===================== 感觉得加点东西才对得起大家的赞和回复,那我推广到一般情况吧 比较(n+1)n" role="presentation">(n+1)n(n+1)^{n} 和 nn+1" role="presentation">nn+1n^{n+1} 的大小,其中 n∈N" role="presentation">n∈Nn\in N (n+1)nn+1=(n+1)n−1n+1n+1n+1<(n−1)(n+1)+2n+1n+1=n−1+2n+1" role="presentation">(n+1)nn+1=(n+1)n?1n+1n+1n+1<(n?1)(n+1)+2n+1n+1=n?1+2n+1n-1+\frac{2}{\sqrt{n+1}}\leq n ,就能得到 (n+1)nn+1<n⇒(n+1)n<nn+1" role="presentation">(n+1)nn+1<n?(n+1)n<nn+1n-1+\frac{2}{\sqrt{n+1}}\leq n 得到 n≥3" role="presentation">n≥3n\geq3 从而证明了当 n≥3" role="presentation">n≥3n\geq3 时, (n+1)n<nn+1" role="presentation">(n+1)n<nn+1n=0,1,2 的情况,带入进去计算就能得到 n^{n+1}">(n+1)n>nn+1" role="presentation">(n+1)n>nn+1(n+1)^{n}>n^{n+1} ------------------------------------------------------------------------------- 感觉这就是初等的方法里能走得最远的结果。 其实构造 f(x)=lnxx" role="presentation">f(x)=lnxxf(x)=\frac{lnx}{x} 才是可推广的标准化方法,能得到最强的结果,而且会对这个问题有更深入的理解。均值不等式技巧性强,属于抖机灵的解法。 ============下面再附赠一个初中水平的奇技淫巧的方法吧============== 要比较 200199" role="presentation">200199200^{199}和199200" role="presentation">199200199^{200} ,就是要比较 200199199×200" role="presentation">200199199×200200^{\frac{199}{199\times200}} 和 199200199×200" role="presentation">199200199×200199^{\frac{200}{199\times200}} ,那就是比较 200200" role="presentation">200200\sqrt[200]{200} 和 199199" role="presentation">199199\sqrt[199]{199} 200=199×200199" role="presentation">200=199×200199200=199\times\frac{200}{199} =(199199)199×200199=(200200)199×200200⋅⋅⋅⋅⋅⋅(1)" role="presentation">=(199199)199×200199=(200200)199×200200??????(1)\qquad =\left( \sqrt[199]{199}\right)^{199} \times\frac{200}{199}=\left( \sqrt[200]{200} \right)^{199} \times \sqrt[200]{200} \qquad \cdot\cdot\cdot\cdot\cdot\cdot\quad(1) 如果能比较 200200" role="presentation">200200\sqrt[200]{200} 和 200199" role="presentation">200199\frac{200}{199} 的大小,就能比较 200200" role="presentation">200200\sqrt[200]{200} 和 199199" role="presentation">199199\sqrt[199]{199} 的大小 \left( \frac{200}{199}\right)^{200}">200=21×32×43……×200199⏟共199项=2×2×32×43……×200199⏟共200项>(200199)200" role="presentation">共项共项200=21×32×43……×200199?共199项=2×2×32×43……×200199?共200项>(200199)200200 =\underbrace{\frac{2}{1}\times\frac{3}{2}\times\frac{4}{3}……\times\frac{200}{199}}_{共199项}=\underbrace{\sqrt{2}\times\sqrt{2}\times\frac{3}{2}\times\frac{4}{3}……\times\frac{200}{199}}_{共200项}>\left( \frac{200}{199}\right)^{200} 所以 \frac{200}{199}">200200>200199" role="presentation">200200>200199\sqrt[200]{200}>\frac{200}{199},由 (1)" role="presentation">(1)(1) 式 立马得到 200200<199199" role="presentation">200200<199199\sqrt[n+1]{n+1} 和 nn" role="presentation">nn\sqrt[n]{n} 要让 \left( \frac{n+1}{n}\right)^{n+1}">2×2×32×43……×n+1n⏟共n+1项>(n+1n)n+1" role="presentation">共项2×2×32×43……×n+1n?共n+1项>(n+1n)n+1\underbrace{\sqrt{2}\times\sqrt{2}\times\frac{3}{2}\times\frac{4}{3}……\times\frac{n+1}{n}}_{共n+1项}>\left( \frac{n+1}{n}\right)^{n+1} 成立,必须 \frac{n+1}{n}">2>n+1n" role="presentation">2>n+1n\sqrt{2}>\frac{n+1}{n} 所以 \sqrt{2}+1">n>2+1" role="presentation">n>2+1n>\sqrt{2}+1 ,也就是 n≥3" role="presentation">n≥3n\geq 3 水平越来越低了,就一初中竞赛水平,当然是不能和高等数学的方法比的。。。。 容我再想想有没有小学的方法 |
|
记住下面这条定律,以后碰到任何此类问题,别说199,即便问1亿,皆可1秒钟作答: 在正整数范围内(除1和2外),任何底-指数互换的数值比较,都始终遵循“指数大则值大”的规律! 看了很多专业的回答,令人钦佩! 本人高数已忘了,现在也不是数学的专业人士,因此只能以一种粗放直观的方式,抛砖引玉。 关于1992??和2001??谁大,其实不就是看两者相除是否大于1嘛。 首先,从1,2开始,简单罗列数据,不就一目了然了吗?底指只差1的数字,互换比较,除了1和2不够争气以外,其余任何正整数,一律统统都是指数大,数值越大。而且是随着数据的增大,差距也越来越大。这基本就可以确定本题的答案。 |

|
|
如果将上述倍数计算方法转换成公式,那么可以通过被除数和除数同时除以(x^x,x对应的是题中的199), 得到比值公式: |
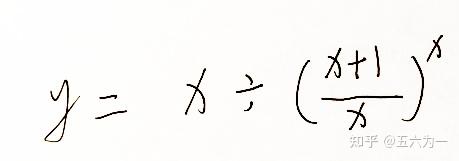
|
|
此公式,只要x大于2,y永远大于1。 利用这公式来算,那就非常简单了,别说199,就是199999999999^200000000000和200000000000^199999999999谁大,都能轻松用你的计算器算出来。 当x=1时,y为0.5; 当x=2时,y为0.889; 当x=5时,y为2.0094; 当x=199时,y为73.3916(就是说,1992??比2001??大73.3916倍); 当x=19999999999时,y为7357588214.8432; 当x=19999999999999999999时,y为2e+19; .......... 总之,除了1和2外,其余任何正整数底幂互转比较,一律统统都是指数大,数值越大,而且随着x变大,差距也越来越大。 日后碰到此类问题,就不用过多想了,指数大值大。 |
|
考虑函数 f(x)=\frac{\ln x}{x}, 求导易知 f(x) 在 (0,e) 上递增, 在 (e,+\infty) 上递减, 所以 f(200)=\frac{\ln200}{200}.">\frac{\ln199}{199}=f(199)>f(200)=\frac{\ln200}{200}. 于是 199\ln200,">200\ln199>199\ln200, 所以 200^{199}.">199^{200}>200^{199}. |
|
不难发现 199^200=5896784843701866315830202306247774762972638982405042480372238189012365044783448228280875028875684277127088378956152713197320945688565673304729984010537727226637040943165593052367979000124463424161858464934947067680269075228341562695042312463815883441507512003942871781958205145461989665812045325106145074842960481661294209203262577314061569045152694421556602495323466256365196176516277494056642637786305854049111948156579863012416891273717889898672613595960001 而200^199=80346902212949513777098104617058130126110149689139641765068800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 通过观察位数可得199^200>200^199 多说不如多做,一些简单的乘法题可以动笔算一算,自然就能找到答案 评论区有人说笔算这个有点困难,但实际上,我们都是用FFT心算的 我都惊了,这条回答一夜之间加了800赞,还有这么多人评论 2022 10.7 upd:1w赞啦!!111 |
|
这是吉米多维奇的0010.1.б题。这道题在俄文原版书上有,但是国内很多翻译版本删去了这道题。 |

|
|
在 n\geq3 的条件下,有 (n+1)^n">n^{n+1}>(n+1)^n --------- 证明方法一: 如果不局限于数学归纳法,可以这样证明: 根据自然常数的极限 n+2+1/n>n+2 1+1/(n+1)">1+1/n>1+1/(n+1) 不等式相乘,所以 (n+2)(1+1/(n+1))^n">(n+2+1/n)(1+1/n)^n>(n+2)(1+1/(n+1))^n 上面化简为 (n+2)^{n+1}/(n+1)^n">(n+1)^{n+2}/n^{n+1}>(n+2)^{n+1}/(n+1)^n 如果n成立,则 (n+1)^n">n^{n+1}>(n+1)^n 不等式相乘,所以 (n+2)^{n+1}">(n+1)^{n+2}>(n+2)^{n+1} 上面的推导说明了:如果n成立那么n+1成立。由数学归纳法,证明了不等式成立。 |
|
大家给的方法都太难了,我一个八岁的小朋友完全看不懂呜呜 数学,还是需要回归原点,感受最淳朴的方法 200^{199} = 80346902212949513777098104617058130126110149689139641765068800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 199^{200} = 5896784843701866315830202306247774762972638982405042480372238189012365044783448228280875028875684277127088378956152713197320945688565673304729984010537727226637040943165593052367979000124463424161858464934947067680269075228341562695042312463815883441507512003942871781958205145461989665812045325106145074842960481661294209203262577314061569045152694421556602495323466256365196176516277494056642637786305854049111948156579863012416891273717889898672613595960001 由上易知 200^{199}-199^{200}= -5816437941488916802053104201630716632846528832715902838607169389012365044783448228280875028875684277127088378956152713197320945688565673304729984010537727226637040943165593052367979000124463424161858464934947067680269075228341562695042312463815883441507512003942871781958205145461989665812045325106145074842960481661294209203262577314061569045152694421556602495323466256365196176516277494056642637786305854049111948156579863012416891273717889898672613595960001 不难发现数 -5816437941488916802053104201630716632846528832715902838607169389012365044783448228280875028875684277127088378956152713197320945688565673304729984010537727226637040943165593052367979000124463424161858464934947067680269075228341562695042312463815883441507512003942871781958205145461989665812045325106145074842960481661294209203262577314061569045152694421556602495323466256365196176516277494056642637786305854049111948156579863012416891273717889898672613595960001 小于零 所以 200^{199}200^{199}<199^{200} [1] 参考^本回答感谢Visual Studio Code和Python的支持,Python可以进行高位精确的大数运算 |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |