| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 数学史上你认为最丑陋的公式是什么? -> 正文阅读 |
|
|
[时尚穿搭]数学史上你认为最丑陋的公式是什么? |
| [收藏本文] 【下载本文】 |
|
姊妹篇: 数学史上你认为最美的公式是什么? |
|
波尔文积分(Borwein integral) 此特殊积分由波尔文父子(David Borwein & Jonathan Borwein)于 2001 年首次提出,用于举例说明【看似成立的数学规律会在某个时刻突然失效】。 这是一个涉及 sinc 函数的积分,常见的例子为: ∫0∞sin⁡(x)xdx=π2" role="presentation">∫0∞sin?(x)xdx=π2\int_{0}^{\infty}\frac{\sin(x)}{x}\mathrm{d}x=\frac{\pi}{2} ∫0∞sin⁡(x)xsin⁡(x/3)x/3dx=π2" role="presentation">∫0∞sin?(x)xsin?(x/3)x/3dx=π2\int_{0}^{\infty}\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\mathrm{d}x=\frac{\pi}{2} ∫0∞sin⁡(x)xsin⁡(x/3)x/3sin⁡(x/5)x/5dx=π2" role="presentation">∫0∞sin?(x)xsin?(x/3)x/3sin?(x/5)x/5dx=π2\int_{0}^{\infty}\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\frac{\sin(x/5)}{x/5}\mathrm{d}x=\frac{\pi}{2} ∫0∞sin⁡(x)xsin⁡(x/3)x/3sin⁡(x/5)x/5sin⁡(x/7)x/7dx=π2" role="presentation">∫0∞sin?(x)xsin?(x/3)x/3sin?(x/5)x/5sin?(x/7)x/7dx=π2\int_{0}^{\infty}\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\frac{\sin(x/5)}{x/5}\frac{\sin(x/7)}{x/7}\mathrm{d}x=\frac{\pi}{2} 此规律一直到: ∫0∞sin⁡(x)xsin⁡(x/3)x/3...sin⁡(x/13)x/13dx=π2" role="presentation">∫0∞sin?(x)xsin?(x/3)x/3...sin?(x/13)x/13dx=π2\int_{0}^{\infty}\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}...\frac{\sin(x/13)}{x/13}\mathrm{d}x=\frac{\pi}{2} 依然成立。 好了,算到这里你是不是会想:哦,多棒的规律啊!然后得意洋洋地开始测试下一个数。 然而,打脸来得就是这么猝不及防: ∫0∞sin⁡(x)xsin⁡(x/3)x/3...sin⁡(x/15)x/15dx=467807924713440738696537864469935615849440640907310521750000π" role="presentation">∫0∞sin?(x)xsin?(x/3)x/3...sin?(x/15)x/15dx=467807924713440738696537864469935615849440640907310521750000π\int_{0}^{\infty}\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}...\frac{\sin(x/15)}{x/15}\mathrm{d}x=\frac{467807924713440738696537864469}{935615849440640907310521750000}\pi =π2−6879714958723010531935615849440640907310521750000π" role="presentation">=π2?6879714958723010531935615849440640907310521750000π=\frac{\pi}{2}-\frac{6879714958723010531}{935615849440640907310521750000}\pi 烂,烂尾了…… 令人头大。 凭着直觉,你可能以为规律是这样的: ∫0∞∏k=0nsin⁡(akx)akxdx=π2,ak=12k+1" role="presentation">∫0∞∏k=0nsin?(akx)akxdx=π2,ak=12k+1\int _{0}^{\infty }\prod _{k=0}^{n}{\frac {\sin(a_{k}x)}{a_{k}x}}\,\mathrm{d}x=\frac{\pi}{2}, a_{k}=\frac{1}{2k+1} 简洁而美丽。 实际上它的通式却是这样的: ∫0∞∏k=0nsin⁡(akx)akxdx=π2a0·12nn!∏k=1nak∑γ∈{±1}nεγbγnsgn⁡(bγ),ak=12k+1," role="presentation">,∫0∞∏k=0nsin?(akx)akxdx=π2a0·12nn!∏k=1nak∑γ∈{±1}nεγbγnsgn?(bγ),ak=12k+1,\int _{0}^{\infty }\prod _{k=0}^{n}{\frac {\sin(a_{k}x)}{a_{k}x}}\,\mathrm{d}x=\frac{\pi}{2a_{0}}·{\frac {1}{2^{n}n!\prod _{k=1}^{n}a_{k}}}\sum _{\gamma \in \{\pm 1\}^{n}}\varepsilon _{\gamma }b_{\gamma }^{n}\operatorname {sgn}(b_{\gamma }), a_{k}=\frac{1}{2k+1}, γ=(γ1,γ2,…,γn)∈{±1}n,bγ=a0+γ1a1+γ2a2+⋯+γnan,εγ=γ1γ2⋯γn" role="presentation">γ=(γ1,γ2,…,γn)∈{±1}n,bγ=a0+γ1a1+γ2a2+?+γnan,εγ=γ1γ2?γn\gamma =(\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})\in \{\pm 1\}^{n},b_{\gamma }=a_{0}+\gamma _{1}a_{1}+\gamma _{2}a_{2}+\cdots +\gamma _{n}a_{n},\varepsilon _{\gamma }=\gamma _{1}\gamma _{2}\cdots \gamma _{n} 从仅有 ak" role="presentation">aka_{k} 一个参数,硬生生地加到 ak,γ,bγ,εγ" role="presentation">ak,γ,bγ,εγa_{k},\gamma,b_{\gamma },\varepsilon _{\gamma } 四个参数,运算有幂、阶乘、累乘、累和,甚至还包含符号函数 sgn,实在是…… 复杂又丑陋。 哦对了,如果你增加附加因子 2cos⁡(x)" role="presentation">2cos?(x)2\cos(x) ,那么这个序列一直坚持到 k=55" role="presentation">k=55k=55 ,即: ∫0∞2cos⁡(x)sin⁡(x)xsin⁡(x/3)x/3...sin⁡(x/111)x/111dx=π2" role="presentation">∫0∞2cos?(x)sin?(x)xsin?(x/3)x/3...sin?(x/111)x/111dx=π2\int_{0}^{\infty}2\cos(x)\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}...\frac{\sin(x/111)}{x/111}\mathrm{d}x=\frac{\pi}{2} 都完全没毛病。 就在你以为大功告成,可以擦一擦额头上的汗时,下一秒…… ∫0∞2cos⁡(x)sin⁡(x)xsin⁡(x/3)x/3...sin⁡(x/113)x/113dx<π2" role="presentation">∫0∞2cos?(x)sin?(x)xsin?(x/3)x/3...sin?(x/113)x/113dx<π2\int_{0}^{\infty}2\cos(x)\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}...\frac{\sin(x/113)}{x/113}\mathrm{d}x\int_{0}^{\infty}2\cos(x)\frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}...\frac{\sin(x/113)}{x/113}\mathrm{d}x<\frac{\pi}{2} 波尔文积分这个数学例子在某种程度上其实证明了一个老生常谈却又时常被人们用侥幸心理无视掉的道理: 直觉和经验,其实并不总是那么可靠。 |
|
一元四次方程的求根公式,参考 一元四次方程_百度百科?baike.baidu.com/item/%E4%B8%80%E5%85%83%E5%9B%9B%E6%AC%A1%E6%96%B9%E7%A8%8B#:~:text=%E4%B8%80%E5%85%83%E5%9B%9B%E6%AC%A1%E6%96%B9%E7%A8%8B%E6%B1%82%E6%A0%B9%E5%85%AC%E5%BC%8F%287%E5%BC%A0%29.,%E4%B8%80%E8%88%AC%E7%9A%84%E4%B8%80%E5%85%83%E5%9B%9B%E6%AC%A1%E6%96%B9%E7%A8%8B%E5%8F%AF%E4%BB%A5%E9%80%9A%E8%BF%87.%20%E7%9A%84%E4%BB%A3%E6%8D%A2%E6%B6%88%E6%8E%89%E4%B8%89%E6%AC%A1%E9%A1%B9%EF%BC%8C%E5%BE%97%E5%88%B0%E4%B8%80%E4%B8%AA%E4%B8%8D%E5%90%AB%E4%B8%89%E6%AC%A1%E9%A1%B9%E7%9A%84%E5%9B%9B%E6%AC%A1%E6%96%B9%E7%A8%8B%EF%BC%8C%E7%84%B6%E5%90%8E%E7%94%A8%E9%85%8D%E6%96%B9%E6%B3%95%E6%B1%82%E8%A7%A3%EF%BC%88%E8%BF%99%E9%87%8C%E7%9A%84%E9%85%8D%E6%96%B9%E6%8C%87%E7%9A%84%E6%98%AF%E9%85%8D%E5%B9%B3%E6%96%B9%EF%BC%89%E3%80%82 |

|
|
百度百科上的公式是用 Δ1,Δ2,Δ" role="presentation">Δ1,Δ2,Δ\Delta_{1},\Delta_{2},\Delta 一层一层套的,然后我花了一个小时把无 Δ" role="presentation">Δ\Delta 版的求根公式打了出来,真的很恶心.后面的公式都是我用LaTeX打出来的,所以别指望双击把它放大,在此我也要对我以前不经意间的骗赞行为道歉。 若 ax4+bx3+cx2+dx+e=0,a,b,c,d,e∈R,a≠0" role="presentation">ax4+bx3+cx2+dx+e=0,a,b,c,d,e∈R,a≠0ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a,b,c,d,e\in\mathbb{R},a\neq0,则:x1=−b4a−12b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)−12b24a2−4c3a−(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)−−b3a3+4bca2−8da4b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)" role="presentation">x1=?b4a?12b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)?12b24a2?4c3a?(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)??b3a3+4bca2?8da4b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)x_{1}=\frac{-b}{4a}-\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})} -\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{4c}{3a}-(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a}) -\frac{-\frac{b^{3}}{a^{3}}+\frac{4bc}{a^{2}}-\frac{8d}{a}}{4\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})}}} x2=−b4a−12b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)+12b24a2−4c3a−(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)−−b3a3+4bca2−8da4b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)" role="presentation">x2=?b4a?12b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)+12b24a2?4c3a?(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)??b3a3+4bca2?8da4b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)x_{2}=\frac{-b}{4a}-\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})} +\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{4c}{3a}-(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a}) -\frac{-\frac{b^{3}}{a^{3}}+\frac{4bc}{a^{2}}-\frac{8d}{a}}{4\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})}}} x3=−b4a−12b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)−12b24a2−4c3a−(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)+−b3a3+4bca2−8da4b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)" role="presentation">x3=?b4a?12b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)?12b24a2?4c3a?(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)+?b3a3+4bca2?8da4b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)x_{3}=\frac{-b}{4a}-\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})} -\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{4c}{3a}-(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a}) +\frac{-\frac{b^{3}}{a^{3}}+\frac{4bc}{a^{2}}-\frac{8d}{a}}{4\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})}}} x4=−b4a−12b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)+12b24a2−4c3a−(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)+−b3a3+4bca2−8da4b24a2−2c3a+(23(c2−3bd+12ae)3a(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23+(2c3−9bcd+27ad2+27b2e−72ace)+−4(c2−3bd+12ae)3+(2c3−9bcd+27ad2+27b2e−72ace)23323a)" role="presentation">x4=?b4a?12b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)+12b24a2?4c3a?(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)+?b3a3+4bca2?8da4b24a2?2c3a+(23(c2?3bd+12ae)3a(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23+(2c3?9bcd+27ad2+27b2e?72ace)+?4(c2?3bd+12ae)3+(2c3?9bcd+27ad2+27b2e?72ace)23323a)x_{4}=\frac{-b}{4a}-\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})} +\frac{1}{2}\sqrt{\frac{b^{2}}{4a^{2}}-\frac{4c}{3a}-(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a}) +\frac{-\frac{b^{3}}{a^{3}}+\frac{4bc}{a^{2}}-\frac{8d}{a}}{4\sqrt{\frac{b^{2}}{4a^{2}}-\frac{2c}{3a}+(\frac{\sqrt[3]{2}(c^{2}-3bd+12ae)}{3a\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}+\frac{\sqrt[3]{(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)+\sqrt{-4(c^{2}-3bd+12ae)^{3}+(2c^{3}-9bcd+27ad^{2}+27b^{2}e-72ace)^{2}}}}{3\sqrt[3]{2}a})}}} 看得清吗?这里有一个pdf版的(因为公式太长,我只能用A1纸): |
|
|
|
四次方程的求根公式.pdf 184.5K · 百度网盘 我放个图,这里非常感谢 @SCPMTF 为我提供的图片,并允许我在这里使用: |

|
|
是不是很长呢? ————分割线———— 众所周知,我是很鸽的,而且这个答案似乎没有可更的地方,所以.......[逃][doge] |
|
波尔文积分(英语:Borwein integral)是一种由波尔文父子发现的性质特殊的积分,常用于作为看似存在的数学规律最终失效的例子。2001年,大卫·波尔文(David Borwein)和乔纳森·波尔文共同发表了这个涉及sinc函数的积分 。 这里面有一个神奇的规律: |

|
|
一直走着走着,走到这里: |
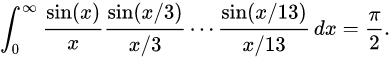
|
|
结果下一个就失效了: |
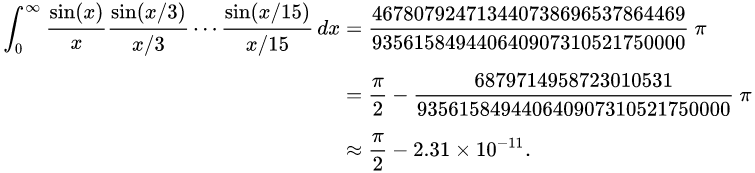
|
|
参考维基百科:Borwein integral |
|
有人提到说一元四次方程的求根公式很丑,我觉得不然,只要经过几次换元转为一个三次方程即可。 |
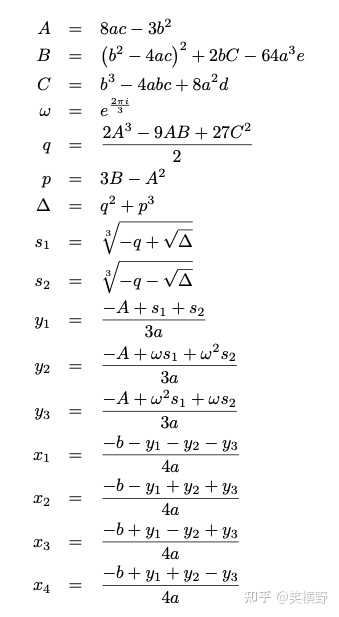
|
|
高斯通过计算 \cos \left(\frac{2\pi}{17}\right) 利用尺规作图画出了正17边形,同样地,正65537边形也是可以尺规作图画出来的,但是需要计算 \cos\left(\frac{2\pi}{65537}\right) 。公式极其复杂,一共由4059个公式组成,最后得到的是 \cos \left(\frac{2^{14}\pi}{65537}\right) ,通过角平分线很容易得到整个正65537边形。双栏pdf一共243页,节选几页如下: |

|
|
|
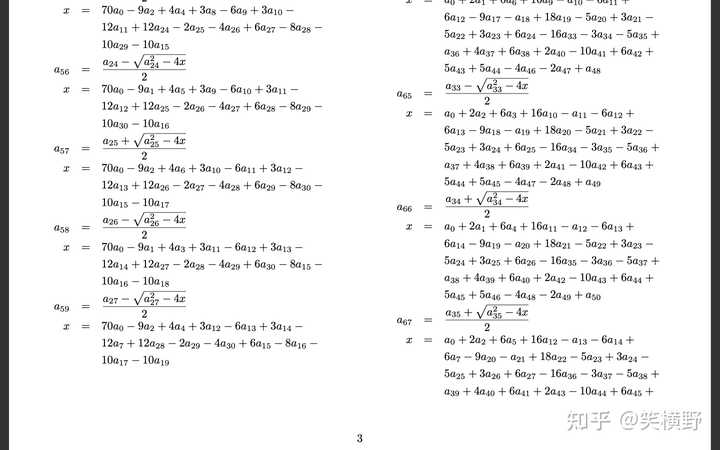
|
|
|

|
|
|

|
|
|

|
|
求解思路还算清晰,本质上就是求解一堆的一元二次方程,最后的结果让人不知道说什么好,只能说“丑”了。 ps: 公式全文见如下链接 |
|
如果你喜欢丑陋的公式,我建议你去看水力学教材,绝对量大管饱。 |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |