| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 6岁女儿问为什么负数乘以负数得正数,有啥通俗易懂的答案? -> 正文阅读 |
|
|
[时尚穿搭]6岁女儿问为什么负数乘以负数得正数,有啥通俗易懂的答案? |
| [收藏本文] 【下载本文】 |
|
矢量什么的她肯定接受不了,有啥生活中孩子能理解的答案么 |
|
比较通俗的理解方式: 你每天赚两块钱,三天以后比现在多六块钱,这是 2x3=6 你每天亏两块钱,三天以后比现在少六块钱,这是 (-2)x3=-6 你每天赚两块钱,三天以前比现在少六块钱,这是 2x(-3)=-6 你每天亏两块钱,三天以前比现在多六块钱,这是 (-2)x(-3)=6 |
|
负的意思是相反 相反然后再相反,所以跟原来方向一样 所以就是正数了 |
|
第一天:你看这是一个人,乘负数就是转了180度,转两次就正过来了 第二天:爸,我发明一东西,乘他相当于转90度 |
|
孩砸,你看,在复平面内,向量乘以负一,就是旋转180度,所以连续左乘两次负一,是不是就等于向量旋转一圈回到原点啊? |
|
你看,你有讨厌的人,是坏事 你看,有人死了,是坏事 但是,你讨厌的人死了,坏事X坏事 这就是好事儿了 |
|
答过这个,服从分配律其实才是乘法的本质,所以 (-A) × B + (-A) × (-B) = (-A)×(B + (-B)) = 0 (-A) × B + A × B = ((-A) + A) × B = 0 两式相减整理得到 A × B = (-A) × (-B) |
|
六岁,正是一个适合学习欧拉定理的年纪 。 负负得正的原因:(−1)×(−1)=eiπ⋅eiπ=e2iπ=1" role="presentation">(?1)×(?1)=eiπ?eiπ=e2iπ=1(-1)\times (-1)=e^{i\pi}\cdot e^{i\pi}=e^{2i\pi}=1 |
|
想象你现在站在一个数轴上的0点。 首先加减法用数轴很好理解,加法(或者正数)就是往数轴的右边(正数轴)走多少步,减法(或负数)就是往数轴的左边(负数轴)走多少步。 那么乘法呢? 比如a x b,a代表一步走几个格子,b代表走几步。(这个需要让孩子大概理解一下乘法的概念) 那么我们再引入负数的乘法: +a 代表朝向正数轴(右),-a代表朝向负数轴(左)。 +b 代表往前走,-b代表往后走。 |

|
|
来源 Infinity Learn NEET 先来算2x3,那么就相当于朝向右边,并且往前走3步,每步2格。答案显而易见是6。 |

|
|
来源 Infinity Learn NEET 如果是(-2)x(-3),那么相当于朝向左边,然后往后走3步,每步2格,同样得到6。 |

|
|
来源 Infinity Learn NEET 搞定! 如果孩子已经知道负数的加减法,能理解乘法和乘法交换律的话(不过估计6岁的孩子还理解不了,可以等大一点),那么还可以用这种方法: 先来看正数乘以负数: 我们已经知道5x3=15了,那5x(-3)=? 已知:5x【3+(-3)】=5x0=0 用乘法交换律:5x3 + 5x(-3)=0 所以:15+5x(-3)=0 所以:5x(-3)= -15 那么再来看负数乘以负数: (-2)x(-6)=? -2x【6+(-6)】= -2x0 = 0 -2x6 + (-2)x(-6)= 0 通过上面的推导我们已经得出正数乘以负数等于负数了,所以-2x6=-12 所以:-12+(-2)x(-6)= 0 所以:(-2)x(-6)= 12 |
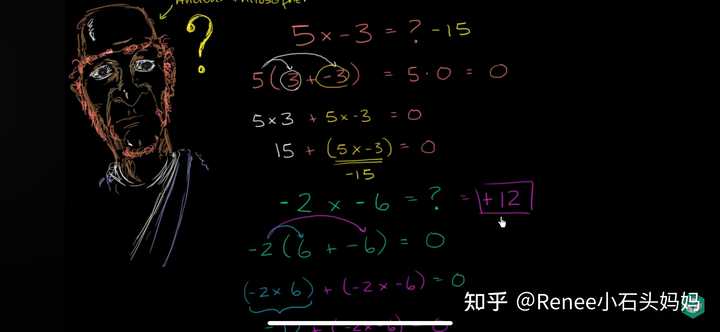
|
|
(来自Khan Academy的视频) |
|
负数带了方向的概念了。任何使用方向来解释负数的,都是恰当的。 其实虚数i也是一样,虚数i是方向转90度,乘两次变成-1,就是转180度,就掉头了。 乘四次,变成360度,也相当于乘了两次-1,相当于又会到了初始位置 |
|
看了高赞答案,回忆了一下我们数学老师当年给我们解释的,使用走路迈步来解释: 认为前面是正,后面是负,方向对应正负,步数和步长对应数值: 我面向前,走2步,每步3米,就是2*3=6; 我面向后,走2步,每步3米,就是-2*3=-6; 我面向前,走2步,但是每步后退3米,就是2*-3=-6; 我面向后,走2步,但是每步后退3米,就是-2*-3=6。 |
|
你拿了家里10万去做生意,结果一天赔了2万,5天就赔光了。你大哭,5天前要是不做这倒霉生意,老子至少还有10万。。。 -2 * -5=10 但是,这是解释给大人,至少是解释给大孩子的。 我家老大10岁四年级,刚学了个认识负数,校内要求是对负数的大小有个感知就够了。题主6岁的娃,教负数乘负数,是不是提前得太多了点儿? |

|
|
我并不排斥超前学习,但是我主张超前习内容的选择,应该与孩子的发展阶段相符合。 比如一岁多的娃,很多大人会他从1数到10,甚至有用这种和数学没有半毛钱关系的手势来教的。 |

|
|
娃凭着记忆力完全可以背得666,在众人面前出口成章,被惊为天人。但是那又怎样呢?首先他对数的理解不可能有多么的深入;其次,就算是他模模糊糊理解了,认识1~10,有什么了不起吗?1岁知道和3岁知道,没有什么本质的不同。 据国内外多项实际调查数据显示,孩子学习数学的起始年龄,对其未来的学习成绩和职业发展影响不大。 数学是一门高度抽象的学科,数学的学习是有认知能力门槛的。在年龄比较小的阶段拔数学,是非常低效的。三年级之前大量搞大语文、英语、并进行简单的地理历史启蒙,才是性价比更高的选择。况且现在各种适应该年龄段娃的动画、app、绘本,有趣有用的相关资源一抓一大把。 |

|
|
三年级之后娃的认知能力、抽象思维能力出来了,数学上难度,会乘风飞起,事半功倍。 关于各科的规划方式和路径问题,在我之前的文章里有详细的介绍,篇篇都是肝出来的,放在下面,收藏防丢。 关于学习理念、学习规划、学习路线 ↓↓↓: 家长都在焦虑个啥: 为什么幼儿园就要开始学习小学一年级的内容?家长们都在焦虑什么呢?79 赞同 · 13 评论回答 |

|
|
是否应该让孩子超前学习?11 赞同 · 0 评论回答 |

|
|
关于学习规划: 承认吧,普娃要想逆袭成为学霸,拼的就是爸妈!22 赞同 · 1 评论文章 |

|
|
一年级孩子应该怎么培养?110 赞同 · 6 评论回答 |
|
|
小学需要培养孩子的哪些学习习惯?35 赞同 · 2 评论回答 |

|
|
是否让小学的孩子提前学习初中课程?有必要没?19 赞同 · 7 评论回答 |

|
|
关于大童英语启蒙: 孩子快升三年级了,对启蒙或培养孩子的英语兴趣有哪些建议?62 赞同 · 9 评论回答 |

|
|
关于古诗文学习路径: 古诗文3~12岁保姆级攻略|经验、路径、方法、技巧、资源一站配齐40 赞同 · 16 评论文章 |

|
|
关于写作方法论: 孩子学习阅读和写作的知识有什么好处?7 赞同 · 5 评论回答 |
|
|
语文试卷的作文题目为《我家的小狗》,孩子因为家里没有养狗没有写作文,作为成年人你持什么态度?47 赞同 · 2 评论回答 |

|
|
关于要不要学奥数: 小学阶段的奥数是必须学的吗?22 赞同 · 0 评论回答 |

|
|
关于要不要学编程: 孩子对编程感兴趣,我一个月 3000 元没能力支持孩子学习这个费钱的爱好,如果是你会给孩子买课吗?379 赞同 · 50 评论回答 |

|
|
@知乎亲子 |
|
看了这个问题,我第一时间不是想着怎么给孩子解答,而是不由自主地发出一声惊呼,六岁的孩子已经知道这么多了!! 同样都是孩子,为什么区别这么大?! 我女儿也马上六岁了,她从来也没有疑惑过为什么负数乘以负数可以得到正数? 她那个小脑瓜里装的是什么呢? 恐怕只有: 海底小纵队我今天可以看几集! 叶罗丽又出了什么新的卡片! 还能不能说服妈妈再买一个蛋仔玩具! 今天已经吃了一颗糖了,怎么才能骗着爸爸再给我一颗而不是妈妈知道? |

|
|
别说负负得正了,她连负数是什么都不知道! 她跟“负”这个字唯一的关联恐怕就是坐电梯时纠结应该按负一还是按负二! 因为负一放着我们家的电瓶车,那是我们俩最喜欢的代步工具! 我想让现在的她理解负负得正,恐怕比蜀道还难! 我看还是让她熟练掌握十以内的加减法比较现实! 而后者对现在的她来说也是一座难以逾越的山峰! 有一天我随口问她6+2等于几,她马上流利的回答我是8! 我大为惊喜地向她爸爸交换了一下眼神,那意思就是咱孩子是个天才呀! 6+2=8我可从来没有教过她,她是怎么知道的! 既然是天才,那我可得好好培养了,举一反三是必须滴! 于是我笑眯眯地问她,那8-2等于几? 或许是我掩饰不住的笑意给了她信心,她信誓旦旦地告诉我等于4! 答完我没吭声,她扭头看看我脸色似乎有点儿不对劲儿,马上笑着试探,等于3? 那一刻我明白了,这就是个普通孩子! 幻想她是个小天才的亲妈滤镜,还是早点碎了吧! 跟知道负负得正的孩子像比,恐怕我得气死! 好在我知道她原本没学过这些,只顾着天天在外面放羊了,所以我倒不是特别着急! 我还抱着一丝幻想,孩子越大,学习能力、理解能力越强,等她开始学起来说不定很快就能掌握了! 她不知道负负得正,但她知道哪里的户外场所设施最全,她知道哪个滑梯滑起来更刺激,她知道哪里的攀爬架最有挑战,她知道哪个公园能遇到更多小朋友! |

|
|
她知道怎么给爸爸设圈套才能把谈话内容引到巧克力上,也知道怎么暗示妈妈给自己送惊喜。 |
|
|
她会在爸爸刚要掏出手机准备刷一会儿时及时的递上一本绘本,也会在妈妈忙着写作没有管她时戏精附体,带着哭腔大声控诉,我可是你最亲爱的孩子呀,你为什么一点都不管我! |

|
|
跟博学多识的天才牛蛙相比,她就是个妥妥的普娃,还满脑子只想着玩,没有一点上进心。 当我看着她为了到高高的大桥体验下坡的乐趣而一路冲锋时,看着她飞快地从高高的坡上一边向我冲过来一边叫妈妈时,我觉得她好帅气,我好爱她! |

|
|
0 我不知道怎么给现在的她科普更多的数学难题,但我知道一辈子很长,学习的日子那么多,自由肆意的快乐却很奢侈,我愿意陪她多享受一会儿。 |
|
这要从负数的本质说起,负数跟正数,表示相反的量。 其实现在很多小学课本在引入负数时,使用的温度计模型不太理想。 因为零上和零下并没有明显的区分,而且都是温度,并不是相反的【量】,不表示相反的意义。 |

|
|
如果用收入和支出的模型、收益和欠债的模型是比较理想的。 贴近生活,好理解,意义相反,正好可以解释负数的运算。 比如,收入1000元是+1000,而负债1000是-1000,没有收入也没有负债是0。 于是正数和负数可以在0两边铺开。 那么正负数的运算,也好说了。 |

|
|
1+(-1)=0因为负债和收入抵消了。 1+(-6)=-5因为负债太多了,收入1个得拿去还,现在还了1个还剩5个没还,还是负数。 5+(-2)=3因为收入足以还上负债,然后还剩3个。 5*(-5)=-25因为乘法是连续的加,你连续加了五次(-5),不是(-25)是什么呢? -5*(-5)=25,这里的(-5)不能表示5次了,哪有负数表示5次的?这里的(-5)就是一个相反的量,负债是5,那这里有两个负号,不是又“负”了一次嘛,那岂不是把原本相反的量再反过来吗?就是正的,负负得正。 (-2)-(-3)=1,也是这个道理。 而负数除以负数,比如(-6)÷(-6),也是得正的,为什么? 因为除以一个数等于乘以这个数的倒数,(-6)的倒数是(-1/6),这又回到乘法上来了! |

|
|
你看,从相反的量来引入负数,孩子好理解,也好做计算了。 负负得正,简单来说就是相反的量,添加一个负号,再把它的意义反过来了。就像方向,本来在左边,现在反一下,到右边了。 其实也可以用方向来表示,左边是负,右边是正。这样解释起来也简单。 |
|
此时可出家长终极技能:“等你长大你就懂了”。 |
|
前几个回答真的有一丁点和孩子交流的经验么。。什么群魔乱舞,简直是彰显我国孩童教育有多拉胯的一个个新鲜例证。。感觉需要这个答案的不是这个6岁小孩儿而是你们。。 孩子是靠感官去认知这个世界的。她肯定是听到了类似“正正得正、正负得负、负正得负、负负得正”的口令,光这几个字她就无法清晰感知,已经够在她脑海里拧成一团乱麻了,别再付诸更多的文字定义了。。 怎么做?很简单,让她看,用眼睛去看 伸出手来,手掌朝上,“你看,我现在手是正的” “负呢,就是把手翻过来”,你把手翻成手背朝上,“正呢,就是不翻” 然后你挨个给她演示一遍,“现在我们一开始手掌在上” “正,正”不翻,“得正,对吧”,手掌朝上 “正,负”翻一次,“得负”,手背朝上 “负,正”翻一次,“得负”,手背朝上 “负,负”翻两次,“得正”,手掌又朝上了 你甚至都不用去跟她严谨定义什么最后手掌朝上是正、朝下是负,她用眼睛已经先于理性思维,感知到这层逻辑,“噢噢我懂了!”脱口而出,对于她的年纪和认知来说,这就够了 至于她有没有真正理解不重要,重要的是以后在她需要完全理解这个逻辑的时候,这一段视觉记忆会帮她理清思绪的乱麻 就算对大人,讲解概念的时候也尽量少扯定义,而是用直觉的例证去引导对方自发地推导出定义。我凸优化讲到局部最优的时候都多余张嘴说,就简单画个鞍点的图拿个小球在上面滚呀滚,你大爷的讲个负数都要扯一堆。。信不信到老年痴呆的那一天你都忘了负数是啥,却还能记起翻两次的手掌,和停在鞍点上的小球。。 |

|
|
你女儿落伍太多了,现在3岁的学习状态是这个 |
|
孩子:为什么负数乘以负数等于(得)一个正数? 你:这可以有很多解释,比如 1 是整数环的单位元,比如负号代表数轴上的反向。 孩子:可是对于这些,一是我都不懂,二是我凭什么接受这些理论呢?有没有我能听懂的解释呢? 你:那我们可以试一试。首先,我们需要知道,数是人们构造出来的。最简单朴素的构造,就是人掰手指头构造出了正数。负数同样也是人们构造出来的。我们当然不止有一种构造方法,但这些构造方法之间有好坏之分。我们肯定会保留好的构造方法,摒弃坏的构造方法吧? 孩子:对的。 你:你问了“负数乘以负数为什么等于正数”,那我们就先看看我们把数的概念从正数扩展到正数、0 和负数时,我们希望等式有什么不变的性质。我希望:如果 a×c=b×c" role="presentation">a×c=b×ca \times c=b \times c 且 c≠0" role="presentation">c≠0c\neq 0 ,那么两边同时除以 c" role="presentation">cc ,得到 a=b" role="presentation">a=ba=b 。这个你认同吗? 孩子:认同。 你:那我们开始尝试一些可能。我们首先希望一种运算是尽可能广泛的:如果正数只能与正数相乘,负数只能与负数相乘,那就不够理想。 孩子:是不够理想,但如果其他的方法都构造不出来呢? 你:当然如果我们发现其他的路都行不通,那也只能这么办,只是我们足够幸运,在几千年前就发现真的有更好的路。我们先看看正数乘以负数等于什么。我们先定义它是正数,那么 −a×b=a×b" role="presentation">?a×b=a×b-a \times b =a \times b ,根据我们前面对等式性质的假设,那么 a=−a" role="presentation">a=?aa=-a 。这也就是说,我们定义的负数和以前的正数是一样的,什么也没有增加,和没定义之前没有区别。因此这种定义是不好的。 孩子:确实不好。 你:然后我们看负数乘以负数,我们就假定它是负数,看看怎么样: (−a)×(−b)=−a×b" role="presentation">(?a)×(?b)=?a×b(-a)\times (-b)=-a \times b ,两边同时除以 −a" role="presentation">?a-a ,得到 b=−b" role="presentation">b=?bb=-b ,所以也没有定义出什么新东西。当然严格地说,我们这里还假定了交换律:你也认同交换律是我们应该保留的乘法性质吧? 孩子:是的。 你:所以剩下的可能就是 (−a)×(−b)=a×b" role="presentation">(?a)×(?b)=a×b(-a) \times (-b)=a \times b 了。 孩子:那这个定义一定好吗?有没有可能也存在一些其他定义方法里存在的问题? 你:这是个好问题,因为我们前面只说明了其他方法不好,没说明这个方法就一定好。要说明它一定好,那就需要验证如果我们使用这个定义,那么四则运算中的所有其他性质都保持是好的。以后我们可以看到,如果其他定义也合理拓展到负数时,还真是这样。 孩子:那还真是很神奇。 你:对的,数学就是一种很神奇的东西。以后等你学到了实数和复数,还有更神奇的东西呢! 如果读者有进一步的兴趣,请参考: 第二十章:数、直观与时空11 赞同 · 74 评论文章 |
|
根据负数的定义, 1+(-1)=0 两端同乘-1, -1×(1+(-1))=(-1)×0 左端分配率打开, 右端根据0的性质, -1×1+(-1)×(-1)=0 左端第一项根据1的性质, -1+(-1)×(-1)=0 移项, (-1)×(-1)=1 有了这一条之后可以显然地根据结合律, 交换律等推广到任意数上, 都有(-a)×(-b)=ab 评论区有读者敏锐地指出-1×1=1 (更广范地, "负正得负" ) 这件事情在以上过程里用到了, 但其实是没有证明的. 这里补充一下证明: 根据负数的定义, -1+1=0 两端同乘1, 1×((-1)+1)=1×0 左端分配率打开, 右端根据0的性质, 1×(-1)+1×1=0 左端第二项根据1 **在非负数乘法中** 的性质, 1×(-1)+1=0 移项, 1×(-1)=-1, 根据乘法的交换律也可以得到另一种顺序下的结果. 有了这一条之后可以显然地根据结合律, 交换律等推广到任意数上, 都有(-a)×b=-ab 由此完成了 "正负得负" 的证明, 在有了这一段之后就可以开始做开头那段的证明了. 这个解释对一般6岁小孩子肯定不算通俗易懂 (不过一般6岁小孩子为啥会思考负数乘法...) , 主要是为了反驳 (指正) 一下其它回答 "规定如此" 的答案. 当然确实可以说这是定义, 但即便如此这个定义也不是任意选的. 只要你还想要你的乘法 1.是非负数乘法的拓展; 2.满足分配率, 结合律, 交换律等重要的性质, 那么合理的定义就只有这一种. 如果你定义(-1)×(-1)=-1; 或者添加新数定义(-1)×(-1)=(-1)^2把它设计成像个新素数一样, 都迟早会出现不符合我们所习惯的运算律的情况. 在这个意义下, 倒不如说我们是 "推导出了这个运算法则" . 不过答主可以还是试着把这个解答给孩子讲一下, 说不定能培养出一个布尔巴基传承() |
|
正数表示朋友,负数表示敌人,敌人的敌人就是朋友 |
|
最通俗易懂的答案是,不要给6岁的孩子讲负数乘法。 因为教育心理学上认为,负数乘法运算是抽象的数学概念,是儿童数学认知的第四阶段,12岁以上的孩子才开始理解的概念。 6岁的孩子处于第二阶段,前运算阶段。孩子开始能够用符号或象征来代表事物,但他们的思维通常是直观的、具体的,无法理解抽象的概念。所以标准课纲要求幼儿园不学习计算,要到小学才学习,就是因为教育心理学认为6岁这个阶段还能不理解复杂运算。 负数这个概念是可以讲的,因为有零下的温度计。需要注意,温度计的零下和真正的负数概念不一样,只是个定义。-6℃在温度计上依然是一个直观的事物,不是欠账那样的抽象概念。所以6岁孩子理解的温度计负数和数学上的负数也是不一样的。 所以可以讲负数,不应该讲负数抽象运算,因为这不但涉及了乘法运算,还涉及了抽象的负数概念,属于教育心理学上12岁以上孩子接触的内容,根本不适合讲给6岁的孩子听。 你想要给6岁的孩子超前教育,最多到第三阶段,具体运算阶段就行了。跳到第四阶段抽象概念运算的话,不是通俗易懂就能解释的问题,而是孩子大脑还没发育到那一阶段,没有那个功能啊。 你知道,孩子在2岁以前会尿床,但在3岁以后尿床次数就减少了。是因为孩子找到通俗易懂的道理了吗?不是,是因为孩子在2-3岁的时候神经系统发育了,他们能控制尿床了。 你孩子在2岁的时候就能学会双脚跳,四五岁才能学会单脚跳。这不是因为你给孩子找到了通俗易懂的答案。是因为四五岁运动神经才能发育出精细运动的能力,才能单脚跳。 所以孩子的教育是要根据神经系统和思维能力的发育同步进行的,不能超前教育。 我会在后面补上教育心理学皮亚杰的四个阶段理论供你参考。 如果你能看懂,那么就不会纠结给6岁的孩子讲抽象数学概念,这其实是一种虐待。 如果你看不懂,一定要找个通俗易懂的例子想要教给孩子的话,那请记住:马戏团的狗也能算加减法,这不是因为训犬师找到了通俗易懂的案例,而是用皮鞭让它们记住了3+2需要叫5声。 在教育心理学中,根据皮亚杰的儿童认知发展四阶段理论,孩子在每个阶段可以掌握的数学知识是不同的。以下是一个大致的概述: 第一阶段:感知运动阶段(0-2岁)。在这个阶段,孩子主要通过感觉和动作来了解世界,因此他们还不能真正掌握数学概念。 第二阶段:前运算阶段(2-7岁)。在这个阶段,孩子开始能够用符号或象征来代表事物,但他们的思维通常是直观的、具体的,无法理解抽象的概念。在这个阶段,孩子可以开始学习一些基本的计数和比较大小等数学知识。 第三阶段:具体运算阶段(7-12岁)。在这个阶段,孩子的思维逐渐从具体的事物转向抽象的概念,他们可以开始理解更复杂的数学概念,如加减乘除、分数、小数、算数、几何、概率等。 第四阶段:形式运算阶段(12岁以上)。在这个阶段,孩子的思维已经非常抽象,他们可以开始解决更复杂的数学问题,如代数、微积分等。 需要注意的是,每个孩子的认知发展速度和程度都是不同的,因此他们掌握数学知识的速度和程度也会有所不同。此外,教育方法和教师的引导也会影响孩子掌握数学知识的速度和程度。因此,家长和教育者需要根据孩子的实际情况和需要,采用适当的教育方法和策略,帮助孩子更好地掌握数学知识。 世上有天才的孩子,天才们确实可以在6岁就掌握形式运算。但如果你的孩子6岁听不懂负负得正,那么她就不是天才,不要用训犬师的方法去教她。 |
|
乘法的底层是加法, 想要真正理解负数乘法,就要理解负数加法, 当然,首先要理解负数,否则各种例子只会让你女儿似懂非懂, 1、理解负数,如3和-3的区别 2、理解负数加减法,如3+(-3)和3-(-3)的区别 3、理解负数乘法,(-3)*3相当于(-3)+(-3)+(-3),而(-3)*(-3)相当于-(-3) -(-3) -(-3) 记住,加减乘除的底层都是加法,无论正负 |
|
孩子才六岁,一个上幼儿园年龄的小朋友,这样的数学概念,她是很难搞懂的,所以,你还不如直接跟她说: “这个知识点,现在我跟你说了,你也不会懂,但是,等到你长大以后,学过了许多知识以后,你自己就会懂的。” 年龄不同,懂得的知识也不同,能够理解的知识更不同,这个年龄段的孩子,你再怎么和她解释,她都不可能理解为什么负负得正。不要说一个孩子,即使是一个没有读过书的成年人,你想和他解释清楚负负得正的原理,也是相当困难的。 |

|
|
我也经常被小朋友的提问难住,每当被他们难住的时候,我都会如实的告诉他们: “这个问题我也不知道诶,我得查资料以后再告诉你们。” 然后我会尽量用小朋友懂的原理,告诉他们答案。 |

|
|
比如有次小朋友问我冲击波的问题,我为他们读了词条以后,又找了电视给他们看,爆炸以后,气浪会把人掀出去,这个气浪就是冲击波。 后来有知友提醒我,可以运用击掌打灭蜡烛的表演,来让孩子直观地感受到冲击波是什么,我觉得这个主意就很棒。 |

|
|
但是有更多的知识,其实我们尽量解释了,小年龄段的孩子也不可能懂。因此我们不妨跟他们说实话,告诉他们: “学知识就像爬楼梯,你如果不从第一步开始,就不可能爬到最顶上。知识也是这样的。” 如果孩子提出的问题,父母也不知道答案。可以大大方方的告诉孩子,在儿童面前承认自己的不足,和孩子一起去寻找答案。 这等于在告诉孩子:每个人都有不懂的问题,只要我们想办法,就会找到答案,人的知识的宽度和广度,是在不断的学习过程中慢慢积累的。 儿童解决问题的能力,通过一个能积极配合其学习的成人,能够得到更快的提升,而且会在近期单独活动中,积极主动的去思考。 我们要让孩子知道,我们所学的知识,是许多人研究总结的成果,我们是站在前人的肩膀上前行。 |
|
别人家6岁女儿都在问负数乘以负数了,我们家7岁半了乘除法都还算不称头。 昨天口算,2÷2=0,我.......佛慈悲。 专注自家,切勿拉踩,理智带娃,言归正传。 其实负数这个问题,我在孩子4岁多的时候就跟她有过讨论。 不是要教她什么知识,单纯是她看到电梯按钮的“-1”,问我1前面为什么有一个“-”。 |

|
|
所以就跟她解释了一下,负一在楼层里的含义: 我们把地面作为作为往上建楼的起点(就是“0”楼),高于起点的就是正楼,高于1楼就是“+1”,也就是按钮上的“1”;低于起点的就是“负”楼,低几层就是负几楼。 比如低1层,是“负一楼”;低2层,就是“负2楼”。 然后就此打住,没有深入。 后面冬天去玩雪,大人讨论气温的时候,说到“零下几度”,就又顺便给孩子解释了一下“0度”是人为规定的温度,低于“0度”的就是“零下几度”,也就是“负几度”。 之后买了数学启蒙绘本,专门有一本书讲“0”的概念和生活中的各种意义,孩子对“负数”的理解又深入了一点。 就是这套: |

|
|
里面有一本专门讲“0”的各种实际意义 如果在对“0”和负数的意义比较了解的情况下,我觉得可以用坐电梯的例子来浅显地解释,不知道能不能行得通,权作抛砖引玉吧: 比如(-2)*(-2)=4 2代表2层楼,+2如果代表往上2层楼,-2就代表往相反的方向也就是往下2层楼。 我们从地面开始坐电梯。 (-2)*2就表示往下坐2层楼,连着坐2次,也就是往下4层楼,到了“-4”楼。 (-2)*(-2)就表示往(-2)相反的方向坐2次,也就是往上4层楼,到了“4楼”,就是正数啦。 我感觉6岁能解释到这就够了,甚至觉得9岁以前解释到这都够了。 数学的学习和语文英语完全不一样。 如果用建房子来表示,语文英语可以随便从哪一楼开始修。 比如可能幼儿园就背完小学生必背古诗词了,但是还不识字;比如英语可以流利地听说了,但是最简单的hello都不认识。 但是数学不行,只能从地基开始一点一点搭。 你没有理解数和实物的对应,哪怕会从1数到100也只能是唱数,不能表示你明白“1”的真正概念;如果没有理解加法是什么,乘法你就学不懂。 关键数学的地基还很多,这座房子修完了,学另一个概念的时候又要重新从地基开始搭。 |

|
|
我是 @柠檬不萌 ,家有2年级慢腾腾小蜗牛一只,爱遛娃爱分享,欢迎关注~ @知乎亲子 |
|
负负的正是由含有幺元的代数环的定义得到的,简单的讲就是公理,规定的。不过如果想通俗的解释可以这么来: 为了证明对于数 a ,有 -(-a)=a : 由于实数加上加法是交换群(你不用和你女儿说这个),有 a=a+0 同时有因为交换群有逆元(你不用和你女儿说这个),有 -a+(-(-a))=0 ,这里需要告诉她一个概念,引入负数以后,对于任何一个数,都能找到一个数与其相加为零,所以 -a 当成一个数,不能把它理解为 0-a 于是有: a=a+0=a+(-a+(-(-a)))=(a+(-a))+(-(-a))=0+(-(-a))=-(-a) 好了,这样就证明了两个负一相乘是正一,别的数字就当加上系数即可。 |
|
先给他讲复平面的知识:复数乘积就是模相乘,幅角相加,然后 |

|
|
以上《数学女孩2》 |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |