| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 时尚穿搭 -> 阿基米德和国王下棋,要求用米填满 64 个方格,国王最后是怎么解决的? -> 正文阅读 |
|
|
[时尚穿搭]阿基米德和国王下棋,要求用米填满 64 个方格,国王最后是怎么解决的? |
| [收藏本文] 【下载本文】 |
|
阿基米德 |
|
这个问题在雅?依?别莱利曼的《趣味代数学》里有提到。 国王的解决方案是:要阿基米德自己去数,一粒不许多,一粒不许少。 |
|
阿基米德之所以活到75岁,就是因为他不会像哥们你这样问国王要怎么解决这个问题。 |
|
落子有神曰景,棋力千钧曰景,抡盘如飞曰景,一击爆头曰景,打死勿论曰景。 |
|
很简单。 赌局当天,放第一格的米。 过1天,放第二格的米。 再过2天,放第三格的米。 再过4天,放第四格的米。 …… 以此类推,每次在格子里放米的间隔时间为前一次的2倍。 想拿走全世界的米,总要有点等待的耐心。 |
|
国王: 第一个格子的米,就直接给你啦 第二个格子,你得转发给一个朋友帮你砍一刀 第三个格子,你得转发给三个朋友…… 诶阿基米德你别走呀,这米又不是不给你! |
|
国王:负溢出了 你欠我1粒米 |
|
国王:你看这棋盘是什么做的? 阿基米德:原木啊,国王,怎么了? 国王:原木,那就是log咯,每天多一倍,就是log2(64),也没多少嘛! |
|
守序善良:亲爱的阿基米德,很抱歉我暂时拿不出这么多米来,请允许我在你的余生里慢慢支付吧,保证你衣食无忧。 守序中立:对不起做不到。你看,让你来放,一个格子也放不下那么多米是吧,这样吧,我给你换一个精选奖励自选包。 守序邪恶:我知道你很急但是你先别急,我隔一天给你一粒,隔两天给你两粒,隔四天给你四粒,下一次拿几粒,中间就隔几天,来日方长。 中立善良:不管你是阿基米德,还是什么其他人;要米也好,要麦子也罢;反正你自己去数吧,一粒一粒数到满意为止。 绝对中立:阿基米德没干过这件事,他也没玩过什么国际象棋,这原本是套在古印度头上的故事,所以问题不成立,不需要回答。 中立邪恶:既然你阿基米德可以穿越,那我国王也穿越一把。你看这棋盘是原木(log)做的,那我们就按以2为底数的对数来给吧。 混乱善良:水稻我们历史的发展比较长,产业农民比较丰富。我们实施水稻战略是想在调整布局中提高农业水平,做好节能减排,搞好循环经济发展……别问了别问了。下一任国王一定会有办法的。 混乱中立:BYD我们叙拉古有水稻吗?我宣布奖励已经发放完毕,谁再问怎么办,谁就是造谣。 混乱邪恶:阿基米德,你看,背后是谁来了? |
|
行 慢慢给呗 第一天给一粒,然后再过两天给两粒,再过4天给4粒。每个格子准备米的时间都是上一个格子的两倍。没毛病吧 |
|
刘启:胜利,不一定要在棋盘上获得 |

|
|
|
|
在古印度有个叫锡塔的大臣,他聪明过人,发明了一种棋子,国王百玩不厌,于是决定重赏锡塔。锡塔说:“陛下,我只要一点大米。请您让人将麦子放在我发明的棋盘的六十四个格子内,第一格放一粒,第二格放二粒,第三格放四粒,第四格放八粒,第五格放十六粒……照这样放下去,每格比前一格多放一倍麦粒,直到把六十四个棋格放满就行了。” 国王听了哈哈大笑,他觉得锡塔这个人真是有趣,放着金银财宝不要,反而提出这样一个“笨”要求,谷仓里的大米多着呢,填完六十四个棋格实在是小意思。于是便传令粮食大臣:“答应锡塔的要求,现在就从粮库把大米拉过来。”在场的每一个人都认为一小袋大米就能填满棋盘上的十几个方格,一些人甚至忍不住笑了起来。 大米被拉来后,粮食大臣一粒一粒地填了起来。一粒、两粒、四粒、八粒……一开始,前面的几个方格很快就被填满,而此时还没有用完一小碗大米。但是慢慢地,所用的大米开始明显多了起来,三十二粒、六十四粒、一百二十八粒、二百五十六粒、五百一十二粒、一千零二十四粒…… 随着放置大米的方格不断增多,搬运大米的工具也由碗换成盆,又由盆换成箩筐。即使到这个时候,大臣们还是笑声不断,甚至有人提议不必如此费事了,干脆装满一马车大米给锡塔好了! 可不知从哪一刻起,喧闹的人们突然安静下来。因为往第16个方格上放米粒时,就需要拿出1公斤的大米,而到了第24格时,则需要满满一手手推车的米。如此看来,国王根本无法提供足够的大米放在棋盘上的第64格上去。大臣们和国王都惊诧得张大了嘴:即使把全国所有的大米都拿来,也填不满一个格子啊。 ~~~~~~~~~~~~~~~~~~~ 这时候国王说到:根据《民法典》第一百四十一条至一百五十一条规定,下列合同,当事人一方有权请求人民法院或者仲裁机构予以撤销 一,基于重大误解实施的 二,在订立合同时显失公平的。 三,欺诈 四,胁迫 重大误解,是指由于行为人在对行为的性质、对方当事人以及标的物的品种、质量、规格和数量等方面的错误认识,使行为的后果与自己的意思相悖,并造成较大损失情况下而为的民事法律行为。锡塔同志在当时的知识水平不高的背景下隐瞒奖励总数真相,使国王与在场的大臣对奖励总数形成了错误认识,即使穷尽全国的米都无法完成奖励,明显与国王的真实意思表示相违背,国王可以请求人民法院予以撤销该合同 诈骗罪,就是以非法占有为目的,用虚构事实或者隐瞒真相的方法,骗取款额较大的公私财物的行为。锡塔同志此处恶意隐瞒真相,有导致国王损失1~20格大米的现实的紧迫危险,已构成诈骗罪,数额特别巨大,社会影响恶劣,应处十年以上有期徒刑或者无期徒刑。但国王及时识破了锡塔的诈骗行为,没有造成损害结果,锡塔属于因意志以外的原因未得逞,成立诈骗未遂,可以比较既遂犯从轻或减轻处罚。故根据《刑法》第二百六十六条之规定,判处锡塔十年以上有期徒刑或者无期徒刑,并处罚金或者没收财产。 |
|
国王请来了大汉棋圣刘启 |
|
把阿基米德请到城堡 把赌约的米作为招待他的饮食 第1天,给1粒米 第2天,给2粒米 第3天,给4粒米 第4天,给8粒米 第5天,给16粒米 第6天,给32粒米 第7天,阿基米德要是还没饿死肯定也撑不住了吧,就不信不会主动要求修改赌约。 |
|
国王不必耍赖,他可以答应对方的要求,只要提一个条件:奖励如数交付,但是必须对方亲自验收。 米的总量约为1.845*10^19粒,如果每秒可以数5粒,数完需要1.17*10^11年,大约1170亿年 |
|
几十年后在遥远的东方,长安城内的汉太子刘启提供了一个教科书版的解决方案。 |
|
曹操向左慈曰:“我要龙肝作羹,汝能取否?” 慈曰:“有何难哉!”取墨笔于粉墙上画一条龙,以袍袖一拂,龙腹自开。左慈于龙腹中提出龙肝一副,鲜血尚流。 操不信,叱之曰:“汝先藏于袖中耳!” 慈曰:“脍必松江鲈鱼者方美。” 操曰:“千里之隔,安能取之?” 慈曰:“此亦何难取!”教把钓竿来,于堂下鱼池中钓之。顷刻钓出数十尾大鲈鱼,放在殿上。 操曰:“吾池中原有此鱼。” 慈曰:“大王何相欺耶?天下鲈鱼只两腮,惟松江鲈鱼有四腮:此可辨也。” 操曰:“如此妖人,必当除之!否则必将为害。” 遂命许褚引三百铁甲军追擒之。 |
|
“棋盘麦粒问题“的源头最早被记载于公元前18世纪,叙利亚的马里城出土的楔形文字板上: 一颗大麦粒,我增加了一颗大麦粒, 第一天成了2颗大麦粒; 第二天成了4颗大麦粒; 第三天成了8颗大麦粒; …… 第二十九天,成了1“千“ 3“百“ 48塔兰同 30明那 16 1/6舍客勒又2颗大麦粒 第三十天,成了2“千“ 7“百“37塔兰同 1/2明那 2 1/3舍客勒又4颗大麦粒。 (古代美索不达米亚常用为60进制,”千“=六十进位下的600,“百“=六十进位下的60,1塔兰同=60明那,1明那=60舍客勒) |
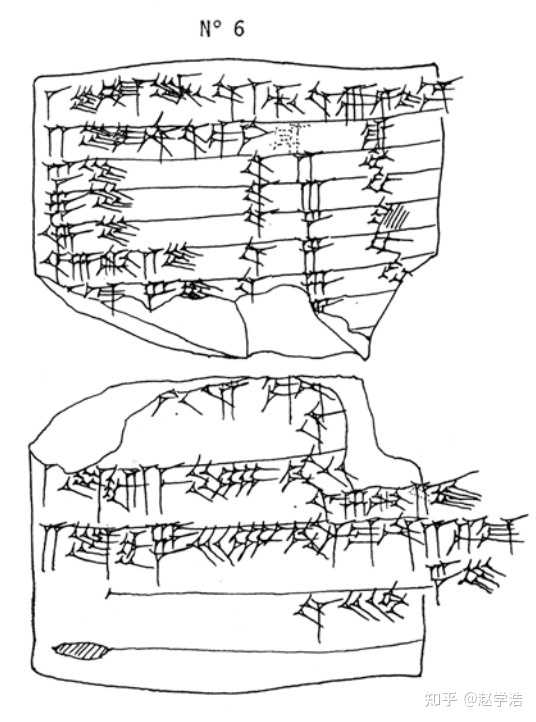
|
|
楔形文字板M 08613 如果按照一颗大麦粒0.05克计算的话,第30天将变成49710千克大麦,也就是不到50吨。 这个麦粒数学问题此后在中东到西方世界都十分流行,古埃及也知道这个问题,因此瑞典数学历史学家约兰·弗里伯格(J?ran Friberg)推测这个故事和棋类游戏结合起来,或许与古埃及掷赛游戏塞尼特有关,因为塞尼特的棋盘有30个方格,不过没有任何证据。 |

|
|
公元前14世纪的塞尼特棋盘 按照当时流行的故事,要掏50吨大麦的话,国王应该还是能拿出来的。 至少,麦粒问题没有被古希腊人代入到棋盘问题上。因为古希腊玩的Petteia棋(类似于西洋双陆棋)目前没有实物,有的说是12X12的棋盘,也有说是8X7棋盘,等等,似乎并没有什么固定棋盘大小,为了方便理解,现代还原时代入到国际象棋棋盘上,才采用8X8的棋盘。所以阿基米德和国王压根没法讨论这个问题,纯属后来人搞得“时代错误”。 |

|
|
阿喀琉斯和埃阿斯下Petteia棋,公元前 540-530 年 已知最早将麦粒问题代入到棋盘上的可能是波斯人。6世纪左右印度人将“恰图兰卡”(古印度象棋)带到了波斯,波斯人改进发明了“沙特兰兹”(波斯象棋),这种象棋和现在的国际象棋的规则已经很接近了。 |

|
|
14世纪的波斯手稿,描述印度人如何将恰图兰卡带至波斯王宫 大概是为了解释这种深受大众欢迎的象棋是怎么发明的,9世纪的阿拉伯历史学家叶耳孤比记录了这样一个故事: 一些印度学者声称,当国王巴尔赫特的女儿朱希尔成为女王(王后?)时,有人发动了叛乱。作为一位聪明的年轻女子,她派了一个儿子去应对——她有四个孩子——但叛军杀害了她的儿子。 这让她的王国的民众感到痛苦,由于不敢告诉她这个消息,他们聚集在一位名叫卡夫兰的智者面前。卡夫兰是一个充满智慧、聪明和判断力的人,民众告诉了卡夫兰事情的经过,卡夫兰说:“给我三天时间。”经过深思熟虑后,卡夫兰对他的一个学生说:“给我找来一个木匠和黑白两色的木头。” 于是学生按照他的吩咐去办了。智者画了一个棋盘,吩咐木匠制作。然后卡夫兰对学生说:“给我拿一张晒过的兽皮来。” 他命令学生在上面画六十四个方格;学生按照他的吩咐画好方格,然后将兽皮放置在棋盘上。智者和他的学生互相对弈,两人熟练掌握了这种游戏。智者对弟子说:“这是一场没有伤亡的战争。” 三天后,民众前来找卡夫兰,于是卡夫兰就把新发明的棋展示给他们看,民众发觉这棋中蕴含着无限的智慧。 朱希尔女王听到了卡夫兰发明新棋的消息,她召见了卡夫兰,并命令他展示他的智慧结晶。卡夫兰拿出棋盘,放在他和学生之间。两人对战,其中一人击败了另一人并大喊道:“将死!” 女王注意并且意识到了卡夫兰想要说什么,她问道:“我的儿子被杀了吗?” “正如您所说的, ”卡夫兰回答道。 女王对她的管家说:“让民众进来,允许他们向我表示哀悼……” 此后,朱希尔询问卡夫兰,如何给予他报酬时,卡夫兰便提出了每个方格上麦粒倍增的报酬方式。 类似的故事还见于《列王记》,有人认为“巴尔赫特”可能是指的印度笈多王朝的旃陀罗·笈多二世(超日王),“朱希尔”可能是指超日王的女儿波罗婆瓦蒂(Prabhavatigupta,?-443年),她嫁给印度中南部的伐卡塔卡王朝鲁陀罗犀那二世,至少摄政了13年。 现在最为流行的版本大概是13世纪阿拉伯历史学家伊本·赫里康等加工的版本,然后随着国际象棋传入西方而被熟知。 |

|
|
巴西艺术家蒂亚戈·克鲁兹 (Thiago Cruz)在2007年绘制的“西萨发明恰图兰卡” 这个版本主角是印度婆罗门西萨(Sissa,Sessa或Sassa),出于某种教育目的,为某位印度国王(根据不同版本,国王名为巴尔赫特(Balhait)、沙赫拉姆(Shahram)或拉达瓦(Ladava))发明了“恰图兰卡”(印度象棋)。 国王十分满意,说要给西萨奖励,西萨便提出了每个方格上麦粒(或者大米粒)倍增的报酬方式,最终经过计算后,国王发现哪怕是用全世界的麦子都无法满足西萨的需求。 因为最早的叶耳孤比讲的故事中没有提到结局,因此最后国王解决问题的方式也是开放性的,不同的叙述者会根据自己的喜好填上不同的结局: 1.因为贪得无厌和欺骗国王,西萨被判处死刑或流放。 2.西萨被惩罚在监狱里数他赚到的麦粒,直到他去世为止。 3.因为全国的财产都没有这么多,所以西萨获得了整个王国。 4.西萨得到了奖励,但他所要求的谷物的价值是用黄金支付的。(当然这也不可能) 5.西萨要求将粮食分发给最需要的人,然后离开了(故事的前提是国内百姓受灾而国王熟视无睹) 6.西萨没有真的要粮食,他说自己只是给国王一个教训:“在您做出任何判断之前,请考虑后果”、“请注意,您的善意很容易被滥用。”西萨因此成为国王的心腹或者获得了王国最高的荣誉称号、或被任命为首相(大维齐尔)。 |

|
|
参考资料: https://history.stackexchange.com/questions/5992/what-is-the-origin-of-the-wheat-and-chessboard-legend?history.stackexchange.com/questions/5992/what-is-the-origin-of-the-wheat-and-chessboard-legend The invention of chess in legend?www.chess.com/blog/introuble2/the-invention-of-chess-in-legend |

|
|
|
|
拖着,交给下一任国王解决 |

|
|
好家伙全是自动删除的评论,你们可别乱说话 |
|
国王把自己的随身宝刀交给阿基米德,让他以此为凭证明天到国库领取自己的米。 然后,大臣告知阿基米德国库的地址,害怕他找不到还画了一张地图。 第二天,阿基米德依约到国库。刚进门还没来的及说话,阿基米德就被卫兵摁倒在地。 阿基米德抬头看去,只见上方挂着一块牌,牌上用希腊文写着“白虎节堂”。 |
|
国王通过拼多多交付,只要阿基米德的砍价进度达到100%就能获得这些米。 |
|
国王:历史文件……不具有现实意义 |
|
为了方便购买大米,国王建立了“米联储”。 “米联储”因为黄金储备不足以购买足够的大米,于是开始印刷大量的“米钞”。 国王宣布“米钞”不再与黄金挂钩。 国家开始使用印刷的“米钞”,从东方某国进口大米。 国内农民抗议进口东方某国的大米导致他们失业。 国王宣布对从东方某国进口的大米加征关税。 国内CPI持续达到10%左右的高位。 为了遏制通货膨胀,“米联储”不断加息。 国内的贵谷银行、千米银行、第一供禾银行纷纷倒闭。 ——阿基米德罪大恶极! |
|
国王算清楚后知道自己的粮食不够,于是邀请阿基米德饮宴,二人大醉。半夜国王起夜,拔刀砍了阿基米德,再安然睡去。 次日醒来,痛苦曰:“孤好梦中杀人,痛哉吾大数学家!厚葬吧。” |
|
国王说,但是这些是我赏赐给你的,所以这些米不能卖不能扔不能送人不能喂牲畜,只能自己家人吃。你吃完第一格我给你第二格,吃完第二格给你第三格,以此类推。阿基米德一看这样国王也没有违规,自己后半生吃饭问题也解决了,还可以给国王一个台阶下,欣然接受,完美解决。 ===========更新========== 这种方法是双方都能接受,同时国王算是履行了承诺留住了面子,阿基米德也得到了好处。人家阿基米德都让步了给你留足了面子,你国王也不要再给人家下狠手了,不要为人家公子吃米,也不要让人家今天必须吃完,那样反而把对方给你留的面子给撕破了。 当然这个故事并不是发生在阿基米德身上,这种细节也不用太在意了,像西方的神话故事,传到我们这里很多都变了主角,因为我们对西方的历史人文了解很少,翻译过来名字都那么长,不熟悉的人想记住都难,只要道理没有偏就好,爱谁谁。 当然还有另一种,就像qq微信转发谁和日本的赌约一样,转发多少次日本就输了,有人说是李连杰,有人说是成龙,还有人说是马化腾,反正不管是谁,都影响不了转发的人的智商 |
|
国王没解决,但是罗马人帮他解决了。 |
|
国王和阿基米德签署协议将大米展期20年,前十年只给米糠不给大米。 |
|
这就不得不提到我大汉棋王汉景帝的智慧了 |
|
国王大喊一声:“原神,启动!” 一瞬间,无数的米wb和米黑就填满了所有的方格。 |
|
国王为阿基米德的智慧而惊叹不已,爽快的愿赌服输,由于米量巨大,为了防止中途有人贪污,国王下令每一个格子的米都必须切实的进到阿基米德及其后人的胃里。 于是在国王偿还了( )格米之后,阿基米德族灭.................... |
|
首先那个故事里不是阿基米德,而是印度的一个臣子,毕竟国际象棋是从印度传到西方的,阿基米德那时候希腊应该还没有 然后据说是国王发现给不了那么多米后就大怒把臣子给杀了,在绝对的权力与暴力面前任何小聪明都是没用的 |
|
分期支付,第一个格子里的米当时支付,第二格两天后支付,第三格四天后支付……以此类推。 |
|
拿出一大袋米,说就是这么多,你不信请你去数吧,什么你数好了,那你数错了,再数一遍。什么你又数了一遍没错,可是我手下4个大臣,8个侍从,16个个仆人都数过了,肯定你数错了。 对了,明天还有一个米仓给你数哦,不数完不给出来的那种。 后天可以把整个地区的粮仓给你数哦,千万要一粒一粒数,这样才准确呀。 |
|
国王:我答应 \neq 我要填 |

|
|
|
|
国王大手一挥就给了呗。三千大千世界都只是自己国家的一个无名氏小村庄而已,这2^64颗米甚至还不到一个地球质量,价值约等于零,居然就能打发走阿基米德,比打发叫花子还容易。 第二年国王得了白血病,病入膏肓,每天躺在床上,连吃饭的力气都没有。请了女娲娘娘来治病。女娲用补天的五彩石做药给国王熬水喝。一个月后,国王的病就完全好了,一口气上九楼,不费劲。国王说要重赏女娲娘娘。救命和赢棋的功劳根本没有可比性,所以让女娲娘娘提一个比阿基米德的要求更大得多的奖励。女娲说我还是只要米,但是换一个规则。 女娲拿出一张纸,写上(0.0)(1.1)(2.2)(3.3)(4.4)(5.5)[5]。她告诉国王,这是一个数字游戏,每走一步,括号里的东西会按一定规则修改和复制。等小括号全部清零后,中括号里面的数就是你要给我的米粒数量。规则是这样的,首先找到比最后一个小括号()的两个数都小的最靠后的括号(4.4),称(4.4)为坏根。用(5.5)减去(4.4),第二个数继续减1,得到x=(1.0)。然后删除最后的(4.4),把坏根和之后的部分(这里只有(4.4))复制5次(中括号里面的数字那么多次)。注意每轮复制时,都要给每个括号里的数字加上x。之后的规则也一样,如果最后小括号里的第二个数是0,就不需要求x,只需要找第一行的坏根并按之前的方法复制中括号里的数字那么多次,第二行对应照抄即可。等最后一个括号变成(0.0)之后,就可以删除这个括号。我们来看看具体情况吧,先来一个小一点的(0.0)(1.1)(2.1)[1]试试? (0.0)(1.1)(2.1)[1] (0.0)(1.1)(2.0)(3.1)[2] (0.0)(1.1)(2.0)(1.0)(2.1)(3.0)(2.0)(3.1)(4.0)[3] 接下来数字太长了,不是很好算了。但我们至少知道,这不会小于单行的(0.1.2.1.2.3.2.3.4)[3],我们继续看看单行的情况?8个数字还是有点多,先看看(0.1.2.3)[3]? (0.1.2.3)[3] (0.1.2.2.2)[4] 0.(1.2.2)×4[5] 0.(1.2.2)×3.(1.2)×5[6] 0.(1.2.2)×3.(1.2)×4.(1)×6[7] (0.(1.2.2)×3.(1.2)×4.(1)×5)×7[8] 继续写下去会很长,但我们可以看出来一个规律,这些项和序数之间貌似可以对应起来,类似于HH的思想。所以先用序数分析一下。 0~1 0.0~2 0.0.0~3 0.1~ω 0.1.0.1~ω×2 0.1.1~ω2 0.1.1.0.1~ω2+ω 0.1.1.0.1.1~ω2×2 0.1.1.1~ω3 0.1.2~ω^ω 0.1.2.0.1.2~ω^ω×2 0.1.2.1~ω^(ω+1) 0.1.2.1.1~ω^(ω+2) 0.1.2.1.2~ω^(ω×2) 0.1.2.2~ω^ω^2 0.1.2.2.2~ω^ω^3 0.1.2.3~ω^ω^ω 0.1.2.3.4~ω^ω^ω^ω 0.1.2.3.4.5......~ε? 由此可见,(0.1.2.3)[3]≈Hω^ω^ω(3)=fω3(3)。这已经比烂大街的葛立恒数和康威链表示的数字要大很多。单行表示法的上限可以达到Hε?≈fε?,和古德斯坦数列的增长率差不多。 再来看看双行表示法?还是从最简单的开始,慢慢来。 (0.0)(1.1) =(0.0)(1.0)(2.0)...... =(0.1.2.3.......)~ε? (0.0)(1.1)(0.0)(1.1)~ε?×2 (0.0)(1.1)(1.0) =(0.0)(1.1)(0.0)(1.1)......~ε?×ω (0.0)(1.1)(1.0)(1.0)~ε?×ω2 (0.0)(1.1)(1.0)(2.0)~ε?×ω^ω (0.0)(1.1)(1.0)(2.1)~ε?2 (0.0)(1.1)(1.0)(2.1)(2.0)(3.1)~ε?3 (0.0)(1.1)(1.1) =(0.0)(1.1)(1.0)(2.1)(2.0)(3.1)......~ε?^ω (0.0)(1.1)(1.1)(1.0)(2.1)(2.1)~ε?^ω2 (0.0)(1.1)(1.1)(1.1)~ε?^ω^ω (0.0)(1.1)(2.0)~ε?^ε? (0.0)(1.1)(2.0)(1.0)(2.1)(3.0)~ε?^(ε?×2) (0.0)(1.1)(2.0)(1.1)~ε?^(ε?×ω) (0.0)(1.1)(2.0)(1.1)(1.0)(2.1)(3.0)(2.1) ~ε?^(ε?2×ω) (0.0)(1.1)(2.0)(1.1)(1.1)~ε?^ε?^ω (0.0)(1.1)(2.0)(1.1)(2.0)~ε?^ε?^ω^ω 后面还没来得及分析,有空再来补上。 国王仔细观察和分析了很久,才发现自己被女娲坑死了。自己需要给女娲的米粒数量至少远大于fε?^ε?(5)。什么三千大千世界,拿实物的思维去和可计算性理论造出来的,根本谈不上正常读写的大数来攀比,比蚍蜉撼树还要可笑。 最后女娲娘娘说免除国王这笔数额无法描述的巨债,条件是国王把位置让给我,把皇室里上下九代人的全部财富送给我。如果国王你不干的话,我既然能治好你的白血病,也能让你再得一种更重的不治之症。国王听了很绝望,但为了保命,只好照办了。女娲娘娘坐上了王室宝座,国王和皇室的人全部穷得流浪街头。 这真是一个悲剧啊!国王低估了大数函数的力量。 |
|
这怎么又变成阿基米德了? 老外就那么喜欢见缝插针的往你那古希腊“祖宗”脸上贴金吗? 且不说阿基米德那时候有没有象棋,我记得这故事一开始是伊斯兰教的吧? 非要回答的话,建议让莎士比亚来治治这群耍小聪明的数学家。 具体点说参考《威尼斯商人》,让他自己数麦粒去,一颗不能多,一颗不能少,而且不能有任何一粒超出格子。 |
|
|
| [收藏本文] 【下载本文】 |
| 时尚穿搭 最新文章 |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |