[自然科学] 给高斯一个小时，他能否破解三阶魔方？

天天财汇购物网址万年历小说 | 三峰软件小游戏视频

TxT小说阅读器
↓小说语音阅读,小说下载↓

一键清除系统垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

图片自动播放器
↓图片自动播放,产品展示↓

首页淘股吧股票涨跌实时统计涨停板选股股票入门股票书籍股票问答分时图选股跌停板选股 K线图选股成交量选股 [平安银行]

股市论谈均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

商业财经科技知识汽车百科工程技术自然科学家居生活设计艺术财经视频游戏--

天天财汇 -> 自然科学 -> 给高斯一个小时，他能否破解三阶魔方？ -> 正文阅读

[自然科学]给高斯一个小时，他能否破解三阶魔方？

[收藏本文] 【下载本文】

给高斯一个小时，他能否破解三阶魔方？
关注问题?写回答
[img_log]
数学
卡尔·高斯（Carl Gause）
魔方
给高斯一个小时，他能否破解三阶魔方？

高斯盯着魔方，于是魔方的每一个方块自发复原。

顶级数学家证明魔方是可以解决的，然后去做其他事情了
姓费的数学家号称魔方20步就能解决，而且找到了一种美妙的证明方法，但是信里空间太小写不下
高级数学家R给出了一个上限，魔方可以用100,000步解决
普通数学家A改进了这个上限，证明可以用至多1,000步解决
顶级魔方爱好者B发明了人类用来还原魔方的一整套公式。相比于数学问题，这更像个工程问题
普通魔方爱好者C可以在1分钟内还原魔方。未经系统学习的普通人别说一分钟以内了，拼好一面都够呛
高级魔方爱好者D可以做到10秒钟内还原魔方。称得上不可思议，百里挑一。耐心、天赋、努力缺一不可。
顶级魔方爱好者E可以做到3.47秒还原魔方。这是目前的最高水平
高级数学家T证明了魔方可以用至多20步解决，还证明了20是这个问题的下限。
关于魔方还有许多有趣的问题，比如盲拧、脚拧、镜面魔方等等。但是三阶魔方最重要的问题已经被这些人搞定了。
接下来会有人把三阶魔方推广到四阶五阶乃至N阶，给魔方加上种种限制，变成五魔方、四面体……
另外，在真实历史中，对魔方贡献最大的数学家恐怕是从来没有见过魔方的伽罗瓦

第一天，Gauss先证明了三阶魔方的上帝之数是20，他看20是不好的。于是第二天，祂证明了三阶魔方的Gaussian数是19。事就这样成了。

一个被打乱的魔方一定可以被还原是显然的。
如何鉴别一个魔方不是打乱而是胡乱拼接的，所以无法还原，这个可能需要花上几分钟。嗯，最多几分钟。
然后问题就被解决了，至于魔方，砸了重新拼好就好了……

破解魔方，是个工程学问题；
而高斯，是个数学家。
数学家的逻辑一般是这样的：他们会用几秒钟的直觉得出这个魔方是可以复原的，然后用可能几分钟到几十分钟给出对这个结论的证明，大概率会给出一种从一个状态拧到一个相邻状态的方法，以及按此步骤循环回初态的一个类似于G(64)这样的步骤数上界；
然后这个“数学问题”就已经被解决了。
至于把它真的拧回去这种纯体力工作…请不要拿这种事来侮辱处于学科鄙视链最顶端的数学家好吗

第一秒钟，高斯穷举了魔方所有的变化，选择了步数最少的方式还原了。

前提是完整的可还原的三阶魔方。
接下来我说明一下一个数学角度解魔方的简单方法。
这是三个圆

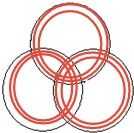
这是三个有三个圆的同心圆

每一个同心圆的一个大交点我们定为9个，两个大交点就是18个，三个就是27个，四个就是36个。算重叠，每个总共有36个交点。
这三个同心圆总共54个交点。
其中九个交点可以等效为魔方的其中一个面。这六组交点就可以等效为魔方六个面。
转动其中一个同心圆的圆圈使交点值前进到下一个大交点，等效为魔方其中一层转动。
因为一个同心圆有四个大交点，可见，转动一个小圈则影响四个组合值的变化，并使转动的圆圈的值往前进一，退出第四个大交点的值，重新进入第一个大交点的值。
这样，我们就成功把魔方问题转化为平面几何问题进行解答。
接下来我们只要对这些同心圆构成的二维图形的所有交点进行代数运算。
很容易就可以得到魔方基本公式，比如不影响某一种情况下实现这个色块到另一个地方的公式、不影响两个面把这几个色块翻棱等等的公式。
有了这些公式就可以进行还原魔方了，剩下的就是训练公式的熟练度，这就不在讨论范畴了。
所以......你觉得高斯会想不到这种方法吗？

高斯看见了魔方，他思考了一下，不是思考如何还原魔方，而是已经完成了关于n维空间下m阶魔方最少还原次数的论文。

很多人都搞错方向了，要回答这个问题，那就要反过来说揣摩题主为什么要提这么个问题。
逻辑是这样的，提问者认为大家大概率会说高斯无法在一个小时内破解三阶魔方，然后就开始嘲讽一波高斯/数学家。
你要问我为什么，因为我作为一个数学博士也是经常被人这样搞过，回答出了不能证明水平多高，回答不出更加尴尬。
当然我人是比较好，还是愿意去接这种坑，但是我还是要说，建议把此类用来侮辱高斯以及各数学家的提问者好好地送去北大数院深造一番，让他们自己亲自体会当傻子的感觉，以后就不会提这种问题了。
人与人之间的可怕之处不是差距有多大，而是根本不知道自己和别人差距有多大。

高斯盯了魔方3秒钟，决定在三维空间中引入一个卷曲维度，于是三阶魔方变得不可解。高斯感到这是好的，于是就休息了。第七天，高斯感到无聊，就随手移除了这一卷曲维度，于是三阶魔方重新可解。之后高斯就忘记了这一事，这是第八天。

这个问题我了解。研究生毕业最后一段时间，没啥事做，和一个同学打赌，看谁在“不借助任何外力”的情况下解出魔方。
从二阶到四阶第一次解出，大概用了两个多月。（当然，期间也不是专心解，还是闲下来才搞得）。总共的时间不太长，所以，我觉得以高斯的聪明才智和数学基础，一个小时只解三阶，估计差不多，但是不是最简方法不一定。
下面简单介绍一下我的解答过程。
我是从二阶开始解的，开始有两个思路
一个是“寻找实现某种状态的操作（比如研究如何对换相邻的两块而不引起其它变化）”
一个是“固定某种操作寻找不同的叠加状态（比如右上上左右下上右右下，观察这个操作后哪些块发生了什么变化”）
我估计正确的玩儿法应该是第一种，但我当时没搞出来，所以采取了第二种思路。
然后就是建立基本模型。二阶的还好，每个块有八个位置点，三个状态量。然后设计一个矩阵运算，就能基本确定什么样的状态存在，什么样的不存在。（但是后来发现这个数学模型对我帮助不是特别大）
到三阶魔方，模型又多出了一个中间位置的两种状态，一下子变得非常复杂。
定义好基本设置和解题思路后，我很快就找到了二阶魔方的解法。虽然复杂一些，但是能解出来。
然后将同样的解法推广到三阶。在三阶中又添加了一种操作来调整边位置的块。这样用角位置和边位置不同的循环数去拼出来我要的状态（我记得我的角变化是6次操作一个循环，边是三次，这样就可以利用它们的周期去寻找不同的边角状态）。于是，三阶的也解决了，当时我同学就在旁边，他都惊呆了哈哈。
然而，实际上我三阶的没有完全解出，按照我的方法到最后会有一种情况是不对的。感觉是我少定义了一个隐藏态导致的，可惜到最后我也没找到问题所在。所以，其实我拼三阶魔方是概率性的，拼完不行我就打乱再来一次，一般就可以了。
四阶魔方我是按照中间两块是整体，简化为三阶去做的，最中间的位置是一个二阶魔方。同样的，三阶魔方的问题依旧存在。还多了一个四阶特有的问题（中间两块状态相反）。最后努力了很久，也只拼出来两次四阶魔方。
我添加了一个四阶特有的中间两块的“旋转值（只有正负）”，然后发现有一些操作会改变整个魔方的旋转值（类似于逆序数），这种操作必须是偶数次。算是勉强解决了这个问题吧。
开心的是，打赌赢了一顿大餐，哈哈。

一小时后，高斯：20
魔方：对，他说的对。

考虑到三阶魔方总的状态数小于一个小时内的普朗克时间数量，这件事只需要速度够快就一定能实现，哪怕是没有所谓智慧的扫地机器人。但高斯肯定不行，人的反应速度很慢，比如万分之一秒的时间谁也感受不到。

高斯写出了一个O(1/n)的解法。

高斯会先解决n阶魔方问题，然后让n=3

一个小时可能不会，但很大可能会搞出一套理论。
高斯传第一部分 - 哥廷根数学学派的文章 - 知乎https://zhuanlan.zhihu.com/p/54
高斯传第二部分 -哥廷根数学学派的文章 - 知乎https://zhuanlan.zhihu.com/p/54

高斯认为三阶魔方没有意义，于是这个概念在世界上消失了。

不需要高斯，也不需要一个小时，你其实可以去问问身边玩异形魔方的人。普通人就可以在一个小时内破解比三阶更复杂的魔方。

这是大学时候的部分存货，那个时候刚开始玩异形，图片中的pattern都是我用自己的解法拧的，当然这些并不是什么复杂的pattern
我自己买过的异形魔方少说也有20多30个了，其中绝大部分刚到手的时候，对我来说都是全新的，从来没见过的魔方。我的所有魔方，除了两个Oskar大神授权量产的异形，剩下的我全都找到了通解。除了三阶魔方是我很小的时候我朋友教会的，我至今都没有上网看过任何所谓的还原教程。
除了最早开始玩的3，4个异形魔方，因为经验不足花的时间比较久，找到解法花了几个小时到几天不等。后面买来的绝大多数难度中等的异形魔方，都能在一个小时甚至半个小时内还原。

这是我现在身边的一部分魔方，还有很多送朋友了
后来才知道网上有很多异形魔方爱好者，像我一样专门以破解异形魔方为乐趣。我玩过的魔方和他们比简直是小巫见大巫。甚至还有许多没法在三维空间中造出来，但可以在电脑上玩的魔方。
要想自己破解魔方，说简单其实也不算很简单，偶尔还是会把自己给难住的，比如如果买到的是某类会影响旋转自由度的Jumbling魔方，或者不具有群结构的魔方，通常卡住会很难推进下去。

高斯能否仅用一个小时独立破解三阶魔方？不排除这种可能。
(根据读者的反馈,文末新增五)
一
破解魔方，注意我这里指的是一个小时内独立找到复原方法，假设高斯是当时世界上第一个复原魔方的人，没有其他人的成功案例可以参考学习。据说魔方的发明人鲁比克教授花了一个月时间独立破解。当然他不可能每天花费全部时间在破解魔方上。这个问题有挑战性，但只要解决方法论问题，后面的就是试错，纠正，再试错的过程。只要高斯能找到解决问题的正确思路，他就能快速整理出世界第一份魔方复原方案。
下面我就把我想到的一种如何寻求破解的思路讲述一遍，整个过程只需要小学的数学知识。所以，以高斯能在小学课堂上提出快速解决前一百个自然数之和的能力，即使他是年幼的小学生，也应有能力想到我下面这个思路。再强调一下，下面的思路的理解只需要小学的数学知识，如果我用到哪个超出小学数学的术语，你只要替换成术语后括号中的通俗说法，不影响你的理解。如果这篇文章引起你的兴趣，你可以参考这些术语找到相关书籍深入学习。
如果下面你觉得看不太懂，那可能是你没仔细观察过魔方，又没有魔方实物在身边，仅凭空中想象感到吃力。如果你不熟悉魔方，手边最好准备个真正的魔方或下载个魔方APP，后面阅读时更容易跟上思路。
二
现代计算机解决难题经常用“分而治之”的策略。“分而治之”的办法并不是现代科学家的发明。古代比较典型的例子就是张仪的连横术。秦国想要一下子消灭六国，不容易。但秦可以化解六国联盟的势头，保证每次攻打某国时，其它国家不帮着抵抗。
这样秦国从容易下手的国家开始，一步步，把难以吞并的六国，逐步蚕食，最终解决。计算机采用同样的策略不是争天下，而是解决难题。
具体到魔方。看似难，先把问题分析，然后分解成容易的步骤。从容易的部分开始，最后完成复原。
魔方一共六个面，每个面九块颜色，9*6=54 带颜色的正方形。
再仔细观察，虽然有54正方形颜色面，真正的立方体块数只有26块。因为魔方一共三层，每层9块。9*3=27块。但是最中心的块你是无法操弄的轮轴枢纽，这一块，你的眼靖也看不到。所以去掉这个块，剩下26块。
1）其中魔方每个面中间的色块特殊，只有一个面朝外。并且永在中心，是比较固定的部分。并且最顶层的中间颜色是与最底层中间颜色是固定对应的。注意下面我说的是标准魔方颜色方案，比如最顶层是白色，那么最底层就是黄色，如果你买的是不标准的魔方，白色未必对应黄色，那也没关系，原理是一样的。所以解决魔方时，以比较固定、容易的各个面的中心为基础。
这类立方块有6块。
2）排除第一种情况的6 块，26-6=20，剩下的20块中，永远在各个顶角的有8块，每块三面颜色。
3）排除1）2）6块和8块，26-6-8=12，最后还剩 12块，永远在各个棱/边的中间，每块两面颜色。
分析后，拿着魔方，最简单的想法，先完成魔方一面。
但是经过上面1），2），3）的分类整理，你也应该意识到每个魔方面的中心块也是容易的部分，然后是楞上的中心块。所以底面，想到先弄成个“十字”的想法顺理成章。同时，一旦底面的中心定下来，比如是白色，那么顶层的颜色必定是黄色。所以在底面形成白色十字的同时，你会想到其他各个面的中心也应该定下来。这样一旦底面的白色完成实际第一层的中间色块和第二层的中间色块也应该随之相应完成。有了这个思路，尝试多次就能完成底面全白色，第一层和第二层的中间色对好，这一部分比较容易，方向对头，只要胡乱试都能成功。
现在逐层完成的思路已经呼之欲出。底面白色完成，第一层完成，第二层只差四个角块。还是直觉的考虑：要找到一个方法，或者一系列操作，在不打破已完成的底面全白色和第一层、第二层的中间色的情况下，把第二层的四个角块对好。
三
群论（**东西）完整体系的正式建立，要等到高斯死后才完成。但这并不妨碍高斯在摆弄魔方时，凭数学家的直觉，快速发现并使用群论（**东西）的思想。你看了我下面的具体例子分析，你会明白，你可能不熟悉群论（**东西）这个术语，但不妨碍你发现其朴素的思想并且应用在魔方上。我再重复一遍不要被群论(**东西)这名头吓跑，以下依然小学水平即可。
1）如果我们用字母 A 代表一系列操作，那么字母 A' 代表 A操作的逆向操作。E 代表魔方未发生A变化的状态，那么先对魔方进行一系列叫做 A 的操作，再原路返回进行A'操作，一步一步退回去，直到恢复原来状态E，整个流程下来，就是 AA' = E 。比如把魔方某一个面顺时针旋转90度是A操作，再逆时针旋转90度是A'操作，那把这两个操作完成后，魔方又回到没有顺时针旋转90度的状态。即使没有线性代数(**东西）的知识，你可以理解为，A为某个具体的数字比如8，A'为 1/8
AA' = 8乘以1/8 = 1，1 代表原始状态。
2）那么不用逆操作，能否回到操作前状态？
可以，一个操作，比如旋转九十度，你只要重复这个操作，重复四次，你会发现魔方恢复到未做操作前的样子。用字母表示， AAAA = E，以高斯智力，他能很快进一步意识到更复杂的操作：一个操作包括很多个旋转，也是如此。只要重复同一个复杂的、包含很多步骤的操作，重复多次也可回复到原来状态。
3）通过以上分析，高斯会非常自信地找到一个办法把第二层的一个楞上的块对好，其他三个楞上的块用同样办法即可。并且在底面白色，第一层已完成的情况下，剩下的状态有限，更方便寻找处理剩下的角块和中间色块的方法。
要寻找这个解决办法时，他可以用1）操作、逆操作的思路尝试，如果出错，逆操作还原。如果不顺利，他还可以用2）重复操作,回复原状态的方法。他只要记住自己的操作是什么，一直重复同个操作直到回复原状。第三层也是同样思路，找到反转这层中间色和交换四个角的算法（办法）。
当到第二层，特别是到了顶层/第三层，已接近胜利，但面对的危险更大。因为一不小心就会把底下二层搞乱。可在探索过程中，也有好消息。
如果你尝试翻转顶层某一个色块，顶层其他部分不动，也确实做到了，可是你发现只考虑顶层，下面的两层却被搞乱。已有的工作被摧毁。这时按理应该做逆操作回复原状。但你也应该注意到，刚才的操作虽然让下面两层乱了，但顶层的所有色块没有和下面两层发生任何交换。如果这时，你大胆地只旋转顶层，90度或更多，然后再实行逆操作，你应该预测到，下面两层会回复到已完成的状态，但第三层却和操作前不同。这不是恰好你想要的么？因为第三层没完成，并不完美，你需要第三层发生变化，而下面两层不变。通过这方式，到了第三层也不会影响破解魔方的速度。
另外，假设寻找到某个算法B（办法B）后，他发现某一个色块与B的要求不符合，他可用一系列操作C把这个色块调整与B的要求相符合,完成B操作后,然后再用C的逆向操作C'将其他色块恢复原状。用字母代表更简洁：
CBC'
以上在群论里被称为共轭（先搭建条件满足要求，完成后再清理搭建的条件）
四
最后，要注意数学高手在试错的过程中，更清楚自己的操作在干什么，寻找算法（办法）会少浪费时间。我们知道各领域高手的复盘能力都很强。比如说围棋高手下完棋后，可以凭记忆，把整个棋盘复原。国际象棋也是如此。
那么数学家呢？
数学家欧拉晚年双目失明，只凭大脑就能推导极为复杂抽象的数学理论，并且发表论文。欧拉是史上发表论文数第二多的数学家，他有近一半的著作是失明后完成的。其记忆力和心算力惊人。有的人认为高斯比欧拉的贡献更大，毕竟有数学王子的称号。所以高斯凭借大脑复原魔方的能力也不会差，他运用以上的思路，找到破解魔方的办法时会比普通人更快。
五
题外话，如果你能跟着我的思路大致走下来。你会发现整个过程由起初的全局策略，接着细化问题，从易到难，渐入佳境。这时却发现高处不胜寒，步履维艰，接着一不小心就跌入险境。但当你以为就此失败，定心揣摩却迎来柳暗花明。如此忽高忽低，终于攀爬上胜利的顶点，一览众山小。
你如果不喜欢数学，甚至厌恶数学，可借此机会体验一下数学解题的精神冒险之旅。为什么那么多人喜欢数学，甚至以此为职业，是因为有家长，老师、老板的逼迫么？还是金钱、权力、美色的诱惑？这些外在驱动不能说一点都不起作用。但最根本的原因是数学问题本身就散发迷人的魅力。有的人痴迷于数学题时，甚至把命都放在了第二位。罗马士兵闯进屋里要杀死阿基米德，他唯一的请求是别破坏地上的圆，让他做完这道题再杀他。
数学为这么有这么大魅力？
你玩过游戏，像密室逃脱，为什么乐此不疲。因为你知道解困脱生的线索就在这间房里，只要耐下性子找，就能一步一步寻到钥匙，脱离危险。一道数学题堪比一个脱困游戏。但数学题更简洁、更优雅。你知道解这个问题的钥匙就在问题的短短几句话里。但要脱困却要花费更多心思，挑战更大，当然成就感就更强。

世界上第一个还原魔方的人，就是他的发明者鲁比克，用了一个月时间。
魔方还原实际上就是找规律，算出公式，而鲁比克教授是一个建筑学家，并不是数学家。
四色定理对高斯而言，竟然简单到略过，魔方的还原公式更是不在话下了，一个小时感觉都用不了。

高斯还和你玩345呢？直接搞个n阶，以后这个问题就消失了

一个小时行不行不好说，但是给够时间他可能会琢磨出一套群论的理论出来，然后再用抽象的数学对这玩意进行降维打击。

我们初中校庆时就有同学在台下观众席把这东西给弄明白了。
两小时的大会，搞懂一个三阶魔方前后不到一小时。剩下的时间就是在各种胡乱摆弄再快速还原。
我是不相信高斯会比我的校友差。

爆肝9800+字，本文共计收录常用非标F2L：53个CASE，提供119种解法，其中包含部分CASE的双向或者四向解法，整理总结实属不易，且还配上了相应的动图与分析来让读者更好地理解并掌握非标F2L后，运用到自己实际还原中，以达到提高自己水平的目的。图片版可自行下载，在文末。
故，建议收藏学习，再点个赞，你的支持是我进一步分享的动力，点个关注更是对我最大的支持！~
引言：
道可道，非常道；名可名，非常名。
前情提要：
在学习本攻略之前，请至少先掌握标准状态下的F2L，也就是通常CFOP中所说的41个F2L。
如果未完全掌握，或者掌握较浅，请移步：
三阶魔方还原之CFOP-F2L从入门到精通 - 知乎 (zhihu.com)
如不然，纯粹浪费精力与时间，不是特别建议。
基本说明：
本教程采用国际三阶魔方标准配色状态下的魔方作为演示，并以白为底层(D层)，黄为顶层(U层)，且均以白红棱块与白红蓝角块为目标棱块与目标角块进行求解与手法的优化。
非标F2L的定义与意义：
非标F2L即非标准状态下的F2L-相对于41个标准状态下的F2L的异类-也就是说只要不是41标态情况下的F2L我们都可以把其称之为非标。
以最常见的标态F2L03为例：

F2L03
U'后可得：

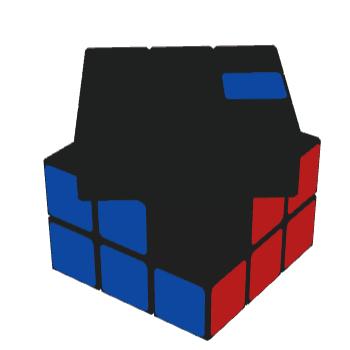
如上图所示，这样的情况就可以称之为非标F2L。
那么，我们如何来完成这一组非标F2L呢？
A、转化为标准状态下的F2L后进行处理，如下：
U(R'F'RU) (RU'R'F)

B、直接使用非标F2L的方法来进行处理，如下：
(R'FRF')(RUR')

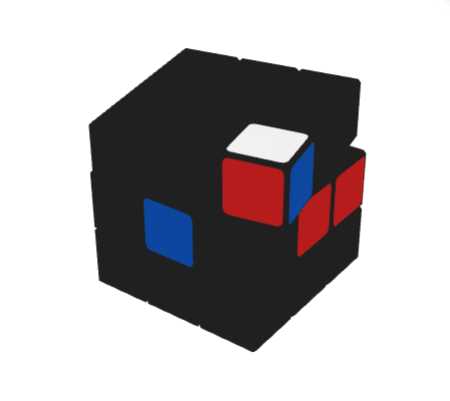
对比A与B两者，可以明显看出，直接运用非标F2L的解法来进行处理-情况B，步数上优于情况A-转化为标准状态下的F2L后进行处理，且顺手程序也不差。
综上，我们也可以得出这样的结论：针对非标F2L，有两种处理方式，
A-转化为标准状态的F2L进行处理；
B-直接运用非标F2L进行处理；
大多数初学F2L的朋友，基本都采用转化为标准F2L进行解决，或者遇到其他一些情况无法转化为标准状态下的F2L后进行处理，或者转换过程极为麻烦，这就大大增加了还原所需的时间。因为想要更快地还原魔方不外乎三点：
1、更少的步数；
2、更快的手速；
3、更少的停顿。
总结与应用：棱块在错误的槽位，角块底色朝上：
情况A：
U' R' U R2 U' R'

总结：角块与棱块直接通过U层转动后形成正确的CE(C-Corner-角块，E-Edge-棱块)组合之后，插入正确的槽位；
情况A'-为情况A镜像，镜像情况均加'表示，下同：
y U L U' L2' U L -亦可作四向手法

总结：镜像情况带魔方整体转动后更顺手；
情况A与A'观察要点:角块白向上，棱块在邻槽且色与邻中心相连接。
情况B：
U2 (R' U R) U' (S R S')
y R' F R2 U' R' U2 F' -可作四向手法
y2 U2 (L F' L' F) (L U L') -可作四向手法

总结：角块远离后，运作棱块后，用中层转动形成组合后插入；手法上前后层夹层S与S'需多练；
情况B'：
y U2 (L U' L') U (S' L' S) -可作四向手法
L F' L2' U L U2' F
y' U2 (R' F R F') (R' U' R)-可作四向手法

总结：B的镜像，上同，手法更顺；
情况B与B'观察要点：角块白向上，棱块在邻槽且色与邻中心不相连。
情况C：
U2 L2' u L2 u' L2'
y U2 R2 u' R2' u R2 -可作四向手法
y' U2 L2' u' L2 u L2' -可作四向手法
y2 U2 R2 u R2' u' R2-可作四向手法

总结：动作角块下底后，能过u的转动直接组合后放回，解得很妙；
情况C观察小结：角块白向上，棱块在对立槽位，且棱块与两相邻中心色为对立色(蓝对绿，红对橙)；
情况C'：
L F' U F L'
y R' F U' F' R -可作四向手法
y' (L' u' L) U' (L' u L) -可作四向手法
y2 (R u R') U (R u' R')-可作四向手法

总结：已形成正确的CE组合，先L把目标槽位放到顶层后把CE放入即可；
情况C'观察小结：角块白向上，棱块在对立槽位，且棱块与两相邻中心色为相邻色(蓝邻橙，红邻绿)；
棱块在错误的槽位，角块底色朝向侧面：
情况D：
R' U' R2 U R'

总结：转换为标态F2L的同时，直接R2UR'解决。
情况D'：
y L U L2' U' L -亦可作四向手法

总结：D的镜像，同上。
情况E：
F D R D' F'
y R (F U F') R'-可作四向手法
y2 F (L U L') F' -可作四向手法
y' R u R u' R'-可作四向手法

总结：角块直接下底，利用了棱块所在槽位作空SLOT通过底层来处理。
情况E'：
y F' D' L' D F -可作四向手法
L' (F' U' F) L
y' F' (R' U' R) F -可作四向手法
y2 L' u' L' u L -可作四向手法

总结：E情况镜像，直接放到顶层来解决，化为非常简单的标态F2L后，L回溯。
情况F：
U' (L' U' L) (R U' R')
y U2 L' U' L2 U L2' U' L-可作四向手法

总结：U调整角块位置，L'后直接组成正确位置的CE，U'后利用L的回溯直接完成CE后插入；
情况F'：
U B U B' F' U F-更顺手解：y U (R U R') (L' U L)
y' U2' L U L2' R' U R L-可作四向手法

总结：镜像解法，分析同上。
情况G：
(F U2 F') (R U R')
y L U2 L' F U F' -可作四向手法
y' R U2 R' f R f' -可作四向手法

总结：藏角后，转换成简单F2L处理。
情况G'：
y (F' U2 F) (L' U' L) -可作四向手法
R' U2 R F' U' F
y2 L' U2 L f' L' f -可作四向手法

总结：镜像解法，同上。
情况D/E/F/G及其相应镜像D'/E'/F'/G'观察小结：首先判断棱块是否与邻中心色相连，然后判断角块朝向(非朝上)；
情况H：
U (R U R') (L U L')
U' (R U2 R') U' (L U L')
y U (L' U L) (R' U R) -可作四向手法

总结：U (R U R') 转化为标态F2L后处理。
情况H'：
y U' (L' U' L) (R' U' R) -可作四向手法
y U (L' U2 L) U (R' U' R) -可作四向手法
U' (R U' R') (L U' L')

总结：镜像情况，藏角后直接组合后插入。
情况I：
U2 F' (L U L') F
y U2 L' (B U B') L -可作四向手法
y' U2 R' (F U F') R -可作四向手法
y2 f' U L U' f -可作四向手法

总结：直接转化为简单F2L，处理后，F回溯。
情况I'：
y U2' F (R' U' R) F' -可作四向手法
U2' R (B' U' B) R'
y2 U2' L (F' U' F) L' -可作四向手法
y' f U' R' U f' -可作四向手法

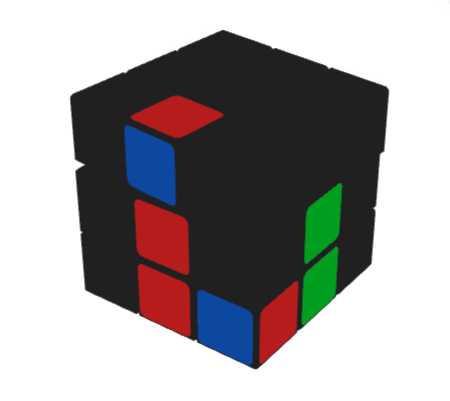
总结：镜像解法，同上。
情况H/I及其相应镜像H'/I'观察小结：先看棱块与相邻中心是否色对立，再看角块白朝向(非朝上)；
角块在错误的槽位-右槽：
情况J：
U (R U' R') (L' U L)

总结：直接用标态方法解法，组合后插入。
情况J'：
y (L' U2 L) U' (L U L')
y U2 (L' U L) U' (L U2 L') -可作四向手法

总结：藏棱后转化为标准F2L解决。
情况J及J'观察小结：角块色白向下，看棱块是否与中心色相连。
情况K：
U2 (R U' R') U (L' U' L)
y (F' L F L') U' (L U2 L')-可作四向手法

总结：U2把棱块调整到合适位置，假藏棱后与棱块组成简单标态F2L处理。
情况K'：
y U' L' U' L2 U2 L'

总结：直接把CE进行组合后避让，后直接插入即可。
情况K及K'观察小结：角块色白朝前(F)，看棱块是否与中心色相连。
情况L：
(R U R') U' (L' U L)
y (S' L S) -可作四向手法

总结：直接组合后插入。
情况L'：
U' (R U R') (F U F')
y U (L' U L) U (L U L') -可作四向手法
y U' (F U F') (L U L')-可作四向手法

总结：藏棱后转化为简单F2L处理。
情况L及L'观察小结：角块色白朝右(R)，看棱块是否与中心色相连。
角块在错误的槽位-左槽：
情况M：
y U' (L' U L) (R U' R')

总结：直接用标准F2L处理后插入。
情况M'：
(R U2 R') U (R' U' R)
U2 (R U' R') U (R' U2 R)-可作四向手法

总结：藏棱后U2即可转为简单标态F2L进行处理；
情况M及M'观察小结：角块色白朝下(D)，看棱块是否与中心色相连。
情况N：
(F R' F' R) U (R' U2 R)
y U2 (L' U L) U' (R U R')-可作四向手法

总结：反向藏角及反向藏棱后组合好后插入目标位。
情况N'：
U R U R2' U2 R

总结：直接组合后插入，注意回溯的先后顺序。
情况N及N'观察小结：角块色白朝右(R)，看棱块是否与中心色相连。
情况O：
(S R' S') -不建议使用
y (L' U' L) U (R U' R')

总结：直接组合后插入。
情况O'：
U (F' U' F) (R' U' R)
U' (R U' R') U' (R' U R)
y U (L' U' L) (F' U' F)-可作四向手法

总结：藏棱后转化为简单标准F2L进行处理。
情况O及O'观察小结：角块色白朝前(F)，看棱块是否与中心色相连。
角块在错误的槽位-对立槽：
情况P：
U' (F' U F) (L U2 L')
y U' (L' U L) U' (f R' f')-可作四向手法

总结：直接按标态F2L进行处理后插入。
情况P'：
U (R U' R') U (f' L f)
y U (F U' F') (R' U2 R) -可作四向手法

总结：直接按标态来解决后插入，注意插入方法。
情况P及P'观察小结：角块色白朝底(D)，棱块与角块色相同在F或者R面，后按标态解决后插入。
情况Q：
(R U' R') (L U2 L')
y (L' U' L) (f R' f') -可作四向手法

情况Q'：
(R U R') (f' L f)
y (L' U L) (R' U2 R) -可作四向手法

总结：直接组合后插入。
情况Q及Q'观察小结：角块色白朝向侧面，非色白面，棱块角与角块色相异。
情况R：
(R U R') U (L U L')
y (L F' L' F) (R' U2 R) -可作四向手法

情况R'：
(R' F R F') (L U2 L')
y (L' U' L) U' (R' U' R)-可作四向手法

总结：逆藏角与棱后插入。
情况R及R'观察小结：建议与情况Q及Q'对应进行观察总结。
角块已还原，棱块在其他槽：
情况S：
R2 U' R2' U R2
y2 L2' U' L2 U L2' -可作四向手法
y F' R' F2 R F-可作四向手法

总结：把CROSS与C进行避让，后与棱块组合后回归。
情况S'：
f' R' U R f
y R' u' R u R -可作四向手法
y' L' u' L u L -可作四向手法
y2 f' D' L D f-可作四向手法

总结:把CROSS与C及棱块同时放置到R层后，先调整棱块位置，CROSS与C再归位即可。
情况T：
y L2' U L2 U' L2' -可作四向手法
y' R2 U R2' U' R2 -可作四向手法
F L F2' L' F'

总结：把C与CROSS相关的E进行躲藏后，先处理要还原的E后，把CROSS和C归位。
情况T'：
y f L U' L' f' -可作四向手法
L u L' u' L'
y2 R u R' u' R' -可作四向手法
y' f D R' D' f' -可作四向手法

总结：利用FL的空槽进行解决。
情况S/T及其对应镜像S'/T'观察小结：角块均已还原，看棱块色与中心是否相连来判断，四个一起组合记忆与区分。
情况U：
L2' u' L2 u L2'
y' R2 u R2' u' R2 -可作四向手法
y L2' u L2 u' L2' -可作四向手法
y2 R2 u' R2' u R2-可作四向手法

总结：利用空槽把棱块还原后，归位受影响的CROSS的E。
情况U'：
(L' u' L) U (L' u L)
y' (R u R') U' (R u' R') -可作四向手法
y (L u L') U' (L u' L') -可作四向手法
y2 (R' u' R) U (R' u R)-可作四向手法

总结：同上。
情况U及U'观察小结：角块均已还原，看F面，目标棱块色与中心是否是对立色；
角块与棱块形成正确的CE组合，但是在其他槽：
情况V：
R' F R2 U' R2' F' R
L F' L2' U' L2 F L'
y (f' L' f) U' (L' U L) -可作四向手法
y' (R U R') U' (f R' f') -可作四向手法
y2 (f R f') (L U2 L') -可作四向手法

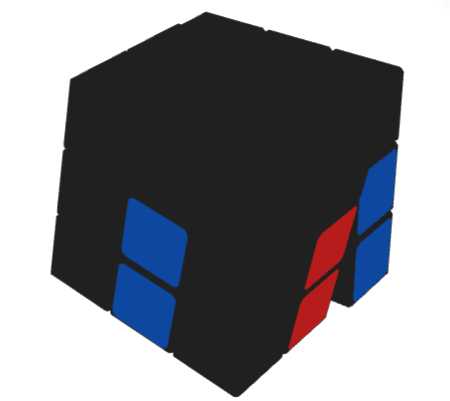
总结:R'避让，F上到层后R2即可组合插入。
情况V'：
y L F' L2' U L2 F L' -可作四向手法
y R' F R2 U R2' F' R -可作四向手法
(f R f') U (R U' R')
y2 (L' U' L) U (f' L f) -可作四向手法
y' (f' L' f) (R' U2' R) -可作四向手法

总结：通过f巧妙处理后转到U层插入。
情况V''：
R (L U2 L') R'
y L' (R' U2 R) L-可作四向手法

总结：Eazycase，到U层后直接插入。
情况V、V'、V''观察小结：很容易观察，只是识别之后快速反应需要加强。
原地翻棱，角块在邻槽：
情况W：
L F2' L' F U' F
(L F' L' U' F) U' (R U R')
y (L U' F' L' F) (L' U L)-可作四向手法

总结：藏角，运棱，组合，插入。
情况W'：
y R' F2 R F' U F' -可作四向手法
y (R' F R U F') U (L' U' L) -可作四向手法
(R' U F R F') (R U' R')

总结：藏棱，运角，组合插入。
情况X：
(R' F R U' F') (R U' R')
y (L' U' L) U (S' L' S) -可作四向手法

总结：藏棱，运角，组合，插入。
情况X'：
y (L F' L' U F) (L' U L) -可作四向手法
(R U R') U' (S R S')

总结：藏角，运棱，组合放入。
情况Y：
(L' U L) (M' U R U' r') (R U' R')
y (L U F' L' F) U2 (L' U' L) -可作四向手法
y (L U L') (F U F') U' (L' U L) -可作四向手法

总结：调整角块，调整棱块，组合，插入。
情况Y'：
y (R U' R') (M' U' L' U l) (L' U L) -可作四向手法
(R' U' F R F') U2 (R U R')
(R' U' R) (F' U' F) U (R U' R')

总结：调整角块，起棱，转化为简单F2L处理。
情况W/X/Y及其相对应镜像W'/X'/Y'观察小结：3组共计6种CASE，对比记忆与区别。
其他简单情况：
情况Z：
(R' F R U' F') U (R U' R')
R U' R2' u' R' u R
y2 L U' L2' u' L' u L -可作四向手法

总结：藏角，行棱，组合，插入。
情况Z'：
y (L F' L' U F) U' (L' U L)
y L' U L2 u L u' L' -可作四向手法
y' R' U R2 u R u' R'-可作四向手法

总结：藏角，行棱，组合插入。
情况Z及Z'观察小结：目标角块在位方向不对，目标棱块在侧与中心块色不相连。
全文总结：
以上共包含53种CASE的不同解法，还是以一首打油诗来总结一下：
非标之标不要怕，找准情况转化之；
藏角行棱，藏棱行角，有先后；
巧妙拆解，组合去，插入目标位置心不慌；
要问怎么强，努力练习是王道。
本文收录于我的知乎专栏：
三阶魔方-CFOP完全手册《飞旋马赛克》 - 知乎 (zhihu.com)
相关其他F2L教程还包括：
三阶魔方还原之CFOP-F2L从入门到精通 - 知乎 (zhihu.com)
三阶魔方CFOP进阶-空槽F2L - 知乎 (zhihu.com)
三阶魔方CFOP进阶-F2L 三色原理判断法-F2L提速小技巧 - 知乎 (zhihu.com)
三阶魔方CFOP进阶-标准F2L简单变化情况-FR部分 - 知乎 (zhihu.com)
三阶魔方CFOP进阶-标准F2L简单变化情况-FL部分 - 知乎 (zhihu.com)
其中还有两段式OLL，OLL双向，PLL双向及PLL观察法的教程，目前共计11篇内容。
欢迎关注，获取更多更专业的一手CFOP教学。
非标F2L图片如下，请自取：

——END——

可以的，用这个技能就可以。高斯还原 (コスモリダクション/Cosmo Reduction）
高斯奥特曼对自己身体的大小变化能力，能从微观到与人类等身，再巨大化至47米的原本体型。此技能也可转化为能作用于任意对象身上的巨大化·缩小化光线，将被缩小化/巨大化的人类或物体恢复原本的大小。
第17话中，高斯便以此能力把被异次元人吉吉缩小的SRC工作人员恢复原本大小；[15]
第44话中再度击败了异次元人吉吉后，高斯再次施展此技能，将巨大化至48米的超级高科技机器人克莱巴贡变回原本的半米左右大小
这个都能随便改物体的大小，复原个魔方很容易吧

[收藏本文] 【下载本文】

自然科学最新文章

海南一村民被眼镜王蛇咬死，多名消防员和村

有哪些不起眼的牢底坐穿兽？

美国耕地面积比中国大，可为什么粮食产量不

如何看待同济大学2024国家科技三大奖颗粒无

加:2024-01-06 21:31:15 更:2024-01-07 10:58:45

股票涨跌实时统计涨停板选股分时图选股跌停板选股 K线图选股成交量选股均线选股趋势线选股筹码理论波浪理论缠论 MACD指标 KDJ指标 BOLL指标 RSI指标炒股基础知识炒股故事

网站联系: qq:121756557 email:121756557@qq.com 天天财汇