| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 科技知识 -> 清华大学陈一镭发表量子算法,有望解决世界级算法难题「格密码」,该项工作有怎样的前景和意义? -> 正文阅读 |
|
|
[科技知识]清华大学陈一镭发表量子算法,有望解决世界级算法难题「格密码」,该项工作有怎样的前景和意义? |
| [收藏本文] 【下载本文】 |
|
Quantum Algorithms for Lattice Problems 近日清华大学交叉信息研究院陈一镭助理教授在eprint上发布了重要论文… |
|
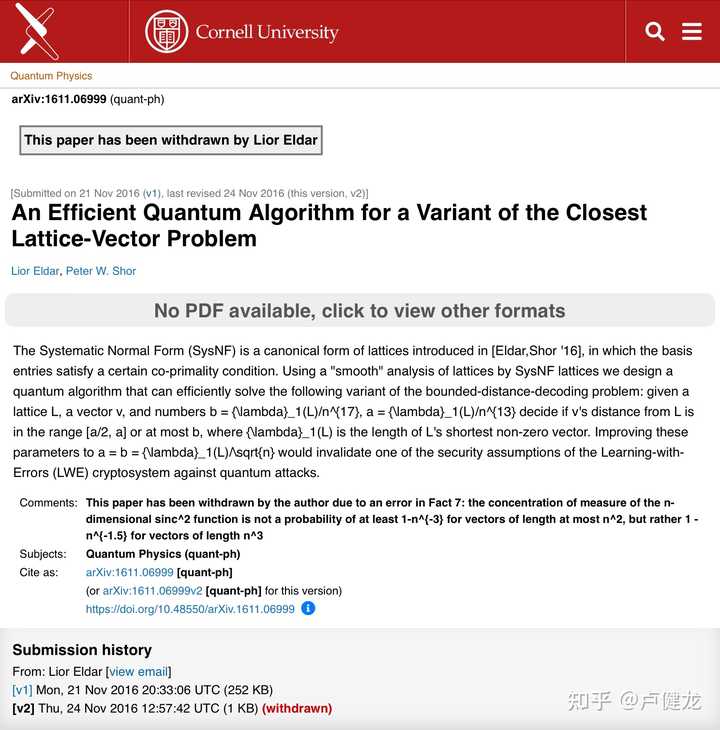
对于lattice problems这种众所周知的老大难问题,不是相关领域的人士最好还是不要轻易开香槟,特别是涉及到的还只是一篇未经同行评议过的预印本文章而已。即使是专业人士面对这些问题都很容易被打脸,例子太多了。 2016年11月21日的时候Lior Eldar和Peter W. Shor(就是著名的Shor算法名字里的那个Shor)就曾经在arXiv上放出过一篇预印本文章(“An Efficient Quantum Algorithm for a Variant of the Closest Lattice-Vector Problem”,arXiv:1611.06999(quant-ph)),在文章里两位作者声称已经找到了一种针对一类lattice problem的高效量子算法。但这篇文章很快被发现了有不可弥补的错误,两位作者也在短短三天后就从arXiv上自行撤稿了。 另外也有其他声称可以高效解决lattice problems的文章被放出来,但很多要么存在错误,要么被发现其实只能解决某些简化情况或者特殊情况(而且在这些情况中经典算法就已经足够了,并不需要额外的量子算法)。 非专业人士的围观对于这些还没定论的科研活动并没有太多促进作用,反而很容易给当事人增加一些没有必要甚至有害的压力。 |
|
|
|
|
占个坑,最近陈老师会给我们课题组过一遍文章中的细节,到时候或许能写一个比较详细的解读。 |
|
Lattice Problems 是一类与格结构相关的计算问题,在数论和密码学中很基础。 格是由一组线性独立向量生成的整数线性组合构成的所有点的集合。给定 (n)" role="presentation">(n) ( n ) 个线性独立向量 (b1,...,bn∈Rm)" role="presentation">(b1,...,bn∈Rm)( b_1, ..., b_n \in \mathbb{R}^m ) ,它们生成的格 (L(b1,...,bn))" role="presentation">(L(b1,...,bn))( L(b_1, ..., b_n) ) 包含所有形如 (∑i=1nxibi)的点,其中(xi∈Z)" role="presentation">的点,其中(∑i=1nxibi)的点,其中(xi∈Z) ( \sum_{i=1}^{n} x_ib_i ) 的点,其中 ( x_i \in \mathbb{Z} ) 。 Lattice Problems的一些困难包括: 最短向量问题(Shortest Vector Problem, SVP):在给定格的一个基的情况下,寻找该格中最短的非零向量。这个问题根据所采用的不同范数衡量最短线长的难度各异。通常考虑的是 (ℓp)" role="presentation">(?p) ( \ell_p ) 范数,其中 (1≤p≤∞)" role="presentation">(1≤p≤∞) ( 1 \leq p \leq \infty ) 。例如,在 (ℓ2)" role="presentation">(?2) ( \ell_2 ) 范数(二范数)下,目标是最小化向量的欧几里得长度。 最近向量问题(Closest Vector Problem, CVP):除了给定一个格以外,还给定一个目标点,目标是找到距离该目标点最近的格内的向量,并同样基于选定的 (ℓp)" role="presentation">(?p) ( \ell_p ) 范数来度量距离。 这些问题是 NP 完全的,并且对于任何常数因子的近似求解都非常困难。已知的算法提供了较大的近似比,如 LLL 算法可以将 SVP 在 (ℓ2)" role="presentation">(?2) ( \ell_2 ) 范数下以 (2n/2)" role="presentation">(2n/2) ( 2^{n/2} ) 的因子近似解决,虽然这个结果看似较差,但它在多项式因式分解、丢番图逼近、整数规划等领域有重大影响。更精确的确定性算法如 Schnorr 提出的算法可以达到 (2O(n(log⁡log⁡n)2/log⁡n))" role="presentation">(2O(n(log?log?n)2/log?n)) ( 2^{O(n(\log\log n)^2/\log n)} ) 的近似因子,而最优已知随机算法可以达到 (2O(nlog⁡log⁡n/log⁡n))" role="presentation">(2O(nlog?log?n/log?n))( 2^{O(n\log\log n/\log n)} ) 的因子。 对于 SVP 和 CVP 的精确解,所有已知算法的时间复杂度都是指数级的。对于 SVP,Kannan 提出的确定性算法运行时间为 (2O(nlog⁡n))" role="presentation">(2O(nlog?n)) ( 2^{O(n\log n)} ) ,而 Ajtai 等人给出的随机算法时间复杂度为 ( 2^{O(n)} )。 已知的结果表明,在任意 (1≤p≤∞)" role="presentation">(1≤p≤∞) ( 1 \leq p \leq \infty ) 的 (ℓp)" role="presentation">(?p)( \ell_p ) 范数下,CVP 至少需要 (nO(1/log⁡log⁡n))" role="presentation">(nO(1/log?log?n)) ( n^{O(1/\log\log n)} ) 的因子才能被近似求解。而对于 CVPP(带有预处理的最近向量问题),其难于在任何常数因子内进行近似,尤其是当 (p<∞)" role="presentation">(p<∞) ( p < \infty ) 时,其近似困难程度已被证明为 (5/3−ε)" role="presentation">(5/3?ε) ( \sqrt{5}/3 - \varepsilon ) ,并且后来这个界限进一步提高到了任何常数。 此外,还有其他相关的问题,如最短独立向量问题(Shortest Independent Vector Problem, SIVP)和最短基问题(Shortest Basis Problem, SBP)。这些问题也具有重要的理论意义和实际应用价值,尤其是在密码学中。 在格理论和密码学中,Approximate Shortest Vector Problem (ASVP) 是一个重要的计算问题,它要求找到给定格中长度接近最短的向量。具体来说,对于任意给定的正实数参数 δ,ASVP 要求找出格中长度不超过最短非零向量长度 δ 倍的向量。这个问题之所以重要,是因为其与一些基础数学问题紧密相关,并且在密码学中作为构建安全加密方案的基础难题。 解决 ASVP 通常非常困难,因为已知该问题在最坏情况下的确是 NP的,这意味着不存在多项式时间算法可以在所有情况下精确解决该问题。同时,即使允许一定误差范围内的近似解,找到足够好的近似解也至少在常数因子内保持 NP。已知的用于寻找确切解的算法的时间复杂度至少随格的维度以指数方式增长,这使得处理高维格时变得极其耗时。 陈提出了一种用于解决学习误差问题(Learning with Errors, LWE)的多项式时间量子算法,当LWE实例满足特定的模数噪声比条件时。结合Regev先前提出的从格问题到LWE问题的简化关系,这种算法进一步衍生出了多项式时间的量子算法,能够解决所有n维格上的决策性最短向量问题(GapSVP)和最短独立向量问题(SIVP),并且在逼近因子达到Ω\~(n^4.5)的程度上。在此之前,尚未发现能在任何多项式近似因子下解决所有格上的GapSVP或SIVP问题的多项式时间或次指数时间的量子算法。 为了开发这个解决LWE问题的量子算法,陈等人地引入了两种技术手段。一是使用具有复数方差的高斯函数构造量子算法,特别是利用复高斯函数离散傅里叶变换中的Karst波特性。二是采用带复高斯窗的窗口化量子傅里叶变换,这种方法能够整合来自时域和频域的信息,使得算法能够更有效地运作。 算法的基本流程:首先将LWE实例转化成具有纯虚部高斯振幅的量子态,接着将这些纯虚高斯状态转换为关于LWE密值和误差项的经典线性方程组,最后通过高斯消元法求解这个线性系统,从而在多项式时间内解决LWE问题。 这个研究的意义在于打破了对格问题如GapSVP和SIVP在通用情况下高效求解的理论壁垒。由于格问题的困难性是现代密码学中的关键,尤其是像全同态加密这样的高级加密方案构建的基础,而LWE更是被广泛应用于经典和量子计算领域的全同态加密体制之中,以及NIST后量子密码标准候选方案之一。此前认为量子计算机难以在多项式时间内破解这些问题,但本文的工作揭示了一种特定参数下的LWE及其相关格问题可在量子计算机上得到多项式时间复杂度的尝试。 论文详细描述了如何逐步逼近目标,即通过巧妙地利用复高斯函数性质获取部分坐标信息。例如,通过相位回踢技巧改变量子态的相位,然后执行量子傅里叶变换(QFT)得到一个关于模D2p1的线性方程,从而获取部分信息。随后利用LWE实例中预设的秘密向量中的p2,..., pκ值进一步获得有关v更多信息,最终提炼出关于LWE秘密和误差项的模线性方程。 在算法的具体步骤中,首先创建了在整数格子ZnDq上的叠加态,并应用复高斯窗引理,可以在多项式时间内生成一种特殊的量子态,其中包含了与格空间L及某个特定范围内的元素相关的权重。通过测量和后续操作,可以得到与L中某向量v以及y'之间的关系,从而进一步处理量子态并提取关于LWE问题中秘密变量和误差项的模线性方程。 此外,文章还深入讨论了特定量子子程序的技术细节,包括如何通过一系列复杂的变换和矩阵运算,将原始的LWE问题映射到一个易于处理的量子态表达式,然后通过对量子态的分析和分解,逐步解开隐藏在LWE实例中的秘密和误差信息。 这项工作的重要贡献在于它不仅提供了一种在量子计算机上高效解决LWE问题的新方法,而且也扩展到了其他与格问题密切相关的计算问题,如GapSVP和SIVP。这种进展不仅对密码学研究产生深远影响,因为它挑战了现有的基于格问题构建的密码系统的安全性假设,同时也推动了量子计算在密码破译、优化算法、以及实际物理世界中涉及格问题的各种场景中的应用潜力。 未来应用方面,此项研究的突破将潜在地影响到密码系统的安全性评估、公钥密码体制的设计与实现、以及数据安全存储和传输等领域。例如,可能促使密码学者重新审视基于LWE等格问题构建的安全协议,并发展出针对量子计算机更为稳健的安全加密技术。此外,由于格问题本身也是数学和计算几何领域的重要课题,新的量子算法也将有助于提升我们在结构化数据分析、优化问题求解等方面的能力。 |
|
如果是真的,意味着目前的大量的后量子密码学相关论文的价值变为了原来的1/1000。 题外话,这将会是对潘建伟老师的公司国盾量子有史以来最大的利好。 因为在原来,无论是长期还是短期,都认为只要使用上了后量子密码学,就不会被量子计算机攻破。从而密码学算法将不会是安全体系短板。 但是如果是真的话,那么后量子密码算法将不再安全,未来还是需要使用量子密码协商从物理机制上来保证密钥分发的安全性。 无疑这极大的扩展了国盾量子的市场面。 |
|
有点受不了上面有些答案了。先叠个buff,个人lattice的水平相当于本科生的水平,如果错误还轻大佬指出我好修正。 评价这个工作的意义可以有几方面角度: 首先,这篇文章不是第一个来question LWE hardness的文章,上面已经有哥们提到了。但是前面的文章要么有fundamental的错误要么过于简化问题了。但是纠结是不是第一个来做这个意义不大,第一个作出有意义的结果意义比较大。 其次,假设整篇文章的提供了一个sound的结果。是不是意味着lattice base cryptograph无了? 这一点感觉还不是很清晰。文章作者也提到了,即使这个结果正确也不意味着现在的这些lattice proposal直接无了。但是,攻击在多数情况下都是可以被改进的,甚至数学证明也是可以被改进的。正面例子如张益唐证明相邻素数间隔有限的文章,文章已经发出验证后很快bound就从几千万被改进到几千了(如果我记得没错)。另一个正面例子是王小云院士的hash collision工作,也被后面的人在2017年改进到能实际进行攻击了。 进一步,如果这篇工作导致lattice base cryptography无了,是不是直接利好量子加密(个人不是很懂什么是量子加密)? 个人觉得这个问题答案是否定的,先不说什么美国政府已经有报告说量子密钥分发实际意义不大以及种种阴谋论。要我说NIST那帮人还是有两把刷子的,可能以前就吃过亏。我记得NIST explictly说到过最终的post-quantum candidates一定要一个非lattice based,这样押宝不押一个免得到时候出问题了手忙脚乱。所以,post-quantum的方案不仅仅是lattice-based,还有其他五六种可供选择的困难问题,比较promising的也还有两三个。所以未来即使lattice base cryptography无了,也还有其他问题可以用来构造post-quantum的算法。 再次,在文章正确的前提下,怎么看待这篇的科学贡献? 首先,什么CRYPTO/EUROCRYPT,FOCS/STOC最佳论文 test-of-time预定一波。可供参考的是去年EUROCRPYT上攻击SIKE的团建,毫无疑问的直接拿下了best paper。但是上述这些论文能不能够的上test-of-time我还持怀疑态度。这篇可能预定15年后的test-of-time的关键是它的target是困难性问题,而上述SIKE的攻击只是针对的特定构造方案。一个不是很恰当的比喻是困难性问题如同给出了二氧化碳+糖水的组合是万千肥宅的快乐水,特定构造方案就相当于你来调个可乐我来调个雪碧,他来加点果汁弄个芬达。一个更直观的说法可能是,这篇文章可以使得近来几乎所有的post-quantum的炼丹成为一炉废丹,而前面去年的SIKE攻击paper只是说有一粒丹(SIKE)是废丹,二其他丹(基于isogeny)可能还是好的。 最后,这篇论文能得图灵奖吗? 个人感觉几乎不可能,虽然基于朴素的民族情绪我也希望能。本质上说,整篇文章的可能贡献就是证明lattice的喜闻乐见的难题LWE不能再被认为是困难的了。同等贡献的有Peter Shor证明大数分解不那么安全,并且他还有第一个用量子计算来研究密码学的困难性问题的buff。所以即便颁奖也应该给他。还有,整篇文章并不能够全盘否定lattice based cryptography(在我看来),LWE等问题解决应该不能直接证明SIS及其变种解决,虽然SIS能玩的花样很少并且整个lattice的安全会受到质疑。另外个人觉得同等地位的工作还是有不少的,比如Coppersmith,LLL reduction,Paul Kosher的side channel。 修正1:根据https://web.eecs.umich.edu/~cpeikert/pubs/slides-abit2.pdf 46/94, LWE可以在有quantum 的条件下reduct TO SIS. 因此quantum的LWE快速算法能够攻击SIS。(这一点欢迎大家来指正) 修正2: 是其他基于isogeny的protocol不是SIDH. |
|
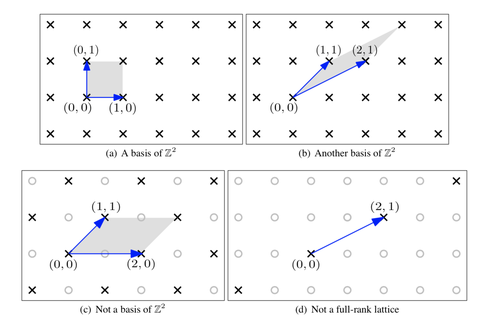
密码学和量子算法都是非常抽象和技术性的领域,这里只简单介绍一下基本的概念,以解释这项研究的意义。 容错学习问题是由Oded Regev于2005年在一篇题为On Lattices, Learning with Errors, Random Linear Codes, and Cryptography(关于格,容错学习,随机线性码和密码学)的论文中提出的。Regev在论文中证明了,这个问题和几个最坏情况的格问题一样难,例如GapSVP(判定性最短向量问题)和SIVP(最短线性独立向量问题),格就是离散的格点,对格问题的介绍可以看下面这个回答: 如何看待 Oded Regev 荣获 2018 年哥德尔奖?86 赞同 · 3 评论回答 |
|
|
什么是容错学习问题?其实就是求解带误差的线性方程组: ⟨s,a1⟩≈ϵb1 (mod 2)⟨s,a2⟩≈ϵb2 (mod 2)⋯" role="presentation">?s,a1?≈?b1 (mod 2)?s,a2?≈?b2 (mod 2)?\begin{aligned} \langle \mathbf{s},\mathbf{a}_1\rangle &\approx_\epsilon b_1 \ (\text{mod } 2)\\ \langle \mathbf{s},\mathbf{a}_2\rangle &\approx_\epsilon b_2 \ (\text{mod } 2)\\ &\cdots \end{aligned} 其中, ai" role="presentation">ai\mathbf{a}_i 是从 Z2n" role="presentation">Z2n\mathbb{Z}_2^n 上的均匀分布中独立随机选取的。注意,这个方程组中出现的是约等号,而不是平常的等号,每个方程独立正确的概率是 1−ϵ" role="presentation">1??1-\epsilon 。问题的目标是解出 s" role="presentation">s\mathbf{s} 。在 ϵ=0" role="presentation">?=0\epsilon=0 时,就是平常的线性方程组,有Gauss消元这个熟悉的高效求解算法,可以在 poly(n)" role="presentation">poly(n)\text{poly}(n) 时间求解。但在 0">ϵ>0" role="presentation">?>0\epsilon>0 时,如果只是简单地推广Gauss消元,在 2O(n)" role="presentation">2O(n)2^{O(n)} 时间内才能求解,问题的复杂度迅速上升。 借助这篇只是引入并证明容错学习问题有多么难的论文,Oded Regev就获得了2018年的G?del奖,这个奖表彰在理论计算机科学领域取得开创性贡献的研究者。问题中这项研究声称,提出了在 poly(n)" role="presentation">poly(n)\text{poly}(n) 时间内求解容错学习问题的量子算法。如果这项研究中的证明准确无误,那无疑也是理论计算机科学领域的开创性贡献。 |
|
谢邀@ Harogenshi。 我现在暂时没时间写详细内容,先大概翻译一下这篇论文的摘要部分,等会儿再补充(机翻的,可能不大准确,先凑合着看看)。 “我们给出了一种求解具有一定多项式模噪声比的带误差学习问题的多项式时间量子算法。结合Regev[J.ACM 2009]所示的从格问题到LWE的约简,我们获得了在近似因子2(n4.5)内求解所有n维格的决策最短向量问题(GapSVP)和最短独立向量问题(SIVP)的多项式时间量子算法。以前,对于任何多项式近似因子内的所有晶格,没有已知的多项式甚至次指数时间量子算法来求解GapSVP或SIVP。 为了开发求解LWE的量子算法,我们主要引入了两种新技术。首先,我们在量子算法的设计中引入了具有复方差的高斯函数。特别地,我们在复高斯函数的离散傅立叶变换中利用了岩溶波的特征。其次,我们使用具有复高斯窗口的窗口量子傅立叶变换,这使我们能够组合来自时域和频域的信息。使用这些技术,我们首先将LWE实例转换为具有纯虚高斯振幅的量子态,然后将纯虚高斯态转换为LWE秘密项和误差项上的经典线性方程,最后使用高斯消去法求解线性方程组。这就给出了求解LWE的时间量子算法。” |

|
|
等会儿回寝室再写~ 首先什么是格和格问题。对于 n" role="presentation">nn 维欧氏空间 Rn" role="presentation">Rn\mathbb R^n 及其一组基 B={b1,b2,⋯,bn}" role="presentation">B={b1,b2,?,bn}\boldsymbol{ B}=\{\boldsymbol{b}_1,\boldsymbol{b}_2,\cdots,\boldsymbol{b}_n\} ,我们定义离散子群 L(\boldsymbol{ B})=\{\displaystyle\sum_{i=1}^nx_i\boldsymbol{b}_i:x_i\in\mathbb Z\} 是由 B" role="presentation">B\boldsymbol{B} 生成的一个格。SVP(最短向量问题)包括一系列寻找满足 ‖x0‖=λ1(L)=minx∈L−{0}‖x‖" role="presentation">‖x0‖=λ1(L)=minx∈L?{0}‖x‖\| \boldsymbol x_0\|=\lambda_1(L)=\displaystyle\min_{ \boldsymbol x\in L-\{ \boldsymbol 0\}}\| \boldsymbol x\| 的向量 x0" role="presentation">x0 \boldsymbol x _0 的问题,例如近似最短向量问题(Approximate SVP)、间隙最短向量问题(GapSVP)和最短独立向量问题(SIVP),其中近似最短向量问题表述如下: 给定一组基 B" role="presentation">B\boldsymbol B ,寻找一个非零向量 x∈Zn" role="presentation">x∈Zn\boldsymbol x\in \mathbb Z^n 使得 ‖Bx‖≤γ(n)λ1(L)" role="presentation">‖Bx‖≤γ(n)λ1(L)\|\boldsymbol {Bx}\|\le\gamma(n)\lambda_1(L) ,其中 γ(n)" role="presentation">γ(n)\gamma(n) 是近似因子。 这篇论文的主要结果在于使用多项式时间量子算法解决了特定模数噪声比下的LWE,即带错误学习问题,这与SVP是等价的: 对任意 m,n,q∈N" role="presentation">m,n,q∈Nm,n,q\in\mathbb N 及 α∈(0,1)" role="presentation">α∈(0,1)\alpha\in (0,1) 使得 m≥Ω(nlog⁡q)" role="presentation">m≥Ω(nlog?q)m\ge \Omega (n\log q) , q∈Ω∼((αq)4m2)" role="presentation">q∈Ω~((αq)4m2)q\in \overset{\sim}{\Omega} ((\alpha q)^4m^2) ,存在一个量子算法在多项式时间 poly(m,log⁡q,αq)" role="presentation">poly(m,log?q,αq){\rm poly}(m,\log q,\alpha q) 内解决 LWEn,m,q,U(Zq),DZ,αq{\rm LWE}_{n,m,q,U(\mathbb Z_q),D_{\mathbb Z,\alpha q}} 。 有时间再接着写。 |
|
如果为真,这篇论文有可能是中国有史以来对密码学届最重要的贡献(也许不需要之一),姚期智的多方安全计算发表单位不能算中国的吧... 这简直是对我的打脸现场,前几天刚写了一个唱衰量子通信的回答。 我唱衰量子通信最主要的原因是:我们有几乎0成本的软件抗量子密码算法。如果这个基础不存在,那么就还不能完全否定量子通信的价值。 不过,其他唱衰理由仍然成立。 |
|
强答一下下。。。 清华大学陈一镭的主要内容是展示了一个用于解决具有特定多项式模数-噪声比的带错误学习问题(Learning with Errors,LWE)的多项式时间量子算法[1]。 在开发这一算法的过程中,清华大学陈一镭组引入了两种新技术:首先是在量子算法的设计中引入了具有复数方差的高斯函数,从而利用了复高斯函数的离散傅里叶变换中的Karst波特性。其次,使用带有复高斯窗口的窗口化量子傅里叶变换,这使我们能够结合时间和频率域的信息。 通过上述两种新技术,陈组首先将LWE实例转换为具有纯虚高斯振幅的量子态,然后将纯虚高斯量子态再转换为关于LWE秘密和误差项的经典线性方程,最后使用高斯消元法解决线性方程组,从而得到了可以解决LWE的多项式时间量子算法。 根据Regev在09年的工作中展示的将最坏情况下的格问题,如决策性最短向量问题(GapSVP)和最短独立向量问题(SIVP),和LWE的之间的等价转化关系[2],本工作如果获得验证,就意味在获得了适用于所有『格问题』并且复杂度在?(n^4.5)的多项式时间量子算法。而在此之前,对于GapSVP或SIVP问题都没有找到多项式或甚至指数时间量子算法。 参考^https://eprint.iacr.org/2024/555^Regev O. On lattices, learning with errors, random linear codes, and cryptography[J]. Journal of the ACM (JACM), 2009, 56(6): 1-40. |
|
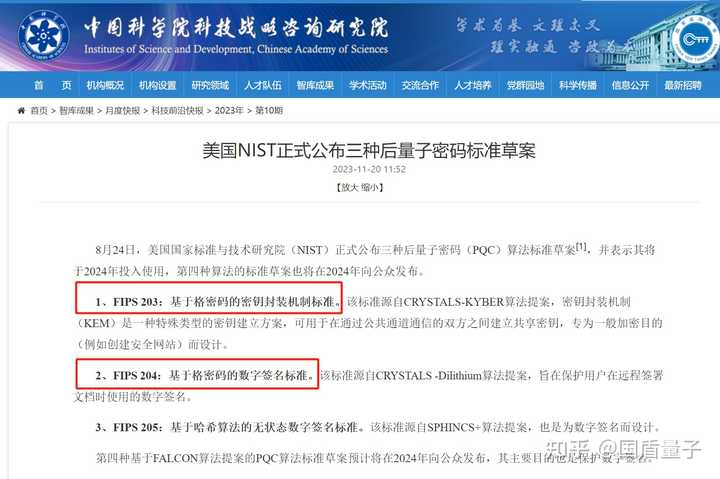
忽然被cue,来了来了~~~这个成果还处于同行评议中啦,还是先蹲一下后续的进展。如果通过了评审,那这一工作的意义如上所述,一方面,对于量子计算而言,是继大数分解后,量子算法上的重要突破。另一方面,就应对量子计算对经典密码威胁的举措而言,会对美国NIST过去10年来选择后量子密码设计的思路产生颠覆性的影响,去年美国国家标准与技术研究院公布的三种后量子密码(PQC)算法标准草案,有两种都是基于格密码,而这一成果让其安全性再受质疑。量子计算的“矛”越来越锋利,而PQC铸成的“盾”似乎有些不靠谱了。 |
|
|
“以经典抗量子——后量子密码算法(PQC)”和“以量子抗量子——量子密码技术”,是当前抵御量子计算对经典密码破解威胁、实现信息安全机制的两种主要途径。 问题中的格密码便是极具代表性的PQC。PQC基于已知量子算法无法多项式时间求解的数学困难问题而设计,安全性依赖于计算复杂度。但未来PQC依赖的数学难题是否依然难解、算法安全性是否长期有效、面对新出现的量子攻击是否依旧免疫等问题,都是未知的。此次破解格密码量子算法的研究也表明,PQC存在一定脆弱性和不确定性因素。 所以相比较而言,具有长效安全性的量子密码是一劳永逸的解决方案。 量子密码的显著优势在于,基于自身量子物理实现原理,即单量子不可分割、量子态不可克隆所实现的抗量子计算攻击能力。以其中最具代表和实用性的量子密钥分发技术为例,通信双方通过传送量子态的方法,实现信息论安全的密钥生成和分发的方法和过程,即使在攻击者拥有无限强的计算资源下也仍然安全。 |
|
|
| [收藏本文] 【下载本文】 |
| 科技知识 最新文章 |
| 百度为什么越来越垃圾了? |
| 百度为什么越来越垃圾了? |
| 为什么程序员总是发现不了自己的Bug? |
| 出现在抖音评论区里边的算命真不真? |
| 你认为 C++ 最不应该存在的特性是什么? |
| 为什么 Windows 的兼容性这么强大,到底用了 |
| 如何看待Nvidia禁止使用翻译工具将cuda运行 |
| 为何苹果搞了十年的汽车还是难产,小米很快 |
| 该不该和AI说谢谢? |
| 为什么突破性的技术总是最先发生在西方? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |