| |
| 首页 淘股吧 股票涨跌实时统计 涨停板选股 股票入门 股票书籍 股票问答 分时图选股 跌停板选股 K线图选股 成交量选股 [平安银行] |
| 股市论谈 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 商业财经 科技知识 汽车百科 工程技术 自然科学 家居生活 设计艺术 财经视频 游戏-- |
| 天天财汇 -> 科技知识 -> 为什么深度学习中神经元不是y=kx2+b加一个激活函数呢? -> 正文阅读 |
|
|
[科技知识]为什么深度学习中神经元不是y=kx2+b加一个激活函数呢? |
| [收藏本文] 【下载本文】 |
|
现在的深度学习每个神经元中几乎都是y=kx+b加激活函数,为什么不试着提高一下x的次方呢? |
|
很好的问题,事实上,有一个很小的领域叫做Quadratic Neural Networks。专门就是研究题主所说的这一类神经网络。鄙人不才,恰好对这个小领域有一点研究,在此做一点介绍。这一方向的相关学者主要有Fenglei Fan(CUHK,二次神经网络理论),Zirui Xu(CVS Health,二次神经网络计算),Grigorios G Chrysos(UW–Madison,高次神经网络理论),我也在这个领域做了一些极其微小的贡献。 1. 万能近似定理(Universal Approximation) 事实上,由多次神经网络的万能近似定理[1], 一个由简单神经元 y=ax+b" role="presentation">y=ax+by=ax+b 经过我们常用的激活函数后,就可以形成对任意函数的任意精度的拟合。也就是说,数据的高次关系在神经网络的优化过程中是可以被拟合的,这是目前绝大多数神经网络采用了简单的神经元的主要原因。 然而,一个没有引入任何prior knowledge的神经网络一定是最好的吗?高次关系在优化过程中面临的问题是,我们通过SGD所得到的optimal不一定反映这样的高次关系,网络的可解释性在这里也遇到了一定问题。所以与其用NN完全构建一个黑盒,我们不如在其中主动构建一些prior,主动在网络结构/计算中引入高次关系。 2. 高次神经网络 Quadratic NNs在于挖掘数据自身的二次关系到目标(以及网络中间状态)的mapping。但是,实际上挖掘数据自身的高次项在神经网络中的作用已经有了非常多的相关工作,我们归纳一下,在CV的backbone neural network中主要有以下几种形式: (1)注意力机制(Attention):利用数据本身构建一个input adaptive weight,然后这个机制的输出通常是 y=Att(X)×Wx" role="presentation">y=Att(X)×Wxy = Att(X) \times Wx 。代表有ViT,Attention CNN等等 (2)双线性池化(Bilinear-Pooling): 在池化层引入高次关系。 (3)二次神经网络(Quadratic Neural Networks): y=XTAX+WX+b" role="presentation">y=XTAX+WX+by = X^TAX+WX+b (4)多项式神经网络(Polynomial Neural Networks): y=∑i=0nkiXi" role="presentation">y=∑i=0nkiXiy =\sum_{i=0}^{n} k_iX^i。代表有P-nets等。 对此,我略微整理了一个github repo: https://github.com/miniHuiHui/awesome-high-order-neural-network?github.com/miniHuiHui/awesome-high-order-neural-network 里面列举了每一类的代表作。 3. 二次神经网络 我在一篇paper中提出了QuadraNet, 这篇文章叙述了二次神经网络在计算上相对于其它高次神经网络的优势,以及其所提供的新的网络搜索空间对于Neural Architecture Search的影响。这篇文章获得了ASP-DAC 2024 的Best Paper Nomination. 首先,如下图,二次神经元具有更强的representation capacity是毋庸置疑的。 |

|
|
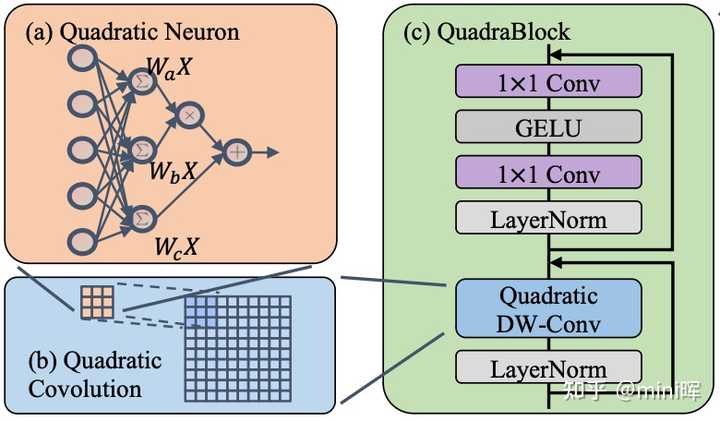
接着我们证明了现在最主流的网络ViT的本质是一个三次神经网络, 因为Self-attention的计算可以被写为ySelf−Attention(i,c)=∑j∈Ωi∑c′=1CA(x)i→jTV(c′,c)x(j,c′)," role="presentation">ySelf?Attention(i,c)=∑j∈Ωi∑c′=1CA(x)i→jTV(c′,c)x(j,c′),y_{Self-Attention}^{(i,c)} = \sum_{j \in \Omega_i}\sum_{c'=1}^CA(x)_{i\rightarrow j}T_V^{(c',c)}x^{(j,c')}, 其中 A(x)" role="presentation">A(x)A(x) 由Q,K相乘而来,而Q,K本质都是输入x的一个线性变换。 将这一个过程简化,可以用一个更深的二次神经元构建的卷积来替代Swin Transformer中的Self- Attention,这是因为Self-Attention的本质是挖掘pixel间的spatial上的高次关系。而用一个融合了二次神经元的depth-width convolution同样可以在线性复杂度下做到一个高次关系提取。这么做可以在相同的计算规模下增加网络深度,提升FFN层的计算密度,这样可以做到更多的信息encoding。 |
|
|
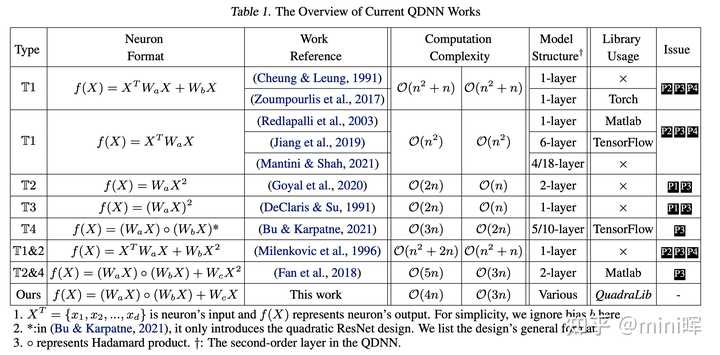
QuadraNet的基本结构4. 二次神经网络的计算和加速 我们组先前的一篇工作QuadraLib提供了一个Quadratic Neural Networks的计算库,对各种各样的二次神经网络做了分类,并对其计算复杂度,计算特征做了相应的分析。这篇文章获得了MLSys 2022 的Outstanding Paper Award。 |
|
|
这篇文章中还首次提出了对二次神经元中的二次项做一个类似LoRa的分解,以达到最优的计算复杂度和模型性能的Tradeoff。如果对二次神经网络的计算感兴趣,可以详细读一下这篇文章。 Reference: [1] Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators[J]. Neural networks, 1989, 2(5): 359-366. [2] Xu, C., Yu, F., Xu, Z., Liu, C., Xiong, J., & Chen, X. (2023). QuadraNet: Improving High-Order Neural Interaction Efficiency with Hardware-Aware Quadratic Neural Networks.arXiv preprint arXiv:2311.17956. (ASP-DAC 2024 Best Paper Nomination) [3] Xu, Z., Yu, F., Xiong, J., & Chen, X. (2022). Quadralib: A performant quadratic neural network library for architecture optimization and design exploration.Proceedings of Machine Learning and Systems,4, 503-514. |
|
当时是可以的, kx2+b" role="presentation">kx2+bkx^2+b 可以看作是Gated Linear Unit的特殊情况。 一般形式的GLU为, GLU(x)=f(x)⋅σ(g(x))" role="presentation">GLU(x)=f(x)?σ(g(x))GLU(x)=f(x) \cdot \sigma(g(x)) ,其中 f" role="presentation">ff 和 g" role="presentation">gg 是linear transformation, σ" role="presentation">σ\sigma 一般为非线性激活。 如果我们将 σ" role="presentation">σ\sigma 简化,变为identity,则这个GLU则可以变为 f(x)⋅g(x)" role="presentation">f(x)?g(x)f(x) \cdot g(x) ,再化简就可以近似得到 一个关于 x" role="presentation">xx 的二次形式。 同时,这个简化的GLU本身因为本身就包含非线性了,因此可以看做是一类带激活的transformation。 Simple Baselines for Image Restoration?arxiv.org/abs/2204.04676 之前一篇关于图像复原的模型设计论文就是类似的思路,常用的GELU可以看做是GLU的特殊形式,再将GLU化简,得到SimpleGate。 当然这个形式还可以继续拓展将其看作一类attention,如果 x" role="presentation">xx 是来自于不同scale的,即 y=k⋅x1⋅x2+b" role="presentation">y=k?x1?x2+by=k \cdot x_1 \cdot x_2 +b ,则可以看做是跨scale间的attention的一种形式,具体可以参考上面这篇论文中SimpleGate的下一小节,Simplified Channel Attention。 类似的还有下面这篇论文中的Multiplication based Channel Attention。 CVPR 2021 Open Access Repository?openaccess.thecvf.com/content/CVPR2021/html/Wei_Shallow_Feature_Matters_for_Weakly_Supervised_Object_Localization_CVPR_2021_paper.html |

|
|
|
|
不太认同楼上GLU那个观点,GLU是做两个linear transform再相乘,kx2是同一个linear transform乘两次,没引入新的信息量。而且x平方反而限制了每个维度都是正数,不如直接学x表现能力强。 |
|
为什么深度学习中神经元的基本形式倾向于使用线性函数y=kx+b再加上激活函数,而不是采用更高次方的形式,如y=kx2+b加激活函数? 简单的说,简单就是美。如果能用越简单的表示能够获得同样性能,为什么要复杂化呢。比如ReLU激活函数很简单,但同样很实用,也广泛应用到深度学习。 当然,如果要学究式探讨,我们可以从多方面进行,包括设计原则、计算复杂性以及模型泛化能力等方面的因素。核心是深度学习模型的设计旨在找到一个既能有效捕捉数据复杂性又能维持计算可行性和良好泛化的平衡点。 从模型的表达能力角度出发,理论上,包含至少一个隐藏层且具有足够多神经元的深度神经网络,使用简单的线性映射加非线性激活函数已被证明可以逼近任何复杂的函数,这是基于通用近似定理的结论。线性映射y=kx+b是最简单的形式,但当它通过激活函数和多层网络的组合,网络能学习到更为复杂的非线性关系。换言之,即使是基于简单线性映射的神经元模型,在多层结构中也能够表达非常复杂的函数。 考虑到计算效率,y=kx2+b的形式引入了更高的计算复杂性。在深度学习训练过程中,优化算法(如梯度下降法)需要计算损失函数关于模型参数的梯度。当引入x的高次项时,梯度计算会变得更加复杂和计算量更大。这不仅增加了单次迭代的计算成本,还可能影响模型的收敛速度和稳定性。在实践中,为了使模型训练在合理的时间内完成,并保持较好的性能,保持模型的计算效率是非常重要的。 从模型泛化能力的角度考虑,使用更高次方的模型可能导致过拟合问题。过拟合是指模型在训练数据上表现良好,但在未见过的数据上表现较差。引入x的高次项意味着模型变得更复杂,更容易捕捉到训练数据中的噪声,而不是其背后的真实关系,这样会降低模型在新数据上的预测能力。因此,在模型设计时需要权衡模型的复杂度和泛化能力。 实践中的可行性和需求也是一个重要因素。虽然在理论上探索不同形式的神经元是可能的,但在大多数实际应用中,简单的线性映射加上非线性激活函数已经能够提供良好的性能。此外,深度学习社区中的研究和实践已经积累了大量关于这种模型的经验和技术,包括如何有效训练模型、避免过拟合等。这种丰富的知识库为使用标准形式的神经元提供了强大的支持。 尽管目前的神经网络架构大多采用线性映射加非线性激活函数的设计,但科学研究的本质是不断探索和尝试。实际上,有研究在探索使用不同类型的神经元和激活函数,包括多项式神经元、径向基函数(RBF)神经元等,以适应特定的应用需求或提高模型性能。这些尝试在某些特定情况下可能会带来性能的提升,但也伴随着上述提到的挑战。 |

|
|
|

|
|
|

|
|
|

|
|
|
|
因为麻烦,谁知道是几次方的关系,还不如多堆几层,靠参数和非线性拟合数据。而且平方立方的,动不动就爆成NaN了。 |
|
没有看过相关的文献,但是有一些直观的感受。首先,毋庸置疑y=kx+b是一个线性映射。那么线性组合在一个模型中一般会起到什么作用呢?我认为是加权组合。我想如果你要用一种更可能符合凸性的方式去组合加权,唯有使用这种线性组合。当然你可能会问为什么要满足凸性,因为一旦函数符合凸性,我们就可以更容易地找到最优点。其次,大家都知道神经网络是非线性映射,那么这种非线性可以是任意的非线性吗?打个比方,非线性的激活函数就有很多,但是事实就是,即使只是在激活函数层面施加不同的非线性,整个网络都很可能走向不可控不收敛。我打个简单的比方,你能直接用x的0.5次方来激活吗?如果你要在激活函数之前引入更加复杂的非线性,那么要达到更加优化的结果就会更困难,因为复杂的函数客观上就是更难收敛。所以这其实是设计层面的简单想法,无论当前有没有人在做这个,凸性和非线性的调控我认为都是必须考虑的。 再者就是其他楼主所提到的表现力问题,如果使用了二次的映射,反而会对于一些值域有所忽略,因为梯度图一定会发生很大的变化,而且因为函数阶次升高会更加多变。这个时候神经网络所应用的优化算法如果跟不上,那就更容易陷入局部最优点。 |
|
那为什么咱们春节回老家是直接回去,而不是先坐飞机到美国绕一圈再到老家呢? |
|
如果是平方,没办法区分输入是正还是负数。感觉不太合理呀。 要是立方感觉还可以。难道可以省去激活函数么?也可以做做实验。 不过这样值域范围有点大,不知道会不会很难收敛? 直觉上感觉立方就是把输入放大,然后接下一层放的更大。。。。估计应该效果会变差。。。。或者很难学会 |
|
因为低效且开销大 |
|
因为一次函数是最基础的基函数 通过多次relu 可以变为非线性 你说的这种可以降低计算开销 少叠加几次 |
|
深度学习里的神经元就像是一个简单的计算器,它先把输入的数据(x)乘以一个数(k),再加上一个数(b),然后再通过一个激活函数来处理结果。这样做可以让模型更好地适应各种复杂的数据。 你提到的提高x的次方,就像是让这个计算器可以做乘法或者更高阶的运算。确实,这可以让模型变得更复杂,处理更复杂的数据。但在深度学习中,通常会用其他更高级的方法来达到这个效果,比如添加更多的计算层或者使用更复杂的激活函数。这是因为这些方法已经被证明在很多任务上都表现得很好。 |
|
线性可以简化计算, 所以做算法时倾向于使用线性, 而且深度学习本质上是分类,比如训练一个小狗模型。 假如有个黑板,小狗的照片贴在左边,不是小狗的照片贴在右边,中间划一条直线就可以实现。所以就画直线。如果加个小猫一起分类的话,再画一条直线。 如果画二次曲线,等做成矩阵,一层又一层迭代,就搞超级复杂了。 ps1: 加上显卡特别适合算矩阵乘法。阵列的y=kx ps2:工作之后发现大部分工程问题都会简化成线性。 个人看法,不一定对。 |
|
楼上很对,在不限制神经元数目的情况下本质一样,表达能力不增不减 |
|
可以但麻烦 |
|
因为如果激活函数是y=x^2,跟这个问题是等价的 |
|
非线性通常不是不愿意,而是涉及复杂度难点。 |
|
如无必要,____ |
|
这是深度学习产生作用的最重要根源,提供了非线性。理论上,只要是有足够多的非线性,就可以拟合任何的数学曲线(经过合理的训练),日常的问题,包括检测、分类等,也包括复杂度更高的大模型,也是可以看作是一系列的数学曲线,然后更大规模的非线性模型来拟合这个这些日常问题的数学曲线。 |
|
可能因为两次一次函数就能建模一个二次函数?也就是两层一次的网络就可以模拟一层二次的网络了。但是二次元网络没法模拟一个三次的网络啊。 换个说法,这和所有自然数都可以用1+1+...拼起来一样,但是奇数是不能被2拼起来的。 |
|
|
| [收藏本文] 【下载本文】 |
| 科技知识 最新文章 |
| 百度为什么越来越垃圾了? |
| 百度为什么越来越垃圾了? |
| 为什么程序员总是发现不了自己的Bug? |
| 出现在抖音评论区里边的算命真不真? |
| 你认为 C++ 最不应该存在的特性是什么? |
| 为什么 Windows 的兼容性这么强大,到底用了 |
| 如何看待Nvidia禁止使用翻译工具将cuda运行 |
| 为何苹果搞了十年的汽车还是难产,小米很快 |
| 该不该和AI说谢谢? |
| 为什么突破性的技术总是最先发生在西方? |
| 上一篇文章 下一篇文章 查看所有文章 |
|
|
|
| 股票涨跌实时统计 涨停板选股 分时图选股 跌停板选股 K线图选股 成交量选股 均线选股 趋势线选股 筹码理论 波浪理论 缠论 MACD指标 KDJ指标 BOLL指标 RSI指标 炒股基础知识 炒股故事 |
| 网站联系: qq:121756557 email:121756557@qq.com 天天财汇 |